Моноклинная кристаллическая система - Monoclinic crystal system


В кристаллография, то моноклинная кристаллическая система один из семи кристаллические системы. Кристаллическая система описывается тремя векторов. В моноклинной системе кристалл описывается векторами неравной длины, как в ромбический система. Они образуют прямоугольную призма с параллелограмм в качестве его основы. Следовательно, две пары векторов перпендикулярны (встречаются под прямым углом), а третья пара образует угол, отличный от 90 °.
Решетки Браве
Двумерный
Существует только одна моноклинная решетка Браве в двух измерениях: наклонная решетка.
Трехмерный
Существуют две моноклинические решетки Браве: примитивная моноклиническая и базоцентрированная моноклиническая решетка.
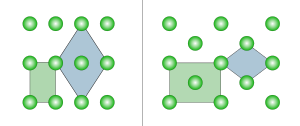
| Решетка Браве | Примитивный моноклинический | По центру основания моноклинический |
|---|---|---|
| Символ Пирсона | mP | РС |
| Стандарт ячейка | 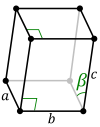 |  |
| Косой ромбический призма ячейка | 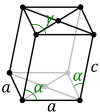 |  |
В моноклинной системе редко используется второй выбор кристаллических осей, в результате чего элементарная ячейка имеет форму наклонной ромбической призмы;[1] он может быть построен, потому что прямоугольный двумерный базовый слой также можно описать ромбическими осями. В этой настройке оси примитивные решетки и решетки с центром в основании меняются местами по типу центрирования.
Кристалл классы
В таблице ниже пространственные группы моноклинной кристаллической системы организованы по классам кристаллов. В нем перечислены Международные таблицы номеров пространственных групп кристаллографии.[2] за которым следует имя класса кристалла, его точечная группа в Обозначение Шенфлиса, Обозначение Германа – Могена (международное), орбифолд обозначения и обозначения Кокстера, дескрипторы типов, примеры минералов и обозначения для космические группы.
| # | Группа точек | Тип | Пример | Космические группы | |||||
|---|---|---|---|---|---|---|---|---|---|
| Имя[3] | Schön. | Intl | Сфера. | Кокс. | Примитивный | По центру основания | |||
| 3–5 | Клиновидный | C2 | 2 | 22 | [2]+ | энантиоморфный полярный | галотрихит | P2, P21 | C2 |
| 6–9 | Domatic | Cs (C1 час) | м | *11 | [ ] | полярный | хильгардит | Pm, Pc | См, см |
| 10–12 | Призматический | C2ч | 2 / м | 2* | [2,2+] | центросимметричный | гипс | P2 / м, P21/ м | C2 / м |
| 13–15 | P2 / c, P21/ c | C2 / c | |||||||
Клиновидный также является моноклинным гемиморфным; Domatic также является моноклиническим полуэдромом; Призматический также является нормальным моноклиническим.
Три моноклинических гемиморфных пространственных группы следующие:
- призма с поперечным сечением обои группа p2
- то же самое с винтовыми осями вместо осей
- то же самое с осями винта, а также осями, параллельными, между ними; в этом случае дополнительный вектор переноса - это половина вектора переноса в базовой плоскости плюс половина перпендикулярного вектора между базовыми плоскостями.
Четыре моноклинные полуэдральные пространственные группы включают
- с чистым отражением в основании призмы и на полпути
- те, у которых плоскости скольжения вместо плоскостей чистого отражения; скольжение - это половина вектора перемещения в базовой плоскости
- те, где оба находятся между собой; в этом случае дополнительный вектор перемещения - это скольжение плюс половина перпендикулярного вектора между базовыми плоскостями.
Смотрите также
Рекомендации
- ^ Видеть Хан (2002), п. 746, строка mC, столбец Primitive, где параметры ячейки заданы как a1 = a2, α = β
- ^ Князь, Э., изд. (2006). Международные таблицы для кристаллографии. Международный союз кристаллографии. Дои:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9.
- ^ «32 кристаллических класса». Получено 2018-06-19.
дальнейшее чтение
- Hurlbut, Cornelius S .; Кляйн, Корнелс (1985). Руководство по минералогии (20-е изд.). стр.69–73. ISBN 0-471-80580-7.
- Хан, Тео, изд. (2002). Международные таблицы для кристаллографии, том A: Симметрия пространственных групп. Международные таблицы для кристаллографии. А (5-е изд.). Берлин, Нью-Йорк: Springer-Verlag. Дои:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.CS1 maint: ref = harv (связь)
