Сглаживание - Википедия - Aliasing

Правильно подобранное изображение кирпичной стены требует экран достаточного разрешающая способность чтобы предотвратить муаровый узор

Пространственный алиасинг в виде муарового узора

В обработка сигналов и смежные дисциплины, сглаживание это эффект, из-за которого разные сигналы становятся неразличимыми (или псевдонимы друг друга), когда отобранный. Это также часто относится к искажение или же артефакт это происходит, когда сигнал, восстановленный из выборок, отличается от исходного непрерывного сигнала.

Псевдонимы могут возникать в сигналах, дискретизированных по времени, например цифровой звук, и называется временное алиасинг. Это также может происходить в сигналах с пространственной дискретизацией (например, муаровые узоры в цифровые изображения ); этот тип алиасинга называется пространственное искажение.

Псевдонима обычно избегают, применяя фильтры нижних частот или же фильтры сглаживания (AAF) к входному сигналу перед дискретизацией и при преобразовании сигнала из более высокой в более низкую частоту дискретизации. Подходящий реконструкция фильтрации затем следует использовать при восстановлении дискретизированного сигнала в непрерывной области или преобразовании сигнала с более низкой частоты дискретизации на более высокую. За пространственное сглаживание, типы сглаживания включают быстрое сглаживание сэмплов (FSAA), мультисэмпловое сглаживание, и суперсэмплинг.

Описание

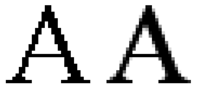
Слева: изображение буквы с псевдонимом. А в Times New Roman. Справа: An сглаженный изображение. (Смотрите также: Растеризация шрифтов )

При просмотре цифрового изображения реконструкция выполняется дисплеем или принтером, а также глазами и мозгом. Если данные изображения каким-либо образом обрабатываются во время выборки или реконструкции, восстановленное изображение будет отличаться от исходного изображения, и будет виден псевдоним.

Примером пространственного алиасинга является муаровый узор наблюдается на плохо пиксельном изображении кирпичной стены. Пространственное сглаживание методы избегают такой плохой пикселизации. Наложение может быть вызвано этапом выборки или этапом восстановления; их можно отличить, вызвав псевдоним выборки предварительная обработка и реконструкция алиасинга почтовая рассылка.^[1]

Временное алиасинг является серьезной проблемой при дискретизации видео- и аудиосигналов. Музыка, например, может содержать высокочастотные компоненты, которые не слышны людям. Если музыкальное произведение отобрано на 32000 выборок в секунду (Гц), любые частотные составляющие не ниже 16000 Гц (в Частота Найквиста для этой частоты дискретизации) вызовет алиасинг при воспроизведении музыки цифро-аналоговый преобразователь (ЦАП). Высокие частоты в аналоговом сигнале будут отображаться как более низкие частоты (неправильный псевдоним) в записанном цифровом сэмпле и, следовательно, не могут быть воспроизведены ЦАП. Чтобы предотвратить это, фильтр сглаживания используется для удаления компонентов выше частоты Найквиста перед отбором проб.

В видео или кинематографе временное алиасинг возникает из-за ограниченной частоты кадров и вызывает эффект вагона-колеса, в результате чего колесо со спицами вращается слишком медленно или даже в обратном направлении. Псевдонимы изменили кажущуюся частоту вращения. Изменение направления можно описать как отрицательная частота. Частоты временного наложения в видео и кинематографии определяются частотой кадров камеры, но относительная интенсивность частот наложения определяется временем срабатывания затвора (время экспозиции) или использованием фильтра уменьшения временного наложения во время съемки.^[2]^{[ненадежный источник? ]}

Как и в случае с видеокамерой, большинство схем выборки являются периодическими; то есть у них есть характеристика частота дискретизации во времени или в пространстве. Цифровые камеры предоставляют определенное количество образцов (пиксели ) на градус или на радиан, или отсчетов на мм в фокальной плоскости камеры. Аудиосигналы дискретизируются (оцифрованный ) с аналого-цифровой преобразователь, который производит постоянное количество выборок в секунду. Некоторые из наиболее ярких и тонких примеров наложения спектров возникают, когда дискретизируемый сигнал также имеет периодическое содержание.

Ограниченные функции

Фактические сигналы имеют конечную продолжительность и их частотную составляющую, как определено преобразование Фурье, не имеет верхней границы. При сэмплировании таких функций всегда возникает некоторая степень алиасинга. Функции, частотный состав которых ограничен (ограниченный диапазон) имеют бесконечную продолжительность во временной области. При достаточно высокой частоте дискретизации, определяемой пропускная способность, исходная функция теоретически может быть полностью восстановлена по бесконечному набору выборок.

Полосные сигналы

Иногда псевдонимы преднамеренно используются для сигналов без низкочастотного содержимого, что называется Bandpass сигналы. Недостаточная выборка, который создает низкочастотные псевдонимы, может дать тот же результат с меньшими усилиями, чем сдвиг частоты сигнала на более низкие частоты перед дискретизацией с более низкой частотой. Некоторые цифровые канализаторы^[3]использовать псевдонимы таким образом для повышения эффективности вычислений. Выборка (обработка сигнала), Частота Найквиста (относительно выборки), и Банк фильтров.

Выборочные синусоидальные функции

Синусоиды являются важным типом периодической функции, потому что реалистичные сигналы часто моделируются как сумма множества синусоид разных частот и разных амплитуд (например, с Ряд Фурье или же преобразовать ). Понимание того, что сглаживание делает с отдельными синусоидами, полезно для понимания того, что происходит с их суммой.

При выборке функции на частоте $ж s$ (интервалы $1/ ж s$ ) следующие функции времени $(т)$ дают идентичные наборы образцов: ${sin (2π (f + Nf s) т + φ), N = 0, \pm1, \pm2, \pm3,...$ }. А частотный спектр образцов дает одинаково сильные отклики на всех этих частотах. Без дополнительной информации частота исходной функции неоднозначна. Итак, функции и их частоты называются псевдонимы друг друга. Отмечая тригонометрическую идентичность:

{ displaystyle sin (2 pi (f + Nf _ { rm {s}}) t + phi) = left {{ begin {array} {ll} + sin (2 pi (f + Nf_ { rm {s}}) t + phi), & f + Nf _ { rm {s}} geq 0 - sin (2 pi | f + Nf _ { rm {s}} | t- phi), & f + Nf _ { rm {s}} <0 end {array}} right.}

мы можем записать все частоты псевдонимов как положительные значения: ${ Displaystyle е _ {_ {N}} (е) треугольник влево | е + Nf _ { rm {s}} вправо |}$ .

Две разные синусоиды, соответствующие одному набору образцов.

Например, здесь график изображает набор образцов с параметром $ж s = 1$ , и две разные синусоиды, которые могли дать образцы. Девять циклов красной синусоиды и один цикл синусоиды охватывают интервал в 10 отсчетов. Соответствующее количество циклов на образец находятся $ж красный = 0.9 ж s$ и $ж синий = 0.1 ж s$ . Итак $N = -1$ псевдоним $ж красный$ является $ж синий$ (наоборот).

Псевдоним имеет значение, когда кто-то пытается восстановить исходную форму волны из ее образцов. Самый распространенный метод реконструкции позволяет получить наименьший из $ж N (ж)$ частоты. Поэтому обычно важно, чтобы $ж 0 (ж)$ быть единственным минимумом. Необходимым и достаточным условием для этого является $ж s /2 > | ж |,$ куда $ж s /2$ обычно называют Частота Найквиста системы, которая производит выборку со скоростью $ж s .$ В нашем примере условие Найквиста выполняется, если исходным сигналом является синусоида синего цвета ( $ж = ж синий$ ). Но если $ж = ж красный = 0.9 ж s,$ обычный метод реконструкции даст синусоиду синего цвета вместо красной.

Складной

В приведенном выше примере $ж красный$ и $ж синий$ симметричны относительно частоты $ж s /2.$ И вообще как $ж$ увеличивается с 0 до $ж s /2,$ $ж -1 (ж)$ уменьшается с $ж s$ к $ж s /2.$ Аналогично, как $ж$ увеличивается с $ж s /2$ к $ж s,$ $ж -1 (ж)$ продолжает снижаться с $ж s /2$ до 0.

График зависимости амплитуды от частоты для одной синусоиды на частоте $0.6 ж s$ и некоторые из его псевдонимов на $0.4 ж s,$ $1.4 ж s,$ и $1.6 ж s$ будет выглядеть как 4 черные точки на первом рисунке ниже. Красными линиями обозначены пути (места ) из 4 точек, если бы мы настроили частоту и амплитуду синусоиды вдоль сплошного красного сегмента (между $ж s /2$ и $ж s$ ). Независимо от того, какую функцию мы выберем для изменения амплитуды в зависимости от частоты, график будет демонстрировать симметрию между 0 и $ж s .$ Эту симметрию обычно называют складывание, и другое название для $ж s /2$ (частота Найквиста) равна частота складывания. Складывание на практике часто наблюдается при просмотре частотный спектр образцов с реальной оценкой, таких как второй рисунок ниже.

Черные точки - это псевдонимы друг друга. Сплошная красная линия - это пример амплитуды, изменяющейся с частотой. Пунктирные красные линии - соответствующие пути псевдонимов.

Преобразование Фурье музыки, дискретизированной с частотой 44100 отсчетов в секунду, демонстрирует симметрию (называемую «сворачиванием») относительно частоты Найквиста (22050 Гц).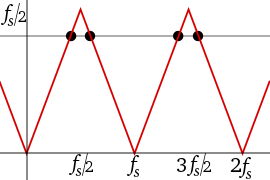

График частотного наложения, показывающий частоту сворачивания и периодичность. Частоты выше

ж s /2

есть псевдоним ниже

ж s /2,

значение которого представлено на этом графике.

Две сложные синусоиды, окрашенные в золотой и голубой цвета, которые соответствуют одним и тем же наборам реальных и мнимых точек выборки при выборке со скоростью (

ж s

), обозначенные линиями сетки. Показанный здесь случай:

ж голубой = ж -1 (ж золото) = ж золото - ж s

Сложные синусоиды

Сложные синусоиды осциллограммы, образцы которых сложные числа, а концепция отрицательная частота необходимо их различать. В этом случае частоты псевдонимов задаются просто: $ж N (ж) = ж + N f s .$ Следовательно, как $ж$ увеличивается с $ж s /2$ к $ж s,$ $ж -1 (ж)$ идет от $- ж s /2$ вверх до 0. Следовательно, сложные синусоиды не проявляют складывание. Сложные выборки синусоид с действительным знаком имеют мнимые части с нулевым знаком и демонстрируют сворачивание.

Частота выборки

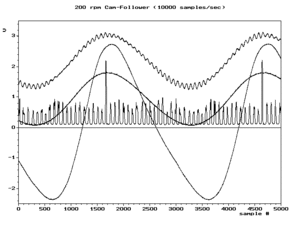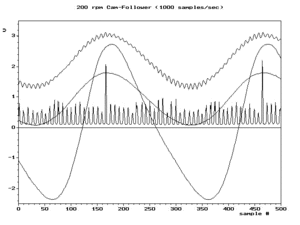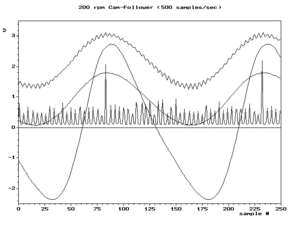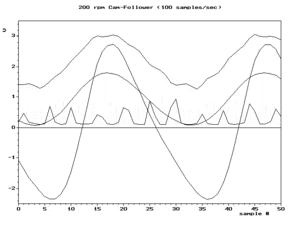
Иллюстрация 4 форм сигналов, восстановленных из выборок, взятых с шести разных частот. Два сигнала достаточно дискретизированы, чтобы избежать наложения спектров на всех шести частотах. Два других демонстрируют увеличение искажений (наложения спектров) при более низких скоростях.

Когда условие $ж s /2 > ж$ выполняется для самой высокой частотной составляющей исходного сигнала, затем она выполняется для всех частотных составляющих, условие, называемое Критерий Найквиста. Обычно это аппроксимируется путем фильтрации исходного сигнала для ослабления высокочастотных компонентов перед его дискретизацией. Эти ослабленные высокочастотные компоненты по-прежнему генерируют низкочастотные псевдонимы, но обычно с достаточно низкими амплитудами, чтобы не вызывать проблем. Фильтр, выбранный с учетом определенной частоты дискретизации, называется фильтр сглаживания.

Отфильтрованный сигнал впоследствии может быть восстановлен с помощью алгоритмов интерполяции без значительных дополнительных искажений. Большинство дискретизированных сигналов не просто сохраняются и реконструируются. Но верность теоретической реконструкции (через Формула интерполяции Уиттекера – Шеннона ) - обычная мера эффективности выборки.

Историческое использование

Исторически термин сглаживание произошли от радиотехники из-за действия супергетеродинные приемники. Когда приемник переключает несколько сигналов на более низкие частоты, с РФ к ЕСЛИ к гетеродинирование, нежелательный сигнал с радиочастоты, равно удаленной от гетеродин (LO) частота в качестве полезного сигнала, но не на той стороне гетеродина, может оказаться на той же частоте IF, что и желаемая. Если он достаточно сильный, он может помешать приему желаемого сигнала. Этот нежелательный сигнал известен как изображение или же псевдоним полезного сигнала.

Угловое алиасинг

Псевдонимы возникают всякий раз, когда использование дискретных элементов для захвата или создания непрерывного сигнала вызывает неоднозначность частоты.

Пространственное искажение, в частности угловой частоты, может происходить при воспроизведении световое поле^[4] или звуковое поле с дискретными элементами, как в 3D-дисплеи или же синтез волнового поля звука.

Этот псевдоним виден на изображениях, таких как плакаты с лентикулярная печать: если у них низкое угловое разрешение, то при движении мимо них, скажем слева направо, 2D-изображение изначально не изменяется (поэтому кажется, что оно перемещается влево), затем при переходе к следующему угловому изображению изображение внезапно меняется (так что оно прыгает вправо) - и частота и амплитуда этого движения из стороны в сторону соответствуют угловому разрешению изображения (и, для частоты, скорости бокового движения зрителя), что является угловым наложение светового поля 4D.

Отсутствие параллакс движения зрителя в 2D-изображениях и в 3-D фильм произведено стереоскопический очки (в 3D-фильмах эффект называется "рыскание ", поскольку изображение кажется вращающимся вокруг своей оси) аналогично можно рассматривать как потерю углового разрешения, при этом все угловые частоты смещаются на 0 (постоянный).

Еще примеры

Пример онлайн-аудио

Качественные эффекты наложения спектров можно услышать в следующей аудиодемонстрации. Шесть пилообразные волны играются последовательно, причем первые две пилы имеют основная частота 440 Гц (A4), вторые два имеют основную частоту 880 Гц (A5), а последние два - 1760 Гц (A6). Пилообразные зубы чередуются между ограниченный диапазон (без наложения) пилообразных и с наложенными зубцами, а частота дискретизации составляет 22,05 кГц. Пилообразные сигналы с ограниченной полосой частот синтезируются из сигналов пилообразной формы. Ряд Фурье такие, что нет гармоник выше Частота Найквиста присутствуют.

Искажение наложения спектров на более низких частотах становится все более очевидным с более высокими основными частотами, и хотя пилообразный зуб с ограниченным диапазоном все еще четкий на частоте 1760 Гц, зубчатый зуб с наложенным спектром искажается и становится резким с гудением, слышимым на частотах ниже основной.

Демонстрация наложения пилообразных зубьев

440 Гц с ограничением полосы, 440 Гц с наложением, 880 Гц с ограничением полосы, 880 Гц с наложением, 1760 Гц с ограничением, 1760 Гц с наложением

Проблемы с воспроизведением этого файла? Видеть помощь СМИ.

Определение направления

Форма пространственного наложения спектров также может возникать в антенных решетках или решетках микрофонов, используемых для оценки направления прихода волнового сигнала, как при геофизических исследованиях с помощью сейсмических волн. Волны должны отбираться более плотно, чем две точки за длина волны, или направление прихода волны становится неоднозначным.^[5]

Смотрите также

Примечания

Цитаты

^ Mitchell, Don P .; Нетравали, Арун Н. (Август 1988 г.). Реконструкция фильтров в компьютерной графике (PDF). ACM SIGGRAPH Международная конференция по компьютерной графике и интерактивным технологиям. 22. С. 221–228. Дои:10.1145/54852.378514. ISBN 0-89791-275-6.
^ Тессив, ООО (2010)."Технические пояснения к фильтру времени"
^ Харрис, Фредерик Дж. (Август 2006 г.). Многоскоростная обработка сигналов для систем связи. Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall PTR. ISBN 978-0-13-146511-4.
^ (Новый) Стэнфордский архив светового поля
^ Фланаган, Джеймс Л., "Ширина луча и полезная полоса пропускания микрофонных решеток с задержкой управления", AT&T Tech. Дж., 1985, 64, с. 983–995

дальнейшее чтение

Фарр, Мэтт; Хамфрис, Грег. (28 июня 2010 г.). Физический рендеринг: от теории к реализации. Морган Кауфманн. ISBN 978-0-12-375079-2. Глава 7 (Отбор проб и реконструкция). Проверено 3 марта 2013 года.

Наложение стробоскопического осциллографа на YouTube от Tektronix Application Engineer
Праймер для сглаживающих фильтров авторства La Vida Leica, обсуждает его назначение и влияние на записанные изображения.
Интерактивные примеры, демонстрирующие эффект алиасинга

[mitchell-1] Mitchell, Don P .; Нетравали, Арун Н. (Август 1988 г.). Реконструкция фильтров в компьютерной графике (PDF). ACM SIGGRAPH Международная конференция по компьютерной графике и интерактивным технологиям. 22. С. 221–228. Дои:10.1145/54852.378514. ISBN 0-89791-275-6.

[tessive-2] Тессив, ООО (2010)."Технические пояснения к фильтру времени"

[harris-3] Харрис, Фредерик Дж. (Август 2006 г.). Многоскоростная обработка сигналов для систем связи. Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall PTR. ISBN 978-0-13-146511-4.

[4] (Новый) Стэнфордский архив светового поля

[flangan-5] Фланаган, Джеймс Л., "Ширина луча и полезная полоса пропускания микрофонных решеток с задержкой управления", AT&T Tech. Дж., 1985, 64, с. 983–995

[1]

[2]

[3]

[4]

[5]

Цифровая обработка сигналов
Теория	Теория обнаружения Дискретный сигнал Теория оценок Теорема выборки Найквиста – Шеннона
Подполя	Обработка аудиосигнала Цифровая обработка изображений Обработка речи Статистическая обработка сигналов
Методы	Z-преобразование Расширенное z-преобразование Метод согласованного Z-преобразования Билинейное преобразование Constant-Q преобразование Дискретное косинусное преобразование (DCT) Дискретное преобразование Фурье (ДПФ) Дискретное преобразование Фурье (DTFT) Импульсная инвариантность Интегральное преобразование Преобразование Лапласа Формула обращения поста Помеченное преобразование Зак преобразовать
Отбор проб	Сглаживание Фильтр сглаживания Даунсэмплинг Курс Найквиста / частота Передискретизация Квантование Частота выборки Недостаточная выборка Передискретизация