Вязкость - Viscosity
| Вязкость | |
|---|---|
 Моделирование жидкостей с разной вязкостью. Жидкость справа имеет более высокую вязкость, чем жидкость слева. | |
Общие символы | η, μ |
Производные от другие количества | μ = грамм ·т |
| Часть серии по | ||||
| Механика сплошной среды | ||||
|---|---|---|---|---|
Законы
| ||||
В вязкость из жидкость является мерой его сопротивление к деформации с заданной скоростью. Для жидкостей это соответствует неформальному понятию «толщина»: например, сироп имеет более высокую вязкость, чем воды.[1]
Вязкость можно представить как количественную оценку внутреннего сила трения возникающий между соседними слоями жидкости, находящимися в относительном движении. Например, когда жидкость проталкивается через трубку, она течет быстрее у оси трубки, чем у ее стенок. В таком случае эксперименты показывают, что некоторые стресс (например, давление разница между двумя концами трубки) необходима для поддержания потока через трубку. Это связано с тем, что для преодоления трения между слоями жидкости, находящимися в относительном движении, требуется сила: сила этой силы пропорциональна вязкости.
Жидкость, не имеющая сопротивления напряжению сдвига, известна как идеальный или же невязкий жидкость. Нулевая вязкость наблюдается только при очень низкие температуры в сверхтекучие жидкости. В противном случае второй закон термодинамики требует, чтобы все жидкости имели положительную вязкость;[2][3] такие жидкости технически называются вязкими или вязкими. Жидкость с высокой вязкостью, например подача, может показаться твердый.
Этимология
Слово «вязкость» происходит от латинский вязкий ("омела "). Viscum также относится к вязкой клей полученный из ягод омелы.[4]
Определение
Простое определение
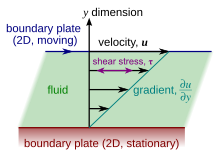

В материаловедение и инженерное дело, часто интересно понять силы, или подчеркивает, участвующие в деформация материала. Например, если бы материал был простой пружиной, ответ был бы следующим: Закон Гука, который говорит, что сила, испытываемая пружиной, пропорциональна расстоянию, смещенному от положения равновесия. Напряжения, которые можно отнести к деформации материала из некоторого состояния покоя, называются эластичный стрессы. В других материалах присутствуют напряжения, которые можно отнести к скорость изменения деформации через некоторое время. Это называется вязкими напряжениями. Например, в жидкости, такой как вода, напряжения, возникающие при сдвиге жидкости, не зависят от расстояние жидкость расслоена; скорее, они зависят от того, как быстро происходит срезание.
Вязкость - это свойство материала, которое связывает вязкие напряжения в материале со скоростью изменения деформации (скоростью деформации). Хотя это применимо к общим потокам, его легко визуализировать и определить в простом сдвиговом потоке, таком как плоский Поток Куэтта.
В потоке Куэтта жидкость удерживается между двумя бесконечно большими пластинами, одна неподвижная, а другая параллельно движущиеся с постоянной скоростью. (см. иллюстрацию справа). Если скорость верхней пластины достаточно мала (чтобы избежать турбулентности), то в установившемся режиме частицы жидкости движутся параллельно ей, и их скорость изменяется от внизу, чтобы на вершине.[5] Каждый слой жидкости движется быстрее, чем тот, что находится непосредственно под ним, и трение между ними вызывает сила сопротивляясь их относительному движению. В частности, жидкость прикладывает к верхней пластине силу в направлении, противоположном ее движению, и равную, но противоположную силу к нижней пластине. Поэтому требуется внешняя сила, чтобы верхняя пластина двигалась с постоянной скоростью.
Во многих жидкостях скорость потока изменяется линейно от нуля на дне до на вершине. Кроме того, величина силы, действующей на верхнюю пластину, оказывается пропорциональной скорости и область каждой пластины и обратно пропорционально их разделению :
Коэффициент пропорциональности вязкость жидкости в единицах (паскаль -второй ). Соотношение называется скорость деформации сдвига или же скорость сдвига, и является производная скорости жидкости в направлении перпендикуляр к пластинам (см. иллюстрации справа). Если скорость не изменяется линейно с , то подходящее обобщение
куда , и - местная скорость сдвига. Это выражение называется законом вязкости Ньютона. В сдвиговых потоках с плоской симметрией это то, что определяет . Это частный случай общего определения вязкости (см. Ниже), который может быть выражен в безкоординатной форме.
Использование Греческая буква мю () для вязкости распространено среди механический и инженеры-химики, а также физики.[6][7][8] Тем не менее Греческая буква эта () также используется химиками, физиками и ИЮПАК.[9] Вязкость иногда также называют сдвиговая вязкость. Однако, по крайней мере, один автор не рекомендует использовать эту терминологию, отмечая, что Помимо сдвиговых потоков, они могут возникать в несдвиговых потоках.[10]
Общее определение
В очень общих чертах вязкие напряжения в жидкости определяются как возникающие в результате относительной скорости различных частиц жидкости. Таким образом, вязкие напряжения должны зависеть от пространственных градиентов скорости потока. Если градиенты скорости малы, то вязкие напряжения в первом приближении зависят только от первых производных скорости.[11] (Для ньютоновских жидкостей это также линейная зависимость.) В декартовых координатах общее соотношение может быть записано как
куда - тензор вязкости, отображающий градиент скорости тензор на тензор вязких напряжений .[12] Поскольку индексы в этом выражении могут изменяться от 1 до 3, имеется 81 «коэффициент вязкости». в итоге. Однако если предположить, что тензор 4 ранга вязкости имеет вид изотропный сводит эти 81 коэффициент к трем независимым параметрам , , :
кроме того, предполагается, что вязкие силы не могут возникнуть, когда жидкость совершает простое вращение твердого тела, таким образом , оставив только два независимых параметра.[11] Наиболее обычное разложение по стандартной (скалярной) вязкости и объемная вязкость такой, что и . В векторной записи это выглядит как:
куда - единичный тензор, а кинжал обозначает транспонировать.[10][13] Это уравнение можно рассматривать как обобщенную форму закона вязкости Ньютона.
Объемная вязкость (также называемая объемной вязкостью) выражает тип внутреннего трения, которое сопротивляется сжатию или расширению жидкости без сдвига. Знание часто не требуется в задачах гидродинамики. Например, несжимаемая жидкость удовлетворяет и поэтому термин, содержащий выпадает. Более того, часто считается незначительным для газов, поскольку в одноатомный идеальный газ.[10] Одна ситуация, в которой может иметь значение расчет потерь энергии в звук и ударные волны, описанный Закон Стокса затухания звука, поскольку эти явления связаны с быстрым расширением и сжатием.
Стоит подчеркнуть, что приведенные выше выражения не являются фундаментальными законами природы, а скорее определениями вязкости. Таким образом, их пригодность для любого данного материала, а также средства для измерения или расчета вязкости должны определяться с использованием отдельных средств.
Динамическая и кинематическая вязкость
В гидродинамике принято работать в терминах кинематическая вязкость (также называемый «коэффициент диффузии по импульсу»), определяемый как отношение вязкости μ к плотность жидкости ρ. Обычно обозначается Греческая буква ню (ν) и имеет измерение :
В соответствии с этой номенклатурой вязкость часто называют динамическая вязкость или же абсолютная вязкость, и имеет единицы сила × время / площадь.
Импульсный транспорт
Теория переноса предлагает альтернативную интерпретацию вязкости с точки зрения переноса количества движения: вязкость - это свойство материала, которое характеризует перенос количества движения в жидкости, как и теплопроводность характеризует высокая температура транспорт, и (масса) диффузионность характеризует массовый транспорт.[14] Чтобы убедиться в этом, обратите внимание, что в законе вязкости Ньютона , напряжение сдвига имеет единицы, эквивалентные импульсу поток, то есть импульс в единицу времени на единицу площади. Таким образом, можно интерпретировать как определение потока импульса в направление от одного слоя жидкости к другому. Согласно закону вязкости Ньютона, этот поток импульса происходит через градиент скорости, а величина соответствующего потока импульса определяется вязкостью.
Аналогию с тепломассопереносом можно сделать явной. Подобно тому, как тепло течет от высокой температуры к низкой температуре, а масса течет от высокой плотности к низкой, импульс течет от высокой скорости к низкой. Все это поведение описывается компактными выражениями, называемыми учредительные отношения, одномерные формы которых приведены здесь:
куда это плотность, и - потоки массы и тепла, и - массовая диффузия и теплопроводность.[15] Тот факт, что перенос массы, импульса и энергии (тепла) являются одними из наиболее важных процессов в механике сплошной среды, не случаен: это одни из немногих физических величин, которые сохраняются на микроскопическом уровне при межчастичных столкновениях. Таким образом, вместо того, чтобы быть продиктованной быстрой и сложной шкалой времени микроскопического взаимодействия, их динамика происходит в масштабе макроскопического времени, как описано различными уравнениями теории переноса и гидродинамики.
Ньютоновские и неньютоновские жидкости
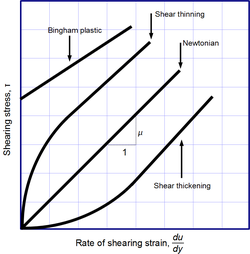
Закон вязкости Ньютона - это не фундаментальный закон природы, а скорее конститутивное уравнение (подобно Закон Гука, Закон Фика, и Закон Ома ), который служит для определения вязкости . Его форма мотивирована экспериментами, которые показывают, что для широкого диапазона жидкостей не зависит от скорости деформации. Такие жидкости называются Ньютоновский. Газы, воды, и многие обычные жидкости можно считать ньютоновскими в обычных условиях и контекстах. Однако есть много неньютоновские жидкости которые значительно отклоняются от этого поведения. Например:
- Утолщение при сдвиге жидкости, вязкость которых увеличивается со скоростью деформации сдвига.
- Истончение сдвига жидкости, вязкость которых уменьшается со скоростью деформации сдвига.
- Тиксотропный жидкости, которые со временем становятся менее вязкими при встряхивании, взбалтывании или другом напряжении.
- Реопектический (дилатантные) жидкости, которые со временем становятся более вязкими при встряхивании, взбалтывании или другом напряжении.
- Пластмассы Бингема которые ведут себя как твердое тело при низких напряжениях, но текут как вязкая жидкость при высоких напряжениях.
Форель соотношение - это соотношение вязкость при растяжении к сдвиговая вязкость. Для ньютоновской жидкости коэффициент Траутона равен 3.[16][17] Жидкости, разжижающие сдвиг, очень часто, но ошибочно, называют тиксотропными.[18]
Даже для ньютоновской жидкости вязкость обычно зависит от ее состава и температуры. Для газов и др. сжимаемые жидкости, он зависит от температуры и очень медленно меняется с давлением. Вязкость некоторых жидкостей может зависеть от других факторов. А магнитореологическая жидкость, например, становится толще при воздействии магнитное поле, возможно, до такой степени, что ведет себя как твердое тело.
В твердых телах
Силы вязкости, возникающие при течении жидкости, не следует путать с эластичный силы, возникающие в твердом теле в ответ на напряжения сдвига, сжатия или растяжения. В последнем случае напряжение пропорционально количество деформации сдвига, в жидкости она пропорциональна ставка деформации с течением времени. (По этой причине, Максвелл использовал термин летучая эластичность для вязкости жидкости.)
Однако многие жидкости (включая воду) кратковременно реагируют как упругие твердые тела, когда подвергаются внезапному напряжению. И наоборот, многие «твердые тела» (даже гранит ) будет течь как жидкость, хотя и очень медленно, даже при сколь угодно малой нагрузке.[19] Поэтому такие материалы лучше всего описать как обладающие как эластичностью (реакция на деформацию), так и вязкостью (реакция на скорость деформации); то есть быть вязкоупругий.
Вязкоупругие твердые вещества могут проявлять как вязкость при сдвиге, так и объемную вязкость. В вязкость при растяжении это линейная комбинация сдвиговой и объемной вязкости, которая описывает реакцию твердого эластичного материала на удлинение. Он широко используется для характеристики полимеров.
В геология, земляные материалы, демонстрирующие вязкую деформацию не менее трех порядки величины больше, чем их упругая деформация, иногда называют рейды.[20]
Измерение
Вязкость измеряется с различными типами вискозиметры и реометры. Реометр используется для тех жидкостей, которые не могут быть определены одним значением вязкости и, следовательно, требуют установки и измерения большего числа параметров, чем в случае с вискозиметром. Тщательный контроль температуры жидкости необходим для получения точных измерений, особенно для таких материалов, как смазочные материалы, вязкость которых может удвоиться при изменении всего на 5 ° C.[21]
Для некоторых жидкостей вязкость постоянна в широком диапазоне скоростей сдвига (Ньютоновские жидкости ). Жидкости без постоянной вязкости (неньютоновские жидкости ) нельзя описать одним числом. Неньютоновские жидкости демонстрируют множество различных корреляций между напряжением сдвига и скоростью сдвига.
Одним из наиболее распространенных инструментов для измерения кинематической вязкости является стеклянный капиллярный вискозиметр.
В покрытие промышленности, вязкость может быть измерена с помощью чашки, в которой время истечения измеряется. Есть несколько видов чашек, например Чашка Zahn и Чашка вязкости Форда - использование каждого типа варьируется в основном в зависимости от отрасли. Время истечения также можно преобразовать в кинематическую вязкость (сантистокс, сСт) с помощью уравнений преобразования.
Вискозиметр Stormer, также используемый в покрытиях, использует вращение в зависимости от нагрузки для определения вязкости. Вязкость указывается в единицах Кребса (KU), которые являются уникальными для вискозиметров Stormer.
Вибрационные вискозиметры также можно использовать для измерения вязкости. Резонансные или вибрационные вискозиметры работают, создавая поперечные волны в жидкости. В этом методе датчик погружается в жидкость и заставляется резонировать на определенной частоте. Поскольку поверхность датчика рассекает жидкость, энергия теряется из-за ее вязкости. Затем эта рассеиваемая энергия измеряется и преобразуется в показание вязкости. Более высокая вязкость вызывает большие потери энергии.[нужна цитата ]
Вязкость при растяжении можно измерить с помощью различных реометры которые применяются напряжение растяжения.
Объемная вязкость можно измерить с помощью акустический реометр.
Кажущаяся вязкость это расчет, полученный на основе испытаний, проведенных на буровой раствор используется при разработке нефтяных или газовых скважин. Эти расчеты и испытания помогают инженерам разрабатывать и поддерживать свойства бурового раствора в соответствии с требуемыми спецификациями.
Нановязкость (вязкость, измеряемая нанозондами) может быть измерена Флуоресцентная корреляционная спектроскопия.[22]
Единицы
В SI единицей динамической вязкости является ньютон -секунда на квадратный метр (Н · с / м2), также часто выражаются в эквивалентных формах паскаль -второй (Па · с) и килограмм на метр в секунду (кг · м−1· С−1). В CGS единица равновесие (P, или г · см−1· С−1 = 0,1 Па · с),[23] названный в честь Жан Леонар Мари Пуазей. Обычно это выражается, особенно в ASTM стандарты, как сантипуаз (сП), потому что это более удобно (например, вязкость воды при 20 ° C составляет около 1 сП), а один сантипуаз равен миллипаскалям в секунду в системе СИ (мПа · с).
Единица измерения кинематической вязкости в системе СИ - квадратный метр в секунду (м2/ с), тогда как единицей измерения кинематической вязкости в системе CGS является топки (Ст, или см2· С−1 = 0,0001 м2· С−1), названный в честь сэра Джордж Габриэль Стоукс.[24] В США топить иногда используется как форма единственного числа. В частичный сантистоксы (сСт) часто используется вместо 1 сСт = 1 мм2· С−1 = 10−6 м2· С−1. Кинематическая вязкость воды при 20 ° C составляет около 1 сСт.
Наиболее часто используемые системы Американская обычная или имперская, единицы - это Британский гравитационный (BG) и Английский инженерный (EE). В системе BG динамическая вязкость имеет единицы измерения фунт -секунд на квадрат оплачивать (фунт · с / фут2), а в системе ЭЭ - единицы фунт-сила -секунд на квадратный фут (фунт-сила · с / фут2). Обратите внимание, что фунт и фунт-сила эквивалентны; эти две системы отличаются только тем, как определяются сила и масса. В системе BG фунт является базовой единицей, от которой единица массы ( слизняк ) определяется Второй закон Ньютона, тогда как в системе EE единицы силы и массы (фунт-сила и фунт-масса соответственно) определяются независимо через Второй закон с использованием константа пропорциональности граммc.
Кинематическая вязкость измеряется в квадратных футах в секунду (ft2/ s) в системах BG и EE.
Нестандартные единицы включают Рейн, британская единица динамической вязкости.[нужна цитата ] В автомобильной промышленности индекс вязкости используется для описания изменения вязкости с температурой.
В взаимный вязкости текучесть, обычно обозначаемый или же , в зависимости от используемого соглашения, измеряется в взаимное равновесие (П−1, или же см ·s ·грамм−1), иногда называемый ре. Текучесть редко используется в инженерное дело упражняться.
Когда-то нефтяная промышленность полагалась на измерение кинематической вязкости с помощью Вискозиметр Сейболта, и выражая кинематическую вязкость в единицах Универсальные секундные стрелки Saybolt (SUS).[25] Другие сокращения, такие как SSU (Сэйболт секундомер универсальный) или внедорожник (Универсальная вязкость по Сейболту) иногда используются. Кинематическая вязкость в сантистоксах может быть преобразована из SUS в соответствии с арифметическими расчетами и справочной таблицей, приведенной в ASTM D 2161.
Молекулярное происхождение
В общем, вязкость системы подробно зависит от того, как взаимодействуют молекулы, составляющие систему. Нет простых, но правильных выражений для вязкости жидкости. Простейшие точные выражения - это Отношения Грина – Кубо для линейной сдвиговой вязкости или нестационарная временная корреляционная функция выражения, полученные Эвансом и Морриссом в 1988 г.[26] Хотя каждое из этих выражений является точным, вычисление вязкости плотной жидкости с использованием этих соотношений в настоящее время требует использования молекулярная динамика компьютерное моделирование. С другой стороны, можно добиться гораздо большего прогресса в отношении разреженного газа.Даже элементарные предположения о том, как молекулы газа движутся и взаимодействуют, приводят к основному пониманию молекулярного происхождения вязкости. Более сложные обработки могут быть созданы путем систематического грубого измельчения уравнения движения молекул газа. Примером такого лечения является Теория Чепмена – Энскога, который выводит выражения для вязкости разреженного газа из Уравнение Больцмана.[27]
Перенос импульса в газах обычно обеспечивается дискретными столкновениями молекул, а в жидкостях - силами притяжения, которые связывают молекулы близко друг к другу.[14] Из-за этого динамическая вязкость жидкостей обычно намного больше, чем у газов.
Чистые газы
Элементарный расчет вязкости для разреженного газа Рассмотрим разреженный газ, движущийся параллельно -ось со скоростью это зависит только от координировать. Чтобы упростить обсуждение, предполагается, что газ имеет однородную температуру и плотность.
При этих предположениях скорость молекулы, проходящей через равна той скорости, которую имела молекула, когда ее длина свободного пробега началось. Потому что обычно мала по сравнению с макроскопическими масштабами, средняя скорость такой молекулы имеет вид
куда числовая константа порядка . (Некоторые авторы оценивают ;[14][28] с другой стороны, более тщательный расчет для жестких упругих сфер дает .) Теперь, потому что половина молекулы по обе стороны движутся к , и в среднем это делается с половина то средняя молекулярная скорость , поток импульса с обеих сторон равен
В сеть поток импульса на разница между ними:
Согласно определению вязкости, этот поток импульса должен быть равен , что приводит к
Вязкость газов возникает в основном из-за молекулярная диффузия который передает импульс между слоями потока. Элементарный расчет для разреженного газа при температуре и плотность дает
куда это Постоянная Больцмана, молекулярная масса, и числовая константа порядка . Количество , то длина свободного пробега, измеряет среднее расстояние, которое молекула проходит между столкновениями. Даже без априори знание , это выражение имеет интересный смысл. В частности, поскольку обычно обратно пропорциональна плотности и увеличивается с температурой, сам должен увеличиваться с температурой и быть независимый плотности при фиксированной температуре. Фактически, оба этих предсказания сохраняются при более сложных методах лечения и точно описывают экспериментальные наблюдения. Обратите внимание, что такое поведение противоречит общепринятому мнению о жидкостях, для которых вязкость обычно уменьшается с температурой.[14][28]
Для жестких упругих сфер диаметром , можно вычислить, давая
В этом случае не зависит от температуры, поэтому . Однако для более сложных молекулярных моделей зависит от температуры нетривиальным образом, и простые кинетические аргументы, используемые здесь, неадекватны. В более фундаментальном плане понятие длины свободного пробега становится неточным для частиц, которые взаимодействуют в конечном диапазоне, что ограничивает полезность концепции для описания реальных газов.[29]
Теория Чепмена – Энскога
Техника, разработанная Сидней Чепмен и Дэвид Энског в начале 1900-х годов позволяет более точно рассчитать .[27] Он основан на Уравнение Больцмана, который обеспечивает систематическое статистическое описание разреженного газа с точки зрения межмолекулярных взаимодействий.[30] Таким образом, их метод позволяет точно рассчитать для более реалистичных молекулярных моделей, таких как те, которые включают межмолекулярное притяжение, а не просто жесткое отталкивание.
Оказывается, более реалистичное моделирование взаимодействий необходимо для точного прогнозирования температурной зависимости , который, как показывают эксперименты, увеличивается быстрее, чем прогнозируемый тренд для жестких упругих сфер.[14] Действительно, анализ Чепмена-Энскога показывает, что предсказываемая температурная зависимость может быть настроена путем изменения параметров в различных молекулярных моделях. Простым примером является модель Сазерленда,[а] который описывает жесткие упругие сферы с слабый взаимная симпатия. В таком случае силу притяжения можно рассматривать пертурбативно, что приводит к особенно простому выражению для :
куда не зависит от температуры, а определяется только параметрами межмолекулярного притяжения. Для связи с экспериментом удобно переписать как
куда вязкость при температуре .[31] Если известно из экспериментов на и хотя бы еще одну температуру, тогда можно рассчитать. Оказывается, выражения для полученные таким образом точны для ряда газов в значительном диапазоне температур. С другой стороны, Чепмен и Коулинг 1970 утверждают, что этот успех не означает, что молекулы действительно взаимодействуют в соответствии с моделью Сазерленда. Скорее они интерпретируют предсказание для как простая интерполяция, которая действительна для некоторых газов в фиксированных диапазонах температур, но в остальном не дает принципиально правильной и общей картины межмолекулярных взаимодействий. Чуть более сложные модели, такие как Потенциал Леннарда-Джонса, может обеспечить лучшее изображение, но только за счет более непрозрачной зависимости от температуры. В некоторых системах также необходимо отказаться от предположения о сферической симметрии, как это имеет место для паров с высокой полярные молекулы подобно ЧАС2О.[32][33]
Объемная вязкость
В кинетико-молекулярной картине ненулевая объемная вязкость возникает в газах всякий раз, когда существуют значительные релаксационные временные рамки, управляющие обменом энергией между поступательной энергией молекул и их внутренней энергией, например вращающийся и колебательный. Таким образом, объемная вязкость составляет для одноатомного идеального газа, в котором внутренняя энергия молекул пренебрежимо мала, но отлична от нуля для такого газа, как углекислый газ, молекулы которого обладают как вращательной, так и колебательной энергией.[34][35]
Чистые жидкости
В отличие от газов, нет простой, но точной картины молекулярного происхождения вязкости жидкостей.
На простейшем уровне описания относительному движению соседних слоев в жидкости противодействуют прежде всего силы притяжения, действующие через границу слоя. На этом изображении (правильно) ожидается, что вязкость будет уменьшаться с увеличением температуры. Это связано с тем, что повышение температуры увеличивает случайное тепловое движение молекул, что облегчает им преодоление их взаимодействий притяжения.[36]
Основываясь на этой визуализации, можно построить простую теорию по аналогии с дискретной структурой твердого тела: группы молекул в жидкости визуализируются как образующие «клетки», которые окружают и заключают в себя отдельные молекулы.[37] Эти клетки могут быть заняты или не заняты, и более сильное молекулярное притяжение соответствует более сильным клеткам. Из-за случайного теплового движения молекула «прыгает» между клетками со скоростью, которая обратно пропорциональна силе молекулярного притяжения. В равновесие эти «прыжки» не смещены в каком-либо направлении. С другой стороны, для того, чтобы два соседних слоя перемещались относительно друг друга, «прыжки» должны быть смещены в направлении относительного движения. Сила, необходимая для поддержания этого направленного движения, может быть оценена для данной скорости сдвига, что приводит к
(1)
куда это Константа Авогадро, это Постоянная Планка, объем крот жидкости, и это нормальная точка кипения. Этот результат имеет ту же форму, что и широко распространенное и точное эмпирическое соотношение
(2)
куда и - константы, соответствующие данным.[37][38] С другой стороны, некоторые авторы проявляют осторожность в отношении этой модели: ошибки до 30% могут быть обнаружены с помощью уравнения (1) по сравнению с уравнением подгонки (2) к экспериментальным данным.[37] Говоря более фундаментально, физические допущения, лежащие в основе уравнения (1) подверглись критике.[39] Также утверждалось, что экспоненциальная зависимость в уравнении (1) не обязательно описывает экспериментальные наблюдения более точно, чем более простые неэкспоненциальные выражения.[40][41]
В свете этих недостатков разработка менее специальной модели представляет практический интерес. Вместо простоты в пользу точности можно написать строгие выражения для вязкости, исходя из фундаментальных уравнений движения молекул. Классическим примером такого подхода является теория Ирвинга – Кирквуда.[42] С другой стороны, такие выражения даются как средние по многочастичным корреляционные функции и поэтому их сложно применить на практике.
В общем, полученные эмпирическим путем выражения (основанные на существующих измерениях вязкости), по-видимому, являются единственным неизменно надежным средством расчета вязкости жидкостей.[43]
Смеси и смеси
Газовые смеси
Та же молекулярно-кинетическая картина однокомпонентного газа может быть применена и к газовой смеси. Например, в подходе Чепмена – Энскога вязкость бинарной смеси газов можно записать через вязкости отдельных компонентов , их соответствующие объемные доли и межмолекулярные взаимодействия.[27] Что касается однокомпонентного газа, то зависимость от параметров межмолекулярных взаимодействий входит через различные интегралы столкновений, которые не могут быть выражены в терминах элементарных функций. Чтобы получить полезные выражения для которые разумно соответствуют экспериментальным данным, интегралы столкновений обычно должны оцениваться с использованием некоторой комбинации аналитических вычислений и эмпирической подгонки. Примером такой процедуры является рассмотренный выше подход Сазерленда для однокомпонентного газа.
Смеси жидкостей
Что касается чистых жидкостей, вязкость смеси жидкостей трудно предсказать на основе молекулярных принципов. Один из методов - расширить теорию молекулярной «клетки», представленную выше, на чистую жидкость. Это можно сделать с разной степенью сложности. Одним из полезных выражений, полученных в результате такого анализа, является уравнение Ледерера – Роджерса для бинарной смеси:
куда - эмпирический параметр, а и соответствующие мольные доли и вязкости составляющих жидкостей.[44]
Поскольку смешивание является важным процессом в смазочной и нефтяной промышленности, существует множество эмпирических и соответствующих уравнений для прогнозирования вязкости смеси, помимо тех, которые вытекают непосредственно из молекулярной теории.[44]
Растворы и суспензии
Водные решения
В зависимости от растворенный и диапазон концентрации, водный электролит раствор может иметь большую или меньшую вязкость по сравнению с чистой водой при той же температуре и давлении. Например, 20% физиологический раствор (хлорид натрия ) вязкость раствора более чем в 1,5 раза выше вязкости чистой воды, тогда как 20% йодистый калий раствор имеет вязкость примерно в 0,91 раза больше вязкости чистой воды.
Идеализированная модель разбавленных электролитических растворов приводит к следующему предсказанию вязкости решения:[45]
куда - вязкость растворителя, это концентрация, а является положительной константой, которая зависит как от растворителя, так и от свойств растворенного вещества. Однако это выражение действительно только для очень разбавленных растворов, имеющих менее 0,1 моль / л.[46] Для более высоких концентраций необходимы дополнительные члены, которые учитывают молекулярные корреляции более высокого порядка:
куда и подходят из данных. В частности, отрицательное значение может объяснить снижение вязкости, наблюдаемое в некоторых растворах. Расчетные значения этих констант приведены ниже для хлорида натрия и иодида калия при температуре 25 ° C (моль = крот, L = литр ).[45]
| Растворенное вещество | (моль−1/2 L1/2) | (моль−1 L) | (моль−2 L2) |
|---|---|---|---|
| Натрия хлорид (NaCl) | 0.0062 | 0.0793 | 0.0080 |
| Йодистый калий (KI) | 0.0047 | −0.0755 | 0.0000 |
Подвески
В суспензии твердых частиц (например, микрон -размерные сферы, взвешенные в масле), эффективная вязкость могут быть определены в терминах компонентов напряжения и деформации, которые усредняются по объему, большему по сравнению с расстоянием между взвешенными частицами, но малому по сравнению с макроскопическими размерами.[47] Такие суспензии обычно демонстрируют неньютоновское поведение. Однако для разбавленных систем в установившихся потоках поведение является ньютоновским, и выражения для могут быть получены непосредственно из динамики частицы. В очень разбавленной системе с объемной долей , взаимодействиями между взвешенными частицами можно пренебречь. В таком случае можно явно рассчитать поле потока вокруг каждой частицы независимо и объединить результаты для получения . Для сфер это приводит к уравнению Эйнштейна:
куда - вязкость суспендирующей жидкости. Линейная зависимость от является прямым следствием игнорирования межчастичных взаимодействий; в общем, у одного будет
где коэффициент может зависеть от формы частиц (например, сфер, стержней, дисков).[48] Экспериментальное определение точного значения однако сложно: даже предсказание для сфер не было окончательно подтверждено, с различными экспериментами, находящими значения в диапазоне . Этот недостаток объясняется трудностью контроля экспериментальных условий.[49]
В более плотных суспензиях приобретает нелинейную зависимость от , что указывает на важность межчастичных взаимодействий. Существуют различные аналитические и полуэмпирические схемы для определения этого режима. На самом базовом уровне термин, квадратичный по добавлен к :
а коэффициент соответствует экспериментальным данным или аппроксимируется микроскопической теорией. В целом, однако, следует проявлять осторожность при применении таких простых формул, поскольку неньютоновское поведение проявляется в плотных суспензиях ( для сфер),[49] или в суспензиях удлиненных или гибких частиц.[47]
Существует различие между суспензией твердых частиц, описанной выше, и эмульсия. Последний представляет собой суспензию крошечных капелек, которые сами по себе могут иметь внутреннюю циркуляцию. Наличие внутренней циркуляции может заметно снизить наблюдаемую эффективную вязкость, поэтому необходимо использовать различные теоретические или полуэмпирические модели.[50]
Аморфные материалы
В диапазоне высоких и низких температур вязкое течение в аморфные материалы (например, в очки и тает)[52][53][54] имеет Форма Аррениуса:
куда Q актуальный энергия активации, заданные в виде молекулярных параметров; Т это температура; р моляр газовая постоянная; и А приблизительно постоянная. Энергия активации Q принимает другое значение в зависимости от того, рассматривается ли верхний или нижний предел температуры: он изменяется с высокого значения QЧАС при низких температурах (в стеклообразном состоянии) до низкого значения QL при высоких температурах (в жидком состоянии).

Для промежуточных температур изменяется нетривиально с температурой, и простая форма Аррениуса не работает. С другой стороны, двухэкспоненциальное уравнение
куда , , , являются константами, обеспечивает хорошее соответствие экспериментальным данным во всем диапазоне температур, в то же время переходя к правильной форме Аррениуса в низких и высоких температурах. Помимо удобного подбора данных, это выражение также может быть получено из различных теоретических моделей аморфных материалов на атомном уровне.[53]
Двухэкспоненциальное уравнение для вязкости может быть получено в рамках модели Дайра-Шуинга для переохлажденных жидкостей, где энергетический барьер Аррениуса отождествляется с высокочастотным модуль сдвига раз характерный объем толкания.[55] После задания температурной зависимости модуля сдвига через тепловое расширение и через отталкивающую часть межмолекулярного потенциала восстанавливается еще одно двухэкспоненциальное уравнение[56]:
куда обозначает высокочастотный модуль сдвига материала, оцененного при температуре, равной стеклование температура , это так называемый объем выталкивания, т.е. это характерный объем группы атомов, участвующих в событии выталкивания, посредством которого атом / молекула выходит из клетки ближайших соседей, обычно порядка объема, занятого несколькими атомами. . Более того, это тепловое расширение коэффициент материала, является параметром, который измеряет крутизну степенного подъема восходящего фланга первого пика функция радиального распределения, и количественно связана с отталкивающей частью межатомный потенциал.[56] Ну наконец то, обозначает Постоянная Больцмана.
Вихревая вязкость
При изучении турбулентность в жидкости, общая практическая стратегия - игнорировать мелкомасштабные вихри (или же водовороты ) в движении и для расчета крупномасштабного движения с эффективный вязкость, называемая «вихревой вязкостью», которая характеризует перенос и рассеяние энергия в более мелкомасштабном потоке (см. моделирование больших вихрей ).[57][58] В отличие от вязкости самой жидкости, которая должна быть положительной из-за второй закон термодинамики, вихревая вязкость может быть отрицательной.[59][60]
Избранные вещества

Наблюдаемые значения вязкости различаются на несколько порядков даже для обычных веществ (см. Таблицу порядков величин ниже). Например, 70% раствор сахарозы (сахара) имеет вязкость в 400 раз больше, чем у воды, и в 26000 раз больше, чем у воздуха.[62] Более того, по оценкам, пек имеет вязкость в 230 миллиардов раз больше вязкости воды.[61]
Вода
В динамическая вязкость из воды составляет около 0,89 мПа · с при комнатной температуре (25 ° C). В зависимости от температуры в кельвины, вязкость можно оценить с помощью полуэмпирического Уравнение Фогеля-Фулчера-Таммана:
куда А = 0,02939 мПа · с, B = 507,88 К, а C = 149,3 К.[63] Значения вязкости, определенные экспериментально, также приведены в таблице ниже. Обратите внимание, что при 20 ° C динамическая вязкость составляет около 1 сП, а кинематическая вязкость составляет около 1 сСт.
| Температура (° C) | Вязкость (мПа · с или сП) |
|---|---|
| 10 | 1.3059 |
| 20 | 1.0016 |
| 30 | 0.79722 |
| 50 | 0.54652 |
| 70 | 0.40355 |
| 90 | 0.31417 |
Воздуха
При стандартных атмосферных условиях (25 ° C и давление 1 бар) динамическая вязкость воздуха составляет 18,5 мкПа · с, что примерно в 50 раз меньше вязкости воды при той же температуре. За исключением очень высокого давления, вязкость воздуха в основном зависит от температуры. Среди множества возможных приближенных формул для температурной зависимости (см. Температурная зависимость вязкости ), один:[64]
что является точным в диапазоне от -20 ° C до 400 ° C. Чтобы эта формула действовала, температура должна быть указана в кельвины; тогда соответствует вязкости в Па · с.

Другие распространенные вещества
| Вещество | Вязкость (мПа · с) | Температура (° C) | Ref. |
|---|---|---|---|
| Бензол | 0.604 | 25 | [62] |
| Вода | 1.0016 | 20 | |
| Меркурий | 1.526 | 25 | |
| Цельное молоко | 2.12 | 20 | [65] |
| Темное пиво | 2.53 | 20 | [66] |
| Оливковое масло | 56.2 | 26 | [65] |
| Медовый | 2000–10000 | 20 | [67] |
| Кетчуп[b] | 5000–20000 | 25 | [68] |
| Арахисовое масло[b] | 104–106 | [69] | |
| Подача | 2.3×1011 | 10–30 (переменная) | [61] |
Порядок оценки величины
В следующей таблице показан диапазон значений вязкости, наблюдаемый для обычных веществ. Если не указано иное, предполагается температура 25 ° C и давление 1 атмосфера. Некоторым веществам переменного состава или с неньютоновским поведением не присваиваются точные значения, поскольку в этих случаях вязкость зависит от дополнительных факторов, помимо температуры и давления.
| Фактор (Па · с) | Описание | Примеры | Значения (Па · с) | Ref. |
|---|---|---|---|---|
| 10−6 | Нижний диапазон газовой вязкости | Бутан | 7.49 × 10−6 | [70] |
| Водород | 8.8 × 10−6 | [71] | ||
| 10−5 | Верхний диапазон вязкости газа | Криптон | 2.538 × 10−5 | [72] |
| Неон | 3.175 × 10−5 | |||
| 10−4 | Нижний диапазон вязкости жидкости | Пентан | 2.24 × 10−4 | [62] |
| Бензин | 6 × 10−4 | |||
| Вода | 8.90 × 10−4 | [62] | ||
| 10−3 | Типичный диапазон для малых молекул Ньютоновские жидкости | Этиловый спирт | 1.074 × 10−3 | |
| Меркурий | 1.526 × 10−3 | |||
| Цельное молоко (20 ° С) | 2.12 × 10−3 | [65] | ||
| Кровь | 4 × 10−3 | |||
| 10−2 – 100 | Масла и углеводороды с длинной цепью | Льняное масло | 0.028 | |
| Оливковое масло | 0.084 | [65] | ||
| SAE 10 Моторное масло | От 0,085 до 0,14 | |||
| касторовое масло | 0.1 | |||
| SAE 20 Моторное масло | 0,14 до 0,42 | |||
| SAE 30 Моторное масло | 0,42–0,65 | |||
| SAE 40 Моторное масло | От 0,65 до 0,90 | |||
| Глицерин | 1.5 | |||
| Блинный сироп | 2.5 | |||
| 101 – 103 | Пасты, гели и прочие полутвердые вещества (обычно неньютоновский) | Кетчуп | ≈ 101 | [68] |
| Горчица | ||||
| Сметана | ≈ 102 | |||
| Арахисовое масло | [69] | |||
| Сало | ≈ 103 | |||
| ≈108 | Вязкоупругие полимеры | Подача | 2.3×108 | [61] |
| ≈1021 | Определенные твердые тела под вязкоупругими описание | Мантия (геология) | ≈ 1019 до 1024 | [73] |
Смотрите также
- Dashpot
- Число Деборы
- Дилатант
- Жидкость Гершеля – Балкли
- Синдром повышенной вязкости
- Собственная вязкость
- Невязкое течение
- Метод Joback (оценка вязкости жидкости по молекулярной структуре)
- Эффект Кая
- Микровязкость
- Число Мортона
- Давление масла
- Квазитвердый
- Реология
- Стокса поток
- Сверхтекучий гелий-4
- Вязкопластичность
- Модели вязкости для смесей
Рекомендации
Сноски
- ^ Следующее обсуждение основано на Чепмен и Коулинг 1970, стр. 232–237
- ^ а б Эти материалы очень неньютоновский.
Цитаты
- ^ Саймон 1971.
- ^ Балеску 1975 С. 428–429.
- ^ Ландау и Лифшиц 1987.
- ^ Харпер, Дуглас (без даты). viscous (прилаг.) вязкий. Интернет-словарь этимологии. Получено 19 сентября 2019.
- ^ Мьюис и Вагнер 2012, п. 19.
- ^ Стритер, Уайли и Бедфорд 1998.
- ^ Холман 2002.
- ^ Incropera et al. 2007 г..
- ^ Nič et al. 1997 г..
- ^ а б c Бёрд, Стюарт и Лайтфут 2007, п. 19.
- ^ а б Ландау и Лифшиц, 1987 г. С. 44–45.
- ^ Бёрд, Стюарт и Лайтфут 2007, п. 18: Обратите внимание, что в этом источнике используется альтернативное соглашение о знаках, которое здесь было отменено.
- ^ Ландау и Лифшиц 1987, п. 45.
- ^ а б c d е Бёрд, Стюарт и Лайтфут 2007.
- ^ Шредер 1999.
- ^ Różańska et al. 2014 г. С. 47–55.
- ^ Траутон 1906 С. 426–440.
- ^ Мьюис и Вагнер 2012 С. 228–230.
- ^ Кумагаи, Сасадзима и Ито 1978 С. 157–161.
- ^ Шерер, Парденек и Святек 1988, п. 14.
- ^ Ханнан, Генри (2007). Справочник специалиста по составу промышленных и бытовых чистящих средств. Ваукеша, Висконсин: Kyral LLC. п. 7. ISBN 978-0-6151-5601-9.
- ^ «Наноразмерная вязкость цитоплазмы сохраняется в линиях клеток человека». Дои:10.1021 / acs.jpclett.0c01748. Цитировать журнал требует
| журнал =(помощь) - ^ Макнот и Уилкинсон 1997, равновесие.
- ^ Гилленбок 2018, п. 213.
- ^ ASTM D2161: Стандартная практика преобразования кинематической вязкости в универсальную вязкость по Сейболту или в вязкость по Сейболту-фуролу, ASTM, 2005, с. 1
- ^ Эванс и Моррис 1988, стр. 4142–4148.
- ^ а б c Чепмен и Коулинг 1970.
- ^ а б Bellac, Mortessagne и Batrouni 2004.
- ^ Чепмен и Коулинг 1970, п. 103.
- ^ Черчиньяни 1975.
- ^ Сазерленд 1893 С. 507–531.
- ^ Бёрд, Стюарт и Лайтфут 2007 С. 25–27.
- ^ Чепмен и Коулинг 1970 С. 235–237.
- ^ Чепмен и Коулинг 1970, стр. 197, 214–216.
- ^ Крамер 2012, п. 066102-2.
- ^ Рид и Шервуд 1958, п. 202.
- ^ а б c Бёрд, Стюарт и Лайтфут 2007 С. 29–31.
- ^ Рид и Шервуд 1958 С. 203–204.
- ^ Хильдебранд 1958.
- ^ Хильдебранд 1958, п. 37.
- ^ Эгельстафф 1992, п. 264.
- ^ Ирвинг и Кирквуд 1949 С. 817–829.
- ^ Рид и Шервуд 1958 С. 206–209.
- ^ а б Жмуд 2014, п. 22.
- ^ а б Viswanath et al. 2007 г..
- ^ Абдулагатов, Зейналова и Азизов 2006 С. 75–88.
- ^ а б Бёрд, Стюарт и Лайтфут 2007 С. 31–33.
- ^ Бёрд, Стюарт и Лайтфут 2007, п. 32.
- ^ а б Мюллер, Ллевеллин и Мадер 2009 С. 1201–1228.
- ^ Бёрд, Стюарт и Лайтфут 2007, п. 33.
- ^ Флюгель 2007.
- ^ Doremus 2002 С. 7619–7629.
- ^ а б Охован, Трэвис и Хэнд 2007, п. 415107.
- ^ Охован и Ли 2004 С. 3803–3810.
- ^ Дайр, Олсен и Кристенсен, 1996 г., п. 2171.
- ^ а б Крауссер, Самвер и Закконе 2015, п. 13762.
- ^ Бёрд, Стюарт и Лайтфут 2007, п. 163.
- ^ Lesieur 2012, стр. 2–.
- ^ Сивашинский и Яхот 1985, п. 1040.
- ^ Се и Левченко 2019, п. 045434.
- ^ а б c d Эджворт, Далтон и Парнелл 1984 С. 198–200.
- ^ а б c d е Битва 2018.
- ^ Вишванатх и Натараджан 1989 С. 714–715.
- ^ tec-science (25.03.2020). «Вязкость жидкостей и газов». наука. Получено 2020-05-07.
- ^ а б c d Стипендиаты 2009 г..
- ^ Севера и Лос 2008.
- ^ Янниотис, Скальци и Карабурниоти 2006 С. 372–377.
- ^ а б Коочеки и др. 2009 г. С. 596–602.
- ^ а б Ситерн, Карро и Стон 2001 С. 86–96.
- ^ Кестин, Халифа и Уэйкхэм 1977 г..
- ^ Assael et al. 2018 г..
- ^ Кестин, Ро и Уэйкхэм, 1972 г..
- ^ https://web.archive.org/web/20070611192838/http://www.igw.uni-jena.de/geodyn/poster2.html
Источники
- Абдулагатов, Ильмутдин М .; Зейналова, Аделя Б .; Азизов, Назим Д. (2006). «Экспериментальные B-коэффициенты вязкости водных растворов LiCl». Журнал молекулярных жидкостей. 126 (1–3): 75–88. Дои:10.1016 / j.molliq.2005.10.006. ISSN 0167-7322.CS1 maint: ref = harv (связь)
- Assael, M. J .; и другие. (2018). «Справочные значения и справочные корреляции для теплопроводности и вязкости жидкостей». Журнал физических и химических справочных данных. 47 (2): 021501. Bibcode:2018JPCRD..47b1501A. Дои:10.1063/1.5036625. ISSN 0047-2689. ЧВК 6463310. PMID 30996494.CS1 maint: ref = harv (связь)
- Балеску, Раду (1975). Равновесная и неравновесная статистическая механика. Джон Вили и сыновья. ISBN 978-0-471-04600-4.CS1 maint: ref = harv (связь)
- Беллак, Майкл; Мортезанье, Фабрис; Батруни, Дж. Джордж (2004). Равновесная и неравновесная статистическая термодинамика. Издательство Кембриджского университета. ISBN 978-0-521-82143-8.CS1 maint: ref = harv (связь)
- Берд, Р. Байрон; Стюарт, Уоррен Э .; Лайтфут, Эдвин Н. (2007). Транспортные явления (2-е изд.). John Wiley & Sons, Inc. ISBN 978-0-470-11539-8.
- Берд, Р. Брайон; Армстронг, Роберт С .; Хассагер, Оле (1987), Динамика полимерных жидкостей, Том 1: Механика жидкости (2-е изд.), John Wiley & Sons
- Черчиньяни, Карло (1975). Теория и применение уравнения Больцмана.. Эльзевир. ISBN 978-0-444-19450-3.CS1 maint: ref = harv (связь)
- Чепмен, Сидней; Каулинг, Т. (1970). Математическая теория неоднородных газов. (3-е изд.). Издательство Кембриджского университета.CS1 maint: ref = harv (связь)
- Citerne, Guillaume P .; Карро, Пьер Дж .; Стон, Мишель (2001). «Реологические свойства арахисового масла». Rheologica Acta. 40 (1): 86–96. Дои:10.1007 / s003970000120.CS1 maint: ref = harv (связь)
- Крамер, М. (2012). «Численные оценки объемной вязкости идеальных газов». Физика жидкостей. 24 (6): 066102–066102–23. Bibcode:2012ФФЛ ... 24Ф6102С. Дои:10.1063/1.4729611. HDL:10919/47646.CS1 maint: ref = harv (связь)
- Дормус, Р.Х. (2002). «Вязкость кремнезема». J. Appl. Phys. 92 (12): 7619–7629. Bibcode:2002JAP .... 92.7619D. Дои:10.1063/1.1515132.CS1 maint: ref = harv (связь)
- Dyre, J.C .; Olsen, N.B .; Кристенсен, Т. (1996). «Модель локального упругого расширения для энергий активации вязкого течения стеклообразующих молекулярных жидкостей». Физический обзор B. 53 (5): 2171. Дои:10.1103 / PhysRevB.53.2171.CS1 maint: ref = harv (связь)
- Edgeworth, R .; Dalton, B.J .; Парнелл, Т. (1984). «Эксперимент с падением высоты звука». Европейский журнал физики. 5 (4): 198–200. Bibcode:1984EJPh .... 5..198E. Дои:10.1088/0143-0807/5/4/003. Получено 2009-03-31.CS1 maint: ref = harv (связь)
- Эгельстафф, П. А. (1992). Введение в жидкое состояние (2-е изд.). Издательство Оксфордского университета. ISBN 978-0-19-851012-3.CS1 maint: ref = harv (связь)
- Эванс, Денис Дж .; Моррис, Гэри П. (15 октября 1988 г.). «Переходно-временные корреляционные функции и реология жидкостей». Физический обзор A. 38 (8): 4142–4148. Bibcode:1988PhRvA..38.4142E. Дои:10.1103 / PhysRevA.38.4142. PMID 9900865.CS1 maint: ref = harv (связь)
- Стипендиаты, П. Дж. (2009). Технология пищевой промышленности: принципы и практика (3-е изд.). Вудхед. ISBN 978-1845692162.CS1 maint: ref = harv (связь)
- Флюгель, Александр (2007). «Расчет вязкости стекол». Glassproperties.com. Получено 2010-09-14.
- Гиббс, Филип (январь 1997 г.). "Стекло жидкое или твердое?". math.ucr.edu. Получено 19 сентября 2019.CS1 maint: ref = harv (связь)
- Гилленбок, Ян (2018). «Энциклопедия исторической метрологии, весов и мер». Энциклопедия исторической метрологии, весов и мер. Том 1. Биркхойзер. ISBN 9783319575988.CS1 maint: ref = harv (связь)
- Хильдебранд, Джоэл Генри (1977). Вязкость и диффузность: прогнозирование. Джон Вили и сыновья. ISBN 978-0-471-03072-0.CS1 maint: ref = harv (связь)
- Холман, Джек Филип (2002). Теплопередача. Макгроу-Хилл. ISBN 978-0-07-112230-6.CS1 maint: ref = harv (связь)
- Incropera, Франк П .; и другие. (2007). Основы тепломассообмена. Вайли. ISBN 978-0-471-45728-2.CS1 maint: ref = harv (связь)
- Irving, J.H .; Кирквуд, Джон Г. (1949). "Статистическая механическая теория транспортных процессов. IV. Уравнения гидродинамики". J. Chem. Phys. 18 (6): 817–829. Дои:10.1063/1.1747782.CS1 maint: ref = harv (связь)
- Kestin, J .; Ro, S.T .; Уэйкхэм, У. А. (1972). «Вязкость благородных газов в интервале температур 25–700 ° С». Журнал химической физики. 56 (8): 4119–4124. Bibcode:1972ЖЧФ..56.4119К. Дои:10.1063/1.1677824. ISSN 0021-9606.CS1 maint: ref = harv (связь)
- Kestin, J .; Khalifa, H.E .; Уэйкхэм, W.A. (1977). «Вязкость пяти газообразных углеводородов». Журнал химической физики. 66 (3): 1132. Bibcode:1977ЖЧФ..66.1132К. Дои:10.1063/1.434048.CS1 maint: ref = harv (связь)
- Коочеки, Араш; и другие. (2009). «Реологические свойства кетчупа в зависимости от различных гидроколлоидов и температуры». Международный журнал пищевой науки и технологий. 44 (3): 596–602. Дои:10.1111 / j.1365-2621.2008.01868.x.CS1 maint: ref = harv (связь)
- Krausser, J .; Samwer, K .; Закконе, А. (2015). «Мягкость межатомного отталкивания напрямую контролирует хрупкость переохлажденных металлических расплавов». Труды Национальной академии наук США. 112 (45): 13762. Дои:10.1073 / pnas.1503741112.CS1 maint: ref = harv (связь)
- Кумагаи, Наоичи; Сасадзима, Садао; Ито, Хидебуми (15 февраля 1978 г.). «Долговременная ползучесть горных пород: результаты с крупными образцами, полученными примерно за 20 лет, и с небольшими образцами примерно за 3 года». Журнал Общества материаловедения (Япония). 27 (293): 157–161. NAID 110002299397. Получено 2008-06-16.CS1 maint: ref = harv (связь)
- Ландау, Л. Д .; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN 978-0-08-057073-0.CS1 maint: ref = harv (связь)
- Лезье, Марсель (2012). Турбулентность в жидкостях: стохастическое и численное моделирование. Springer. ISBN 978-94-009-0533-7.CS1 maint: ref = harv (связь)
- Мьюис, Ян; Вагнер, Норман Дж. (2012). Реология коллоидной суспензии. Издательство Кембриджского университета. ISBN 978-0-521-51599-3.CS1 maint: ref = harv (связь)
- McNaught, A.D .; Уилкинсон, А. (1997). "равновесие". ИЮПАК. Сборник химической терминологии («Золотая книга»). С. Дж. Мел (2-е изд.). Оксфорд: Blackwell Scientific. Дои:10.1351 / goldbook. ISBN 0-9678550-9-8.CS1 maint: ref = harv (связь)
- Мюллер, С .; Llewellin, E.W .; Мадер, Х. М. (2009). «Реология суспензий твердых частиц». Труды Королевского общества A: математические, физические и инженерные науки. 466 (2116): 1201–1228. Дои:10.1098 / rspa.2009.0445. ISSN 1364-5021.CS1 maint: ref = harv (связь)
- Нич, Милослав; и др., ред. (1997). "динамическая вязкость, η". Сборник химической терминологии ИЮПАК. Оксфорд: Научные публикации Блэквелла. Дои:10.1351 / goldbook. ISBN 978-0-9678550-9-7.CS1 maint: ref = harv (связь)
- Ojovan, M.I .; Ли, W.E. (2004). «Вязкость сетевых жидкостей в рамках подхода Доремуса». J. Appl. Phys. 95 (7): 3803–3810. Bibcode:2004JAP .... 95.3803O. Дои:10.1063/1.1647260.CS1 maint: ref = harv (связь)
- Ojovan, M.I .; Travis, K. P .; Хэнд, Р.Дж. (2000). «Термодинамические параметры связей в стеклообразных материалах из зависимости вязкости от температуры» (PDF). J. Phys .: Condens. Иметь значение. 19 (41): 415107. Bibcode:2007JPCM ... 19O5107O. Дои:10.1088/0953-8984/19/41/415107. PMID 28192319.CS1 maint: ref = harv (связь)
- Пламб, Роберт С. (1989). «Старинные оконные стекла и поток переохлажденных жидкостей». Журнал химического образования. 66 (12): 994. Bibcode:1989JChEd..66..994P. Дои:10.1021 / ed066p994.CS1 maint: ref = harv (связь)
- Рид, Роберт С .; Шервуд, Томас К. (1958). Свойства газов и жидкостей. Макгроу-Хилл.CS1 maint: ref = harv (связь)
- Рейф, Ф. (1965), Основы статистической и теплофизики, Макгроу-Хилл. Современное лечение.
- Różańska, S .; Róański, J .; Ochowiak, M .; Митковски, П. Т. (2014). «Измерение расширенной вязкости концентрированных эмульсий с использованием устройства с противоположными соплами» (PDF). Бразильский журнал химической инженерии. 31 (1): 47–55. Дои:10.1590 / S0104-66322014000100006. ISSN 0104-6632.CS1 maint: ref = harv (связь)
- Рамбл, Джон Р., изд. (2018). CRC Справочник по химии и физике (99-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1138561632.CS1 maint: ref = harv (связь)
- Шерер, Джордж В .; Pardenek, Sandra A .; Святек, Роуз М. (1988). «Вязкоупругость в силикагеле». Журнал некристаллических твердых тел. 107 (1): 14. Bibcode:1988JNCS..107 ... 14S. Дои:10.1016/0022-3093(88)90086-5.CS1 maint: ref = harv (связь)
- Шредер, Дэниел В. (1999). Введение в теплофизику. Эддисон Уэсли. ISBN 978-0-201-38027-9.CS1 maint: ref = harv (связь)
- Сивашинский, В .; Яхот, Г. (1985). «Эффект отрицательной вязкости в крупномасштабных потоках». Физика жидкостей. 28 (4): 1040. Bibcode:1985ФФл ... 28.1040С. Дои:10.1063/1.865025.CS1 maint: ref = harv (связь)
- Стритер, Виктор Лайл; Уайли, Э. Бенджамин; Бедфорд, Кейт В. (1998). Механика жидкости. WCB / Макгроу Хилл. ISBN 978-0-07-062537-2.CS1 maint: ref = harv (связь)
- Сазерленд, Уильям (1893). «ЛИИ. Вязкость газов и молекулярная сила» (PDF). Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. 36 (223): 507–531. Дои:10.1080/14786449308620508. ISSN 1941-5982.CS1 maint: ref = harv (связь)
- Саймон, Кейт Р. (1971). Механика (3-е изд.). Эддисон-Уэсли. ISBN 978-0-201-07392-8.CS1 maint: ref = harv (связь)
- Траутон, Фред. Т. (1906). «О коэффициенте вязкой тяги и его связи с вязкостью». Труды Королевского общества A: математические, физические и инженерные науки. 77 (519): 426–440. Bibcode:1906RSPSA..77..426T. Дои:10.1098 / rspa.1906.0038. ISSN 1364-5021.
- Viswanath, D.S .; Натараджан, Г. (1989). Справочник по вязкости жидкостей. Издательство Hemisphere Publishing Corporation. ISBN 0-89116-778-1.CS1 maint: ref = harv (связь)
- Viswanath, Dabir S .; и другие. (2007). Вязкость жидкостей: теория, оценка, эксперимент и данные. Springer. ISBN 978-1-4020-5481-5.CS1 maint: ref = harv (связь)
- Се, Хун-И; Левченко, Алексей (23 января 2019). «Отрицательная вязкость и вихревое течение несбалансированной электронно-дырочной жидкости в графене». Phys. Ред. B. 99 (4): 045434. arXiv:1807.04770v2. Дои:10.1103 / PhysRevB.99.045434.CS1 maint: ref = harv (связь)
- Yanniotis, S .; Скальци, С .; Карабурниоти, С. (февраль 2006 г.). «Влияние влажности на вязкость меда при разных температурах». Журнал пищевой инженерии. 72 (4): 372–377. Дои:10.1016 / j.jfoodeng.2004.12.017.CS1 maint: ref = harv (связь)
- Жмуд, Борис (2014). «Уравнения смешения вязкости» (PDF). Lube-Tech: 93. Смазка. № 121. С. 22–27.CS1 maint: ref = harv (связь)
внешняя ссылка
- Свойства жидкости - высокоточный расчет вязкости для часто встречающихся чистых жидкостей и газов
- Калькулятор вязкости газа как функция температуры
- Калькулятор вязкости воздуха как функция температуры и давления
- Таблица характеристик жидкости - таблица вязкости и давления пара для различных жидкостей
- Набор инструментов для газовой динамики - рассчитывать коэффициент вязкости для смесей газов
- Измерение вязкости стекла - измерение вязкости, единицы вязкости и точки фиксации, расчет вязкости стекла
- Кинематическая вязкость - преобразование кинематической вязкости в динамическую
- Физические характеристики воды - таблица вязкости воды в зависимости от температуры
- Параметры уравнения Фогеля – Таммана – Фулчера.
- Расчет динамической вязкости в зависимости от температуры для некоторых общих компонентов
- «Процедуры испытаний для испытаний автомобильных и внедорожных двигателей и всесторонние технические поправки» – Агентство по охране окружающей среды США
- Искусственная вязкость
- Вязкость воздуха, динамика и кинематика, Engineers Edge



























![{ displaystyle mathbf { tau} = mu left [ nabla mathbf {v} + ( nabla mathbf {v}) ^ { dagger} right] - left ({ frac {2}) {3}} mu - kappa right) ( nabla cdot mathbf {v}) mathbf { delta},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a3d8d9a7b9d48854ded27cabf22577676ee9188)







![{ displaystyle { begin {align} mathbf {J} & = - D { frac { partial rho} { partial x}} && { text {(закон диффузии Фика)}} [5pt ] mathbf {q} & = - k_ {t} { frac { partial T} { partial x}} && { text {(Закон теплопроводности Фурье)}} [5pt] tau & = mu { frac { partial u} { partial y}} && { text {(закон вязкости Ньютона)}} end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6380b89b0d24d9c9deb9ef04f333430b073c45cc)

































































![{ displaystyle mu = AT exp left ({ frac {B} {RT}} right) left [1 + C exp left ({ frac {D} {RT}} right) верно],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38aa9224e9ac73624655cd20405e140af63a62eb)
![{ displaystyle mu = exp { left {{ frac {V_ {c} C_ {G}} {k_ {B} T}} exp { left [(2+ lambda) alpha _ { T} T_ {g} left (1 - { frac {T} {T_ {g}}} right) right]} right }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c6670713177337446c22a7976e9664d2008526)








