Пластичность (физика) - Plasticity (physics)

Кривая напряжение – деформация показывая типичный урожай поведение для цветные сплавы. (Стресс, ${ displaystyle sigma}$, показанный как функция напряжение, ${ displaystyle epsilon}$.)

1. Истинный предел упругости
2. Предел пропорциональности
3. Предел упругости
4. Компенсировать предел текучести

А кривая напряжение – деформация типично конструкционная сталь.

---

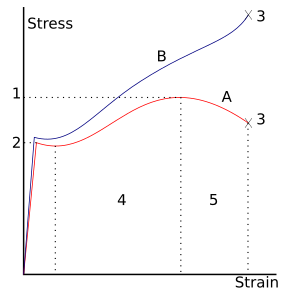
• 1: Невероятная сила
• 2: Предел текучести (предел текучести)
• 3: Разрыв
• 4: Деформационное упрочнение область, край
• 5: Шейный область, край
• A: Видимое напряжение (F/А₀)
• B: Фактическое напряжение (F/А)

В физика и материаловедение, пластичность, также известный как Пластическая деформация, это способность твердого материала подвергаться постоянному деформация, необратимое изменение формы под действием приложенных сил.^[1][2] Например, твердый кусок металла, который сгибается или прижимается к новой форме, демонстрирует пластичность, поскольку в самом материале происходят постоянные изменения. В инженерии переход от эластичный поведение к пластическому поведению известно как уступающий.

Пластическая деформация наблюдается у большинства материалов, особенно у металлы, почвы, горные породы, конкретный, пены.^[3][4][5][6] Однако физические механизмы, вызывающие пластическую деформацию, могут широко варьироваться. На кристаллический окалины, пластичность металлов обычно является следствием вывихи. Такие дефекты относительно редки в большинстве кристаллических материалов, но многочисленны в некоторых частях их кристаллической структуры; в таких случаях, пластическая кристалличность может привести. В хрупких материалах, таких как скала, бетон и кость, пластичность в основном обусловлена соскальзывать в микротрещины. В ячеистых материалах, таких как жидкость пены или же биологические ткани, пластичность в основном является следствием перестройки пузырьков или клеток, особенно T1 процессы.

Для многих пластичный металлы, растягивающая нагрузка нанесение на образец приведет к его эластичному поведению. Каждое увеличение нагрузки сопровождается пропорциональным увеличением растяжения. Когда груз снимается, деталь возвращается к своему первоначальному размеру. Однако как только нагрузка превышает пороговое значение - предел текучести - растяжение увеличивается быстрее, чем в упругой области; теперь, когда нагрузка снята, некоторая степень расширения останется.

Упругая деформация Однако это приблизительное значение, и его качество зависит от рассматриваемого периода времени и скорости загрузки. Если, как показано на графике напротив, деформация включает в себя упругую деформацию, ее также часто называют «упругопластической деформацией» или «упруго-пластической деформацией».

Совершенная пластичность - это свойство материалов необратимо деформироваться без увеличения напряжений или нагрузок. Пластиковые материалы, которые были закаленный предшествующей деформацией, такой как холодное формование, для дальнейшей деформации могут потребоваться все более высокие напряжения. Как правило, пластическая деформация также зависит от скорости деформации, т.е. для увеличения скорости деформации обычно должны применяться более высокие напряжения. Считается, что такие материалы деформируют вязкопластически.

Внесение свойств

Пластичность материала прямо пропорциональна пластичность и пластичность материала.

Физические механизмы

Пластичность под сферическим наноиндентором в меди (111). Все частицы в идеальных положениях решетки опущены, а цветовой код относится к полю напряжений фон Мизеса.

В металлах

Пластичность кристалла чистого металла в первую очередь обусловлена ​​двумя режимами деформации кристаллической решетки: скольжением и двойникованием. Скольжение - это деформация сдвига, которая перемещает атомы на многие межатомные расстояния относительно их начального положения. Двойникование - это пластическая деформация, которая происходит в двух плоскостях из-за набора сил, приложенных к данной металлической детали.

Большинство металлов в горячем состоянии более пластичны, чем в холодном состоянии. Свинец показывает достаточную пластичность при комнатной температуре, в то время как чугун не обладает достаточной пластичностью для любых операций ковки, даже в горячем состоянии. Это свойство важно при операциях формования, формования и экструзии металлов. Большинство металлов превращаются в пластичные при нагревании и, следовательно, в горячем состоянии.

Системы скольжения

Кристаллические материалы содержат однородные плоскости атомов, организованные с дальним порядком. Самолеты могут скользить мимо друг друга в своих плотно упакованных направлениях, как показано на странице систем скольжения. В результате происходит постоянное изменение формы кристалла и пластическая деформация. Наличие дислокаций увеличивает вероятность появления плоскостей.

Обратимая пластичность

В наномасштабе первичная пластическая деформация в простом виде гранецентрированная кубическая металлы обратимы, пока нет переноса материала в виде поперечное скольжение.^[7]

Полосатость сдвига

Наличие других дефектов внутри кристалла может запутывать дислокации или иным образом препятствовать их скольжению. Когда это происходит, пластичность локализуется в определенных областях материала. Для кристаллов эти области локализованной пластичности называют полосы сдвига.

Микропластичность

Микропластичность - это локальное явление в металлах. Это происходит для стресс значения, где металл находится в глобальном эластичный домен, в то время как некоторые области находятся в области пластика.^[8]

Аморфные материалы

Сумасшествие

В аморфный материалов обсуждение «дислокаций» неприменимо, так как весь материал лишен дальнего порядка. Эти материалы все еще могут подвергаться пластической деформации. Поскольку аморфные материалы, такие как полимеры, неупорядочены, они содержат большое количество свободного объема или бесполезного пространства. Вытягивание этих материалов с натяжением открывает эти области и может придать материалам мутный вид. Эта нечеткость - результат трескаться, куда фибриллы образуются внутри материала в областях высоких гидростатическое напряжение. Внешний вид материала может измениться от упорядоченного до «сумасшедшего» рисунка растяжек и растяжек.

Ячеистые материалы

Эти материалы пластически деформируются, когда изгибающий момент превышает полностью пластический момент. Это относится к пенопластам с открытыми ячейками, где изгибающий момент действует на стенки ячеек. Пенопласт может быть изготовлен из любого материала с пределом пластической текучести, включая жесткие полимеры и металлы. Этот метод моделирования пены в виде балок действителен только в том случае, если отношение плотности пены к плотности вещества меньше 0,3. Это связано с тем, что балки изгибаются в осевом направлении, а не изгибаются. В пенопластах с закрытыми ячейками предел текучести увеличивается, если материал находится под напряжением из-за мембраны, которая охватывает поверхность ячеек.

Почвы и песок

Грунты, особенно глины, проявляют значительную неупругость под нагрузкой. Причины пластичности почв могут быть довольно сложными и сильно зависят от микроструктура, химический состав и содержание воды. Пластичность почв обусловлена ​​в первую очередь перестройкой скоплений соседних зерен.

Камни и бетон

Неупругие деформации горных пород и бетона в первую очередь вызваны образованием микротрещин и скользящими движениями относительно этих трещин. При высоких температурах и давлениях на пластическое поведение также может влиять движение дислокаций в отдельных зернах микроструктуры.

Математические описания

Теория деформации

Идеализированный одноосный кривая напряжения-деформации показаны режимы упругого и пластического деформирования для теории деформации пластичности.

Есть несколько математических описаний пластичности.^[9] Один из них - теория деформации (см., Например, Закон Гука ) где Тензор напряжений Коши (порядка d-1 в d измерениях) является функцией тензора деформации. Хотя это описание является точным, когда небольшая часть вещества подвергается возрастающей нагрузке (например, деформационной нагрузке), эта теория не может объяснить необратимость.

Пластичные материалы могут выдерживать большие пластические деформации без перелом. Однако даже пластичные металлы будут разрушаться, когда напряжение становится достаточно большим - это в результате упрочнение материала, из-за чего он становится хрупкий. Термическая обработка Такие как отжиг может восстановить пластичность обработанной детали, чтобы можно было продолжить формирование.

Теория пластичности течения

В 1934 г. Эгон Орован, Майкл Поланьи и Джеффри Ингрэм Тейлор, примерно одновременно, понял, что пластическая деформация пластичных материалов может быть объяснена с точки зрения теории вывихи. Математическая теория пластичности, теория пластичности потока, использует набор нелинейных, неинтегрируемых уравнений для описания набора изменений деформации и напряжения по сравнению с предыдущим состоянием и небольшого увеличения деформации.

Критерии доходности

Сравнение критерия Трески с критерием фон Мизеса

Если напряжение превышает критическое значение, как было сказано выше, материал подвергнется пластической или необратимой деформации. Это критическое напряжение может быть растягивающим или сжимающим. Треска и фон Мизес критерии обычно используются для определения текучести материала. Однако эти критерии оказались недостаточными для большого диапазона материалов, и некоторые другие критерии текучести также широко используются.

Критерий Трески

Критерий Трески основан на представлении о том, что, когда материал выходит из строя, это происходит при сдвиге, что является относительно хорошим предположением при рассмотрении металлов. Учитывая главное напряженное состояние, мы можем использовать Круг Мора для определения максимальных касательных напряжений, которые наш материал испытает и сделает вывод, что материал выйдет из строя, если

${ displaystyle sigma _ {1} - sigma _ {3} geq sigma _ {0}}$

куда σ₁ это максимальное нормальное напряжение, σ₃ - минимальное нормальное напряжение, а σ₀ - это напряжение, при котором материал разрушается при одноосной нагрузке. А поверхность текучести могут быть построены, что обеспечивает визуальное представление этой концепции. Внутри поверхности текучести деформация упругая. На поверхности деформация пластическая. Материал не может иметь напряженное состояние за пределами своей поверхности текучести.

Критерий Губера – фон Мизеса

Поверхность текучести фон Мизеса в координатах главных напряжений описывает цилиндр вокруг гидростатической оси. Также показано Треска гексагональная поверхность текучести.

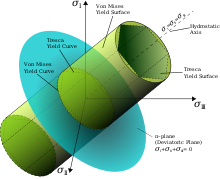
Критерий Губера – фон Мизеса^[10] основан на критерии Трески, но принимает во внимание предположение, что гидростатические напряжения не способствуют разрушению материала. М. Т. Хубер был первым, кто предложил критерий энергии сдвига.^[11][12] Фон Мизес решает эффективный стресс при одноосном нагружении, вычитая гидростатические напряжения, и заявляет, что все эффективные напряжения, превышающие то, которое вызывает разрушение материала при одноосном нагружении, приведут к пластической деформации.

${ displaystyle sigma _ {v} ^ {2} = { tfrac {1} {2}} [( sigma _ {11} - sigma _ {22}) ^ {2} + ( sigma _ { 22} - sigma _ {33}) ^ {2} + ( sigma _ {11} - sigma _ {33}) ^ {2} +6 ( sigma _ {23} ^ {2} + sigma _ {31} ^ {2} + sigma _ {12} ^ {2})]}$

Опять же, визуальное представление поверхности текучести может быть построено с использованием приведенного выше уравнения, которое принимает форму эллипса. Внутри поверхности материалы подвергаются упругой деформации. Достижение поверхности означает, что материал подвергается пластической деформации.

Смотрите также

• Пределы Аттерберга
• Пластометр
• Коэффициент Пуассона

Рекомендации

дальнейшее чтение

• Эшби, М.Ф. (2001). «Пластическая деформация ячеистых материалов». Энциклопедия материалов: наука и технологии. Том 7. Оксфорд: Elsevier. С. 7068–7071. ISBN  0-08-043152-6.
• Han, W .; Редди, Б. Д. (2013). Пластичность: математическая теория и численный анализ (2-е изд.). Нью-Йорк: Спрингер. ISBN  978-1-4614-5939-2.
• Качанов, Л. М. (2004). Основы теории пластичности. Dover Книги. ISBN  0-486-43583-0.
• Хан, А. С .; Хуанг, С. (1995). Континуальная теория пластичности. Вайли. ISBN  0-471-31043-3.
• Simo, J.C .; Хьюз, Т. Дж. (1998). Вычислительная неупругость. Springer. ISBN  0-387-97520-9.
• Ван Влит, К. Дж. (2006). «Механическое поведение материалов». Номер курса MIT 3.032. Массачусетский Институт Технологий.