Механика критического состояния грунтов - Critical state soil mechanics

Нормально уплотненный грунт переходит в критическое состояние по пути напряжений на поверхности Роско.

Механика критических состояний грунтов это площадь механика грунта который включает концептуальные модели, которые представляют механическое поведение насыщенных переформованных грунтов на основе Критическое состояние концепция.

Формулировка

Концепция критического состояния представляет собой идеализацию наблюдаемого поведения насыщенных переформованных глин в испытания на трехосное сжатие, и предполагается, что он применяется к ненарушенным почвам. В нем говорится, что грунт и другие зернистые материалы, если они непрерывно деформируются (раскалываются) до тех пор, пока они не текут как фрикционная жидкость, придут в четко определенное критическое состояние. В начале критического состояния сдвиговые искажения ${displaystyle varepsilon _ {s}}$ происходят без дальнейших изменений среднего эффективного напряжения ${displaystyle p '}$, девиаторное напряжение ${displaystyle q}$ (или предел текучести, ${displaystyle sigma _ {y}}$, при одноосном растяжении по критерий уступки фон Мизеса ) или удельный объем ${displaystyle u}$:

${displaystyle {frac {partial p '} {partial varepsilon _ {s}}} = {frac {partial q} {partial varepsilon _ {s}}} = {frac {partial u} {partial varepsilon _ {s}}} = 0}$

куда,

${displaystyle u = 1 + e}$

${displaystyle p '= {frac {1} {3}} (sigma _ {1}' + sigma _ {2} '+ sigma _ {3}')}$

${displaystyle q = {sqrt {frac {(sigma _ {1} '- sigma _ {2}') ^ {2} + (sigma _ {2} '- sigma _ {3}') ^ {2} + ( сигма _ {1} '- сигма _ {3}') ^ {2}} {2}}}}$

Однако для трехосных условий ${displaystyle sigma _ {2} '= sigma _ {3}'}$. Таким образом,

${displaystyle p '= {frac {1} {3}} (sigma _ {1}' + 2sigma _ {3} ')}$

${displaystyle q = (sigma _ {1} '- sigma _ {3}')}$

Все критические состояния для данного грунта образуют уникальную линию, называемую Критическая линия состояния (CSL), определяемые следующими уравнениями в пространстве ${displaystyle (p ', q, v)}$:

${displaystyle q = Mp '}$

${displaystyle u = Gamma -lambda ln (p ')}$

куда ${displaystyle M}$, ${displaystyle Gamma}$, и ${displaystyle lambda}$ - почвенные константы. Первое уравнение определяет величину девиаторного напряжения ${displaystyle q}$ необходим для поддержания непрерывного движения почвы как результат постоянной трения ${displaystyle M}$ (капитал ${displaystyle mu}$) и среднее эффективное напряжение ${displaystyle p '}$. Второе уравнение утверждает, что удельный объем ${displaystyle u}$ занимаемая единицей объема текущих частиц будет уменьшаться по мере увеличения логарифма среднего эффективного напряжения.

История

В попытке усовершенствовать методы тестирования почвы, Кеннет Гарри Роско из Кембриджский университет в конце сороковых - начале пятидесятых годов разработал простой сдвигающий аппарат, в котором его последовательные ученики пытались изучить изменения условий в зоне сдвига как в песках, так и в глинистых почвах. В 1958 г. было проведено исследование текучести грунта, основанное на некоторых кембриджских данных испытаний простых устройств сдвига и на гораздо более обширных данных трехосных испытаний при Имперский колледж Лондон из исследования под руководством профессора сэра Алек Скемптон на Императорские геотехнические лаборатории, привело к публикации концепции критического состояния (Роско, Шофилд и Рот, 1958 г. ).

Роско получил степень бакалавра в области машиностроения.^[1] его опыт создания туннелей для побега, когда он был военнопленным нацистами во время Второй мировой войны, познакомил его с механикой почвы.^[1] Вслед за этой статьей 1958 года концепции пластичности были введены Шофилдом и опубликованы классическим учебником (Шофилд и Гнев 1968 ). Шофилд учился в Кембридже у Проф. Джон Бейкер, инженер-строитель, твердо веривший в создание конструкций, которые не выдержат «пластического» отказа. Теории профессора Бейкера сильно повлияли на размышления Шофилда о сдвиге почвы. Взгляды профессора Бейкера были разработаны на основе его довоенных работ по стальным конструкциям и дополнительно основаны на его опыте военного времени при оценке поврежденных в результате взрыва конструкций и при проектировании «Укрытия Моррисона», бомбоубежища, которое может быть расположено в помещении (Шофилд 2006 ).

Оригинальная модель Cam-Clay

Модель Original Cam-Clay основана на предположении, что почва изотропна, эластопластична, деформируется как континуум, и на него не влияет ползучесть. В поверхность текучести модели кулачковой глины описывается уравнением

${displaystyle f (p, q, p_ {c}) = q + M, p, ln left [{frac {p} {p_ {c}}} ight] leq 0}$

куда ${displaystyle q}$ - эквивалентное напряжение, ${displaystyle p}$ давление, ${displaystyle p_ {c}}$ давление до консолидации, и ${displaystyle M}$ - наклон линии критического состояния в ${displaystyle p-q}$ Космос.

Давление предварительного уплотнения изменяется по мере увеличения пустотности (${displaystyle e}$) (и, следовательно, удельный объем ${displaystyle v}$) изменений почвы. Обычно используется соотношение

${displaystyle e = e_ {0} -lambda ln left [{frac {p_ {c}} {p_ {c0}}} ight]}$

куда ${displaystyle lambda}$ девственница индекс сжатия почвы. Ограничением этой модели является возможность отрицательных удельных объемов при реалистичных значениях напряжения.

Улучшение указанной выше модели для ${displaystyle p_ {c}}$ это билогарифмическая форма

${displaystyle ln left [{frac {1 + e} {1 + e_ {0}}} ight] = ln left [{frac {v} {v_ {0}}} ight] = - {ilde {lambda}} ln слева [{frac {p_ {c}} {p_ {c0}}} ight]}$

куда ${displaystyle {ilde {lambda}}}$ - соответствующий индекс сжимаемости почвы.

Поверхность текучести кулачка в p-q пространстве.

Поверхность текучести кулачковой глины в пространстве главных напряжений.

Модифицированная модель Cam-Clay

Профессор Джон Берланд из Имперский колледж который работал с профессором Роско, приписывают разработку модифицированной версии оригинальной модели. Разница между кулачковой глиной и модифицированной кулачковой глиной ^[2] (MCC) заключается в том, что поверхность текучести MCC описывается эллипсом, и поэтому вектор приращения пластической деформации (который перпендикулярен поверхности текучести) для наибольшего значения среднего эффективного напряжения является горизонтальным, и, следовательно, нет возрастающей девиаторной пластичности деформация имеет место при изменении среднего эффективного напряжения (для чисто гидростатических напряженных состояний). Это очень удобно для конститутивного моделирования в численном анализе, особенно анализ методом конечных элементов, где важны вопросы числовой устойчивости (поскольку кривая должна быть непрерывной, чтобы ее можно было дифференцировать).

Поверхность текучести модифицированной модели Cam-Clay имеет вид

${displaystyle f (p, q, p_ {c}) = left [{frac {q} {M}} ight] ^ {2} + p, (p-p_ {c}) leq 0}$

куда ${displaystyle p}$ давление, ${displaystyle q}$ - эквивалентное напряжение, ${displaystyle p_ {c}}$ давление до консолидации, и ${displaystyle M}$ - наклон линии критического состояния.

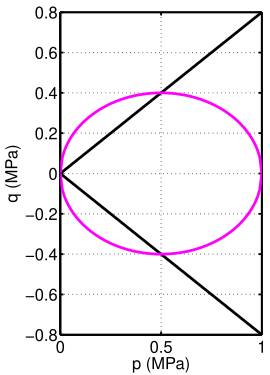Модифицированная поверхность текучести Cam-Clay в p-q пространстве.

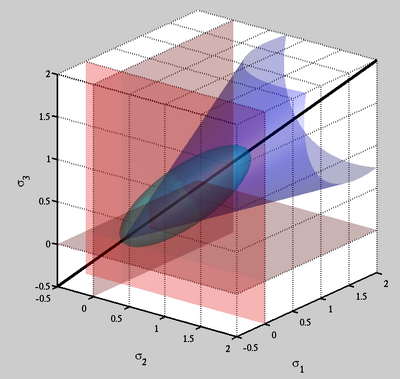Модифицированная поверхность текучести кулачковой глины в пространстве главных напряжений.

Критика

Основные концепции упругопластического подхода впервые были предложены двумя математиками. Дэниел С. Друкер и Уильям Прагер (Drucker and Prager, 1952) в короткой заметке на восьми страницах.^[3] В своей заметке Друкер и Прагер также продемонстрировали, как использовать свой подход для расчета критической высоты вертикального вала с использованием либо плоскости, либо поверхности разрушения бревенчатой ​​спирали. Их критерий доходности сегодня называется Друкер-Прагер критерий доходности. Их подход впоследствии был расширен Кеннет Х. Роско и другие на факультете механики грунтов Кембриджского университета.

Механика критического состояния и упругопластического грунта подвергалась критике с момента их появления. Ключевым фактором, вызывающим критику, является прежде всего неявное предположение, что почвы состоят из изотропных точечных частиц. Реальные почвы состоят из частиц конечного размера с анизотропными свойствами, которые во многом определяют наблюдаемое поведение. Следовательно, модели, основанные на теории пластичности, основанной на металлах, не могут моделировать поведение грунтов, которое является результатом свойств анизотропных частиц, одним из примеров которых является падение прочности на сдвиг после пика прочности, то есть поведение при деформационном разупрочнении. Из-за этого модели упругопластического грунта могут моделировать только «простые кривые зависимости напряжения от деформации», такие как кривые изотропных нормально или слегка уплотненных «жирных» глин, то есть грунтов типа CL-ML, состоящих из очень мелкозернистых частиц.

Кроме того, в целом изменение объема определяется соображениями эластичности, и, поскольку это предположение в значительной степени неверно для реальных грунтов, приводит к очень плохому согласованию этих моделей с изменениями объема или изменениями порового давления. Кроме того, эластопластические модели описывают весь элемент в целом, а не конкретные условия, непосредственно в плоскости разрушения, вследствие чего они не моделируют кривую напряжения-деформации после разрушения, особенно для грунтов, которые имеют пост-деформационное разупрочнение. вершина горы. Наконец, большинство моделей разделяют эффекты гидростатического напряжения и напряжения сдвига, при этом предполагается, что каждая из них вызывает только изменение объема и изменение сдвига соответственно. В действительности структура грунта, будучи аналогом «карточного домика», показывает как деформации сдвига при приложении чистого сжатия, так и изменения объема при применении чистого сдвига.

Дополнительные критические замечания заключаются в том, что теория является «только описательной», то есть описывает только известное поведение и не имеет возможности ни объяснить, ни предсказать стандартное поведение грунта, например, почему коэффициент пустотности в одномерном испытании на сжатие изменяется линейно с логарифмом вертикальное эффективное напряжение. Такое поведение механика грунтов считает критическим состоянием как данность.

По этим причинам механику критического состояния и упругопластическую механику грунта обвиняют в схоластике; испытания, демонстрирующие его достоверность, обычно являются «испытаниями на соответствие», когда только простые кривые напряжения-деформации демонстрируют, что моделируются удовлетворительно. Критическое состояние и окружающие его концепции имеют долгую историю «схоластики», сэр Алек Скемптон, «отец-основатель» британской механики грунтов, приписал схоластический характер CSSM Роско, о котором он сказал: «… он мало занимался полевыми работами и, я полагаю, никогда не участвовал в практических инженерных работах ».^[4]В 1960-х и 1970-х годах профессор Алан Бишоп из Имперского колледжа обычно демонстрировал неспособность этих теорий соответствовать кривым напряжения-деформации реальных грунтов. Джозеф (2013) предположил, что механика критического состояния и упругопластической механики грунта соответствует критерию «программы вырожденных исследований» - концепции, предложенной философом науки. Имре Лакатош, для теорий, где оправдания используются для оправдания неспособности теории соответствовать эмпирическим данным.^[5]

Ответ

Утверждения о том, что механика критического состояния грунта носит только описательный характер и соответствует критерию дегенеративной исследовательской программы, не решены. Эндрю Дженик использовал логарифмически-логарифмическое соотношение для описания испытания на сжатие в своей теории критического состояния и допустил уменьшение напряжения во время сходящегося потока и увеличение напряжения во время расходящегося потока.^[6] Крис Сальвински определил критическое состояние как многофазное состояние, при котором удельный объем одинаков как в твердой, так и в жидкой фазах.^[7] Согласно его определению, линейно-логарифмическое отношение исходной теории и логарифмико-логарифмическое соотношение Дженике являются частными случаями более общего физического явления.

Примечания

Рекомендации