Вязкопластичность - Viscoplasticity

Рисунок 1. Элементы, используемые в одномерных моделях вязкопластических материалов.

Вязкопластичность это теория в механика сплошной среды который описывает зависящее от скорости неупругое поведение твердых тел. Зависимость от скорости в данном контексте означает, что деформация материала зависит от скорости, с которой грузы применяются.^[1] Неупругое поведение, которое является предметом вязкопластичности, есть Пластическая деформация Это означает, что материал подвергается неустранимой деформации при достижении уровня нагрузки. Зависимая от скорости пластичность важна для расчетов переходной пластичности. Основное различие между не зависящими от скорости моделями пластических и вязкопластических материалов заключается в том, что последние не только демонстрируют остаточные деформации после приложения нагрузок, но и продолжают подвергаться постоянным деформациям. слизняк поток как функция времени под действием приложенной нагрузки.

Упругий отклик вязкопластических материалов можно одномерно представить как Hookean весна элементы. Зависимость от скорости может быть представлена ​​нелинейным приборная панель элементы аналогично вязкоупругость. Пластичность можно учесть добавлением скольжения фрикционный элементы, как показано на рисунке 1.^[2] На рисунке E - модуль упругости, λ - вязкость параметр, а N - сила закона параметр типа, представляющий нелинейный индикатор [σ (dε / dt) = σ = λ (dε / dt)^{(1 / N)}]. Скользящий элемент может иметь предел текучести (σ_у) то есть скорость деформации зависимая или даже постоянная, как показано на рисунке 1c.

Вязкопластичность обычно моделируется в трех измерениях с использованием перенапрягать модели типа Perzyna или Duvaut-Lions.^[3] В этих моделях напряжение может увеличиваться за пределы, не зависящие от скорости. поверхность текучести после приложения нагрузки, а затем позволяют расслабиться обратно на поверхность текучести с течением времени. В таких моделях обычно предполагается, что поверхность текучести не зависит от скорости. Альтернативный подход - добавить скорость деформации зависимость от предела текучести и использование методов независимой от скорости пластичности для расчета реакции материала^[4]

За металлы и сплавы, вязкопластичность - это макроскопический поведение, вызванное механизмом, связанным с движением вывихи в зерна, с наложенными эффектами межкристаллитного скольжения. Этот механизм обычно становится доминирующим при температурах, превышающих примерно одну треть от абсолютной температуры плавления. Однако некоторые сплавы проявляют вязкопластичность при комнатной температуре (300 К). За полимеры, дерево, и битум, теория вязкопластичности требуется для описания поведения за пределами упругости или вязкоупругость.

В целом теории вязкопластичности полезны в таких областях, как

• расчет остаточных деформаций,
• прогноз пластического обрушения конструкций,
• исследование устойчивости,
• моделирование аварий,
• системы, подверженные воздействию высоких температур, такие как турбины в двигателях, например электростанция,
• динамические задачи и системы, подверженные высоким скоростям деформации.

История

Исследования теорий пластичности начались в 1864 г. Анри Треска,^[5] Saint Venant (1870) и Леви (1871)^[6] на критерий максимального сдвига.^[7] Улучшенная модель пластичности была представлена ​​в 1913 г. Фон Мизес^[8] который теперь называется критерий текучести фон Мизеса. В области вязкопластичности разработка математической модели восходит к 1910 году с представлением первичная ползучесть по закону Андраде.^[9] В 1929 году Нортон^[10] разработали одномерную модель дашпота, которая связала скорость вторичная ползучесть к стрессу. В 1934 году Odqvist^[11] обобщил закон Нортона на многоосный случай.

Такие концепции, как нормальность пластического течения относительно поверхности текучести и правила течения для пластичности, были введены Прандтль (1924)^[12] и Ройсс (1930).^[13] В 1932 году Хохенемзер и Prager ^[14] предложил первую модель медленного вязкопластического течения. Эта модель обеспечила связь между девиаторное напряжение и скорость деформации для несжимаемого Бингем твердый^[15] Однако применение этих теорий началось не раньше 1950 г., когда были открыты предельные теоремы.

В 1960 г. первый IUTAM Симпозиум «Ползучесть конструкций», организованный Хоффом^[16] обеспечили серьезное развитие вязкопластичности с работами Хоффа, Работнова, Пержины, Хульта и Леметра для изотропное упрочнение законы, а также законы Краточвиля, Малинини и Хаджинского, Понтера и Леки, и Шабоша для кинематическая закалка законы. Perzyna в 1963 году ввел коэффициент вязкости, зависящий от температуры и времени.^[17] Сформулированные модели были поддержаны термодинамика из необратимые процессы и феноменологический точка зрения. Идеи, представленные в этих работах, легли в основу большинства последующих исследований пластичности, зависящей от скорости.

Феноменология

Для качественного анализа выполняется несколько характерных тестов для описания феноменологии вязкопластических материалов. Некоторые примеры этих тестов: ^[9]

1. испытания на упрочнение при постоянном напряжении или скорости деформации,
2. испытания на ползучесть при постоянной силе, и
3. снятие напряжений при постоянном удлинении.

Испытание на деформационное упрочнение

Рисунок 2. Напряжение-деформация вязкопластического материала при различных скоростях деформации. Пунктирные линии показывают реакцию, если скорость деформации остается постоянной. Синяя линия показывает реакцию при резком изменении скорости деформации.

Одно из последствий уступающий заключается в том, что при пластической деформации увеличивается стресс требуется для производства дополнительных напряжение. Это явление известно как Деформация / деформационное упрочнение.^[18] Для вязкопластического материала кривые упрочнения существенно не отличаются от кривых для не зависящего от скорости пластического материала. Тем не менее можно заметить три существенных отличия.

1. При той же деформации, чем выше скорость деформации, тем выше напряжение.
2. Изменение скорости деформации во время испытания приводит к немедленному изменению кривой напряжения-деформации.
3. Концепция предел текучести пластика больше не применимо строго.

Гипотеза разделения деформаций путем разделения упругой и пластической частей все еще применима там, где деформации небольшие,^[3] т.е.

${ displaystyle { boldsymbol { varepsilon}} = { boldsymbol { varepsilon}} _ { mathrm {e}} + { boldsymbol { varepsilon}} _ { mathrm {vp}}}$

куда ${ displaystyle { boldsymbol { varepsilon}} _ { mathrm {e}}}$ - упругая деформация и ${ displaystyle { boldsymbol { varepsilon}} _ { mathrm {vp}}}$ - вязкопластическая деформация. Чтобы получить поведение «напряжение-деформация», показанное на рисунке синим цветом, материал сначала нагружают со скоростью деформации 0,1 / с. Затем скорость деформации мгновенно повышается до 100 / с и некоторое время поддерживается постоянной на этом уровне. В конце этого периода времени скорость деформации мгновенно снижается до 0,1 / с, и цикл продолжается для увеличения значений деформации. Очевидно, что существует задержка между изменением скорости деформации и реакцией на напряжение. Это запаздывание довольно точно моделируется моделями перенапряжения (такими как Perzyna модель ), но не с помощью моделей пластичности, не зависящей от скорости, которые имеют предел текучести, зависящий от скорости.

Испытание на ползучесть

Рисунок 3а. Испытание на ползучесть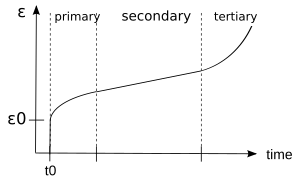

Рисунок 3b. Деформация как функция времени при испытании на ползучесть.

Слизняк это тенденция твердого материала к медленному перемещению или постоянной деформации под постоянными напряжениями. Испытания на ползучесть измеряют реакцию на деформацию из-за постоянного напряжения, как показано на рисунке 3. Классическая кривая ползучести представляет эволюцию деформации как функцию времени в материале, подвергающемся одноосному напряжению при постоянной температуре. Например, испытание на ползучесть выполняется путем приложения постоянной силы / напряжения и анализа реакции системы на деформацию. В целом, как показано на рисунке 3b, эта кривая обычно показывает три фазы или периода поведения.^[9]

1. А первичная ползучесть Стадия, также известная как переходная ползучесть, является начальной стадией, во время которой затвердевание материала приводит к снижению скорости потока, которая изначально очень высока. ${ displaystyle (0 leq { boldsymbol { varepsilon}} leq { boldsymbol { varepsilon}} _ {1})}$.
2. В вторичная ползучесть Стадия, также известная как установившееся состояние, - это когда скорость деформации постоянна. ${ displaystyle ({ boldsymbol { varepsilon}} _ {1} leq { boldsymbol { varepsilon}} leq { boldsymbol { varepsilon}} _ {2})}$.
3. А третичная ползучесть фаза, в которой происходит увеличение скорости деформации вплоть до деформации разрушения. ${ displaystyle ({ boldsymbol { varepsilon}} _ {2} leq { boldsymbol { varepsilon}} leq { boldsymbol { varepsilon}} _ {R})}$.

Тест на расслабление

Рисунок 4. а) Приложенная деформация в испытании на релаксацию и б) индуцированное напряжение как функции времени в течение короткого периода для вязкопластического материала.

Как показано на рисунке 4, релаксационный тест^[19] определяется как реакция на стресс из-за постоянной деформации в течение определенного периода времени. В вязкопластических материалах релаксационные испытания демонстрируют релаксацию напряжений при одноосном нагружении при постоянной деформации. Фактически, эти испытания характеризуют вязкость и могут использоваться для определения взаимосвязи, существующей между напряжением и скоростью вязкопластической деформации. Разложение скорости деформации:

${ displaystyle { cfrac { mathrm {d} { boldsymbol { varepsilon}}} { mathrm {d} t}} = { cfrac { mathrm {d} { boldsymbol { varepsilon}} _ { mathrm {e}}} { mathrm {d} t}} + { cfrac { mathrm {d} { boldsymbol { varepsilon}} _ { mathrm {vp}}} { mathrm {d} t }} ~.}$

Упругая часть скорости деформации определяется выражением

${ displaystyle { cfrac { mathrm {d} { boldsymbol { varepsilon}} _ { mathrm {e}}} { mathrm {d} t}} = { mathsf {E}} ^ {- 1 } ~ { cfrac { mathrm {d} { boldsymbol { sigma}}} { mathrm {d} t}}}$

Для плоского участка кривой зависимости деформации от времени полная скорость деформации равна нулю. Следовательно, мы имеем

${ displaystyle { cfrac { mathrm {d} { boldsymbol { varepsilon}} _ { mathrm {vp}}} { mathrm {d} t}} = - { mathsf {E}} ^ {- 1} ~ { cfrac { mathrm {d} { boldsymbol { sigma}}} { mathrm {d} t}}}$

Следовательно, кривую релаксации можно использовать для определения скорости вязкопластической деформации и, следовательно, вязкости демпфера в одномерной модели вязкопластичного материала. Остаточное значение, которое достигается, когда напряжение выходит на плато в конце теста релаксации, соответствует верхнему пределу упругости. Для некоторых материалов, таких как каменная соль, такой верхний предел упругости достигается при очень малом значении напряжения, и испытания на релаксацию могут продолжаться более года без какого-либо наблюдаемого плато в напряжении.

Важно отметить, что тесты на релаксацию чрезвычайно трудно выполнять, потому что поддержание состояния ${ Displaystyle { cfrac { mathrm {d} { boldsymbol { varepsilon}}} { mathrm {d} t}} = 0}$ в тесте требует значительной деликатности.^[20]

Реологические модели вязкопластичности

Одномерные составляющие модели вязкопластичности, основанные на элементах пружинной решетки-ползунка, включают:^[3]идеально вязкопластическое твердое тело, эластичное идеально вязкопластическое твердое тело и упруговязкопластическое твердое тело отверждения. Элементы могут быть соединены в серии или в параллельно. В моделях, где элементы соединены последовательно, деформация является аддитивной, в то время как напряжение одинаково в каждом элементе. В параллельных соединениях напряжение является аддитивным, в то время как деформации одинаковы в каждом элементе. Многие из этих одномерных моделей можно обобщить до трех измерений для режима малых деформаций. В последующем обсуждении скорости деформации и напряжения со временем записываются как ${ displaystyle { dot { boldsymbol { varepsilon}}}}$ и ${ Displaystyle { точка { boldsymbol { sigma}}}}$, соответственно.

Совершенно вязкопластическое твердое тело (модель Нортона-Хоффа)

Рис. 5. Модель Нортона-Хоффа для идеально вязкопластичного твердого тела.

В идеально вязкопластическом твердом теле, также называемом моделью вязкопластичности Нортона-Хоффа, напряжение (как и для вязких жидкостей) является функцией скорости остаточной деформации. В модели не учитывается эффект упругости, т.е. ${ displaystyle { boldsymbol { varepsilon}} _ {e} = 0}$ и, следовательно, нет начального предела текучести, т.е. ${ displaystyle sigma _ {y} = 0}$. У вязкого дашпота есть ответ, который дает

${ displaystyle { boldsymbol { sigma}} = eta ~ { dot { boldsymbol { varepsilon}}} _ { mathrm {vp}} подразумевает { dot { boldsymbol { varepsilon}}} _ { mathrm {vp}} = { cfrac { boldsymbol { sigma}} { eta}}}$

куда ${ displaystyle eta}$ вязкость дашпота. В модели Нортона-Хоффа вязкость ${ displaystyle eta}$ является нелинейной функцией приложенного напряжения и определяется выражением

${ displaystyle eta = lambda left [{ cfrac { lambda} {|| { boldsymbol { sigma}} ||}} right] ^ {N-1}}$

куда ${ displaystyle N}$ - подгоночный параметр, λ - кинематическая вязкость материала и ${ displaystyle || { boldsymbol { sigma}} || = { sqrt {{ boldsymbol { sigma}}: { boldsymbol { sigma}}}} = { sqrt { sigma _ {ij} sigma _ {ij}}}}$. Тогда скорость вязкопластической деформации определяется соотношением

${ displaystyle { dot { boldsymbol { varepsilon}}} _ { mathrm {vp}} = { cfrac { boldsymbol { sigma}} { lambda}} left [{ cfrac {|| { boldsymbol { sigma}} ||} { lambda}} right] ^ {N-1}}$

В одномерном виде модель Нортона-Хоффа может быть выражена как

${ displaystyle sigma = lambda ~ left ({ dot { varepsilon}} _ { mathrm {vp}} right) ^ {1 / N}}$

Когда ${ displaystyle N = 1.0}$ твердое тело вязкоупругий.

Если предположить, что пластическое течение изохорный (сохранение объема), то указанное выше соотношение можно выразить в более привычной форме^[21]

${ displaystyle { boldsymbol {s}} = 2K ~ left ({ sqrt {3}} { dot { varepsilon}} _ { mathrm {eq}} right) ^ {m-1} ~ { dot { boldsymbol { varepsilon}}} _ { mathrm {vp}}}$

куда ${ displaystyle { boldsymbol {s}}}$ это девиаторное напряжение тензор, ${ displaystyle { dot { varepsilon}} _ { mathrm {eq}}}$ это эквивалентная деформация фон Мизеса скорость и ${ displaystyle K, м}$ параметры материала. Эквивалентная скорость деформации определяется как

${ displaystyle { dot { bar { epsilon}}} = { sqrt {{ frac {2} {3}} { dot { bar { bar { epsilon}}}}}: { dot { bar { bar { epsilon}}}}}}}$

Эти модели могут применяться в металлах и сплавах при температурах выше двух третей.^[21] их абсолютной температуры плавления (в градусах Кельвина) и полимеров / асфальта при повышенной температуре. Результаты испытаний такого материала на деформационное упрочнение, ползучесть и релаксацию показаны на рисунке 6.

Рис. 6: Реакция идеально вязкопластичного твердого тела на испытания на твердение, ползучесть и релаксацию.

Упругое идеально вязкопластическое твердое тело (модель Бингема – Нортона)

Рисунок 7. Эластичный идеально вязкопластический материал.

Два типа элементарных подходов могут быть использованы для создания упруго-идеально вязкопластической моды. В первом случае фрикционный элемент скольжения и демпфер располагаются параллельно, а затем последовательно соединяются с упругой пружиной, как показано на рисунке 7. Эта модель называется Модель Бингема – Максвелла (по аналогии с Модель Максвелла и Модель Бингема ) или Модель Бингема – Нортона.^[22] Во втором случае все три элемента расположены параллельно. Такая модель называется Модель Бингема – Кельвина по аналогии с Модель Кельвина.

Для упруго-идеально вязкопластических материалов упругая деформация больше не считается незначительной, но скорость пластической деформации зависит только от начального напряжения текучести и не влияет на упрочнение. Скользящий элемент представляет собой постоянное напряжение текучести при превышении предела упругости независимо от деформации. Модель может быть выражена как

${ displaystyle { begin {align} & { boldsymbol { sigma}} = { mathsf {E}} ~ { boldsymbol { varepsilon}} && mathrm {for} ~ | { boldsymbol { sigma }} | < sigma _ {y} & { dot { boldsymbol { varepsilon}}} = { dot { boldsymbol { varepsilon}}} _ { mathrm {e}} + { точка { boldsymbol { varepsilon}}} _ { mathrm {vp}} = { mathsf {E}} ^ {- 1} ~ { dot { boldsymbol { sigma}}} + { cfrac { boldsymbol { sigma}} { eta}} left [1 - { cfrac { sigma _ {y}} { | { boldsymbol { sigma}} |}} right] && mathrm {для } ~ | { boldsymbol { sigma}} | geq sigma _ {y} end {выравнивается}}}$

куда ${ displaystyle eta}$ - вязкость элемента дашпота. Если элемент dashpot имеет ответ в форме Norton

${ displaystyle { cfrac { boldsymbol { sigma}} { eta}} = { cfrac { boldsymbol { sigma}} { lambda}} left [{ cfrac { | | { boldsymbol { сигма}} |} { lambda}} right] ^ {N-1}}$

мы получаем модель Бингема – Нортона

${ displaystyle { dot { boldsymbol { varepsilon}}} = { mathsf {E}} ^ {- 1} ~ { dot { boldsymbol { sigma}}} + { cfrac { boldsymbol { sigma}} { lambda}} left [{ cfrac { | { boldsymbol { sigma}} |} { lambda}} right] ^ {N-1} left [1 - { cfrac { sigma _ {y}} { | { boldsymbol { sigma}} |}} right] quad mathrm {for} ~ | { boldsymbol { sigma}} | geq sigma _ {y}}$

Другие выражения для скорости деформации также можно найти в литературе.^[22] в общем виде

${ displaystyle { dot { boldsymbol { varepsilon}}} = { mathsf {E}} ^ {- 1} ~ { dot { boldsymbol { sigma}}} + f ({ boldsymbol { sigma }}, sigma _ {y}) ~ { boldsymbol { sigma}} quad mathrm {for} ~ | { boldsymbol { sigma}} | geq sigma _ {y}}$

Результаты испытаний такого материала на деформационное упрочнение, ползучесть и релаксацию показаны на рисунке 8.

Рис. 8. Реакция упругого идеально вязкопластического твердого тела на испытания на упрочнение, ползучесть и релаксацию.

Упруговязкопластическое твердое тело

Упруго-вязкопластический материал с деформационное упрочнение описывается уравнениями, аналогичными уравнениям для упруговязкопластического материала с идеальной пластичностью. Однако в этом случае напряжение зависит как от скорости пластической деформации, так и от самой пластической деформации. Для упруговязкопластического материала напряжение после превышения предела текучести продолжает увеличиваться за пределы начальной точки текучести. Это означает, что предел текучести в элементе скольжения увеличивается с деформацией, и модель может быть выражена в общих терминах как

${ displaystyle { begin {align} & { boldsymbol { varepsilon}} = { boldsymbol { varepsilon}} _ { mathrm {e}} = { mathsf {E}} ^ {- 1} ~ { boldsymbol { sigma}} = ~ { boldsymbol { varepsilon}} && mathrm {for} ~ || { boldsymbol { sigma}} || < sigma _ {y} & { dot { boldsymbol { varepsilon}}} = { dot { boldsymbol { varepsilon}}} _ { mathrm {e}} + { dot { boldsymbol { varepsilon}}} _ { mathrm {vp}} = { mathsf {E}} ^ {- 1} ~ { dot { boldsymbol { sigma}}} + f ({ boldsymbol { sigma}}, sigma _ {y}, { boldsymbol { varepsilon}} _ { mathrm {vp}}) ~ { boldsymbol { sigma}} && mathrm {for} ~ || { boldsymbol { sigma}} || geq sigma _ {y} end {выровнено}}}$.

Эта модель применяется, когда металлы и сплавы находятся при средних и высоких температурах, а древесина - при высоких нагрузках. Результаты испытаний такого материала на деформационное упрочнение, ползучесть и релаксацию показаны на рисунке 9.

Рисунок 9. Реакция упруговязкопластического твердого тела на испытания на упрочнение, ползучесть и релаксацию.

Модели пластичности, зависящие от скорости деформации

Классические феноменологические модели вязкопластичности для небольшие штаммы обычно делятся на два типа:^[3]

• формулировка Perzyna
• формулировка Дуво-Лайонса

Состав Perzyna

В формулировке Perzyna предполагается, что скорость пластической деформации задается определяющим соотношением вида

${ displaystyle { dot { varepsilon}} _ { mathrm {vp}} = { cfrac { left langle f ({ boldsymbol { sigma}}, { boldsymbol {q}}) right rangle} { tau}} { cfrac { partial f} { partial { boldsymbol { sigma}}}} = { begin {cases} { cfrac {f ({ boldsymbol { sigma}}, { boldsymbol {q}})} { tau}} { cfrac { partial f} { partial { boldsymbol { sigma}}}}} & { rm {if}} ~ f ({ boldsymbol { sigma}}, { boldsymbol {q}})> 0 0 & { rm {иначе}} end {case}}}$

куда ${ displaystyle f (.,.)}$ это функция доходности, ${ displaystyle { boldsymbol { sigma}}}$ это Напряжение Коши, ${ displaystyle { boldsymbol {q}}}$ представляет собой набор внутренних переменных (таких как пластическая деформация ${ displaystyle { boldsymbol { varepsilon}} _ { mathrm {vp}}}$), ${ Displaystyle тау}$ время релаксации. Обозначение ${ displaystyle langle dots rangle}$ обозначает Брекеты Маколея. Правило потока, используемое в различных версиях Чабоче модель является частным случаем правила потока Пержины^[23] и имеет вид

${ displaystyle { dot { varepsilon}} _ { mathrm {vp}} = left langle { frac {f} {f_ {0}}} right rangle ^ {n} ({ boldsymbol { sigma}} - { boldsymbol { chi}})}$

куда ${ displaystyle f_ {0}}$ квазистатическое значение ${ displaystyle f}$ и ${ displaystyle { boldsymbol { chi}}}$ это обратное напряжение. Несколько моделей для бэкстресса также известны под названием Модель Чабош.

Формулировка Дуво-Лайонса

Формулировка Duvaut-Lions эквивалентна формулировке Perzyna и может быть выражена как

${ displaystyle { dot { varepsilon}} _ { mathrm {vp}} = { begin {case} { mathsf {C}} ^ {- 1}: { cfrac {{ boldsymbol { sigma} } - { mathcal {P}} { boldsymbol { sigma}}} { tau}} & { rm {{if} ~ f ({ boldsymbol { sigma}}, { boldsymbol {q}}) )> 0}} 0 & { rm {иначе}} end {case}}}$

куда ${ displaystyle { mathsf {C}}}$ - тензор упругой жесткости, ${ Displaystyle { mathcal {P}} { boldsymbol { sigma}}}$ - ближайшая точечная проекция напряженного состояния на границу области, ограничивающей все возможные упругие напряженные состояния. Количество ${ Displaystyle { mathcal {P}} { boldsymbol { sigma}}}$ обычно находится из независимого от скорости решения проблемы пластичности.

Модели напряжения течения

Количество ${ displaystyle f ({ boldsymbol { sigma}}, { boldsymbol {q}})}$ представляет собой эволюцию поверхность текучести. Функция доходности ${ displaystyle f}$ часто выражается в виде уравнения, состоящего из некоторого инварианта напряжения и модели для предела текучести (или напряжения пластического течения). Примером является фон Мизес или же ${ displaystyle J_ {2}}$ пластичность. В этих ситуациях скорость пластической деформации рассчитывается так же, как и пластичность, не зависящая от скорости. В других ситуациях модель предела текучести позволяет напрямую вычислить скорость пластической деформации.

Для расчета пластичности используются многочисленные эмпирические и полуэмпирические модели напряжения течения. Следующие модели, зависящие от температуры и скорости деформации, представляют собой выборку моделей, используемых в настоящее время:

1. модель Джонсона – Кука
2. модель Стейнберга – Кохрана – Гинан – Лунда.
3. модель Зерилли – Армстронга.
4. Модель механического порогового напряжения.
5. модель Престона – Тонкс – Уоллеса.

Модель Джонсона – Кука (JC) ^[24] является чисто эмпирическим и является наиболее широко используемым из пяти. Однако эта модель демонстрирует нереально малую зависимость скорости деформации при высоких температурах. Модель Стейнберга – Кокрана – Гинан – Лунда (SCGL). ^[25][26] полуэмпирический. Модель является чисто эмпирической и не зависит от скорости деформации при высоких скоростях деформации. Расширение на основе вывиха на основе ^[27] используется при низких скоростях деформации. Модель SCGL широко используется сообществом физиков ударов. Модель Зерилли – Армстронга (ZA) ^[28] это простая физически обоснованная модель, которая широко использовалась. Более сложной моделью, основанной на идеях динамики дислокаций, является модель механического порогового напряжения (MTS).^[29] Эта модель была использована для моделирования пластической деформации меди, тантала,^[30] сплавы стали,^[31][32] и алюминиевые сплавы.^[33] Однако модель MTS ограничена скоростями деформации менее 10⁷/ с. Модель Престона – Тонкса – Уоллеса (PTW) ^[34] также имеет физическую основу и имеет форму, аналогичную модели MTS. Однако в модели PTW есть компоненты, которые могут моделировать пластическую деформацию в режиме перегруженного скачка (скорости деформации выше 10⁷/ с). Следовательно, эта модель действительна для самого большого диапазона скоростей деформации среди пяти моделей напряжения течения.

Модель напряжения течения Джонсона – Кука

Модель Джонсона – Кука (JC) ^[24] является чисто эмпирическим и дает следующее соотношение для напряжения течения (${ displaystyle sigma _ {y}}$)

${ displaystyle { text {(1)}} qquad sigma _ {y} ( varepsilon _ { rm {p}}, { dot { varepsilon _ { rm {p}}}}, т ) = left [A + B ( varepsilon _ { rm {p}}) ^ {n} right] left [1 + C ln ({ dot { varepsilon _ { rm {p}}) }} ^ {*}) right] left [1- (T ^ {*}) ^ {m} right]}$

куда ${ displaystyle varepsilon _ { rm {p}}}$ это эквивалентная пластическая деформация, ${ displaystyle { dot { varepsilon _ { rm {p}}}}}$ пластик скорость деформации, и ${ displaystyle A, B, C, n, m}$ материальные константы.

Нормализованная скорость деформации и температура в уравнении (1) определяются как

${ displaystyle { dot { varepsilon _ { rm {p}}}} ^ {*}: = { cfrac { dot { varepsilon _ { rm {p}}}} { dot { varepsilon _ { rm {p0}}}} qquad { text {and}} qquad T ^ {*}: = { cfrac {(T-T_ {0})} {(T_ {m} -T_ {0})}}}$

куда ${ displaystyle { dot { varepsilon _ { rm {p0}}}}}$ - эффективная скорость пластической деформации квазистатического испытания, используемого для определения параметров текучести и упрочнения A, B и n. Это не так, как часто думают, просто параметр, позволяющий ${ Displaystyle { точка { varepsilon _ { rm {p}}}} ^ {*}}$ безразмерный.^[35] ${ displaystyle T_ {0}}$ - эталонная температура, и ${ displaystyle T_ {m}}$ это ссылка температура плавления. Для условий, когда ${ displaystyle T ^ {*} <0}$, мы предполагаем, что ${ displaystyle m = 1}$.

Модель напряжения течения Стейнберга – Кохрана – Гинан – Лунда

Модель Steinberg – Cochran – Guinan – Lund (SCGL) - это полуэмпирическая модель, разработанная Steinberg et al.^[25] для ситуаций с высокой скоростью деформации и распространены на материалы с низкой скоростью деформации и ОЦК материалы Стейнбергом и Лундом.^[26] Напряжение течения в этой модели определяется выражением

${ displaystyle { text {(2)}} qquad sigma _ {y} ( varepsilon _ { rm {p}}, { dot { varepsilon _ { rm {p}}}}, т ) = left [ sigma _ {a} f ( varepsilon _ { rm {p}}) + sigma _ {t} ({ dot { varepsilon _ { rm {p}}}}, T ) right] { frac { mu (p, T)} { mu _ {0}}}; quad sigma _ {a} f leq sigma _ { text {max}} ~~ { текст {и}} ~~ sigma _ {t} leq sigma _ {p}}$

куда ${ Displaystyle sigma _ {а}}$ - атермическая составляющая напряжения течения, ${ Displaystyle F ( varepsilon _ { rm {p}})}$ - функция деформационного упрочнения, ${ displaystyle sigma _ {t}}$ - термически активированная составляющая напряжения течения, ${ Displaystyle му (п, Т)}$ - модуль сдвига, зависящий от давления и температуры, а ${ displaystyle mu _ {0}}$ - модуль сдвига при стандартной температуре и давлении. Величина насыщения атермического напряжения составляет ${ displaystyle sigma _ { text {max}}}$. Насыщение термически активированного напряжения - это Стресс Пайерлса (${ displaystyle sigma _ {p}}$). Модуль сдвига для этой модели обычно вычисляется с помощью Модель модуля сдвига Штейнберга – Кохрана – Гинана..

Функция деформационного упрочнения (${ displaystyle f}$) имеет вид

${ displaystyle f ( varepsilon _ { rm {p}}) = [1+ beta ( varepsilon _ { rm {p}} + varepsilon _ { rm {p}} i)] ^ {n }}$

куда ${ displaystyle beta, n}$ - параметры деформационного упрочнения, а ${ Displaystyle varepsilon _ { rm {p}} я}$ - начальная эквивалентная пластическая деформация.

Тепловая составляющая (${ displaystyle sigma _ {t}}$) вычисляется с использованием алгоритма деления пополам из следующего уравнения.^[26][27]

${ displaystyle { dot { varepsilon _ { rm {p}}}} = left [{ frac {1} {C_ {1}}} exp left [{ frac {2U_ {k}}] {k_ {b} ~ T}} left (1 - { frac { sigma _ {t}} { sigma _ {p}}} right) ^ {2} right] + { frac {C_ {2}} { sigma _ {t}}} right] ^ {- 1}; quad sigma _ {t} leq sigma _ {p}}$

куда ${ displaystyle 2U_ {k}}$ это энергия для образования изгиб-пара в сегмент вывиха длины ${ displaystyle L_ {d}}$, ${ displaystyle k_ {b}}$ это Постоянная Больцмана, ${ displaystyle sigma _ {p}}$ это Стресс Пайерлса. Константы ${ displaystyle C_ {1}, C_ {2}}$ задаются соотношениями

${ displaystyle C_ {1}: = { frac { rho _ {d} L_ {d} ab ^ {2} nu} {2w ^ {2}}}; quad C_ {2}: = { гидроразрыв {D} { rho _ {d} b ^ {2}}}}$

куда ${ displaystyle rho _ {d}}$ это плотность дислокаций, ${ displaystyle L_ {d}}$ - длина дислокационного сегмента, ${ displaystyle a}$ это расстояние между Долины пайерлса, ${ displaystyle b}$ это величина Вектор гамбургеров, ${ displaystyle nu}$ это Частота Дебая, ${ displaystyle w}$ это ширина петля петли, и ${ displaystyle D}$ это коэффициент трения.

Модель напряжения течения Зерилли – Армстронга

Модель Зерилли – Армстронга (ZA) ^[28][36][37] основан на упрощенной механике дислокаций. Общий вид уравнения для напряжения течения:

${ displaystyle { text {(3)}} qquad sigma _ {y} ( varepsilon _ { rm {p}}, { dot { varepsilon _ { rm {p}}}}, т ) = sigma _ {a} + B exp (- beta T) + B_ {0} { sqrt { varepsilon _ { rm {p}}}} exp (- alpha T) ~.}$

В этой модели ${ Displaystyle sigma _ {а}}$ - атермическая составляющая напряжения течения, определяемая по формуле

${ displaystyle sigma _ {a}: = sigma _ {g} + { frac {k_ {h}} { sqrt {l}}} + K varepsilon _ { rm {p}} ^ {n },}$

куда ${ displaystyle sigma _ {g}}$ - вклад растворенных веществ и начальной плотности дислокаций, ${ displaystyle k_ {h}}$ - интенсивность микроструктурных напряжений, ${ displaystyle l}$ - средний диаметр зерна, ${ displaystyle K}$ равен нулю для материалов с ГЦК, ${ displaystyle B, B_ {0}}$ материальные константы.

В термически активируемых условиях функциональные формы показателей степени ${ displaystyle alpha}$ и ${ displaystyle beta}$ находятся

${ displaystyle alpha = alpha _ {0} - alpha _ {1} ln ({ dot { varepsilon _ { rm {p}}}}); quad beta = beta _ {0 } - beta _ {1} ln ({ dot { varepsilon _ { rm {p}}}});}$

куда ${ displaystyle alpha _ {0}, alpha _ {1}, beta _ {0}, beta _ {1}}$ параметры материала, которые зависят от типа материала (ГЦК, ОЦК, ГПУ, сплавы). Модель Зерилли – Армстронга была модифицирована ^[38] для лучшей работы при высоких температурах.

Модель механического порогового напряжения, напряжения течения

Модель механического порогового напряжения (MTS) ^[29][39][40]) имеет вид

${ displaystyle { text {(4)}} qquad sigma _ {y} ( varepsilon _ { rm {p}}, { dot { varepsilon}}, T) = sigma _ {a} + (S_ {i} sigma _ {i} + S_ {e} sigma _ {e}) { frac { mu (p, T)} { mu _ {0}}}}$

куда ${ displaystyle sigma _ {a}}$ - атермическая составляющая механического порогового напряжения, ${ displaystyle sigma _ {я}}$ является составляющей напряжения течения из-за внутренних барьеров для термически активированного движения дислокаций и дислокационно-дислокационных взаимодействий, ${ displaystyle sigma _ {e}}$ - составляющая напряжения течения из-за эволюции микроструктуры с увеличением деформации (деформационное упрочнение), (${ displaystyle S_ {i}, S_ {e}}$) являются масштабными коэффициентами, зависящими от температуры и скорости деформации, и ${ displaystyle mu _ {0}}$ - модуль сдвига при 0 K и атмосферном давлении.

Коэффициенты масштабирования принимают Аррениус форма

${ displaystyle { begin {align} S_ {i} & = left [1- left ({ frac {k_ {b} ~ T} {g_ {0i} b ^ {3} mu (p, T )}} ln { frac { dot { varepsilon _ { rm {0}}}} { dot { varepsilon}}} right) ^ {1 / q_ {i}} right] ^ { 1 / p_ {i}} S_ {e} & = left [1- left ({ frac {k_ {b} ~ T} {g_ {0e} b ^ {3} mu (p, T )}} ln { frac { dot { varepsilon _ { rm {0}}}} { dot { varepsilon}}} right) ^ {1 / q_ {e}} right] ^ { 1 / р_ {е}} конец {выровнено}}}$

куда ${ displaystyle k_ {b}}$ - постоянная Больцмана, ${ displaystyle b}$ - величина вектора Бюргерса, (${ displaystyle g_ {0i}, g_ {0e}}$) - нормированные энергии активации, (${ displaystyle { dot { varepsilon}}, { dot { varepsilon _ { rm {0}}}}}$) - скорость деформации и эталонная скорость деформации, а (${ displaystyle q_ {i}, p_ {i}, q_ {e}, p_ {e}}$) являются константами.

Компонент деформационного упрочнения порогового механического напряжения (${ displaystyle sigma _ {e}}$) дается эмпирическим модифицированным Закон голоса

${ displaystyle { text {(5)}} qquad { frac {d sigma _ {e}} {d varepsilon _ { rm {p}}}} = theta ( sigma _ {e} )}$

куда

${ displaystyle { begin {align} theta ( sigma _ {e}) & = theta _ {0} [1-F ( sigma _ {e})] + theta _ {IV} F ( sigma _ {e}) theta _ {0} & = a_ {0} + a_ {1} ln { dot { varepsilon _ { rm {p}}}} + a_ {2} { sqrt { dot { varepsilon _ { rm {p}}}}} - a_ {3} T F ( sigma _ {e}) & = { cfrac { tanh left ( alpha { cfrac { sigma _ {e}} { sigma _ {es}}} right)} { tanh ( alpha)}} ln ({ cfrac { sigma _ {es}} { sigma _ {0es}}}) & = left ({ frac {kT} {g_ {0es} b ^ {3} mu (p, T)}} right) ln left ({ cfrac { точка { varepsilon _ { rm {p}}}} { dot { varepsilon _ { rm {p}}}}} right) end {align}}}$

и ${ displaystyle theta _ {0}}$ - упрочнение из-за скопления дислокаций, ${ displaystyle theta _ {IV}}$ - вклад от упрочнения IV стадии, (${ displaystyle a_ {0}, a_ {1}, a_ {2}, a_ {3}, alpha}$) - константы, ${ displaystyle sigma _ {es}}$ - напряжение при нулевой скорости деформационного упрочнения, ${ displaystyle sigma _ {0es}}$ - пороговое напряжение насыщения для деформации при 0 K, ${ displaystyle g_ {0es}}$ константа, а ${ displaystyle { dot { varepsilon _ { rm {p}}}}}$ - максимальная скорость деформации. Обратите внимание, что максимальная скорость деформации обычно ограничивается примерно ${ displaystyle 10 ^ {7}}$/ с.

Модель напряжения течения Престона – Тонкса – Уоллеса

Модель Престона – Тонкса – Уоллеса (PTW) ^[34] пытается предоставить модель напряжения течения для экстремальных скоростей деформации (до 10¹¹/ с) и температуры до плавления. В модели использован линейный закон упрочнения Воца. Напряжение потока PTW определяется выражением

${ displaystyle { text {(6)}} qquad sigma _ {y} ( varepsilon _ { rm {p}}, { dot { varepsilon _ { rm {p}}}}, т ) = { begin {case} 2 left [ tau _ {s} + alpha ln left [1- varphi exp left (- beta - { cfrac { theta varepsilon _ { rm {p}}} { alpha varphi}} right) right] right] mu (p, T) & { text {тепловой режим}} 2 tau _ {s} mu ( p, T) & { text {ударный режим}} end {cases}}}$

с

${ displaystyle alpha: = { frac {s_ {0} - tau _ {y}} {d}}; quad beta: = { frac { tau _ {s} - tau _ {y }} { alpha}}; quad varphi: = exp ( beta) -1}$

куда ${ Displaystyle тау _ {s}}$ - нормализованное напряжение насыщения деформационного упрочнения, ${ displaystyle s_ {0}}$ это ценность ${ Displaystyle тау _ {s}}$ при 0К, ${ displaystyle tau _ {y}}$ - нормированный предел текучести, ${ displaystyle theta}$ - постоянная упрочнения в законе упрочнения Воуса, а ${ displaystyle d}$ - безразмерный параметр материала, который изменяет закон упрочнения Воуса.

Напряжение насыщения и предел текучести определяются как

${ displaystyle { begin {align} tau _ {s} & = max left {s_ {0} - (s_ {0} -s _ { infty}) { rm {{erf} left [ kappa { hat {T}} ln left ({ cfrac { gamma { dot { xi}}} { dot { varepsilon _ { rm {p}}}}} right) right], s_ {0} left ({ cfrac { dot { varepsilon _ { rm {p}}}} { gamma { dot { xi}}}}} right) ^ {s_ {1 }}}} right } tau _ {y} & = max left {y_ {0} - (y_ {0} -y _ { infty}) { rm {{erf} left [ kappa { hat {T}} ln left ({ cfrac { gamma { dot { xi}}} { dot { varepsilon _ { rm {p}}}}} right) right], min left {y_ {1} left ({ cfrac { dot { varepsilon _ { rm {p}}}}} { gamma { dot { xi}}}} справа) ^ {y_ {2}}, s_ {0} left ({ cfrac { dot { varepsilon _ { rm {p}}}}} { gamma { dot { xi}}}} вправо) ^ {s_ {1}} right }}} right } end {align}}}$

куда ${ displaystyle s _ { infty}}$ это ценность ${ Displaystyle тау _ {s}}$ близкой к температуре плавления, (${ displaystyle y_ {0}, y _ { infty}}$) - значения ${ displaystyle tau _ {y}}$ при 0 К и близкой к плавлению соответственно ${ Displaystyle ( каппа, гамма)}$ материальные константы, ${ displaystyle { hat {T}} = T / T_ {m}}$, (${ displaystyle s_ {1}, y_ {1}, y_ {2}}$) - параметры материала для режима высокой скорости деформации, а

${ displaystyle { dot { xi}} = { frac {1} {2}} left ({ cfrac {4 pi rho} {3M}} right) ^ {1/3} left ({ cfrac { mu (p, T)} { rho}} right) ^ {1/2}}$

куда ${ displaystyle rho}$ это плотность, а ${ displaystyle M}$ - атомная масса.

Смотрите также

• Вязкоупругость
• Бингем пластик
• Dashpot
• Ползучесть (деформация)
• Пластичность (физика)
• Механика сплошной среды
• Квазитвердый

Рекомендации