Уравнение Аррениуса - Arrhenius equation

В физическая химия, то Уравнение Аррениуса представляет собой формулу температурной зависимости скорость реакции. Уравнение было предложено Сванте Аррениус в 1889 г. на основе работы голландского химика Якобус Хенрикус ван 'т Хофф который заметил в 1884 году, что уравнение Ван 'т Гоффа для температурной зависимости константы равновесия предлагает такую формулу для скоростей как прямой, так и обратной реакции. Это уравнение имеет широкое и важное применение при определении скорости химических реакций и для расчета энергии активации. Аррениус дал физическое обоснование и интерпретацию этой формулы.^[1]^[2]^[3] В настоящее время его лучше всего рассматривать как эмпирический отношения.^[4]^:188 Его можно использовать для моделирования температурных изменений коэффициентов диффузии, заполнения кристаллических вакансий, скорости ползучести и многих других термически индуцированных процессов / реакций. В Уравнение Эйринга, разработанный в 1935 году, также выражает взаимосвязь между скоростью и энергией.

Уравнение

Практически во всех практических случаях

{ displaystyle E_ {a} gg RT}

и k быстро увеличивается с Т.

Математически, при очень высоких температурах, так что

{ displaystyle E_ {a} ll RT}

, k выравнивается и приближается А как предел, но в практических условиях этого не происходит.

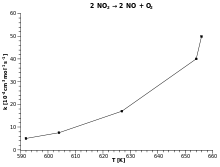
Уравнение Аррениуса дает зависимость константа скорости химической реакции на абсолютная температура так как

{ displaystyle k = Ae ^ { frac {-E _ { rm {a}}} {RT}},}

где

k

это константа скорости (частота столкновений, приводящих к реакции),

Т

это абсолютная температура (в кельвины ),

А

это предэкспоненциальный множитель, константа для каждой химической реакции,

E а

это энергия активации для реакции (в тех же единицах, что и RT),

р

это универсальная газовая постоянная.^[1]^[2]^[3]

В качестве альтернативы уравнение может быть выражено как

{ displaystyle k = Ae ^ { frac {-E _ { rm {a}}} {k _ { rm {B}} T}},}

где

E а

это энергия активации для реакции (в тех же единицах, что и k_BТ),

k B

это Постоянная Больцмана.

Единственная разница в единицах энергии $E а$ : первая форма использует энергию на моль, что является обычным в химии, в то время как последняя форма использует энергию на молекула напрямую, что является обычным в физике. Различные единицы учитываются при использовании либо газовая постоянная, $р$ , или Постоянная Больцмана, $k B$ , как множитель температуры $Т$ .

Единицы предэкспоненциального множителя $А$ идентичны таковым для константы скорости и будут варьироваться в зависимости от порядка реакции. Если реакция первого порядка, у нее есть единицы: s⁻¹, и по этой причине его часто называют частота фактор или частота попыток реакции. Проще говоря, $k$ это количество столкновений, которые приводят к реакции в секунду, $А$ это количество столкновений (ведущих к реакции или нет) в секунду, происходящих при правильной ориентации для реакции^[5] и ${ displaystyle e ^ {- E _ { rm {a}} / (RT)}}$ это вероятность того, что любое данное столкновение приведет к реакции. Видно, что либо повышение температуры, либо уменьшение энергии активации (например, за счет использования катализаторы ) приведет к увеличению скорости реакции.

Учитывая небольшой температурный диапазон кинетических исследований, разумно аппроксимировать энергию активации как не зависящую от температуры. Точно так же в широком диапазоне практических условий слабая температурная зависимость предэкспоненциального множителя пренебрежимо мала по сравнению с температурной зависимостью ${ Displaystyle ехр (-E _ { rm {a}} / (RT))}$ фактор; кроме случая "безбарьерного" распространение -ограниченные реакции, и в этом случае преэкспоненциальный фактор является доминирующим и непосредственно наблюдаемым.

Заговор Аррениуса

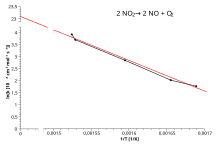
Линейный график Аррениуса: lnk против 1 /Т.

Принимая натуральный логарифм уравнения Аррениуса дает:

{ displaystyle ln k = ln A - { frac {E _ { rm {a}}} {R}} { frac {1} {T}}.}

Переставляем урожайность:

{ displaystyle ln k = { frac {-E _ { rm {a}}} {R}} left ({ frac {1} {T}} right) + ln A.}

Он имеет ту же форму, что и уравнение для прямой линии:

{ displaystyle y = mx + b,}

где Икс это взаимный из Т.

Итак, когда реакция имеет константу скорости, которая подчиняется уравнению Аррениуса, график lnk против Т⁻¹ дает прямую линию, градиент и точку пересечения которой можно использовать для определения E_а и А . Эта процедура стала настолько распространенной в экспериментальной химической кинетике, что практикующие врачи стали использовать ее для определить энергия активации реакции. То есть энергия активации определяется как (-р) умноженное на наклон участка lnk vs. (1 /Т):

{ Displaystyle E _ { rm {a}} Equiv -R left [{ frac { partial ln k} { partial (1 / T)}} right] _ {P}.}

Модифицированное уравнение Аррениуса

Модифицированное уравнение Аррениуса^[6] делает явной температурную зависимость предэкспоненциального множителя. Модифицированное уравнение обычно имеет вид

{ displaystyle k = AT ^ {n} e ^ {- E _ { rm {a}} / (RT)}.}

Исходное выражение Аррениуса выше соответствует п = 0. Установленные константы скорости обычно лежат в диапазоне −1 < п < 1. Теоретический анализ дает различные прогнозы для п. Было указано, что «на основе температурных исследований константы скорости невозможно установить, были ли предсказанные Т^1/2 зависимость предэкспоненциального множителя наблюдается экспериментально ».^[4]^:190 Однако, если доступны дополнительные доказательства из теории и / или эксперимента (например, зависимость от плотности), нет никаких препятствий для точной проверки закона Аррениуса.

Еще одна распространенная модификация - это растянутая экспонента форма^{[нужна цитата ]}

{ Displaystyle к = А ехр влево [- влево ({ гидроразрыва {E_ {а}} {RT}} вправо) ^ { бета} вправо],}

где β является безразмерным числом порядка 1. Это обычно рассматривается как чисто эмпирическая поправка или фактор выдумки чтобы модель соответствовала данным, но может иметь теоретическое значение, например, показывать наличие диапазона энергий активации или в особых случаях, таких как Mott скачкообразное изменение диапазона.

Теоретическая интерпретация уравнения

Концепция энергии активации Аррениуса

Аррениус утверждал, что для превращения реагентов в продукты они должны сначала получить минимальное количество энергии, называемое энергией активации. E_а. При абсолютной температуре Т, доля молекул, кинетическая энергия которых превышает E_а можно рассчитать из статистическая механика. Концепция чего-либо энергия активации объясняет экспоненциальный характер отношений, и так или иначе он присутствует во всех кинетических теориях.

В расчетах констант скорости реакции используется усреднение энергии по Распределение Максвелла – Больцмана с участием ${ displaystyle E _ { rm {a}}}$ как нижняя граница и поэтому часто бывают типа неполные гамма-функции, которые оказываются пропорциональными ${ displaystyle e ^ { frac {-E _ { rm {a}}} {RT}}}$ .

Теория столкновений

Один из подходов - это теория столкновений химических реакций, разработанных Макс Траутц и Уильям Льюис в 1916–18 гг. Согласно этой теории, молекулы должны реагировать, если они сталкиваются с относительной кинетической энергией вдоль линии их центров, которая превышает E_а. Число бинарных столкновений двух разнородных молекул в секунду на единицу объема составляет^[7]

{ displaystyle Z_ {AB} = n_ {A} n_ {B} d_ {AB} ^ {2} { sqrt { frac {8 pi k _ { rm {B}} T} { mu _ {AB }}}},}

где п_А и п_B являются числовая плотность молекул А и B, d_AB средний диаметр А и B, Т это температура, умноженная на Постоянная Больцмана k_B преобразовать в единицы энергии, и μ_AB это уменьшенная масса.

Константа скорости затем рассчитывается как ${ displaystyle k = Z_ {AB} e ^ { frac {-E _ { rm {a}}} {RT}},}$ так что теория столкновений предсказывает, что предэкспоненциальный множитель равен числу столкновений Z_AB. Однако для многих реакций это плохо согласуется с экспериментом, поэтому константа скорости записывается как ${ displaystyle k = PZ_ {AB} e ^ { frac {-E _ { rm {a}}} {RT}},}$ . Вот п эмпирический стерический фактор, часто намного меньше 1, что интерпретируется как доля достаточно энергичных столкновений, при которых две молекулы имеют правильную взаимную ориентацию для реакции.^[7]

Теория переходного состояния

В Уравнение Эйринга, другое выражение, похожее на Аррениуса, появляется в "теория переходного состояния "химических реакций, сформулированных Вигнер, Айринг, Поланьи и Эванс в 1930-е гг. Уравнение Эйринга можно записать:

{ displaystyle k = { frac {k _ { rm {B}} T} {h}} e ^ {- { frac { Delta G ^ { ddagger}} {RT}}} = { frac { k _ { rm {B}} T} {h}} e ^ { frac { Delta S ^ { ddagger}} {R}} e ^ {- { frac { Delta H ^ { ddagger}} {RT}}},}

где ${ displaystyle Delta G ^ { ddagger}}$ = the Энергия Гиббса активации, ${ displaystyle Delta S ^ { ddagger}}$ это энтропия активации, ${ displaystyle Delta H ^ { ddagger}}$ это энтальпия активации, ${ Displaystyle к _ { rm {B}}}$ является Постоянная Больцмана, и ${ displaystyle h}$ является Постоянная Планка.^[8]

На первый взгляд это выглядит как экспонента, умноженная на коэффициент, равный линейный по температуре. Однако свободная энергия сама по себе зависит от температуры. Свободная энергия активации ${ displaystyle Delta G ^ { ddagger} = Delta H ^ { ddagger} -T Delta S ^ { ddagger}}$ представляет собой разность члена энтальпии и члена энтропии, умноженного на абсолютную температуру. Предэкспоненциальный множитель зависит в первую очередь от энтропии активации. Общее выражение снова принимает форму экспоненты Аррениуса (энтальпии, а не энергии), умноженной на медленно меняющуюся функцию Т. Точная форма температурной зависимости зависит от реакции и может быть рассчитана по формулам из статистическая механика с участием функции раздела реагентов и активированного комплекса.

Ограничения идеи энергии активации Аррениуса

Энергия активации Аррениуса и константа скорости k определяются экспериментально и представляют собой макроскопические параметры реакции, которые не просто связаны с пороговыми энергиями и успехом отдельных столкновений на молекулярном уровне. Рассмотрим конкретное столкновение (элементарную реакцию) между молекулами A и B. Угол столкновения, относительная поступательная энергия, внутренняя (особенно колебательная) энергия - все это будет определять вероятность того, что столкновение приведет к образованию молекулы продукта AB. Макроскопические измерения E и k являются результатом множества индивидуальных столкновений с разными параметрами столкновения. Чтобы исследовать скорость реакции на молекулярном уровне, эксперименты проводятся в условиях, близких к столкновению, и этот предмет часто называют динамикой молекулярных реакций.^[9]

Другая ситуация, когда объяснение параметров уравнения Аррениуса не оправдывает себя, заключается в гетерогенный катализ, особенно для реакций, которые показывают Кинетика Ленгмюра-Хиншелвуда. Ясно, что молекулы на поверхности не «сталкиваются» напрямую, и простое молекулярное поперечное сечение здесь не применимо. Вместо этого предэкспоненциальный множитель отражает перемещение по поверхности к активному участку.^[10]

Есть отклонения от закона Аррениуса во время стеклование во всех классах стеклообразующих веществ.^[11] Закон Аррениуса предсказывает, что движение структурных единиц (атомов, молекул, ионов и т.д.) должно замедляться в процессе стеклования с меньшей скоростью, чем наблюдается экспериментально. Другими словами, структурные единицы замедляются быстрее, чем это предсказывается законом Аррениуса. Это наблюдение является разумным, если предположить, что блоки должны преодолевать энергетический барьер с помощью энергии тепловой активации. Тепловая энергия должна быть достаточно высокой, чтобы обеспечить поступательное движение единиц, которое приводит к вязкое течение материала.

Смотрите также

Ускоренное старение
Уравнение Эйринга
Q10 (температурный коэффициент)
Уравнение Ван 'т Гоффа
Соотношение Клаузиуса – Клапейрона
Уравнение Гиббса – Гельмгольца.
Фронт сакуры - предсказано с использованием уравнения Аррениуса

использованная литература

^ ^а ^б Аррениус, С. А. (1889). "Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte". Z. Phys. Chem. 4: 96–116. Дои:10.1515 / зпч-1889-0408. S2CID 202553486.
^ ^а ^б Аррениус, С. А. (1889). "Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren". Z. Phys. Chem. 4: 226–48. Дои:10.1515 / зпч-1889-0116.
^ ^а ^б Лайдлер, К. Дж. (1987) Химическая кинетика, Третье издание, Harper & Row, стр. 42
^ ^а ^б Кеннет Коннорс, Химическая кинетика, 1990, издательство VCH Publishers Химическая кинетика: изучение скорости реакции в растворе в Google Книги
^ Зильберберг, Мартин С. (2006). Химия (четвертое изд.). Нью-Йорк: Макгроу-Хилл. п.696. ISBN 0-07-111658-3.
^ IUPAC Goldbook определение модифицированного уравнения Аррениуса.
^ ^а ^б Laidler, Keith J .; Мейзер, Джон Х. (1982). Физическая химия (1-е изд.). Бенджамин / Каммингс. С. 376–78. ISBN 0-8053-5682-7.
^ Laidler, Keith J .; Мейзер, Джон Х. (1982). Физическая химия (1-е изд.). Бенджамин / Каммингс. С. 378–83. ISBN 0-8053-5682-7.
^ Левин, Р. (2005) Динамика молекулярных реакций, Издательство Кембриджского университета
^ Слот, Thierry K .; Райли, Натан; Шиджу, Н. Равендран; Медлин, Дж. Уилл; Ротенберг, Гади (2020). «Экспериментальный подход для управления эффектами удержания на границах раздела катализатора». Химическая наука. 11 (40): 11024–11029. Дои:10.1039 / D0SC04118A. ISSN 2041-6520.
^ Bauer, Th .; Lunkenheimer, P .; Лоидл, А. (2013). «Кооперативность и замораживание молекулярного движения при стекловании». Письма с физическими проверками. 111 (22): 225702. arXiv:1306.4630. Bibcode:2013ПхРвЛ.111в5702Б. Дои:10.1103 / PhysRevLett.111.225702. PMID 24329455. S2CID 13720989.

Список используемой литературы

Полинг, Л. К. (1988). Общая химия. Dover Publications.
Лайдлер, К. Дж. (1987). Химическая кинетика (3-е изд.). Харпер и Роу.
Лайдлер, К. Дж. (1993). Мир физической химии. Издательство Оксфордского университета.

внешние ссылки

Растворимость диоксида углерода в полиэтилене - Использование уравнения Аррениуса для расчета растворимости частиц в полимерах

[Arrhenius96-1] а ^б Аррениус, С. А. (1889). "Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte". Z. Phys. Chem. 4: 96–116. Дои:10.1515 / зпч-1889-0408. S2CID 202553486.

[Arrhenius226-2] а ^б Аррениус, С. А. (1889). "Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren". Z. Phys. Chem. 4: 226–48. Дои:10.1515 / зпч-1889-0116.

[Laidler42-3] а ^б Лайдлер, К. Дж. (1987) Химическая кинетика, Третье издание, Harper & Row, стр. 42

[Connors-4] а ^б Кеннет Коннорс, Химическая кинетика, 1990, издательство VCH Publishers Химическая кинетика: изучение скорости реакции в растворе в Google Книги

[5] Зильберберг, Мартин С. (2006). Химия (четвертое изд.). Нью-Йорк: Макгроу-Хилл. п.696. ISBN 0-07-111658-3.

[6] IUPAC Goldbook определение модифицированного уравнения Аррениуса.

[LM-7] а ^б Laidler, Keith J .; Мейзер, Джон Х. (1982). Физическая химия (1-е изд.). Бенджамин / Каммингс. С. 376–78. ISBN 0-8053-5682-7.

[8] Laidler, Keith J .; Мейзер, Джон Х. (1982). Физическая химия (1-е изд.). Бенджамин / Каммингс. С. 378–83. ISBN 0-8053-5682-7.

[9] Левин, Р. (2005) Динамика молекулярных реакций, Издательство Кембриджского университета

[10] Слот, Thierry K .; Райли, Натан; Шиджу, Н. Равендран; Медлин, Дж. Уилл; Ротенберг, Гади (2020). «Экспериментальный подход для управления эффектами удержания на границах раздела катализатора». Химическая наука. 11 (40): 11024–11029. Дои:10.1039 / D0SC04118A. ISSN 2041-6520.

[11] Bauer, Th .; Lunkenheimer, P .; Лоидл, А. (2013). «Кооперативность и замораживание молекулярного движения при стекловании». Письма с физическими проверками. 111 (22): 225702. arXiv:1306.4630. Bibcode:2013ПхРвЛ.111в5702Б. Дои:10.1103 / PhysRevLett.111.225702. PMID 24329455. S2CID 13720989.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]