Модуль сдвига - Shear modulus
| Модуль сдвига | |
|---|---|
Общие символы | г, S |
| Единица СИ | паскаль |
Производные от другие количества | г = τ / γ г = E / 2(1+п ) |

В материаловедение, модуль сдвига или модуль жесткости, обозначаемый г, а иногда S или μ, определяется как отношение напряжение сдвига к деформация сдвига:[1]
где
- = напряжение сдвига
- это сила, которая действует
- это область, на которую действует сила
- = деформация сдвига. В машиностроении , в другом месте
- поперечное смещение
- начальная длина
Производные SI единицей модуля сдвига является паскаль (Па), хотя обычно выражается в гигапаскали (ГПа) или в тысячах фунтов на квадратный дюйм (тыс. фунтов / кв. дюйм). это размерная форма это M1L−1Т−2, заменяя сила от масса раз ускорение.
Объяснение
| Материал | Типичные значения для модуль сдвига (ГПа) (при комнатной температуре) |
|---|---|
| Алмаз[2] | 478.0 |
| Сталь[3] | 79.3 |
| Утюг[4] | 52.5 |
| Медь[5] | 44.7 |
| Титан[3] | 41.4 |
| Стекло[3] | 26.2 |
| Алюминий[3] | 25.5 |
| Полиэтилен[3] | 0.117 |
| Резина[6] | 0.0006 |
| Гранит[7][8] | 24 |
| Сланец[7][8] | 1.6 |
| Известняк[7][8] | 24 |
| Мел[7][8] | 3.2 |
| Песчаник[7][8] | 0.4 |
| Дерево | 4 |
Модуль сдвига - это одна из нескольких величин для измерения жесткости материалов. Все они возникают в обобщенном Закон Гука:
- Модуль для младших E описывает деформационную реакцию материала на одноосное напряжение в направлении этого напряжения (например, натягивание концов проволоки или размещение груза на вершине колонны, при этом проволока становится длиннее, а колонна теряет высоту),
- то Коэффициент Пуассона ν описывает реакцию в направлениях, ортогональных к этому одноосному напряжению (проволока становится тоньше, а столбик толще),
- то объемный модуль K описывает реакцию материала на (униформу) гидростатическое давление (как давление на дне океана или глубокого бассейна),
- то модуль сдвига г описывает реакцию материала на напряжение сдвига (например, резку тупыми ножницами). Эти модули не являются независимыми, и для изотропный материалы они связаны уравнениями .[9]
Модуль сдвига связан с деформацией твердого тела, когда оно испытывает силу, параллельную одной из его поверхностей, в то время как его противоположная поверхность испытывает противодействующую силу (например, трение). Если объект имеет форму прямоугольной призмы, он деформируется в параллелепипед. Анизотропный материалы, такие как дерево, бумага а также практически все монокристаллы демонстрируют различную реакцию материала на напряжение или деформацию при испытании в разных направлениях. В этом случае может потребоваться полная тензорное выражение упругих постоянных, а не одно скалярное значение.
Одно возможное определение жидкость будет материалом с нулевым модулем сдвига.
Поперечные волны
В однородных и изотропный твердые тела, есть два вида волн, волны давления и поперечные волны. Скорость поперечной волны, контролируется модулем сдвига,
где
- G - модуль сдвига
- это твердое тело плотность.
Модуль сдвига металлов
Модуль сдвига металлов обычно уменьшается с повышением температуры. При высоких давлениях модуль сдвига также увеличивается с приложенным давлением. Корреляция между температурой плавления, энергией образования вакансий и модулем сдвига наблюдалась во многих металлах.[13]
Существует несколько моделей, которые пытаются предсказать модуль сдвига металлов (и, возможно, сплавов). Модели модуля сдвига, которые использовались в расчетах пластического течения, включают:
- модель модуля сдвига MTS, разработанная[14] и используется в сочетании с моделью напряжения пластического течения «Механическое пороговое напряжение» (MTS).[15][16]
- модель модуля сдвига Steinberg-Cochran-Guinan (SCG), разработанная[17] и используется в сочетании с моделью напряжения течения Стейнберга-Кохрана-Гинан-Лунда (SCGL).
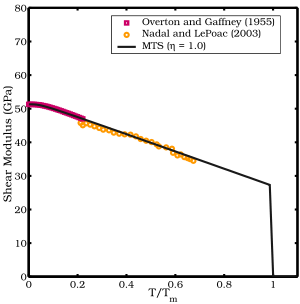
- модель модуля сдвига Надаля и Лепоака (NP)[12] который использует Теория Линдеманна для определения температурной зависимости и модели SCG для зависимости модуля сдвига от давления.
Модель МТС
Модель модуля сдвига MTS имеет вид:
где модуль сдвига при , и и материальные константы.
Модель SCG
Модель модуля сдвига Штейнберга-Кохрана-Гинана (SCG) зависит от давления и имеет вид
где, μ0 - модуль сдвига в исходном состоянии (Т = 300 К, п = 0, η = 1), п давление, а Т это температура.
Модель NP
Модель модуля сдвига Надаля-Ле Поака (NP) представляет собой модифицированную версию модели SCG. Эмпирическая температурная зависимость модуля сдвига в модели SCG заменена уравнением, основанным на Теория плавления Линдеманна. Модель модуля сдвига NP имеет вид:
где
и μ0 - модуль сдвига при абсолютном нуле и окружающем давлении, ζ - параметр материала, м это атомная масса, и ж это Постоянная Линдеманна.
Модуль релаксации сдвига
В модуль релаксации сдвига это зависящее от времени обобщение модуля сдвига[18] :
- .
Смотрите также
использованная литература
- ^ ИЮПАК, Сборник химической терминологии 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "модуль сдвига, г ". Дои:10.1351 / goldbook.S05635
- ^ McSkimin, HJ; Андреатч, П. (1972). «Модули упругости алмаза в зависимости от давления и температуры». J. Appl. Phys. 43 (7): 2944–2948. Bibcode:1972JAP .... 43.2944M. Дои:10.1063/1.1661636.
- ^ а б c d е Крэндалл, Даль, Ларднер (1959). Введение в механику твердого тела. Бостон: Макгроу-Хилл. ISBN 0-07-013441-3.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Рейн, Дж. (1961). «Упругие постоянные железа от 4,2 до 300 ° К». Физический обзор. 122 (6): 1714–1716. Bibcode:1961ПхРв..122.1714Р. Дои:10.1103 / PhysRev.122.1714.
- ^ Свойства материала
- ^ Спанос, Пит (2003). «Влияние системы отверждения на низкотемпературный динамический модуль сдвига натурального каучука». Резиновый мир.
- ^ а б c d е Хук, Эверт и Джонатан Д. Брей. Проектирование скальных склонов. CRC Press, 1981.
- ^ а б c d е Паризо, Уильям Г. Анализ конструкции в механике горных пород. CRC Press, 2017.
- ^ [Ландау Л.Д., Лифшиц Е.М. Теория упругости, т. 7. Курс теоретической физики. (2-е изд.) Пергамон: Оксфорд 1970, стр. 13]
- ^ Расчет модуля сдвига стекол
- ^ Overton, W .; Гаффни, Джон (1955). «Температурное изменение упругих постоянных кубических элементов. I. Медь». Физический обзор. 98 (4): 969. Bibcode:1955ПхРв ... 98..969О. Дои:10.1103 / PhysRev.98.969.
- ^ а б Надаль, Мари-Элен; Ле Поак, Филипп (2003). «Непрерывная модель модуля сдвига как функции давления и температуры вплоть до точки плавления: анализ и ультразвуковая проверка». Журнал прикладной физики. 93 (5): 2472. Bibcode:2003JAP .... 93.2472N. Дои:10.1063/1.1539913.
- ^ Марч, Н. Х., (1996), Электронная корреляция в молекулах и конденсированных фазах., Спрингер, ISBN 0-306-44844-0 п. 363
- ^ Варшни, Ю. (1970). «Температурная зависимость упругих постоянных». Физический обзор B. 2 (10): 3952–3958. Bibcode:1970PhRvB ... 2.3952В. Дои:10.1103 / PhysRevB.2.3952.
- ^ Чен, Шух Ронг; Грей, Джордж Т. (1996). «Основное поведение тантала и тантал-вольфрамовых сплавов». Металлургические операции и операции с материалами A. 27 (10): 2994. Bibcode:1996MMTA ... 27.2994C. Дои:10.1007 / BF02663849.
- ^ Гото, Д. М .; Garrett, R.K .; Bingert, J. F .; Chen, S. R .; Грей, Г. Т. (2000). «Описание модели конструктивной прочности механического порогового напряжения для стали HY-100». Металлургические операции и операции с материалами A. 31 (8): 1985–1996. Дои:10.1007 / s11661-000-0226-8.
- ^ Guinan, M; Стейнберг, Д. (1974). «Производные по давлению и температуре модуля изотропного поликристаллического сдвига для 65 элементов». Журнал физики и химии твердого тела. 35 (11): 1501. Bibcode:1974JPCS ... 35.1501G. Дои:10.1016 / S0022-3697 (74) 80278-7.
- ^ Рубинштейн, Майкл, 1956, 20 декабря - (2003). Полимерная физика. Колби, Ральф Х. Оксфорд: Издательство Оксфордского университета. п. 284. ISBN 019852059X. OCLC 50339757.CS1 maint: несколько имен: список авторов (ссылка на сайт)
| Формулы преобразования | |||||||
|---|---|---|---|---|---|---|---|
| Однородные изотропные линейные упругие материалы обладают своими упругими свойствами, однозначно определяемыми любыми двумя модулями из них; таким образом, для любых двух любых других модулей упругости можно рассчитать по этим формулам. | |||||||
| Заметки | |||||||
Есть два верных решения. | |||||||
| Не может использоваться, когда | |||||||




















![{ displaystyle mu (p, T) = { frac {1} {{ mathcal {J}} left ({ hat {T}} right)}} left [ left ( mu _ { 0} + { frac { partial mu} { partial p}} { frac {p} { eta ^ { frac {1} {3}}}} right) left (1 - { hat {T}} right) + { frac { rho} {Cm}} ~ T right]; quad C: = { frac { left (6 pi ^ {2} right) ^ { frac {2} {3}}} {3}} е ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a44071b746c80d284fb8d0e0f1ac54b8b3e1d20)
![{ displaystyle { mathcal {J}} ({ hat {T}}): = 1+ exp left [- { frac {1 + 1 / zeta} {1+ zeta / left (1 - { hat {T}} right)}} right] quad { text {for}} quad { hat {T}}: = { frac {T} {T_ {m}}} в [0,1+ zeta],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eec18d148b46152e0ff5d23af16b0440142b789b)






























































































