Уравнение Хагена – Пуазейля - Hagen–Poiseuille equation

В неидеальном динамика жидкостей, то Уравнение Хагена – Пуазейля, также известный как Закон Хагена – Пуазейля, Закон Пуазейля или же Уравнение Пуазейля, это физический закон что дает падение давления в несжимаемый и Ньютоновский жидкость в ламинарный поток протекает по длинной цилиндрической трубе постоянного сечения. Может успешно применяться для воздушного потока в легкое альвеолы, или поток через трубочку для питья или через игла для подкожных инъекций. Он был экспериментально выведен независимо Жан Леонар Мари Пуазей в 1838 г.^[1] и Готхильф Генрих Людвиг Хаген,^[2] и опубликован Пуазейлем в 1840–41 и 1846 годах.^[1] Теоретическое обоснование закона Пуазейля было дано Джордж Стоукс в 1845 г.^[3]

Предположения уравнения таковы, что жидкость несжимаемый и Ньютоновский; то поток ламинарный через трубу постоянного круглого поперечного сечения, значительно превышающую ее диаметр; и нет ускорение жидкости в трубе. Для скоростей и диаметров трубы выше порогового значения фактический поток жидкости не ламинарный, а бурный, что приводит к большим перепадам давления, чем рассчитывается по уравнению Хагена – Пуазейля.

Уравнение Пуазейля описывает перепад давления из-за вязкость жидкости; В жидкости все еще могут возникать другие типы перепадов давления (см. Демонстрацию здесь).^[4] Например, давление, необходимое для движения вязкой жидкости против силы тяжести, будет содержать и то, и другое, что требуется в законе Пуазейля. плюс это по мере необходимости в Уравнение Бернулли, так что в любой точке потока давление будет больше нуля (иначе потока не будет).

Другой пример - когда кровь течет в более узкую сужение, его скорость будет больше, чем у большего диаметра (из-за непрерывность из объемный расход ), а его давление будет ниже, чем в большем диаметре^[4] (из-за уравнения Бернулли). Однако вязкость крови вызовет дополнительный перепад давления в направлении потока, пропорциональный пройденной длине^[4] (по закону Пуазейля). Оба эффекта способствуют действительный падение давления.

Уравнение

В стандартных обозначениях кинетики жидкости:^[5][6][7]

${ displaystyle Delta p = { frac {8 mu LQ} { pi R ^ {4}}} = { frac {8 pi mu LQ} {A ^ {2}}}}$

куда:

Δп разница давлений между двумя концами,

L длина трубы,

μ это динамическая вязкость,

Q это объемный расход,

р это труба радиус,

А это поперечное сечение трубы.

Уравнение не выполняется вблизи входа в трубу.^[8]:3

Уравнение не работает в пределе низкой вязкости, широкой и / или короткой трубы. Низкая вязкость или широкая труба могут привести к турбулентному потоку, что требует использования более сложных моделей, таких как Уравнение Дарси – Вайсбаха.. Отношение длины к радиусу трубы должно быть больше одной сорок восьмой части Число Рейнольдса чтобы закон Хагена – Пуазейля действовал.^[9] Если труба слишком короткая, уравнение Хагена – Пуазейля может привести к нефизически высоким расходам; поток ограничен Принцип Бернулли, при менее ограничительных условиях,

${ displaystyle Delta p = { frac {1} {2}} rho v _ { text {max}} ^ {2} = { frac {1} {2}} rho left ({ frac {Q _ { max} {}} { pi R ^ {2}}} right) ^ {2} , , , rightarrow , , , Q _ { max} {} = pi R ^ {2} { sqrt { frac {2 Delta p} { rho}}},}$

потому что невозможно иметь давление ниже нуля (абсолютное) (не путать с манометрическое давление ) в несжимаемом потоке.

Связь с уравнением Дарси – Вейсбаха.

Обычно поток Хагена – Пуазейля подразумевает не только соотношение для перепада давления, приведенное выше, но и полное решение для ламинарного профиля потока, который является параболическим. Однако результат для падения давления может быть распространен на турбулентный поток путем определения эффективной турбулентной вязкости в случае турбулентного потока, даже если профиль потока в турбулентном потоке, строго говоря, не является фактически параболическим. В обоих случаях, ламинарном или турбулентном, падение давления связано с напряжением на стенке, которое определяет так называемый коэффициент трения. Напряжение стенки феноменологически определяется Уравнение Дарси – Вайсбаха. в области гидравлика, учитывая соотношение для коэффициента трения через число Рейнольдса. В случае ламинарного течения для круглого поперечного сечения:

${ displaystyle Lambda = { frac {64} { mathrm {Re}}}, quad mathrm {Re} = { frac { rho vd} { mu}},}$

куда Re это Число Рейнольдса, ρ - плотность жидкости, а v - средняя скорость потока, которая составляет половину максимальной скорости потока в случае ламинарного потока. Более полезным оказывается определение числа Рейнольдса в терминах средней скорости потока, потому что эта величина остается хорошо определенной даже в случае турбулентного потока, тогда как максимальная скорость потока может не быть или, в любом случае, может быть трудно сделать вывод. . В таком виде закон приближается к Коэффициент трения Дарси, то коэффициент потерь энергии (напора), коэффициент потерь на трение или же Коэффициент Дарси (трение) Λ в ламинарном потоке при очень малых скоростях в цилиндрической трубе. Теоретический вывод несколько иной формы закона был независимо сделан Видманом в 1856 г. и Нейманом и Э. Хагенбахом в 1858 г. (1859, 1860). Хагенбах был первым, кто назвал этот закон законом Пуазейля.

Закон также очень важен в гемореология и гемодинамика, оба поля физиология.^[10]

Позднее, в 1891 г., закон Пуазейля был распространен на турбулентный поток Л. Р. Уилберфорс, основанный на работе Хагенбаха.

Вывод

Уравнение Хагена – Пуазейля может быть получено из Уравнения Навье – Стокса. В ламинарный поток через трубу равномерного (круглого) поперечного сечения, известную как течение Хагена – Пуазейля. Уравнения, описывающие течение Хагена – Пуазейля, могут быть получены непосредственно из Уравнения импульса Навье – Стокса в трехмерных цилиндрических координатах ${ Displaystyle (г, тета, х)}$ сделав следующий набор предположений:

1. Течение устойчивое ( ${ Displaystyle partial (...) / partial t = 0}$ ).
2. Радиальная и азимутальная составляющие скорости жидкости равны нулю ( ${ displaystyle u_ {r} = u _ { theta} = 0}$ ).
3. Течение осесимметричное ( ${ Displaystyle partial (...) / partial theta = 0}$ ).
4. Поток полностью развит (${ displaystyle partial u_ {x} / partial x = 0}$ ). Однако здесь это можно доказать с помощью сохранения массы и сделанных выше предположений.

Тогда угловое уравнение в уравнениях импульса и уравнение неразрывности одинаково удовлетворены. Уравнение радиального импульса сводится к ${ displaystyle partial p / partial r = 0}$, т.е. давление ${ displaystyle p}$ является функцией осевой координаты ${ displaystyle x}$ Только. Для краткости используйте ${ displaystyle u}$ вместо ${ displaystyle u_ {x}}$. Уравнение осевого импульса сводится к

${ displaystyle { frac {1} {r}} { frac { partial} { partial r}} left (r { frac { partial u} { partial r}} right) = { гидроразрыв {1} { mu}} { frac { mathrm {d} p} { mathrm {d} x}}}$

куда ${ displaystyle mu}$ - динамическая вязкость жидкости. В приведенном выше уравнении левая часть является только функцией ${ displaystyle r}$ а член в правой части является только функцией ${ displaystyle x}$, подразумевая, что оба члена должны быть одной и той же константой. Оценить эту константу несложно. Если принять длину трубы равной ${ displaystyle L}$ и обозначим перепад давления между двумя концами трубы через ${ displaystyle Delta p}$ (высокое давление минус низкое давление), то константа просто ${ displaystyle - mathrm {d} p / mathrm {d} x = Delta p / L = G}$ определены так, что ${ displaystyle G}$ положительный. Решение

${ displaystyle u = - { frac {Gr ^ {2}} {4 mu}} + c_ {1} ln r + c_ {2}}$

С ${ displaystyle u}$ должен быть конечным в ${ displaystyle r = 0}$, ${ displaystyle c_ {1} = 0}$. Нет скольжения граничное условие у стенки трубы требует, чтобы ${ displaystyle u = 0}$ в ${ displaystyle r = R}$ (радиус трубы), что дает ${ displaystyle c_ {2} = GR ^ {2} / (4 mu).}$ Таким образом, мы имеем, наконец, следующее параболический скорость профиль:

${ displaystyle u = { frac {G} {4 mu}} (R ^ {2} -r ^ {2}).}$

Максимальная скорость достигается на средней линии трубы (${ displaystyle r = 0}$), ${ displaystyle {u} _ { rm {max}} = GR ^ {2} / (4 mu)}$. Среднюю скорость можно получить интегрированием по трубе поперечное сечение,

${ displaystyle {u} _ { mathrm {avg}} = { frac {1} { pi R ^ {2}}} int _ {0} ^ {R} 2 pi ru mathrm {d} r = { frac {1} {2}} {u} _ { mathrm {max}}.}$

Легко измеримой величиной в эксперименте является объемный расход ${ displaystyle Q = pi R ^ {2} {u} _ { mathrm {avg}}}$. Перестановка этого дает уравнение Хагена – Пуазейля

${ displaystyle Delta p = { frac {8 mu QL} { pi R ^ {4}}}.}$

Тщательный вывод, начиная непосредственно с первых принципов

Хотя более длительный, чем прямое использование Уравнения Навье – Стокса, альтернативный метод вывода уравнения Хагена – Пуазейля заключается в следующем. Поток жидкости по трубе а) Трубка, показывающая воображаемую пластинку. б) Поперечное сечение трубки показывает, как пластинка движется с разной скоростью. Те, кто находится ближе всего к краю трубки, движутся медленно, а те, кто находится рядом с центром, движутся быстро. Предположим, жидкие экспонаты ламинарный поток. Ламинарный поток в круглой трубе предполагает наличие группы круглых слоев (пластин) жидкости, скорость каждого из которых определяется только их радиальным расстоянием от центра трубы. Также предположим, что центр движется быстрее всего, в то время как жидкость, касающаяся стенок трубки, неподвижна (из-за условие противоскольжения ). Чтобы определить движение жидкости, необходимо знать все силы, действующие на каждую пластинку: В давление сила, проталкивающая жидкость через трубку, представляет собой изменение давления, умноженное на площадь: F = −А Δп. Эта сила направлена ​​в направлении движения жидкости. Отрицательный знак происходит от обычного способа определения Δп = пконец − пверх < 0. Вязкость эффекты будут вытягиваться из более быстрой пластинки непосредственно ближе к центру трубки. Вязкость эффекты будут тянуться от более медленной пластинки сразу ближе к стенкам трубки. Вязкость Две жидкости движутся мимо друг друга в Икс направление. Жидкость наверху движется быстрее и будет втягиваться нижней жидкостью в отрицательном направлении, в то время как нижняя жидкость будет втягиваться в положительном направлении верхней жидкостью. Когда два соприкасающихся друг с другом слоя жидкости движутся с разной скоростью, произойдет сдвигающая сила между ними. Эта сила пропорциональный к площадь контакта А, градиент скорости, перпендикулярный направлению потока ΔvИкс/Δу, и константа пропорциональности (вязкость) и определяется выражением ${ displaystyle F _ { text {visacity, top}} = - mu A { frac { Delta v_ {x}} { Delta y}}.}$ Здесь стоит отрицательный знак, потому что нас интересует более быстро движущаяся жидкость (вверху на рисунке), которая замедляется более медленной жидкостью (внизу на рисунке). К Третий закон движения Ньютона, сила, действующая на более медленную жидкость, равна силе, действующей на более быструю жидкость, и противоположна ей (без отрицательного знака). Это уравнение предполагает, что площадь контакта настолько велика, что мы можем игнорировать любые эффекты от краев и что жидкости ведут себя как Ньютоновские жидкости. Более быстрая пластинка Предположим, что мы вычисляем силу, действующую на пластину, с помощью радиус р. Из приведенного выше уравнения нам нужно знать площадь контакта и скорость градиент. Думайте о пластине как о круге радиуса р, толщина доктор, и длина ΔИкс. Площадь контакта между пластиной и более быстрой пластиной - это просто площадь внутренней части цилиндра: А = 2πр ΔИкс. Мы пока не знаем точной формы скорости жидкости внутри трубки, но мы знаем (исходя из нашего предположения выше), что она зависит от радиуса. Следовательно, градиент скорости - это изменение скорости относительно изменения радиуса на пересечении этих двух пластинок. Это перекресток находится в радиусе р. Итак, учитывая, что эта сила будет положительной по отношению к движению жидкости (но производная скорости отрицательна), окончательная форма уравнения станет ${ Displaystyle F _ { text {вязкость, быстро}} = - 2 pi r mu , Delta x , left. { frac {dv} {dr}} right | _ {r}}$ где вертикальная черта и нижний индекс р после производная указывает на то, что его следует брать в радиусе р. Более медленная пластинка Теперь давайте найдем силу сопротивления более медленной пластинки. Нам нужно рассчитать те же значения, что и для силы от более быстрой пластины. В этом случае зона контакта находится на р + доктор вместо р. Кроме того, нам нужно помнить, что эта сила противодействует направлению движения жидкости и поэтому будет отрицательной (а производная скорости отрицательна). ${ Displaystyle F _ { text {вязкость, медленно}} = 2 pi (r + dr) mu , Delta x left. { frac {dv} {dr}} right | _ {r + dr }}$ Собираем все вместе Чтобы найти решение для потока ламинарного слоя через трубку, нам нужно сделать одно последнее предположение. Здесь нет ускорение жидкости в трубе и Первый закон Ньютона, нет чистой силы. Если нет чистой силы, мы можем сложить все силы вместе, чтобы получить ноль. ${ displaystyle 0 = F _ { text {давление}} + F _ { text {вязкость, быстро}} + F _ { text {вязкость, медленно}}}$ или же ${ displaystyle 0 = - Delta p2 pi r , dr-2 pi r mu , Delta x left. { frac {dv} {dr}} right | _ {r} +2 pi (r + dr) mu , Delta x , left. { frac {dv} {dr}} right vert _ {r + dr}.}$ Во-первых, чтобы все происходило в одной и той же точке, используйте первые два члена Расширение ряда Тейлора градиента скорости: ${ displaystyle left. { frac {dv} {dr}} right | _ {r + dr} = left. { frac {dv} {dr}} right | _ {r} + left. { frac {d ^ {2} v} {dr ^ {2}}} right | _ {r} , dr.}$ Выражение справедливо для всех пластинок. Группировка одинаковых членов и удаление вертикальной черты, поскольку предполагается, что все производные находятся на радиусе р, ${ displaystyle 0 = - Delta p2 pi r , dr + 2 pi mu , dr , Delta x { frac {dv} {dr}} + 2 pi r mu , dr , Delta x { frac {d ^ {2} v} {dr ^ {2}}} + 2 pi mu (dr) ^ {2} , Delta x { frac {d ^ {2} v} {dr ^ {2}}}.}$ Наконец, представьте это выражение в виде дифференциальное уравнение, отбрасывая член, квадратичный по доктор. ${ displaystyle { frac {1} { mu}} { frac { Delta p} { Delta x}} = { frac {d ^ {2} v} {dr ^ {2}}} + { frac {1} {r}} { frac {dv} {dr}}}$ Приведенное выше уравнение совпадает с уравнением, полученным из уравнений Навье – Стокса, и вывод отсюда следует, как и ранее.

Запуск потока Пуазейля в трубе

Когда постоянный градиент давления ${ displaystyle G = - mathrm {d} p / mathrm {d} x = { text {constant}}}$ применяется между двумя концами длинной трубы, поток не сразу приобретает профиль Пуазейля, скорее, он развивается со временем и достигает профиля Пуазейля в установившемся состоянии. В Уравнения Навье – Стокса сократить до

${ displaystyle { frac { partial u} { partial t}} = { frac {G} { rho}} + nu left ({ frac { partial ^ {2} u} { partial r ^ {2}}} + { frac {1} {r}} { frac { partial u} { partial r}} right)}$

с начальными и граничными условиями,

${ displaystyle u (r, 0) = 0, quad u (R, t) = 0.}$

Распределение скорости определяется выражением

${ displaystyle u (r, t) = { frac {G} {4 mu}} (R ^ {2} -r ^ {2}) - { frac {2GR ^ {2}} { mu} } sum _ {n = 1} ^ { infty} { frac {1} { lambda _ {n} ^ {3}}} { frac {J_ {o} ( lambda _ {n} r / R)} {J_ {1} ( lambda _ {n})}} e ^ {- lambda _ {n} ^ {2} { frac { nu t} {R ^ {2}}}}, quad J_ {o} ( lambda _ {n}) = 0}$

куда ${ displaystyle J_ {o} ( lambda _ {n} r / R)}$ это Функция Бесселя первого рода нулевого порядка и ${ displaystyle lambda _ {n}}$ положительные корни этой функции и ${ displaystyle J_ {1} ( lambda _ {n})}$ это Функция Бесселя первого рода первого порядка. В качестве ${ Displaystyle т rightarrow infty}$, Раствор Пуазейля восстанавливается.^[11]

Течение Пуазейля в кольцевом сечении

Течение Пуазейля в кольцевом сечении

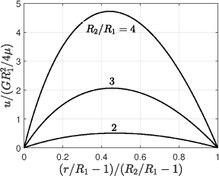
Если ${ displaystyle R_ {1}}$ - радиусы внутреннего цилиндра и ${ displaystyle R_ {2}}$ - радиусы внешнего цилиндра с приложенным градиентом давления между двумя концами ${ displaystyle G = - mathrm {d} p / mathrm {d} x = { text {constant}}}$, распределение скорости и объемный поток через кольцевую трубу равны

${ displaystyle { begin {align} u (r) & = { frac {G} {4 mu}} (R_ {1} ^ {2} -r ^ {2}) + { frac {G} {4 mu}} (R_ {2} ^ {2} -R_ {1} ^ {2}) { frac { ln (r / R_ {1})} { ln (R_ {2} / R_ {1})}}, Q & = { frac {G pi} {8 mu}} left [R_ {2} ^ {4} -R_ {1} ^ {4} - { frac { (R_ {2} ^ {2} -R_ {1} ^ {2}) ^ {2}} { ln R_ {2} / R_ {1}}} right]. End {align}}}$

Когда ${ Displaystyle R_ {2} = R, R_ {1} = 0}$, исходная проблема устранена.^[12]

Течение Пуазейля в трубе с колеблющимся градиентом давления

Поток по трубам с колеблющимся градиентом давления находит применение в кровотоке через крупные артерии.^{[13][14][15][16]} Накладываемый градиент давления определяется выражением

${ Displaystyle { frac { partial p} { partial x}} = - G- alpha cos omega t- beta sin omega t}$

куда ${ displaystyle G}$, ${ displaystyle alpha}$ и ${ displaystyle beta}$ константы и ${ displaystyle omega}$ это частота. Поле скорости определяется выражением

${ displaystyle u (r, t) = { frac {G} {4 mu}} (R ^ {2} -r ^ {2}) + [ alpha F_ {2} + beta (F_ {1 } -1)] { frac { cos omega t} { rho omega}} + [ beta F_ {2} + alpha (F_ {1} -1)] { frac { sin omega т} { rho omega}}}$

куда

${ Displaystyle F_ {1} (kr) = { frac { mathrm {ber} (kr) mathrm {ber} (kR) + mathrm {bei} (kr) mathrm {bei} (kR)} { mathrm {ber} ^ {2} (kR) + mathrm {bei} ^ {2} (kR)}},}$

${ Displaystyle F_ {2} (kr) = { frac { mathrm {ber} (kr) mathrm {bei} (kR) - mathrm {bei} (kr) mathrm {ber} (kR)} { mathrm {ber} ^ {2} (kR) + mathrm {bei} ^ {2} (kR)}},}$

куда ${ displaystyle mathrm {ber}}$ и ${ displaystyle mathrm {bei}}$ являются Функции Кельвина и ${ Displaystyle к ^ {2} = ро омега / му}$.

Плоский поток Пуазейля

Плоский поток Пуазейля

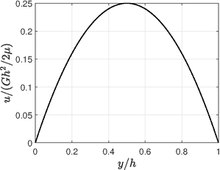
Плоский поток Пуазейля - это поток, создаваемый между двумя бесконечно длинными параллельными пластинами, разделенными расстоянием. ${ displaystyle h}$ с постоянным градиентом давления ${ displaystyle G = - mathrm {d} p / mathrm {d} x = { text {constant}}}$ наносится по направлению потока. Поток по существу однонаправленный из-за бесконечной длины. В Уравнения Навье – Стокса сократить до

${ displaystyle { frac { mathrm {d} ^ {2} u} { mathrm {d} y ^ {2}}} = - { frac {G} { mu}}}$

с условие противоскольжения на обеих стенах

${ displaystyle u (0) = 0, quad u (h) = 0}$

Следовательно, распределение скорости и объемный расход на единицу длины равны

${ displaystyle u (y) = { frac {G} {2 mu}} y (h-y), quad Q = { frac {Gh ^ {3}} {12 mu}}.}$

Поток Пуазейля через некруглые поперечные сечения

Жозеф Буссинеск в 1868 г. получил профиль скорости и объемный расход для прямоугольного канала и труб равностороннего треугольного сечения и для эллиптического сечения.^[17] Джозеф Праудмен получил то же самое для равнобедренных треугольников в 1914 г.^[18] Позволять ${ displaystyle G = - mathrm {d} p / mathrm {d} x = { text {constant}}}$ - постоянный градиент давления, действующий в направлении, параллельном движению.

Скорость и объемный расход в прямоугольном канале высотой ${ Displaystyle 0 Leq Y Leq H}$ и ширина ${ Displaystyle 0 Leq Z Leq L}$ находятся

${ displaystyle { begin {align} u (y, z) & = { frac {G} {2 mu}} y (hy) - { frac {4Gh ^ {2}} { mu pi ^ {3}}} sum _ {n = 1} ^ { infty} { frac {1} {(2n-1) ^ {3}}} { frac { sinh ( beta _ {n} z ) + sinh ( beta _ {n} (lz))} { sinh ( beta _ {n} l)}} sin ( beta _ {n} y), quad beta _ {n} = { frac {(2n-1) pi} {h}}, Q & = { frac {Gh ^ {3} l} {12 mu}} - { frac {16Gh ^ {4}} { pi ^ {5} mu}} sum _ {n = 1} ^ { infty} { frac {1} {(2n-1) ^ {5}}} { frac { cosh ( beta _ {n} l) -1} { sinh ( beta _ {n} l)}}. end {выравнивается}}}$

Скорость и объемный расход трубки с равносторонним треугольным поперечным сечением длины стороны ${ displaystyle 2h / { sqrt {3}}}$ находятся

${ displaystyle { begin {align} u (y, z) & = - { frac {G} {4 mu h}} (yh) (y ^ {2} -3z ^ {2}), Q & = { frac {Gh ^ {4}} {60 { sqrt {3}} mu}}. End {align}}}$

Скорость и объемный расход в прямоугольном равнобедренном треугольнике ${ Displaystyle у = пи, у PM Z = 0}$ находятся

${ displaystyle { begin {align} u (y, z) & = { frac {G} {2 mu}} (y ​​+ z) ( pi -y) - { frac {G} { pi mu}} sum _ {n = 1} ^ { infty} { frac {1} { beta _ {n} ^ {3} sinh (2 pi beta _ {n})}} { sinh [ beta _ {n} (2 pi -y + z)] sin [ beta _ {n} (y + z)] - sinh [ beta _ {n} (y + z) ] sin [ beta _ {n} (yz)] }, quad beta _ {n} = n - { frac {1} {2}}, Q & = { frac {G pi ^ {4}} {12 mu}} - { frac {G} {2 pi mu}} sum _ {n = 1} ^ { infty} { frac {1} { beta _ { n} ^ {5}}} [ coth (2 pi beta _ {n}) + csc (2 pi beta _ {n})]. end {align}}}$

Распределение скорости для труб эллиптического сечения с полуосью ${ displaystyle a}$ и ${ displaystyle b}$ является^[11]

${ displaystyle { begin {align} u (y, z) & = { frac {G} {2 mu left ({ frac {1} {a ^ {2}}} + { frac {1 } {b ^ {2}}} right)}} left (1 - { frac {y ^ {2}} {a ^ {2}}} - { frac {z ^ {2}} {b ^ {2}}} right), Q & = { frac { pi Ga ^ {3} b ^ {3}} {4 mu (a ^ {2} + b ^ {2})}} . end {выравнивается}}}$

Здесь, когда ${ displaystyle a = b}$, Поток Пуазейля для круглой трубы восстанавливается и когда ${ Displaystyle а rightarrow infty}$, самолет Пуазейля поток восстанавливается. Более явные решения с поперечными сечениями, такими как участки в форме улитки, участки, имеющие форму круга с надрезом, следующего за полукругом, кольцевые участки между гомофокальными эллипсами, кольцевые участки между неконцентрическими кругами, также доступны, как описано Ратип Беркер [tr; де ].^[19][20]

Течение Пуазейля через произвольное сечение

Поток через произвольное сечение ${ Displaystyle и (у, г)}$ удовлетворяет условию, что ${ displaystyle u = 0}$ на стенах. Основное уравнение сводится к^[21]

${ displaystyle { frac { partial ^ {2} u} { partial y ^ {2}}} + { frac { partial ^ {2} u} { partial z ^ {2}}} = - { frac {G} { mu}}.}$

Если мы введем новую зависимую переменную как

${ Displaystyle U = U + { гидроразрыва {G} {4 mu}} (y ​​^ {2} + z ^ {2}),}$

то легко видеть, что проблема сводится к интегрированию Уравнение лапласа

${ displaystyle { frac { partial ^ {2} U} { partial y ^ {2}}} + { frac { partial ^ {2} U} { partial z ^ {2}}} = 0 }$

удовлетворяющий условию

${ displaystyle U = { frac {G} {4 mu}} (y ​​^ {2} + z ^ {2})}$

на стене.

Уравнение Пуазейля для идеального изотермического газа

Для сжимаемой жидкости в трубке объемный расход ${ Displaystyle Q (х)}$ (но не массовый расход) и осевая скорость непостоянны вдоль трубы. Расход обычно выражается при давлении на выходе. Когда жидкость сжимается или расширяется, работа выполняется, и жидкость нагревается или охлаждается. Это означает, что скорость потока зависит от теплопередачи к жидкости и от жидкости. Для идеальный газ в изотермический В случае, когда температуре жидкости позволяют уравновеситься с окружающей средой, можно получить приблизительное соотношение для перепада давления.^[22] Используя уравнение состояния идеального газа для процесса с постоянной температурой, соотношение ${ Displaystyle Qp = Q_ {1} p_ {1} = Q_ {2} p_ {2}}$ может быть получен. На коротком участке трубы газ, протекающий по трубе, можно считать несжимаемым, так что закон Пуазейля можно использовать локально,

${ displaystyle - { frac { mathrm {d} p} { mathrm {d} x}} = { frac {8 mu Q} { pi R ^ {4}}} = { frac {8 mu Q_ {2} p_ {2}} { pi pR ^ {4}}}.}.$

Здесь мы предположили, что локальный градиент давления не слишком велик, чтобы оказывать влияние на сжимаемость. Хотя локально мы игнорировали эффекты изменения давления из-за изменения плотности, на больших расстояниях эти эффекты учитываются. С ${ displaystyle mu}$ не зависит от давления, приведенное выше уравнение можно проинтегрировать по длине ${ displaystyle L}$ давать

${ displaystyle p_ {1} ^ {2} -p_ {2} ^ {2} = { frac {16 mu LQ_ {2} p_ {2}} { pi R ^ {4}}}.}$

Следовательно, объемный расход на выходе из трубы определяется выражением

${ displaystyle Q_ {2} = { frac { pi R ^ {4}} {16 mu L}} left ({ frac {p_ {1} ^ {2} -p_ {2} ^ {2 }} {p_ {2}}} right) = { frac { pi R ^ {4} (p_ {1} -p_ {2})} {8 mu L}} { frac {(p_ { 1} + p_ {2})} {2p_ {2}}}.}$

Это уравнение можно рассматривать как закон Пуазейля с дополнительным поправочным коэффициентом. п₁ + п₂/2п₂ выражая среднее давление относительно давления на выходе.

Аналогия электрических схем

Изначально электричество считалось своего рода жидкостью. Этот гидравлическая аналогия все еще концептуально полезен для понимания схем. Эта аналогия также используется для изучения частотной характеристики жидкостно-механических сетей с использованием схемотехнических инструментов, и в этом случае жидкостная сеть называется гидравлический контур. Закон Пуазейля соответствует Закон Ома для электрических цепей, V = ИК. Поскольку результирующая сила, действующая на жидкость, равна ${ Displaystyle Delta F = S Delta p,}$, куда S = πр², т.е. ΔF = πр² Δп, то из закона Пуазейля следует, что

${ displaystyle Delta F = { frac {8 mu LQ} {r ^ {2}}}}$.

Для электрических цепей пусть п - концентрация свободных заряженных частиц (в м⁻³) и разреши q* - заряд каждой частицы (в кулоны ). (Для электронов q* = е = 1.6×10⁻¹⁹ C.) Потом nQ количество частиц в объеме Q, и nQq* это их общий заряд. Это заряд, который протекает через поперечное сечение в единицу времени, т.е. Текущий я. Следовательно, я = nQq*. Как следствие, Q = я/nq*, и

${ displaystyle Delta F = { frac {8 mu LI} {nr ^ {2} q ^ {*}}}.}$

Но ΔF = Уравнение, куда q - полный заряд в объеме трубки. Объем трубки равен πр²L, поэтому количество заряженных частиц в этом объеме равно пπр²L, а их общий заряд ${ displaystyle q = n pi r ^ {2} Lq ^ {*}.}$ Поскольку Напряжение V = EL, то следует

${ displaystyle V = { frac {8 mu LI} {n ^ {2} pi r ^ {4} (q ^ {*}) ^ {2}}}.}$

Это в точности закон Ома, где сопротивление р = V/я описывается формулой

${ displaystyle R = { frac {8 mu L} {n ^ {2} pi r ^ {4} (q ^ {*}) ^ {2}}}}$.

Отсюда следует, что сопротивление р пропорциональна длине L резистора, что верно. Однако также следует, что сопротивление р обратно пропорциональна четвертой степени радиуса р, т.е. сопротивление р обратно пропорциональна второй степени площади поперечного сечения S = πр² резистора, который отличается от электрической формулы. Электрическое соотношение для сопротивления:

${ displaystyle R = { frac { rho L} {S}},}$

куда ρ - удельное сопротивление; т.е. сопротивление р обратно пропорциональна площади поперечного сечения S резистора.^[23] Причина, по которой закон Пуазейля приводит к другой формуле сопротивления р это разница между потоком жидкости и электрическим током. Электронный газ является невязкий, поэтому его скорость не зависит от расстояния до стенок проводника. Сопротивление возникает из-за взаимодействия между текущими электронами и атомами проводника. Следовательно, закон Пуазейля и гидравлическая аналогия полезны только в определенных пределах при применении к электричеству. И закон Ома, и закон Пуазейля иллюстрируют явления переноса.

Применение в медицине - внутривенный доступ и доставка жидкости

Уравнение Хагена – Пуазейля полезно для определения сосудистое сопротивление и, следовательно, расход внутривенные жидкости это может быть достигнуто за счет использования периферийных и центральных канюли. Уравнение утверждает, что скорость потока пропорциональна радиусу в четвертой степени, а это означает, что небольшое увеличение внутреннего диаметра канюли приводит к значительному увеличению скорости потока жидкостей для внутривенного вливания. Радиус канюли для внутривенных вливаний обычно измеряется в "калибровке", которая обратно пропорциональна радиусу. Периферические канюли для внутривенных вливаний обычно доступны в размерах (от больших до малых) 14G, 16G, 18G, 20G, 22G, 26G. Например, поток канюли 14G обычно вдвое больше, чем у канюли 16G, и в десять раз больше, чем у канюли 20G. В нем также указано, что поток обратно пропорционален длине, а это означает, что более длинные линии имеют более низкие скорости потока. Это важно помнить, поскольку в экстренных случаях многие врачи предпочитают более короткие и большие катетеры по сравнению с более длинными и узкими катетерами. Хотя это менее важно с клинической точки зрения, изменение давления может использоваться для увеличения скорости потока путем создания давления в мешке с жидкостью, сжатия мешка или подвешивания мешка выше уровня канюли. Также полезно понимать, что вязкие жидкости будут течь медленнее (например, в переливание крови ).

Смотрите также

• Поток Куэтта
• Закон Дарси
• Пульс
• Волна
• Гидравлический контур

Примечания

Рекомендации

• Sutera, S.P .; Скалак, Р. (1993). «История закона Пуазейля». Ежегодный обзор гидромеханики. 25: 1–19. Bibcode:1993АнРФМ..25 .... 1С. Дои:10.1146 / annurev.fl.25.010193.000245..
• Пфицнер, Дж (1976). «Пуазей и его закон». Анестезия. 31 (2) (опубликовано в марте 1976 г.). С. 273–5. Дои:10.1111 / j.1365-2044.1976.tb11804.x. PMID  779509..
• Bennett, C.O .; Майерс, Дж. Э. (1962). Импульс, тепло и массообмен. Макгроу-Хилл..

внешняя ссылка

• Закон Пуазейля для степенной неньютоновской жидкости
• Закон Пуазейля в слегка сужающейся трубке
• Калькулятор уравнения Хагена – Пуазейля