Невязкое течение - Inviscid flow

Невязкое течение поток невязкой жидкости, в котором вязкость жидкости равна нулю.[1] Хотя есть ограниченные примеры невязких жидкостей, известных как сверхтекучие жидкости, невязкий поток имеет множество применений в динамика жидкостей.[1][2] В Число Рейнольдса невязкого потока приближается к бесконечности, когда вязкость приближается к нулю.[1] Если пренебречь вязкими силами, например в случае невязкого течения, Уравнение Навье-Стокса можно упростить до формы, известной как Уравнение Эйлера.[1] Это упрощенное уравнение применимо к невязкому потоку, а также к потоку с низкой вязкостью и числом Рейнольдса, намного большим единицы.[1] Используя уравнение Эйлера, легко решаются многие задачи гидродинамики, связанные с низкой вязкостью, однако предполагаемая пренебрежимо малая вязкость больше не действует в области жидкости вблизи твердой границы.[3][1][4]

Сама жидкость не обязательно должна иметь нулевую вязкость для возникновения невязкого течения. Также можно организовать течение вязкой жидкости так, чтобы вязкие силы исчезли.[5] Такой поток не имеет вязкого сопротивления своему движению. Эти «невязкие потоки» похожи на вихревые и могут играть ключевую роль в формировании торнадо, то тропический циклон, и турбулентность.

Сверхтекучие жидкости

Дальнейшая информация: Сверхтекучий гелий-4
Сверхтекучий гелий

Сверхтекучая среда - это состояние вещества, в котором наблюдается поток без трения и нулевой вязкости, также известный как невязкий поток.[2]

На сегодняшний день гелий - единственная обнаруженная жидкость, обладающая сверхтекучестью. Гелий становится сверхтекучим, когда он охлаждается до температуры ниже 2,2 К, точки, известной как лямбда-точка.[6] При температурах выше лямбда-точки гелий существует в виде жидкости, демонстрирующей нормальные гидродинамические свойства. Когда он охлаждается до температуры ниже 2,2 К, он начинает проявлять квант поведение. Например, в точке лямбда наблюдается резкое увеличение теплоемкости, по мере того как он продолжает охлаждаться, теплоемкость начинает уменьшаться с температурой.[7] В дополнение теплопроводность очень большой, что способствует отличным охлаждающим свойствам сверхтекучего гелия.[8]

Приложения

Спектрометры хранятся при очень низкой температуре с использованием гелия в качестве хладагента. Это позволяет минимизировать фоновый поток при считывании в далекой инфракрасной области. Некоторые конструкции спектрометров могут быть простыми, но даже корпус имеет самую высокую температуру - менее 20 Кельвинов. Эти устройства обычно не используются, так как использование сверхтекучего гелия по сравнению с другими охлаждающими жидкостями очень дорого.[9]

Большой адронный коллайдер

Сверхтекучий гелий обладает очень высокой теплопроводностью, что делает его очень полезным для охлаждения сверхпроводников. Сверхпроводники, такие как те, что используются на LHC (Большом адронном коллайдере), охлаждаются до температур примерно 1,9 Кельвина. Эта температура позволяет ниобий-титановым магнитам достигать сверхпроводящего состояния. Без использования сверхтекучего гелия эта температура была бы невозможна. Охлаждение до этих температур с помощью этой жидкости - очень дорогая система, и ее немного по сравнению с другими системами охлаждения.[10]

Еще одно применение сверхтекучего гелия - его использование для понимания квантовой механики. Использование лазеров для наблюдения за маленькими капельками позволяет ученым наблюдать за поведением, которое обычно невозможно увидеть. Это связано с тем, что весь гелий в каждой капле находится в одном квантовом состоянии. Это приложение само по себе не имеет практического применения, но помогает нам лучше понять квантовую механику, которая имеет свои собственные приложения.

Число Рейнольдса

Число Рейнольдса (Re) - это безразмерная величина это обычно используется в гидродинамике и инженерии.[11][12] Первоначально описано Джордж Габриэль Стоукс в 1850 году его популяризировали Осборн Рейнольдс в честь кого концепт назвал Арнольд Зоммерфельд в 1908 г.[12][13][14] Число Рейнольдса рассчитывается как:

СимволОписаниеЕдиницы
характерная длинам
скорость жидкостиРС
плотность жидкостикг / м3
вязкость жидкостиПа * с

Значение представляет собой отношение сил инерции к силам вязкости в жидкости и полезно для определения относительной важности вязкости.[11] В невязком потоке, поскольку вязкие силы равны нулю, число Рейнольдса стремится к бесконечности.[1] Когда вязкие силы пренебрежимо малы, число Рейнольдса намного больше единицы.[1] В таких случаях (Re >> 1) предположение о невязком потоке может быть полезно для упрощения многих задач гидродинамики.

Уравнения Эйлера

Этот тип задач гидродинамики может быть описан уравнением Эйлера.
Невязкое обтекание крыла при условии обращение что достигает Условие Кутты

В публикации 1757 г. Леонард Эйлер описал систему уравнений, управляющих невязким потоком:[15]

СимволОписаниеЕдиницы
материальная производная
оператор дель
давлениеПа
вектор ускорения свободного паденияРС2

Предположение о невязком потоке позволяет применять уравнение Эйлера к потокам, в которых вязкие силы незначительны.[1] Некоторые примеры включают обтекание крыла самолета, обтекание опор моста в реке и океанские течения.[1]

Уравнения Навье-Стокса

В 1845 г. Джордж Габриэль Стоукс опубликовал еще одну важную систему уравнений, известную сегодня как Уравнения Навье-Стокса.[1][16] Клод-Луи Навье сначала разработал уравнения, используя молекулярную теорию, которая в дальнейшем была подтверждена Стоксом с использованием теории континуума.[1] Уравнения Навье-Стокса описывают движение жидкостей:[1]

Когда жидкость невязкая или вязкость можно считать незначительной, уравнение Навье-Стокса упрощается до уравнения Эйлера:[1] Это упрощение решить гораздо проще, и его можно применить ко многим типам потоков, в которых вязкость незначительна.[1] Некоторые примеры включают обтекание крыла самолета, обтекание опор моста в реке и океанские течения.[1]

Уравнение Навье-Стокса сводится к уравнению Эйлера, когда . Еще одно условие, приводящее к устранению вязкой силы, - это , и это приводит к «невязкой схеме потока».[5] Обнаружено, что такие течения имеют вихревой характер.

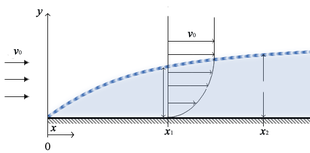
Течение далеко от твердой поверхности раздела, вязкость практически не имеет значения.
Течение на твердой поверхности

Твердые границы

Важно отметить, что пренебрежимо малую вязкость больше нельзя предполагать вблизи твердых границ, например, в случае крыла самолета.[1] В турбулентных режимах потока (Re >> 1) вязкостью обычно можно пренебречь, однако это справедливо только на расстояниях, далеких от границ раздела твердых тел.[1] При рассмотрении потока вблизи твердой поверхности, например потока через трубу или вокруг крыла, удобно разделить на четыре различные области потока вблизи поверхности:[1]

  • Основной турбулентный поток: наиболее удаленный от поверхности вязкостью можно пренебречь.
  • Инерционный подслой: начало основного турбулентного потока, вязкость не имеет большого значения.
  • Буферный слой: преобразование между инерционным и вязким слоями.
  • Вязкий подслой: Ближе к поверхности, здесь важна вязкость.

Хотя эти различия могут быть полезным инструментом для иллюстрации значимости вязких сил вблизи твердых поверхностей раздела, важно отметить, что эти области довольно произвольны.[1] Предположение, что невязкий поток может быть полезным инструментом при решении многих задач гидродинамики, однако это предположение требует тщательного рассмотрения подслоев жидкости, когда речь идет о твердых границах.

Смотрите также

использованная литература

  1. ^ а б c d е ж г час я j k л м п о п q р s т Э., Стюарт, Уоррен; Н., Лайтфут, Эдвин (01.01.2007). Транспортные явления. Вайли. ISBN  9780470115398. OCLC  762715172.
  2. ^ а б С., Стрингари (2016). Конденсация Бозе-Эйнштейна и сверхтекучесть. ISBN  9780198758884. OCLC  936040211.
  3. ^ Клэнси, Л.Дж., Аэродинамика, стр. xviii
  4. ^ Кунду П.К., Коэн И.М. и Ху Х.Х. Механика жидкости, Глава 10, подраздел 1
  5. ^ а б Рунстедтлер, Аллан (2013). "Устройства невязкого потока в динамике жидкости". Международный журнал исследований механики жидкостей. 40 (2): 148–158. Дои:10.1615 / interjfluidmechres.v40.i2.50. ISSN  1064-2277.
  6. ^ «Этот месяц в истории физики». www.aps.org. Получено 2017-03-07.
  7. ^ Ландау, Л. (1941). «Теория сверхтекучести гелия II». Физический обзор. 60 (4): 356–358. Bibcode:1941ПхРв ... 60..356Л. Дои:10.1103 / Physrev.60.356.
  8. ^ "Портал физики природы - оглядываясь назад - плыву по течению - наблюдается сверхтекучесть". www.nature.com. Получено 2017-03-07.
  9. ^ HOUCK, J. R .; УОРД, ДЕННИС (1 января 1979 г.). "Решетчатый спектрометр с охлаждением жидким гелием для астрономических наблюдений в дальней инфракрасной области". Публикации Тихоокеанского астрономического общества. 91 (539): 140–142. Bibcode:1979PASP ... 91..140H. Дои:10.1086/130456. JSTOR  40677459.
  10. ^ «Криогеника: низкие температуры, высокая производительность | ЦЕРН». home.cern. Получено 2017-02-14.
  11. ^ а б Л., Бергман, Теодор; С., Лавин, Адриенн; П., Incropera, Франк; П., Девитт, Дэвид (01.01.2011). Основы тепломассообмена. Вайли. ISBN  9780470501979. OCLC  875769912.
  12. ^ а б Ротт, Н. (28 ноября 2003 г.). «Заметка об истории числа Рейнольдса». Ежегодный обзор гидромеханики. 22 (1): 1–12. Bibcode:1990АнРФМ..22 .... 1Р. Дои:10.1146 / annurev.fl.22.010190.000245.
  13. ^ Рейнольдс, Осборн (1883-01-01). «Экспериментальное исследование обстоятельств, определяющих, будет ли движение воды прямым или извилистым, а также закона сопротивления в параллельных каналах». Философские труды Лондонского королевского общества. 174: 935–982. Bibcode:1883РСПТ..174..935Р. Дои:10.1098 / рстл.1883.0029. ISSN  0261-0523.
  14. ^ Стокс, Г. Г. (1851-01-01). «О влиянии внутреннего трения жидкостей на движение маятников». Труды Кембриджского философского общества. 9: 8. Bibcode:1851TCaPS ... 9 .... 8S.
  15. ^ Эйлер, Леонард (1757). ""Principes généraux de l'état d'équilibre d'un fluide "[Общие принципы состояния равновесия]". Mémoires de l'académie des Sciences de Berlin. 11: 217–273.
  16. ^ Стокс, Г. Г. (1845). "К теориям внутреннего трения движущихся жидкостей, равновесия и движения упругих тел". Proc. Camb. Фил. Soc. 8: 287–319.