Уравнения Эйлера (гидродинамика) - Euler equations (fluid dynamics)

В динамика жидкостей, то Уравнения Эйлера представляют собой набор квазилинейный гиперболические уравнения управляющий адиабатический и невязкий поток. Они названы в честь Леонард Эйлер. Уравнения представляют Уравнения Коши сохранения массы (непрерывности) и баланса импульса и энергии, и может рассматриваться как особый Уравнения Навье – Стокса с нуля вязкость и ноль теплопроводность.[1] Фактически, уравнения Эйлера могут быть получены линеаризацией более точных уравнения неразрывности любить Уравнения Навье – Стокса в состоянии локального равновесия, заданном Максвелловский. Уравнения Эйлера применимы к несжимаемый и чтобы сжимаемый поток - предполагая скорость потока это соленоидальное поле, или используя другое подходящее уравнение энергии соответственно (простейшей формой для уравнений Эйлера является сохранение удельная энтропия ). Исторически Эйлер выводил только уравнения несжимаемой жидкости. Однако в литературе по гидродинамике полный набор, включая уравнение энергии, более общих уравнений сжимаемости часто называют «уравнениями Эйлера».[2]
С математической точки зрения уравнения Эйлера особенно гиперболичны. уравнения сохранения в случае отсутствия внешнего поля (т.е. в пределе высоких Число Фруда ). Фактически, как и любое уравнение Коши, уравнения Эйлера изначально сформулированы в конвективной форме (также называемой "Лагранжева форма ") также можно поместить в" форму сохранения "(также называемую"Эйлерова форма Форма сохранения подчеркивает математическую интерпретацию уравнений как уравнений сохранения через контрольный объем, закрепленный в пространстве, и является наиболее важной для этих уравнений также с числовой точки зрения. Конвективная форма подчеркивает изменения состояния в система отсчета движется с жидкостью.
История
Уравнения Эйлера впервые появились в опубликованной форме в статье Эйлера «Principes généraux du mouvement des fluides», опубликованной в Mémoires de l'Académie des Sciences de Berlin в 1757 г. (в этой статье Эйлер фактически опубликовал только Общее форма уравнения неразрывности и уравнения количества движения;[3] уравнение баланса энергии будет получено столетием позже). Они были среди первых уравнения в частных производных быть записанным. В то время, когда Эйлер опубликовал свою работу, система уравнений состояла из уравнений количества движения и неразрывности и поэтому была недоопределена, за исключением случая несжимаемой жидкости. Дополнительное уравнение, которое позже было названо адиабатическое состояние, был предоставлен Пьер-Симон Лаплас в 1816 г.
Во второй половине XIX века было обнаружено, что уравнение, связанное с балансом энергии, должно всегда соблюдаться, в то время как адиабатическое состояние является следствием основных законов в случае гладких решений. С открытием специальная теория относительности, понятия плотности энергии, плотности импульса и напряжения были объединены в понятие тензор энергии-импульса, энергия и импульс также были объединены в единую концепцию, вектор энергии-импульса[4]
Несжимаемые уравнения Эйлера с постоянной и однородной плотностью
В конвективной форме (т.е. форме с конвективный оператор прямо в уравнение импульса ) несжимаемые уравнения Эйлера в случае постоянной плотности во времени и однородной в пространстве:[5]
где:
- это скорость потока вектор, с компонентами в N-мерное пространство ,
- , для общей функции (или поля) обозначает его материальная производная по времени относительно адвективного поля и
- обозначает градиент относительно пространства,
- обозначает скалярное произведение,
- это оператор набла, здесь используется для обозначения конкретной термодинамической работы градиент (первое уравнение) и
- скорость потока расхождение (второе уравнение),
- является конкретным (в смысле на единицу массы) термодинамическая работа, внутренний исходный термин.
- представляет собой ускорения тела (на единицу массы) действующее на континуум, например сила тяжести, инерционные ускорения, электрическое поле ускорение и так далее.
Первое уравнение - это Уравнение импульса Эйлера с однородной плотностью (для этого уравнения она также не могла быть постоянной во времени). Расширяя материальная производная, уравнения становятся:
Фактически для потока с однородной плотностью имеет место следующее тождество:
где механик давление. Второе уравнение - это несжимаемое ограничение, утверждая, что скорость потока равна соленоидальное поле (порядок уравнений не является причинным, но подчеркивает тот факт, что несжимаемая связь не является вырожденной формой уравнение неразрывности, а скорее уравнения энергии, как это станет ясно из дальнейшего). Примечательно, что уравнение неразрывности потребуется и в этом несжимаемом случае как дополнительное третье уравнение в случае изменения плотности во времени или различающиеся в пространстве. Например, при однородной плотности, но меняющейся во времени, уравнение неразрывности, добавляемое к вышеприведенному набору, будет соответствовать:
Так что случай постоянного и однородная плотность является единственной, не требующей уравнения неразрывности в качестве дополнительного уравнения независимо от наличия или отсутствия несжимаемой связи. Фактически, анализируемый случай несжимаемых уравнений Эйлера с постоянной и однородной плотностью представляет собой игрушечная модель содержит только два упрощенных уравнения, поэтому он идеально подходит для дидактических целей, даже если его физическая значимость ограничена.
Таким образом, приведенные выше уравнения представляют соответственно сохранение массы (1 скалярное уравнение) и импульс (1 векторное уравнение, содержащее скалярные компоненты, где - физическое измерение интересующего пространства). Скорость потока и давление - это так называемые физические переменные.[1]
В системе координат, заданной векторы скорости и внешней силы и есть компоненты и соответственно. Тогда уравнения могут быть записаны в нижних индексах как:
где и нижние индексы обозначают N-мерные космические компоненты, и это Дельта Кренекера. Использование Обозначения Эйнштейна (где сумма подразумевается повторяющимися индексами вместо сигма-обозначение ) также часто.
Свойства
Хотя Эйлер впервые представил эти уравнения в 1755 году, многие фундаментальные вопросы о них остаются без ответа.
В трех измерениях пространства, в некоторых упрощенных сценариях, уравнения Эйлера создают сингулярности. [6]
Гладкие решения свободных (в смысле без источника: g = 0) уравнений удовлетворяют закону сохранения удельной кинетической энергии:
В одномерном случае без источника (как градиента давления, так и внешней силы) уравнение импульса становится невязким Уравнение Бюргерса:
Это модельное уравнение дает много понимания уравнений Эйлера.
Обезразмеривание
Чтобы уравнения были безразмерными, характерная длина , а характеристическая скорость , необходимо определить. Их следует выбирать так, чтобы все безразмерные переменные были первого порядка. Таким образом получаются следующие безразмерные переменные:
и поля единичный вектор:
Подстановка этих обратных соотношений в уравнения Эйлера, определяющие Число Фруда, дает (без * в apix):
Уравнения Эйлера в пределе Фруда (без внешнего поля) называются свободными уравнениями и являются консервативными. Предел высоких чисел Фруда (низкое внешнее поле), таким образом, примечателен и может быть изучен с помощью теория возмущений.
Форма сохранения
Форма сохранения подчеркивает математические свойства уравнений Эйлера, и особенно сжатая форма часто является наиболее удобной для вычислительная гидродинамика симуляции. С точки зрения вычислений, использование сохраняемых переменных дает некоторые преимущества. Это порождает большой класс численных методов, называемых консервативными методами.[1]
В свободные уравнения Эйлера консервативны, в том смысле, что они эквивалентны уравнению сохранения:
или просто в обозначениях Эйнштейна:
где величина сохранения в данном случае вектор, а это поток матрица. Это можно просто доказать.
Во-первых, имеют место следующие тождества:
где обозначает внешний продукт. Те же идентичности, выраженные в Обозначения Эйнштейна находятся:
где я единичная матрица размерностью N и δij ее общий элемент - дельта Кренекера.
Благодаря этим векторным тождествам несжимаемые уравнения Эйлера с постоянной и однородной плотностью и без внешнего поля могут быть помещены в так называемые сохранение (или эйлерова) дифференциальная форма с векторной записью:
или с обозначениями Эйнштейна:
потом несжимаемый Уравнения Эйлера с равномерной плотностью имеют сохраняющие переменные:
Обратите внимание, что во втором компоненте u сам по себе является вектором длины N, поэтому y имеет длину N + 1, а F имеет размер N (N + 1). В 3D, например, y имеет длину 4, I имеет размер 3 × 3, а F имеет размер 4 × 3, поэтому явные формы:
Наконец, уравнения Эйлера можно преобразовать в конкретное уравнение:
Пространственные размеры
Для некоторых задач, особенно когда они используются для анализа сжимаемого потока в воздуховоде или если поток является цилиндрическим или сферически симметричным, одномерные уравнения Эйлера являются полезным первым приближением. Как правило, уравнения Эйлера решаются с помощью Риман с метод характеристик. Это включает в себя поиск кривых на плоскости независимых переменных (т. Е. и ) вдоль которого уравнения в частных производных (PDE) вырождаются в обыкновенные дифференциальные уравнения (ОДУ). Численные решения уравнений Эйлера во многом опираются на метод характеристик.
Несжимаемые уравнения Эйлера
В конвективной форме уравнения Эйлера для несжимаемой жидкости в случае переменной плотности в пространстве имеют вид:[5]
где дополнительные переменные:
- это жидкость плотность вещества,
- это давление, .
Первое уравнение, которое является новым, - это несжимаемая уравнение неразрывности. Фактически, общее уравнение неразрывности будет выглядеть следующим образом:
но здесь последний член тождественно равен нулю для ограничения несжимаемости.
Форма сохранения
Несжимаемые уравнения Эйлера в пределе Фруда эквивалентны одному уравнению сохранения с сохраняющейся величиной и связанным потоком соответственно:
Вот имеет длину и имеет размер .[а] В общем случае (не только в пределе Фруда) уравнения Эйлера выражаются как:
Переменные сохранения
Переменные для уравнений в форме сохранения еще не оптимизированы. Фактически мы могли бы определить:
где:
- это импульс плотность, переменная сохранения.
где:
- это плотность силы, сохраняющая переменная.
Уравнения Эйлера
В дифференциально-конвективной форме сжимаемые (и наиболее общие) уравнения Эйлера можно быстро записать с помощью материальная производная обозначение:
где дополнительные переменные здесь:
- это конкретный внутренняя энергия (внутренняя энергия на единицу массы).
Таким образом, приведенные выше уравнения представляют сохранение массы, импульс, и энергия: уравнение энергии, выраженное в переменной внутренней энергии, позволяет понять связь со случаем несжимаемой жидкости, но не в простейшей форме. плотность массы, скорость потока и давление - это так называемые конвективные переменные (или физические переменные, или лагранжевые переменные), в то время как плотность массы, плотность количества движения и плотность полной энергии являются так называемыми сохраняемые переменные (также называемые эйлеровыми или математическими переменными).[1]
Если указать материальную производную, приведенные выше уравнения будут следующими:
Несжимаемое ограничение (пересмотрено)
Возвращаясь к случаю несжимаемой жидкости, теперь становится очевидным, что несжимаемое ограничение для первых случаев типична особая форма, действующая для несжимаемых течений уравнение энергии, а не массового уравнения. В частности, несжимаемая связь соответствует следующему очень простому уравнению энергии:
Таким образом для несжимаемой невязкой жидкости удельная внутренняя энергия постоянна вдоль линий потока, также в потоке, зависящем от времени. Давление в несжимаемом потоке действует как Множитель Лагранжа, являясь множителем несжимаемой связи в уравнении энергии, и, следовательно, в несжимаемых потоках он не имеет термодинамического смысла. Фактически термодинамика типична для сжимаемых течений и вырождается в несжимаемых.[7]
Основываясь на уравнении сохранения массы, это уравнение можно записать в виде сохранения:
Это означает, что для несжимаемого невязкого непроводящего потока выполняется уравнение неразрывности для внутренней энергии.
Сохранение энтальпии
Поскольку по определению удельная энтальпия равна:
Материальная производная удельной внутренней энергии может быть выражена как:
Тогда, подставляя уравнение импульса в это выражение, получаем:
И, подставив последнее в уравнение энергии, можно получить, что выражение энтальпии для уравнения энергии Эйлера:
В системе отсчета, движущейся с невязким и непроводящим потоком, изменение энтальпии прямо соответствует изменению давления.
Термодинамика идеальных жидкостей
В термодинамика независимыми переменными являются удельный объем, а удельная энтропия, в то время удельная энергия это функция государства этих двух переменных.
Учитывая первое уравнение, переменную необходимо изменить с плотности на удельный объем. По определению:
Таким образом, имеют место следующие тождества:
Затем, подставив эти выражения в уравнение сохранения массы:
И по умножению:
Это уравнение является единственным, принадлежащим общим уравнениям сплошной среды, поэтому только это уравнение имеет такую же форму, например, также в уравнениях Навье-Стокса.
С другой стороны, давление в термодинамике противоположно частной производной удельной внутренней энергии по удельному объему:
поскольку внутренняя энергия в термодинамике является функцией двух вышеупомянутых переменных, градиент давления, содержащийся в уравнении количества движения, должен быть выражен как:
Для краткости удобно поменять обозначения для производных второго порядка:
Наконец, уравнение энергии:
можно дополнительно упростить в конвективной форме, изменив переменную с удельной энергии на удельную энтропию: фактически первый закон термодинамики в местной форме можно написать:
путем подстановки материальной производной внутренней энергии уравнение энергии становится:
теперь член в скобках тождественно равен нулю в соответствии с законом сохранения массы, тогда уравнение энергии Эйлера становится просто:
Следовательно, для термодинамической жидкости уравнения Эйлера сжимаемой жидкости лучше всего записывать как:
где:
- это удельный объем
- - вектор скорости потока
- это удельная энтропия
В общем случае, а не только в случае несжимаемой жидкости, уравнение энергии означает, что для невязкой термодинамической жидкости удельная энтропия постоянна вдоль выкидные линии, также в потоке, зависящем от времени. Основываясь на уравнении сохранения массы, это уравнение можно записать в виде сохранения:[8]
это означает, что для невязкого непроводящего потока выполняется уравнение неразрывности для энтропии.
С другой стороны, две частные производные второго порядка от удельной внутренней энергии в уравнении импульса требуют задания основное уравнение состояния рассматриваемого материала, то есть удельной внутренней энергии как функции двух переменных удельного объема и удельной энтропии:
В фундаментальный уравнение состояния содержит всю термодинамическую информацию о системе (Каллен, 1985),[9] точно так же, как пара тепловой уравнение состояния вместе с калорийность уравнение состояния.
Форма сохранения
Уравнения Эйлера в пределе Фруда эквивалентны одному уравнению сохранения с сохраняющейся величиной и связанным потоком соответственно:
где:
- это импульс плотность, переменная сохранения.
- это полная энергия плотность (общая энергия на единицу объема).
Вот имеет длину N + 2 и имеет размер N (N + 2).[b] В общем случае (не только в пределе Фруда) уравнения Эйлера выражаются как:
где:
- это плотность силы, сохраняющая переменная.
Отметим, что уравнение Эйлера даже в консервативном (отсутствие внешнего поля, предел Фруда) имеет нет Инварианты Римана в общем.[10] Требуются некоторые дополнительные предположения
Однако мы уже упоминали, что для термодинамической жидкости уравнение для полной плотности энергии эквивалентно уравнению сохранения:
Тогда уравнения сохранения в случае термодинамической жидкости проще выразить как:
где:
- - плотность энтропии, термодинамическая переменная сохранения.
Другая возможная форма уравнения энергии, особенно полезная для изобарики, является:
где:
- это общая энтальпия плотность.
Квазилинейная форма и характеристические уравнения
Расширение потоки может быть важной частью строительства числовые решатели, например, используя (приблизительный ) решения Проблема Римана. В регионах, где вектор состояния у изменяется плавно, уравнения в консервативной форме можно записать в квазилинейной форме:
где называются потоком Якобианцы определяется как матрицы:
Очевидно, что этот якобиан не существует в областях разрывов (например, контактных разрывов, ударных волн в невязких непроводящих потоках). Если поток якобианов не являются функциями вектора состояния , уравнения показывает линейный.
Характеристические уравнения
Сжимаемые уравнения Эйлера можно разделить на набор из N + 2 волна уравнения, описывающие звук в континууме Эйлера, если они выражаются в характеристические переменные вместо сохраняемых переменных.
Фактически тензор А является всегда диагонализуемый. Если собственные значения (случай уравнений Эйлера) все действительны, система определена гиперболический, а физически собственные значения представляют скорости распространения информации.[11] Если они все различаются, система определяется строго гиперболический (будет доказано, что это случай одномерных уравнений Эйлера). Кроме того, диагонализация сжимаемого уравнения Эйлера проще, когда уравнение энергии выражается в переменной энтропии (то есть уравнениями для термодинамических жидкостей), чем в других переменных энергии. Это станет ясно при рассмотрении одномерного случая.
Если это правый собственный вектор матрицы соответствующий собственное значение , построив матрица проекции:
Наконец-то можно найти характеристические переменные так как:
поскольку А постоянна, умножая исходное одномерное уравнение в потоково-якобианской форме на п−1 дает характеристические уравнения:[12]
Исходные уравнения были развязанный в N + 2 характеристических уравнения, каждое из которых описывает простую волну, причем собственными значениями являются скорости волны. Переменные шя называются характеристические переменные и являются подмножеством консервативных переменных. Наконец, решение задачи начального значения в терминах характеристических переменных оказывается очень простым. В одном пространственном измерении это:
Затем решение в терминах исходных консервативных переменных получается путем обратного преобразования:
это вычисление может быть выражено как линейная комбинация собственных векторов:
Теперь становится очевидным, что характеристические переменные действуют как веса в линейной комбинации собственных векторов якобиана. Решение можно рассматривать как суперпозицию волн, каждая из которых переносится независимо без изменения формы. Каждый я-я волна имеет форму шяпя и скорость распространения λя. Ниже мы покажем очень простой пример этой процедуры решения.
Волны в одномерной невязкой непроводящей термодинамической жидкости
Если рассматривать уравнения Эйлера для термодинамической жидкости с двумя дополнительными предположениями об одном пространственном измерении и свободном (без внешнего поля: г = 0) :
Если определить вектор переменных:
напоминая, что - удельный объем, скорость потока, удельной энтропии соответствующая матрица якобиана имеет вид:
Сначала нужно найти собственные значения этой матрицы, решив характеристическое уравнение:
это явно:
Эта детерминант очень просто: самое быстрое вычисление начинается с последней строки, так как она имеет наибольшее количество нулевых элементов.
Теперь вычислив определитель 2 × 2:
путем определения параметра:
или, что эквивалентно, в механических переменных, как:
Этот параметр всегда действителен согласно второй закон термодинамики. На самом деле второй закон термодинамики можно выразить несколькими постулатами. Самым элементарным из них в математическом плане является утверждение о выпуклости основного уравнения состояния, т. Е. гессианская матрица удельной энергии, выраженной как функция удельного объема и удельной энтропии:
определяется положительно. Это утверждение соответствует двум условиям:
Первое условие - это то, что обеспечивает параметр а определяется реальным.
В итоге получается характеристическое уравнение:
У этого есть три реальных решения:
Тогда матрица имеет три выделенных действительных собственных значения: одномерные уравнения Эйлера представляют собой строго гиперболическая система.
На этом этапе нужно определить три собственных вектора: каждый получается путем подстановки одного собственного значения в уравнение собственных значений и последующего его решения. Подставляя первое собственное значение λ1 получается:
На основе третьего уравнения, которое просто имеет решение s1= 0, система сводится к:
Два уравнения, как обычно, являются избыточными, тогда собственный вектор определяется с помощью постоянной умножения. Выберем правильный собственный вектор:
Два других собственных вектора могут быть найдены аналогичной процедурой:
Тогда матрицу проекции можно построить:
Наконец становится очевидным, что реальный параметр а ранее определенная скорость распространения информации, характерной для гиперболической системы уравнений Эйлера, т.е. скорость волны. Остается показать, что скорость звука соответствует частному случаю изэнтропическое преобразование:
Сжимаемость и скорость звука
Скорость звука определяется как скорость волны изоэнтропического преобразования:
по определению изоэнтропической сжимаемости:
звуковая скорость всегда вычисляется как квадратный корень из отношения между изоэнтропической сжимаемостью и плотностью:
Идеальный газ
Скорость звука в идеальном газе зависит только от его температуры:
В идеальном газе изоэнтропическое превращение описывается уравнением Закон Пуассона:
где γ это коэффициент теплоемкости, константа для материала. Путем явного указания дифференциалов:
и разделив на ρ−γ dρ:
Тогда при подстановке в общие определения идеального газа изэнтропическая сжимаемость просто пропорциональна давлению:
и результаты скорости звука (Закон Ньютона – Лапласа):
Примечательно, что для идеального газа закон идеального газа считает, что в математической форме это просто:
где п это числовая плотность, и Т это абсолютная температура при условии, что он измеряется в энергетические единицы (т.е. в джоули ) умножением на Постоянная Больцмана. Поскольку массовая плотность пропорциональна числовой плотности через среднее молекулярная масса м материала:
Закон идеального газа можно переформулировать в формуле:
Подставляя это соотношение в закон Ньютона – Лапласа, наконец, достигается выражение скорости звука в идеальном газе как функции температуры.
Поскольку удельная энтальпия в идеальном газе пропорциональна его температуре:
скорость звука в идеальном газе также может зависеть только от его удельной энтальпии:
Теорема Бернулли для установившегося невязкого потока
Теорема Бернулли является прямым следствием уравнений Эйлера.
Несжимаемый падеж и форма Лэмба
В тождество с векторным исчислением из перекрестное произведение локона держит:
где индекс Фейнмана используется, что означает, что индексированный градиент действует только на множитель .
ягненок в своей знаменитой классической книге «Гидродинамика» (1895 г.), которая все еще находится в печати, это тождество использовалось для изменения конвективного члена скорости потока во вращательной форме:[13]
уравнение импульса Эйлера в форме Лэмба принимает следующий вид:
Теперь, исходя из другой идентичности:
уравнение импульса Эйлера принимает форму, оптимальную для демонстрации Теорема Бернулли для установившихся потоков:
Фактически, в случае внешнего консервативное поле, определив его потенциал φ:
В случае установившегося потока производная скорости потока по времени исчезает, поэтому уравнение количества движения принимает следующий вид:
И, проецируя уравнение количества движения на направление потока, т.е. рационализировать, перекрестное произведение исчезает, потому что его результат всегда перпендикулярен скорости:
В случае установившейся несжимаемой жидкости массовое уравнение просто:
- ,
это закон сохранения массы для установившегося потока несжимаемой жидкости утверждает, что плотность вдоль линии тока постоянна. Тогда уравнение импульса Эйлера в стационарном случае несжимаемой жидкости принимает вид:
Удобство определения общая голова для невязкой жидкости поток теперь очевиден:
который можно просто записать как:
Это, баланс количества движения для устойчивого невязкого и несжимаемого потока во внешнем консервативном поле утверждает, что полный напор вдоль линии тока постоянен.
Сжимаемый корпус
В наиболее общем стационарном (сжимаемом) случае массовое уравнение в форме сохранения имеет следующий вид:
- .
Следовательно, предыдущее выражение скорее
Правая часть появляется в уравнении энергии в конвективной форме, которая в установившемся состоянии выглядит так:
Таким образом, уравнение энергии принимает следующий вид:
так что внутренняя удельная энергия теперь присутствует в голове.
Поскольку потенциал внешнего поля обычно мал по сравнению с другими членами, последние удобно сгруппировать в полная энтальпия:
и Инвариант Бернулли для потока невязкого газа составляет:
который можно записать как:
Это, баланс энергии для устойчивого невязкого потока во внешнем консервативном поле утверждает, что сумма полной энтальпии и внешнего потенциала постоянна вдоль линии тока.
В обычном случае малого потенциального поля просто:
Форма Фридмана и форма Крокко
Подставив градиент давления градиентом энтропии и энтальпии, согласно первому закону термодинамики в форме энтальпии:
в конвективной форме уравнения импульса Эйлера получаем:
Фридман вывел это уравнение для частного случая идеальный газ и опубликовал его в 1922 году.[14] Однако это уравнение является общим для невязкой непроводящей жидкости, и оно не подразумевает никакого уравнения состояния.
С другой стороны, подставляя энтальпийную форму первого закона термодинамики во вращательную форму уравнения импульса Эйлера, получаем:
и определив удельную общую энтальпию:
один прибывает в Форма Crocco – Vazsonyi[15] (Crocco, 1937) уравнения импульса Эйлера:
В стационарном случае две переменные энтропия и полная энтальпия особенно полезны, поскольку уравнения Эйлера могут быть преобразованы в форму Крокко:
Наконец, если поток также изотермический:
путем определения конкретной суммы Свободная энергия Гиббса:
Форма Крокко сводится к:
Из этих соотношений можно сделать вывод, что удельная полная свободная энергия однородна в стационарном, безвихревом, изотермическом, изоэнтропическом невязком потоке.
Разрывы
Уравнения Эйлера: квазилинейный гиперболический уравнения и их общие решения волны. При определенных предположениях их можно упростить, что приведет к Уравнение Бюргерса. Подобно знакомому океану волны, волны, описываемые уравнениями Эйлера 'перерыв' и так называемые ударные волны формируются; это нелинейный эффект и представляет собой решение, которое становится многозначный. Физически это представляет собой нарушение предположений, которые привели к формулировке дифференциальных уравнений, и для извлечения дополнительной информации из уравнений мы должны вернуться к более фундаментальной интегральной форме. Потом, слабые решения формулируются путем работы «скачками» (разрывами) в величинах потока - плотности, скорости, давлении, энтропии - с использованием Уравнения Ренкина – Гюгонио. Физические величины редко бывают прерывистыми; в реальных потоках эти разрывы сглаживаются вязкость и по теплопередача. (Увидеть Уравнения Навье – Стокса )
Распространение ударной волны изучается - среди многих других областей - в аэродинамика и ракетный двигатель, где возникают достаточно быстрые потоки.
Чтобы правильно вычислить континуальные величины в разрывных зонах (например, ударных волнах или пограничных слоях) из местный формы[c] (все указанные формы являются локальными формами, поскольку описываемые переменные типичны для одной точки рассматриваемого пространства, т.е. локальные переменные) уравнений Эйлера через методы конечных разностей как правило, для памяти компьютеров сейчас и в ближайшем будущем потребуется слишком много пространственных точек и временных шагов. В этих случаях обязательно избегать локальных форм уравнений сохранения, пропуская некоторые слабые формы, словно конечный том один.
Уравнения Ренкина – Гюгонио
Начиная с простейшего случая, рассмотрим стационарное уравнение свободного сохранения в форме сохранения в пространственной области:
где вообще F - матрица потока. Интегрируя это локальное уравнение по фиксированному объему Vм, это становится:
Затем, исходя из теорема расходимости, мы можем преобразовать этот интеграл в граничный интеграл потока:
Эта глобальная форма просто утверждает, что нет чистого потока сохраняющейся величины, проходящей через область в случае устойчивого и без источника. В 1D объем уменьшается до интервал, граница которого является его экстремумом, то теорема о расходимости сводится к основная теорема исчисления:
это просто конечно-разностное уравнение, известный как отношение скачка:
Это можно сделать явным образом:
где используются следующие обозначения:
Или, если выполнить неопределенный интеграл:
С другой стороны, временное уравнение сохранения:
приводит к соотношению скачка:
Для одномерных уравнений Эйлера переменные сохранения и поток являются векторами:
где:
- - удельный объем,
- поток массы.
В одномерном случае соответствующие соотношения скачков, называемые Уравнения Ренкина – Гюгонио, являются: <[16]
В устойчивом одномерном случае это становится просто:
Благодаря уравнению разности масс уравнение разности энергий можно упростить без каких-либо ограничений:
где - удельная полная энтальпия.
Обычно они выражаются в конвективных переменных:
где:
- скорость потока
- - удельная внутренняя энергия.
Уравнение энергии представляет собой интегральную форму Уравнение Бернулли в сжимаемом корпусе. Прежние уравнения массы и импульса путем подстановки приводят к уравнению Рэлея:
Поскольку второй член является константой, уравнение Рэлея всегда описывает простой линия в плоскость объема давления не зависящие от какого-либо уравнения состояния, т.е. Линия Рэлея. Путем подстановки в уравнения Ренкина – Гюгонио это также можно сделать явным:
Можно также получить кинетическое уравнение и уравнение Гюгонио. Аналитические отрывки здесь для краткости не показаны.
Это соответственно:
Уравнение Гюгонио в сочетании с фундаментальным уравнением состояния материала:
в общем случае описывает в плоскости объема давления кривую, проходящую при условиях (v0, п0), т.е. Кривая Гюгонио, форма которого сильно зависит от типа рассматриваемого материала.
Также принято определять Функция Гюгонио:[17]
позволяя количественно определять отклонения от уравнения Гюгонио, аналогично предыдущему определению гидравлическая головка, полезный для отклонений от уравнения Бернулли.
Форма конечного объема
С другой стороны, интегрируя общее уравнение сохранения:
на фиксированном объеме Vм, а затем на основе теорема расходимости, это становится:
Интегрируя это уравнение также по временному интервалу:
Теперь, определив количество сохраняемых узлов:
мы выводим форму конечного объема:
В частности, для уравнений Эйлера, после определения сохраняющихся величин, конвективные переменные выводятся обратной заменой:
Тогда явные конечные объемные выражения исходных конвективных переменных таковы: <[18]
Ограничения
Было показано, что уравнения Эйлера не являются полной системой уравнений, но они требуют некоторых дополнительных ограничений для получения единственного решения: это уравнение состояния рассматриваемого материала. Чтобы соответствовать термодинамика эти уравнения состояния должны удовлетворять двум законам термодинамики. С другой стороны, по определению неравновесные системы описываются законами, лежащими вне этих законов. Ниже мы перечисляем некоторые очень простые уравнения состояния и соответствующее влияние на уравнения Эйлера.
Идеальный политропный газ
Для идеального политропного газа основной уравнение состояния является:[19]
где - удельная энергия, - удельный объем, - удельная энтропия, молекулярная масса, здесь считается постоянной (политропный процесс ), и можно показать, что они соответствуют коэффициент теплоемкости. Можно показать, что это уравнение согласуется с обычными уравнениями состояния, используемыми в термодинамике.
По термодинамическому определению температуры:
Где температура измеряется в единицах энергии. Сначала обратите внимание, что, объединив эти два уравнения, можно вывести закон идеального газа:
или в обычной форме:
где: - числовая плотность материала. С другой стороны, закон идеального газа менее строг, чем рассматриваемое исходное фундаментальное уравнение состояния.
Теперь рассмотрим молярную теплоемкость, связанную с процессом. Икс:
согласно первому закону термодинамики:
это можно просто выразить как:
Теперь, обращая уравнение для температуры T (e), мы получаем, что для идеального политропного газа изохорная теплоемкость постоянна:
и аналогично для идеального политропного газа изобарная теплоемкость остается постоянной:
Это приводит к двум важным отношения между тепловыми мощностями: постоянная гамма фактически представляет коэффициент теплоемкости в идеальном политропном газе:
и еще один прибывает в Отношение Мейера:
Таким образом, удельная энергия получается путем обращения зависимости T (e):
Удельная энтальпия получается заменой последнего на закон идеального газа:
Из этого уравнения можно вывести уравнение для давления по его термодинамическому определению:
Обращая его, мы приходим к механическому уравнению состояния:
Тогда для идеального газа уравнения Эйлера сжимаемой жидкости можно просто выразить в виде механический или примитивные переменные удельный объем, скорость потока и давление, взяв систему уравнений термодинамической системы и преобразовав уравнение энергии в уравнение давления через это механическое уравнение состояния. Наконец, в конвективной форме они приводят:
и в одномерной квазилинейной форме они приводят:
где консервативная векторная переменная:
и соответствующая матрица якобиана:[21]</ref>[22]
Устойчивый поток в координатах материала
В случае стационарного течения удобно выбрать Кадр Френе-Серре вдоль рационализировать как система координат для описания устойчивого импульс Уравнение Эйлера:[23]
где , и обозначить скорость потока, то давление и плотность соответственно.
Позволять быть Френе-Серре ортонормированный базис который состоит из тангенциального единичного вектора, нормального единичного вектора и бинормального единичного вектора к линии тока соответственно. Поскольку линия тока - это кривая, касательная к вектору скорости потока, левая часть приведенного выше уравнения, конвективная производная скорости, можно описать следующим образом:
где это радиус кривизны обтекаемой формы.
Таким образом, импульсная часть уравнений Эйлера для стационарного течения имеет простой вид:
Для баротропный течь , Уравнение Бернулли выводится из первого уравнения:
Второе уравнение выражает то, что в случае искривления линии тока должна существовать градиент давления нормально к линии тока, потому что центростремительное ускорение из жидкая посылка создается только нормальным градиентом давления.
Третье уравнение выражает, что давление постоянно вдоль оси бинормали.
Теорема обтекаемой кривизны
Позволять - расстояние от центра кривизны линии тока, то второе уравнение записывается следующим образом:
где
Это уравнение гласит:
В постоянном потоке невязкий жидкость без внешних сил центр кривизны линии тока лежит в направлении уменьшения радиального давления.
Хотя эта связь между полем давления и кривизной потока очень полезна, она не имеет названия в англоязычной научной литературе.[24] Японские специалисты по гидродинамике называют это соотношение «теоремой обтекаемой кривизны».[25]
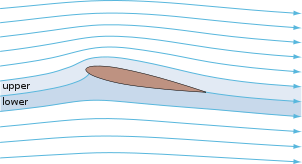
Эта «теорема» ясно объясняет, почему такие низкие давления в центре вихри,[24] которые состоят из концентрических окружностей линий тока, что также позволяет интуитивно объяснить, почему профили подъемные силы.[24]
Точные решения
Все потенциальный поток решения также являются решениями уравнений Эйлера, и в частности уравнений Эйлера несжимаемой жидкости, когда потенциал является гармоническим.[26]

Решения уравнений Эйлера с завихренность находятся:
- параллельно сдвиговые потоки - где поток является однонаправленным, а скорость потока изменяется только в направлениях поперечного потока, например в Декартова система координат поток, например, в -направление - с единственной ненулевой составляющей скорости зависит только от и а не на [27]
- Течение Арнольда – Бельтрами – Чайлдресса - точное решение несжимаемых уравнений Эйлера.
- Два решения трехмерных уравнений Эйлера с цилиндрическая симметрия были представлены Гиббоном, Муром и Стюартом в 2003 году.[28] Эти два решения имеют бесконечную энергию; они взрываются повсюду в пространстве за конечное время.
Смотрите также
- Теорема Бернулли
- Теорема циркуляции Кельвина
- Уравнения Коши
- Уравнения Маделунга
- Число Фруда
- Уравнения Навье – Стокса
- Уравнение Бюргерса
использованная литература
Заметки
- ^ Например, в 3D имеет длину 5, имеет размер 3 × 3 и имеет размер 5 × 3, поэтому явные формы:
- ^ В 3D, например, y имеет длину 5, I имеет размер 3 × 3, а F имеет размер 3 × 5, поэтому явные формы:
- ^ Иногда также называют локальную и глобальную формы соответственно дифференциал и недифференциальный, но это подходит не во всех случаях. Например, это подходит для уравнений Эйлера, в то время как это не подходит для уравнений Навье-Стокса, поскольку в их глобальной форме есть некоторые остаточные пространственные операторы производной первого порядка во всех карактеристических членах переноса, которые в локальной форме содержат пространственные производные.
Цитаты
- ^ а б c d Торо 1999, п. 24.
- ^ Андерсон 1995.
- ^ Эйлер 1757.
- ^ Христодулу 2007.
- ^ а б Охотник 2006.
- ^ arXiv: 1904.04795
- ^ Quartapelle & Auteri 2013, п. 13, гл. 9.
- ^ Ландау и Лифшиц 2013, п. 4, уравнения 2.6 и 2.7.
- ^ Хендерсон 2000, п. 152, 2.6 Термодинамические свойства материалов.
- ^ Чорин и Марсден 2013, п. 118, п. 3.2 Удары.
- ^ Торо 1999, п. 44, п. 2.1. Квазилинейные уравнения.
- ^ Торо 1999, п. 52, п. 2.3 Линейная гиперболическая система.
- ^ Валорани и Насути без даты С. 11–12.
- ^ Фридман 1934, п. 198, уравнение 91.
- ^ Хендерсон 2000, п. 177, п. 2.12 Теорема Крокко.
- ^ Чорин и Марсден 2013, п. 122, п. 3.2 Удары.
- ^ Хендерсон 2000, п. 167, п. 2.96 Теорема Бете – Вейля.
- ^ Quartapelle & Auteri 2013, п. 161, п. 11.10: Forma Difference: metodo dei volumi finiti.
- ^ Quartapelle & Auteri 2013, п. A-61, Приложение E.
- ^ Торо 1999, п. 91, п. 3.1.2. Неконсервативные составы.
- ^ Zingale 2013.
- ^ Торо 1999, п. 92.
- ^ Фэй 1994 С. 150-152.
- ^ а б c Бабинский 2003.
- ^ Имаи 1973.
- ^ Марчиоро и Пульвиренти 1994, п. 33.
- ^ Фридлендер и Серр 2003, п. 298.
- ^ Гиббон, Мур и Стюарт 2003.
Источники
- Андерсон, Джон (1995). Вычислительная гидродинамика. McGraw-Hill Education. ISBN 978-0-07-001685-9.CS1 maint: ref = harv (ссылка на сайт)
- Бабинский, Хольгер (ноябрь 2003 г.), "Как работают крылья?" (PDF), Физическое образование, 38 (6): 497–503, Bibcode:2003PhyEd..38..497B, Дои:10.1088/0031-9120/38/6/001CS1 maint: ref = harv (ссылка на сайт)
- Chorin, Alexandre J .; Марсден, Джерролд Э. (2013). Математическое введение в механику жидкости. Springer. ISBN 978-1-4612-0883-9.CS1 maint: ref = harv (ссылка на сайт)
- Христодулу, Деметриос (октябрь 2007 г.). "Уравнения Эйлера течения сжимаемой жидкости" (PDF). Бюллетень Американского математического общества. 44 (4): 581–602. Дои:10.1090 / S0273-0979-07-01181-0.CS1 maint: ref = harv (ссылка на сайт)
- Эйлер, Леонард (1757). "Principes généraux du mouvement des fluides" [Общие принципы движения жидкостей]. Mémoires de l'académie des Sciences de Berlin (На французском). 11: 274–315.CS1 maint: ref = harv (ссылка на сайт)
- Фэй, Джеймс А. (1994). Введение в механику жидкости. MIT Press. ISBN 978-0-262-06165-0.CS1 maint: ref = harv (ссылка на сайт)
- Friedlander, S .; Серр, Д., ред. (2003). Справочник по математической гидродинамике - Том 2. Эльзевир. ISBN 978-0-444-51287-1.CS1 maint: ref = harv (ссылка на сайт)
- Фридман, А. (1934) [1922]. Кочин Николай (ред.). Опыт гидромеханики сжимаемой жидкости [Очерк гидродинамики сжимаемой жидкости] (по-русски). Петроград.CS1 maint: ref = harv (ссылка на сайт)
- Gibbon, J.D .; Мур, Д.Р .; Стюарт, Дж. (2003). «Точные, бесконечные энергии, взрывающиеся решения трехмерных уравнений Эйлера». Нелинейность. 16 (5): 1823–1831. Bibcode:2003Nonli..16.1823G. Дои:10.1088/0951-7715/16/5/315.CS1 maint: ref = harv (ссылка на сайт)
- Хендерсон, Л.Ф. (2000). «Общие законы распространения ударных волн через вещество». В Бен-Дор, Габи; Игра, Озер; Эльперин, Тов (ред.). Справочник по ударным волнам, набор из трех томов. Эльзевир. ISBN 978-0-08-053372-8.CS1 maint: ref = harv (ссылка на сайт)
- Хантер, Джон К. (25 сентября 2006 г.), Введение в несжимаемые уравнения Эйлера (PDF), получено 2019-05-31CS1 maint: ref = harv (ссылка на сайт)
- 今井 功 (IMAI, Isao) (ноябрь 1973 г.). 『流体力学 (前 編)』 [Гидродинамика 1] (по-японски).裳 華 房 (Шоукабо). ISBN 4-7853-2314-0.
- Ландау, Л. Д.; Лифшиц, Э. М. (2013). Механика жидкости. Эльзевир. ISBN 978-1-4831-4050-6.CS1 maint: ref = harv (ссылка на сайт)
- Марчиоро, С .; Пульвиренти, М. (1994). Математическая теория несжимаемых невязких жидкостей. Прикладные математические науки. 96. Нью-Йорк: Спрингер. ISBN 0-387-94044-8.CS1 maint: ref = harv (ссылка на сайт)
- Quartapelle, Луиджи; Аутери, Франко (2013). Fluidodinamica comprimibile [Динамика сжимаемой жидкости] (на итальянском). CEA. ISBN 978-88-08-18558-7.CS1 maint: ref = harv (ссылка на сайт)
- Торо, Э. Ф. (1999). Решатели Римана и численные методы гидродинамики: практическое введение. Springer. ISBN 978-3-540-65966-2.CS1 maint: ref = harv (ссылка на сайт)
- Валорани, Мауро; Насути, Франческо (без даты), Методы анализа турбомашин (PDF), Sapienza - Universit`a di Roma, получено 2019-05-31CS1 maint: ref = harv (ссылка на сайт)
- Зингейл, М. (16 апреля 2013 г.), Замечания об уравнениях Эйлера (PDF), получено 2019-05-31CS1 maint: ref = harv (ссылка на сайт)
дальнейшее чтение
- Бадин, G .; Кришиани, Ф. (2018). Вариационная формулировка гидродинамики и геофизической гидродинамики - механика, симметрии и законы сохранения -. Springer. п. 218. Дои:10.1007/978-3-319-59695-2. ISBN 978-3-319-59694-5. S2CID 125902566.
- Бэтчелор, Г. К. (1967). Введение в динамику жидкости. Издательство Кембриджского университета. ISBN 0-521-66396-2.
- Томпсон, Филип А. (1972). Поток сжимаемой жидкости. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-064405-5.




























![{ displaystyle { begin {align} u ^ {*} & Equiv { frac {u} {u_ {0}}}, [5pt] r ^ {*} и Equiv { frac {r} {r_ {0}}}, [5pt] t ^ {*} & Equiv { frac {u_ {0}} {r_ {0}}} t, [5pt] p ^ {*} & Equiv { frac {w} {u_ {0} ^ {2}}}, [5pt] nabla ^ {*} & Equiv r_ {0} nabla end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b322da9d688c21acaeafa214b3483985130ec09d)






























![{ Displaystyle left {{ begin {выровнено} {D rho over Dt} & = - rho nabla cdot mathbf {u} [1.2ex] { frac {D mathbf {u }} {Dt}} & = - nabla left ({ frac {p} { rho}} right) + mathbf {g} [1.2ex] {De over Dt} & = - { frac {p} { rho}} nabla cdot mathbf {u} end {align}} right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ac80cc9572c2c8952bdc271f7fafda7b3c087ee)

![{ displaystyle left {{ begin {align} { partial rho over partial t} + mathbf {u} cdot nabla rho + rho nabla cdot mathbf {u} & = 0 [1.2ex] { frac { partial mathbf {u}} { partial t}} + mathbf {u} cdot nabla mathbf {u} + { frac { nabla p} { rho}} & = mathbf {g} [1.2ex] { partial e over partial t} + mathbf {u} cdot nabla e + { frac {p} { rho}} набла cdot mathbf {u} & = 0 end {align}} right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8ac534893cbe0e1656ea3b114a4603425a1eed3)


















![{ Displaystyle left {{ begin {выровнен} {Dv over Dt} & = v nabla cdot mathbf {u} [1.2ex] { frac {D mathbf {u}} {Dt }} & = ve_ {vv} nabla v + ve_ {vs} nabla s + mathbf {g} [1.2ex] {Ds over Dt} & = 0 end {align}} right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a4f5e6ffa04f60e5587f6319189933654c53a5b)


















![{ displaystyle mathbf {P} = left [ mathbf {p} _ {1}, mathbf {p} _ {2}, ..., mathbf {p} _ {n} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32a76df7e0719b77bdae158b5a549b24781cb712)





![{ displaystyle left {{ begin {align} { partial v over partial t} + u { partial v over partial x} -v { partial u over partial x} & = 0 [1.2ex] { partial u over partial t} + u { partial u over partial x} -e_ {vv} v { partial v over partial x} -e_ {vs} v { partial s over partial x} & = 0 [1.2ex] { partial s over partial t} + u { partial s over partial x} & = 0 end {выровнено}} правильно.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395ce1d03d3c9f3102f057bb79e3d59960c6ffbf)










![{ displaystyle left {{ begin {align} e_ {vv} &> 0 [1.2ex] e_ {vv} e_ {ss} -e_ {vs} ^ {2} &> 0 end {выравнивается }}правильно.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c95b8e89f2d859f01c14c0697d666b320d599fe)
































































![{ displaystyle left {{ begin {align} { frac {dx} {dt}} Delta left ({ frac {1} {v}} right) & = Delta j [1.2 пример] { frac {dx} {dt}} Delta j & = Delta left (vj ^ {2} + p right) [1.2ex] { frac {dx} {dt}} Delta E ^ {t} & = Delta left (jv left (E ^ {t} + p right) right) end {align}} right ..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1ce03cab1e469bfeca998e4d7ab5d10d29f5c48)
![{ Displaystyle left {{ begin {выровнено} Delta j & = 0 [1.2ex] Delta left (vj ^ {2} + p right) & = 0 [1.2ex] Delta left (j left ({ frac {E ^ {t}} { rho}} + { frac {p} { rho}} right) right) right) & = 0 end {align}} правильно..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf388d9d9bd5423f57534a27420ae9123413ab27)
![{ Displaystyle left {{ begin {выровнено} Delta j & = 0 [1.2ex] Delta left (vj ^ {2} + p right) & = 0 [1.2ex] Delta h ^ {t} & = 0 end {align}} right.,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6a546f2f73e97b4c864c45f5728ff281dcdc22)

![{ Displaystyle left {{ begin {align} Delta j & = 0 [1.2ex] Delta left ({ frac {u ^ {2}} {v}} + p right) & = 0 [1.2ex] Delta left (e + { frac {1} {2}} u ^ {2} + pv right) & = 0 end {align}} right.,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b7c7fcaf8bd69a72d6d7853f3ee6e44ced26707)

![{ Displaystyle left {{ begin {align} rho u & = rho _ {0} u_ {0} [1.2ex] rho u ^ {2} + p & = rho _ {0} u_ {0} ^ {2} + p_ {0} [1.2ex] e + { frac {1} {2}} u ^ {2} + { frac {p} { rho}} & = e_ { 0} + { frac {1} {2}} u_ {0} ^ {2} + { frac {p_ {0}} { rho _ {0}}} end {align}} right .. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/189de5d7a0780d66568722386b30211f47b83043)
![{ displaystyle left {{ begin {align} u ^ {2} (v, p) & = u_ {0} ^ {2} + left (p-p_ {0} right) left (v_ {0} + v right) [1.2ex] e (v, p) & = e_ {0} + { frac {1} {2}} left (p + p_ {0} right) слева (v_ {0} -v right) end {выровнено}} right ..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b76ecf388380924428a0d917e9924f5b3793aeac)







![{ displaystyle left {{ begin {align} mathbf {u} _ {m, n} & = { frac { mathbf {j} _ {m, n}} { rho _ {m, n }}} [1.2ex] e_ {m, n} & = { frac {E_ {m, n} ^ {t}} { rho _ {m, n}}} - { frac {1} {2}} u_ {m, n} ^ {2} [1.2ex] end {выровнено}} right ..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/822d817fc2ffbf8f27cfa73af7a0bcae37a521b9)
![{ displaystyle left {{ begin {align} rho _ {m, n + 1} & = rho _ {m, n} - { frac {1} {V_ {m}}} int _ {t_ {n}} ^ {t_ {n + 1}} oint _ { partial V_ {m}} rho mathbf {u} cdot { hat {n}} , ds , dt [1.2ex] mathbf {u} _ {m, n + 1} & = mathbf {u} _ {m, n} - { frac {1} { rho _ {m, n} V_ {m} }} int _ {t_ {n}} ^ {t_ {n + 1}} oint _ { partial V_ {m}} ( rho mathbf {u} otimes mathbf {u} -p mathbf {I}) cdot { hat {n}} , ds , dt [1.2ex] mathbf {e} _ {m, n + 1} & = mathbf {e} _ {m, n } - { frac {1} {2}} left (u_ {m, n + 1} ^ {2} -u_ {m, n} ^ {2} right) - { frac {1} { rho _ {m, n} V_ {m}}} int _ {t_ {n}} ^ {t_ {n + 1}} oint _ { partial V_ {m}} left ( rho e + { frac {1} {2}} rho u ^ {2} + p right) mathbf {u} cdot { hat {n}} , ds , dt [1.2ex] end {выровнено }}правильно..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adbf93f77bd84adf21fef81a11ba207200b53a43)

















![{ Displaystyle left {{ begin {выровнен} {Dv over Dt} & = v nabla cdot mathbf {u} [1.2ex] { frac {D mathbf {u}} {Dt }} & = v nabla p + mathbf {g} [1.2ex] {Dp over Dt} & = - gamma p nabla cdot mathbf {u} end {align}} right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc17ce210f9a60fc4e1c71b94fbfffb1bd4b866f)




















