Центр кривизны - Center of curvature

В геометрия, то центр кривизны из кривая находится в точке, находящейся на расстоянии от кривой, равном радиус кривизны лежа на нормальный вектор. Это точка в бесконечности если кривизна нулевая. В соприкасающийся круг к кривой центрируется в центре кривизны. Коши определил центр кривизны C как точка пересечения двух бесконечно близко нормальные линии к кривой.[1] В локус центров кривизны для каждой точки кривой составляют эволюционировать кривой. Этот термин обычно используется в физике применительно к изучению линз и зеркал.
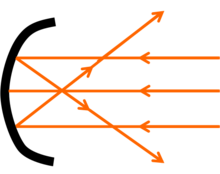
Его также можно определить как сферическое расстояние между точкой, в которой все лучи, падающие на линзу или зеркало, либо сходятся (в случае выпуклых линз и вогнутых зеркал), либо расходятся (в случае вогнутых линз или выпуклые зеркала) и сам объектив / зеркало.[2]
Смотрите также
использованная литература
- ^ *Боровик Александр; Кац, Михаил Г. (2011), «Кто дал вам сказку Коши-Вейерштрасса? Двойственная история строгого исчисления», Основы науки, 17 (3): 245–276, arXiv:1108.2885, Дои:10.1007 / s10699-011-9235-х, S2CID 119320059
- ^ Тринклейн, Фредерик Э. (1992). Современная физика (7-е изд.). Остин: Холт, Райнхарт и Уинстон. ISBN 0-03-074317-6. OCLC 25702491.CS1 maint: дата и год (ссылка на сайт)
Список используемой литературы
- Гильберт, Дэвид; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, ISBN 978-0-8284-0087-9
| Эта связанные с дифференциальной геометрией статья - это заглушка. Вы можете помочь Википедии расширяя это. |
| Эта физика -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
