Завихренность - Vorticity

Часть серии по
Механика сплошной среды
Законы Сохранение Масса Импульс Энергия Неравенства Клаузиус-Дюгем (энтропия)
Механика твердого тела Деформация Эластичность линейный Пластичность Закон Гука Стресс Конечная деформация Бесконечно малая деформация Совместимость Гибка Контактная механика фрикционный Теория разрушения материала Механика разрушения
Гидравлическая механика Жидкости Статика  · Динамика Принцип архимеда  · Принцип Бернулли Уравнения Навье – Стокса Уравнение Пуазейля  · Закон Паскаля Вязкость (Ньютоновский  · неньютоновский ) Плавучесть  · Смешивание  · Давление Жидкости Поверхностное натяжение Капиллярное действие Газы Атмосфера Закон Бойля Закон Чарльза Закон Гей-Люссака Закон о комбинированном газе Плазма
Реология Вязкоупругость Реометрия Реометр Умные жидкости Электрореологический Магнитореологический Феррожидкости
Ученые Бернулли Бойл Коши Чарльз Эйлер Гей-Люссак Гук Ньютон Навье Нолл Паскаль Стокса Truesdell

В механика сплошной среды, завихренность это псевдовектор поле который описывает местный прядение движение континуума около некоторой точки (тенденция чего-то вращаться^[1]), что было бы видно наблюдателю, находящемуся в этой точке и движущемуся вместе с потоком. Это важная величина в динамической теории жидкостей и обеспечивает удобную основу для понимания множества сложных явлений потока, таких как образование и движение вихревые кольца.^[2][3]

Математически завихренность ${ displaystyle { vec { omega}}}$ это завиток из скорость потока ${ displaystyle { vec {u}}}$:^[4][3]

${ Displaystyle { vec { omega}} экв набла раз { vec {u}} ,,}$

где ${ displaystyle nabla}$ это оператор дель. Концептуально, ${ displaystyle { vec { omega}}}$ можно определить, отмечая части континуума в небольшой окрестности рассматриваемой точки и наблюдая за их родственник перемещений по мере их движения по потоку. Завихренность ${ displaystyle { vec { omega}}}$ будет вдвое больше среднего угловая скорость вектор этих частиц относительно их центр массы, ориентированные на правило правой руки.

В двумерный поток, ${ displaystyle { vec { omega}}}$ всегда перпендикулярна плоскости потока и поэтому может считаться скалярное поле.

Примеры

В континууме, который вращается как твердое тело, завихренность вдвое больше угловая скорость вектор этого вращения. Так обстоит дело, например, в центральном ядре Вихрь Ренкина.^[5]

Завихренность может быть отличной от нуля, даже если все частицы движутся прямо и параллельно. пути, Если там есть срезать (то есть, если скорость потока меняется в рационализирует ). Например, в ламинарный поток внутри трубы с постоянным поперечное сечение, все частицы движутся параллельно оси трубы; но быстрее около этой оси и практически неподвижен рядом со стенами. Завихренность будет равна нулю на оси и максимальной у стенок, где сдвиг наибольший.

И наоборот, поток может иметь нулевую завихренность, даже если его частицы движутся по искривленным траекториям. Пример идеальный безвихревой вихрь, где большинство частиц вращаются вокруг некоторой прямой оси со скоростью, обратно пропорциональной их расстоянию до этой оси. Небольшой кусок континуума, который не пересекает ось, будет вращаться в одном смысле, но срезаться в противоположном, так что их средняя угловая скорость об их центре масс равно нулю.

Примеры потоков:
Вихрь, подобный твердому телу v ∝ р	Параллельный поток со сдвигом	Безвихревой вихрь v ∝ 1/р
где v - скорость потока, р - расстояние до центра вихря, а ∝ означает соразмерность. Абсолютные скорости вокруг выделенной точки: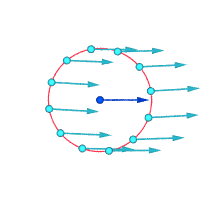
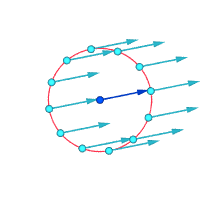
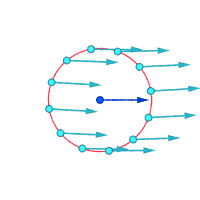
Относительные скорости (увеличены) вокруг выделенной точки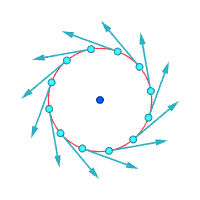
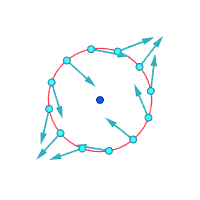
Завихренность ≠ 0	Завихренность ≠ 0	Завихренность = 0

Другой способ визуализировать завихренность - представить, что мгновенно крошечная часть континуума становится твердой, а остальная часть потока исчезает. Если эта крошечная новая твердая частица вращается, а не просто движется вместе с потоком, тогда в потоке есть завихренность. На рисунке ниже левый фрагмент рисунка демонстрирует отсутствие завихренности, а правый фрагмент рисунка демонстрирует наличие завихренности.

Математическое определение

Математически завихренность трехмерного потока представляет собой псевдовекторное поле, обычно обозначаемое как ${ displaystyle { vec { omega}}}$, определяемый как завиток поля скорости ${ displaystyle { vec {v}}}$ описывающий движение континуума. В Декартовы координаты:

${ displaystyle { begin {align} { vec { omega}} = nabla times { vec {v}} & = { begin {pmatrix} { dfrac { partial} { partial x}} & , { dfrac { partial} { partial y}} & , { dfrac { partial} { partial z}} end {pmatrix}} times { begin {pmatrix} v_ {x} & v_ {y} & v_ {z} end {pmatrix}} [6px] & = { begin {pmatrix} { dfrac { partial v_ {z}} { partial y}} - { dfrac { частичный v_ {y}} { partial z}} & quad { dfrac { partial v_ {x}} { partial z}} - { dfrac { partial v_ {z}} { partial x}} & quad { dfrac { partial v_ {y}} { partial x}} - { dfrac { partial v_ {x}} { partial y}} end {pmatrix}} ,. end { выровнено}}}$

На словах завихренность говорит о том, как изменяется вектор скорости, когда человек движется на бесконечно малое расстояние в направлении, перпендикулярном ему.

В двумерном потоке, где скорость не зависит от ${ displaystyle z}$-координат и не имеет ${ displaystyle z}$-компонента, вектор завихренности всегда параллелен ${ displaystyle z}$-ось, и поэтому может быть выражена как скалярное поле, умноженное на постоянный единичный вектор ${ displaystyle { hat {z}}}$:

${ displaystyle { begin {align} { vec { omega}} = nabla times { vec {v}} & = { begin {pmatrix} { dfrac { partial} { partial x}} & , { dfrac { partial} { partial y}} & , { dfrac { partial} { partial z}} end {pmatrix}} times { begin {pmatrix} v_ {x} & v_ {y} & v_ {z} end {pmatrix}} [6px] & = left ({ frac { partial v_ {y}} { partial x}} - { frac { partial v_ { x}} { partial y}} right) { hat {z}} ,. end {align}}}$

Завихренность также связана с величиной потока. обращение (линейный интеграл от скорости) по замкнутой траектории по (классической) Теорема Стокса.^[6] А именно для любых бесконечно малый элемент поверхности C с участием нормальное направление ${ displaystyle { vec {n}}}$ и площадь ${ displaystyle dA}$, тираж ${ displaystyle d Gamma}$ вдоль периметр из ${ displaystyle C}$ это скалярное произведение ${ displaystyle { vec { omega}} cdot ({ vec {n}} , dA)}$ где ${ displaystyle { vec { omega}}}$ завихренность в центре ${ displaystyle C}$.^[6]

Эволюция

Эволюция поля завихренности во времени описывается уравнение завихренности, который можно получить из Уравнения Навье – Стокса.^[7]

Во многих реальных потоках, где вязкостью можно пренебречь (точнее, в потоках с высокой Число Рейнольдса ), поле завихренности может быть смоделировано набором дискретных вихрей, при этом завихренность пренебрежимо мала везде, кроме небольших областей пространства, окружающих оси вихрей. Это верно в случае двумерных потенциальный поток (т.е. двумерный поток с нулевой вязкостью), и в этом случае поле потока можно смоделировать как комплексный поле на комплексная плоскость.

Завихренность - полезный инструмент, позволяющий понять, как идеальные решения для потенциальных потоков могут быть изменены для моделирования реальных потоков. Как правило, наличие вязкости вызывает распространение завихренности от ядер вихря в общее поле течения. Этот поток объясняется диффузионным членом в уравнении переноса завихренности.

Вихревые линии и вихревые трубки

А вихревая линия или линия завихренности - линия, всюду касающаяся вектора локальной завихренности. Линии вихря определяются соотношением^[8]

${ displaystyle { frac {dx} { omega _ {x}}} = { frac {dy} { omega _ {y}}} = { frac {dz} { omega _ {z}}} ,,}$

где ${ displaystyle { vec { omega}} = ( omega _ {x}, omega _ {y}, omega _ {z})}$ вектор завихренности в Декартовы координаты.

А вихревая трубка - поверхность в континууме, образованная всеми вихревыми линиями, проходящими через данную (приводимую) замкнутую кривую в континууме. «Сила» вихревой трубки (также называемой вихревой поток)^[9] представляет собой интеграл завихренности по поперечному сечению трубы и одинаков по всей длине трубы (поскольку завихренность имеет нулевую расходимость). Это следствие Теоремы Гельмгольца (или эквивалентно Теорема циркуляции Кельвина ), что в невязкой жидкости «сила» вихревой трубки также постоянна во времени. Вязкие эффекты приводят к потерям на трение и временной зависимости.

В трехмерном потоке завихренность (измеренная объемный интеграл квадрата его величины) может усиливаться при удлинении вихревой линии - явление, известное как вихревое растяжение.^[10] Это явление возникает при образовании водоворота в ванне в вытекающей воде и нарастании торнадо из-за поднимающихся воздушных потоков.

Измерители завихренности

Пластинчато-вращающийся измеритель завихренности

Пластинчато-вращающийся измеритель завихренности изобрел русский инженер-гидротехник А.Я. Милович (1874–1958). В 1913 году он предложил пробку с четырьмя прикрепленными лопастями как устройство, качественно показывающее величину вертикальной проекции завихренности, и продемонстрировал киносъемку движения поплавка по поверхности воды на модели излучины реки.^[11]

Вихревые измерители с вращающейся лопастью обычно показаны в учебных фильмах по механике сплошных сред (известные примеры включают «Завихренность» NCFMF.^[12] и "Основные принципы потока" Института гидравлических исследований Айовы.^[13]).

Специальные науки

Аэронавтика

В аэродинамика, то поднимать распределение по конечное крыло можно аппроксимировать, если предположить, что каждый сегмент крыла имеет позади себя полубесконечный вихрь. Затем можно определить силу вихрей, используя критерий отсутствия потока, индуцированного через поверхность крыла. Эта процедура называется методом вихревой панели. вычислительная гидродинамика. Затем силы вихрей суммируются, чтобы найти общую приблизительную обращение про крыло. Согласно Теорема Кутты – Жуковского., подъемная сила - это произведение циркуляции, воздушной скорости и плотности воздуха.

Атмосферные науки

В относительная завихренность - завихренность относительно Земли, вызванная полем скорости воздуха. Это поле скорости воздуха часто моделируется как двумерный поток, параллельный земле, так что вектор относительной завихренности обычно представляет собой скалярную величину вращения, перпендикулярную земле. Завихренность положительна, когда - глядя на поверхность земли - ветер вращается против часовой стрелки. В северном полушарии положительная завихренность называется циклоническое вращение, а отрицательная завихренность равна антициклоническое вращение; номенклатура обратная в Южном полушарии.

В абсолютная завихренность вычисляется из скорости воздуха относительно инерциальной системы отсчета и, следовательно, включает член, связанный с вращением Земли, Параметр Кориолиса.

В потенциальная завихренность это абсолютная завихренность, деленная на расстояние по вертикали между уровнями постоянной (потенциальная) температура (или энтропия ). Абсолютная завихренность воздушной массы изменится, если воздушная масса растягивается (или сжимается) в вертикальном направлении, но потенциальная завихренность равна консервированный в адиабатический течь. Так как адиабатический поток преобладает в атмосфере, потенциальная завихренность полезна как приблизительная трассирующий воздушных масс в атмосфере в течение нескольких дней, особенно если смотреть на уровни постоянной энтропии.

В уравнение баротропной завихренности это самый простой способ прогнозирования движения Россби волны (это желоба и гребни из 500гПа геопотенциальная высота ) в течение ограниченного периода времени (несколько дней). В 1950-х годах появились первые успешные программы для численное прогнозирование погоды использовал это уравнение.

В современном модели численного прогноза погоды и модели общей циркуляции (GCM), завихренность может быть одной из предсказанных переменных, и в этом случае соответствующее зависящее от времени уравнение является прогностическое уравнение.

С понятием завихренности относится спиральность ${ displaystyle H (t)}$, определяется как

${ Displaystyle Н (т) = int _ {V} { vec {u}} cdot { vec { omega}} , dV}$

где интеграл по заданному объему ${ displaystyle V}$. В науке об атмосфере важна спиральность движения воздуха при прогнозировании. суперячейки и потенциал для смерч Мероприятия.^[14]

Смотрите также

• Уравнение баротропной завихренности
• Парадокс Даламбера
• Энстрофия
• Потенциал скорости
• Вихрь
• Вихревая трубка
• Вихревое растяжение
• Вихревой
• Подковообразный вихрь
• Вихри крыла

Динамика жидкостей

• Закон Био – Савара
• Тираж
• Уравнения завихренности
• Теорема Кутты – Жуковского.

Атмосферные науки

• Прогностическое уравнение
• Карл-Густав Россби
• Ганс Эртель

использованная литература

Список используемой литературы

• Ачесон, Д.Дж. (1990). Элементарная гидродинамика. Издательство Оксфордского университета. ISBN  0-19-859679-0.
• Ландау, Л. Д .; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN  978-0-08-057073-0.
• Позрикидис, К. (2011). Введение в теоретическую и вычислительную гидродинамику. Издательство Оксфордского университета. ISBN  978-0-19-975207-2.
• Гийон, Этьен; Хулин, Жан-Пьер; Пети, Люк; Митеску, Каталин Д. (2001). Физическая гидродинамика. Издательство Оксфордского университета. ISBN  0-19-851746-7.
• Бэтчелор, Г. К. (2000) [1967], Введение в динамику жидкости, Издательство Кембриджского университета, ISBN  0-521-66396-2
• Клэнси, Л.Дж. (1975), Аэродинамика, Pitman Publishing Limited, Лондон ISBN  0-273-01120-0
• "Глоссарий погоды "The Weather Channel Interactive, Inc .. 2004.
• "Завихренность ". Комплексное издательское дело.

дальнейшее чтение

• Окитани, К. "Элементарный учет завихренности и связанных уравнений". Cambridge University Press. 30 января 2005 г." ISBN  0-521-81984-9
• Чорин, Александр Ж., "Завихренность и турбулентность"Прикладные математические науки, том 103, Springer-Verlag. 1 марта 1994 г." ISBN  0-387-94197-5
• Майда, Эндрю Дж., Андреа Л. Бертоцци "Завихренность и несжимаемый поток". Cambridge University Press; 2002. ISBN  0-521-63948-4
• Триттон, Д. Дж., "Физическая гидродинамика". Ван Ностранд Рейнхольд, Нью-Йорк. 1977. ISBN  0-19-854493-6
• Арфкен, Г. "Математические методы для физиков", 3-е изд. Academic Press, Орландо, Флорида. 1985. ISBN  0-12-059820-5

внешние ссылки

• Вайсштейн, Эрик В. "Завихренность ". Scienceworld.wolfram.com.
• Досуэлл III, Чарльз А. "Праймер по завихренности для применения в суперячейках и торнадо ". Кооперативный институт мезомасштабных метеорологических исследований, Норман, Оклахома.
• Крамер, М. С. "Уравнения Навье – Стокса - Теоремы о переносе завихренности: Введение«Основы механики жидкости».
• Паркер, Дуглас "ENVI 2210 - Атмосфера и динамика океана, 9: Завихренность ". Школа окружающей среды, Университет Лидса. Сентябрь 2001 г.
• Грэм, Джеймс Р., "Астрономия 202: Астрофизическая газовая динамика". Астрономический факультет, Калифорнийский университет в Беркли.
  • "Уравнение завихренности: несжимаемая и баротропная жидкости ".
  • "Интерпретация уравнения завихренности ".
  • "Теорема Кельвина о завихренности для несжимаемого или баротропного потока ".
• "Spherepack 3.1 ". (включает в себя сборник программы завихренности FORTRAN)
• "Мезомасштабное сжимаемое сообщество (MC2)^{[постоянная мертвая ссылка ]} Прогнозы модели в реальном времени". (Анализ потенциальной завихренности)