Curl (математика) - Википедия - Curl (mathematics)

Изображение двумерного векторного поля с равномерным завитком.

В векторное исчисление, то завиток это векторный оператор это описывает бесконечно малый обращение из векторное поле в трехмерном Евклидово пространство. Завиток в точке поля представлен вектор длина и направление которого обозначают величина и ось максимальной циркуляции.^[1] Вихрь поля формально определяется как плотность циркуляции в каждой точке поля.

Векторное поле, ротор которого равен нулю, называется безвихревый. Завиток - это форма дифференциация для векторных полей. Соответствующая форма основная теорема исчисления является Теорема Стокса, что связывает поверхностный интеграл ротора векторного поля к линейный интеграл векторного поля вокруг граничной кривой.

Альтернативная терминология вращение или же вращающийся и альтернативные обозначения $гниль F$ или перекрестное произведение с дель (набла) оператор $\nabla\times F$ иногда используются для $завиток F$ .

в отличие от градиент и расхождение, curl не обобщается просто на другие измерения; немного обобщения возможны, но только в трех измерениях геометрически определенный ротор векторного поля снова является векторным полем. Это явление аналогично трехмерному перекрестное произведение, а связь отражена в обозначениях $\nabla\times$ для локона.

Название «локон» было впервые предложено Джеймс Клерк Максвелл в 1871 г.^[2] но эта концепция, по-видимому, была впервые использована при построении теории оптического поля Джеймс МакКаллах в 1839 г.^[3]^[4]

Определение

Компоненты

F

на позиции

р

, нормальная и касательная к замкнутой кривой

C

в плоскости, охватывающей плоский векторная площадь

{ Displaystyle mathbf {A} = A mathbf { шляпа {п}}}

.

Правило правой руки

Условное обозначение векторной ориентации линейного интеграла

Большой палец указывает в сторону

{ Displaystyle mathbf { шляпа {п}}}

и пальцы сгибаются вдоль ориентации

C

Ротор векторного поля $F$ , обозначаемый $завиток F$ , или же $\nabla \times F$ , или же $гнить F$ , в точке определяется с точки зрения ее проекции на различные прямые, проходящие через точку. Если ${ Displaystyle mathbf { шляпа {п}}}$ - любой единичный вектор, проекция ротора $F$ на ${ Displaystyle mathbf { шляпа {п}}}$ определяется как предельное значение закрытого линейный интеграл в плоскости, ортогональной ${ Displaystyle mathbf { шляпа {п}}}$ делится на замкнутую область, так как путь интегрирования сужается вокруг точки.

Оператор ротора отображает непрерывно дифференцируемые функции $ж : ℝ 3 \to ℝ 3$ к непрерывным функциям $грамм : ℝ 3 \to ℝ 3$ , и, в частности, отображает $C k$ функции в $ℝ 3$ к $C k -1$ функции в $ℝ 3$ .

Неявно curl определяется в точке $п$ в качестве^[5]^[6]

{ displaystyle ( nabla times mathbf {F}) (p) cdot mathbf { hat {n}} { overset { underset { mathrm {def}} {}} {=}} lim _ {A to 0} { frac {1} {| A |}} oint _ {C} mathbf {F} cdot mathrm {d} mathbf {r}}

где линейный интеграл рассчитывается по граница $C$ из площадь $А$ обсуждаемый, $| А |$ величина площади. Это уравнение определяет проекцию ротора $F$ на ${ Displaystyle mathbf { шляпа {п}}}$ . Бесконечно малые поверхности, ограниченные $C$ имеют ${ Displaystyle mathbf { шляпа {п}}}$ как их нормальный. $C$ ориентирована через правило правой руки.

Вышеприведенная формула означает, что ротор векторного поля определяется как бесконечно малый плотность площади из обращение этого поля. Этому определению естественно подходят

то Теорема Кельвина – Стокса, как глобальная формула, соответствующая определению, и
следующее "легко запоминающееся" определение ротора в криволинейном ортогональные координаты, например в Декартовы координаты, сферический, цилиндрический, или даже эллиптический или же параболические координаты:

{ displaystyle { begin {align} & ( operatorname {curl} mathbf {F}) _ {1} = { frac {1} {h_ {2} h_ {3}}} left ({ frac { partial (h_ {3} F_ {3})} { partial u_ {2}}} - { frac { partial (h_ {2} F_ {2})} { partial u_ {3}}} right), [5pt] & ( operatorname {curl} mathbf {F}) _ {2} = { frac {1} {h_ {3} h_ {1}}} left ({ frac { partial (h_ {1} F_ {1})} { partial u_ {3}}} - { frac { partial (h_ {3} F_ {3})} { partial u_ {1}}} right), [5pt] & ( operatorname {curl} mathbf {F}) _ {3} = { frac {1} {h_ {1} h_ {2}}} left ({ frac { partial (h_ {2} F_ {2})} { partial u_ {1}}} - { frac { partial (h_ {1} F_ {1})} { partial u_ {2}}} right). end {align}}}

Уравнение для каждого компонента $(завиток F) k$ могут быть получены заменой каждого вхождения нижнего индекса 1, 2, 3 в циклической перестановке: 1 → 2, 2 → 3 и 3 → 1 (где нижние индексы представляют соответствующие индексы).

Если $(Икс 1, Икс 2, Икс 3)$ являются Декартовы координаты и $(ты 1, ты 2, ты 3)$ - ортогональные координаты, то

{ displaystyle h_ {i} = { sqrt { left ({ frac { partial x_ {1}} { partial u_ {i}}} right) ^ {2} + left ({ frac { partial x_ {2}} { partial u_ {i}}} right) ^ {2} + left ({ frac { partial x_ {3}} { partial u_ {i}}} right) ^ {2}}}}

- длина координатного вектора, соответствующего $ты я$ . Остальные два компонента curl являются результатом циклическая перестановка из индексы: 3,1,2 → 1,2,3 → 2,3,1.

Интуитивная интерпретация

Предположим, что векторное поле описывает поле скорости из поток жидкости (например, большой резервуар жидкость или же газ ), а небольшой шарик находится внутри жидкости или газа (центр шарика закреплен в определенной точке). Если шар имеет шероховатую поверхность, жидкость, протекающая мимо него, заставит его вращаться. Ось вращения (ориентированная согласно правилу правой руки) указывает в направлении завитка поля в центре мяча, а угловая скорость вращения составляет половину величины завитка в этой точке.^[7]

Ротор вектора в любой точке задается вращением бесконечно малой области в ху-самолет (для z-осевая составляющая локона), zx-самолет (для у-осевой компонент локона) и yz-самолет (для Икс-осевая компонента вектора локона). Это хорошо видно на примерах ниже.

использование

На практике приведенное выше определение используется редко, поскольку практически во всех случаях curl оператор может применяться с помощью некоторого набора криволинейные координаты, для которого получены более простые представления.

Обозначение $\nabla \times F$ берет свое начало в сходстве с трехмерным перекрестное произведение, и он полезен как мнемонический в Декартовы координаты если $\nabla$ берется за вектор дифференциальный оператор дель. Такие обозначения с участием операторы распространено в физика и алгебра.

Расширенный в 3-х мерном Декартовы координаты (видеть Del в цилиндрических и сферических координатах за сферический и цилиндрический координатные представления), $\nabla \times F$ это для $F$ состоит из $[F Икс, F у, F z]$ (где нижние индексы указывают на компоненты вектора, а не на частные производные):

{ displaystyle nabla times mathbf {F} = { begin {vmatrix} { boldsymbol { hat { imath}}} & { boldsymbol { hat { jmath}}} & { boldsymbol { шляпа {k}}} [5pt] { dfrac { partial} { partial x}} & { dfrac { partial} { partial y}} и { dfrac { partial} { partial z }} [10pt] F_ {x} & F_ {y} & F_ {z} end {vmatrix}}}

куда $я$ , $j$ , и $k$ являются единичные векторы для $Икс$ -, $у$ -, и $z$ -axes соответственно. Это расширяется следующим образом:^[8]^:43

{ displaystyle nabla times mathbf {F} = left ({ frac { partial F_ {z}} { partial y}} - { frac { partial F_ {y}} { partial z}) } right) { boldsymbol { hat { imath}}} + left ({ frac { partial F_ {x}} { partial z}} - { frac { partial F_ {z}} { partial x}} right) { boldsymbol { hat { jmath}}} + left ({ frac { partial F_ {y}} { partial x}} - { frac { partial F_ { x}} { partial y}} right) { boldsymbol { hat {k}}} = { begin {bmatrix} { frac { partial F_ {z}} { partial y}} - { frac { partial F_ {y}} { partial z}} { frac { partial F_ {x}} { partial z}} - { frac { partial F_ {z}} { partial x }} { frac { partial F_ {y}} { partial x}} - { frac { partial F_ {x}} { partial y}} end {bmatrix}}}

Хотя результат выражается в координатах, результат остается неизменным при правильном повороте осей координат, но результат инвертируется при отражении.

В общей системе координат ротор определяется выражением^[1]

{ displaystyle ( nabla times mathbf {F}) ^ {k} = { frac {1} { sqrt {g}}} varepsilon ^ {k ell m} nabla _ { ell} F_ {м}}

куда $ε$ обозначает Тензор Леви-Чивиты, $\nabla$ то ковариантная производная, ${ displaystyle { sqrt {g}}}$ это якобиан, а Соглашение о суммировании Эйнштейна означает, что повторяющиеся индексы суммируются. Благодаря симметрии символов Кристоффеля, участвующих в ковариантной производной, это выражение сводится к частной производной:

{ displaystyle ( nabla times mathbf {F}) = { frac {1} { sqrt {g}}} mathbf {R} _ {k} varepsilon ^ {k ell m} partial _ {l} F_ {m}}

куда $р k$ - локальные базисные векторы. Эквивалентно, используя внешняя производная локон можно выразить как:

{ displaystyle nabla times mathbf {F} = left ( star { big (} { mathrm {d}} mathbf {F} ^ { flat} { big)} right) ^ { острый }}

Здесь ♭ и ♯ являются музыкальные изоморфизмы, и $★$ это Звездный оператор Ходжа. Эта формула показывает, как рассчитать локон $F$ в любой системе координат, и как расширить локон до любой ориентированный трехмерный Риманов многообразие. Поскольку это зависит от выбора ориентации, curl является хиральный операция. Другими словами, если ориентация меняется на противоположную, то направление завивки также меняется на противоположное.

Примеры

Векторное поле F(x, y) = [y, -x] (слева) и его локон (справа).

Пример 1

В векторное поле

{ displaystyle mathbf {F} (x, y, z) = y { boldsymbol { hat { imath}}} - x { boldsymbol { hat { jmath}}}}

можно разложить как

{ displaystyle mathbf {F} _ {x} = y, mathbf {F} _ {y} = - x, mathbf {F} _ {z} = 0.}

При визуальном осмотре поле можно охарактеризовать как «вращающееся». Если бы векторы поля представляли линейную сила воздействуя на объекты, присутствующие в этой точке, и объект должен был быть помещен внутри поля, объект начинал вращаться вокруг себя по часовой стрелке. Это верно независимо от того, где размещен объект.

Расчет локона:

{ displaystyle nabla times mathbf {F} = 0 { boldsymbol { hat { imath}}} + 0 { boldsymbol { hat { jmath}}} + left ({ frac { partial } { partial x}} (- x) - { frac { partial} { partial y}} y right) { boldsymbol { hat {k}}} = - 2 { boldsymbol { hat { k}}}}

Результирующее векторное поле, описывающее ротор, будет равномерно отрицательно $z$ направление. Результаты этого уравнения совпадают с тем, что можно было предсказать с помощью правило правой руки используя правая система координат. Будучи однородным векторным полем, описанный выше объект будет иметь одинаковую интенсивность вращения независимо от того, где он находится.

Векторное поле F(x, y) = [0, -x²] (слева) и его локон (справа).

Пример 2

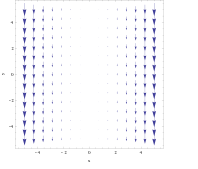
Для векторного поля

{ displaystyle mathbf {F} (x, y, z) = - x ^ {2} { boldsymbol { hat { jmath}}}}

завиток не так очевиден из графика. Однако, если взять объект из предыдущего примера и разместить его в любом месте строки $Икс = 3$ , сила, приложенная к правой стороне, будет немного больше, чем сила, приложенная к левой, заставляя его вращаться по часовой стрелке. Используя правило правой руки, можно предсказать, что полученный локон будет прямым в отрицательном направлении. $z$ направление. И наоборот, если поставить на $Икс = -3$ , объект будет вращаться против часовой стрелки, и правило правой руки приведет к положительному $z$ направление.

Расчет локона:

{ displaystyle { nabla} times mathbf {F} = 0 { boldsymbol { hat { imath}}} + 0 { boldsymbol { hat { jmath}}} + { frac { partial} { partial x}} (- x ^ {2}) { boldsymbol { hat {k}}} = - 2x { boldsymbol { hat {k}}}.}

Локон указывает на негатив $z$ направление, когда $Икс$ положительно и наоборот. В этом поле интенсивность вращения будет больше по мере удаления объекта от плоскости. $Икс = 0$ .

Описательные примеры

В векторном поле, описывающем линейные скорости каждой части вращающегося диска, ротор имеет одинаковое значение во всех точках.
Из четырех Уравнения Максвелла, два-Закон Фарадея и Закон Ампера - можно компактно выразить с помощью curl. Закон Фарадея гласит, что ротор электрического поля равен скорости, противоположной скорости изменения магнитного поля, в то время как закон Ампера связывает ротор магнитного поля с током и скоростью изменения электрического поля.

Идентичности

В целом криволинейные координаты (не только в декартовых координатах) ротор перекрестного произведения векторных полей $v$ и $F$ можно показать как

{ displaystyle nabla times left ( mathbf {v times F} right) = { Big (} left ( mathbf { nabla cdot F} right) + mathbf {F cdot nabla} { Big)} mathbf {v} - { Big (} left ( mathbf { nabla cdot v} right) + mathbf {v cdot nabla} { Big)} mathbf {F} .}

Замена векторного поля $v$ и $\nabla$ оператора, мы приходим к перекрестному произведению векторного поля с ротором векторного поля:

{ Displaystyle mathbf {v times} left ( mathbf { nabla times F} right) = nabla _ { mathbf {F}} left ( mathbf {v cdot F} right ) - left ( mathbf {v cdot nabla} right) mathbf {F} ,}

куда $\nabla F$ обозначение индекса Фейнмана, которое учитывает только изменение, обусловленное векторным полем $F$ (т.е. в этом случае $v$ рассматривается как постоянный в пространстве).

Другой пример - ротор ротора векторного поля. Можно показать, что в общих координатах

{ displaystyle nabla times left ( mathbf { nabla times F} right) = mathbf { nabla} ( mathbf { nabla cdot F}) - nabla ^ {2} mathbf { F} ,}

и это тождество определяет векторный лапласиан из $F$ , обозначается как $\nabla 2 F$ .

Завиток градиент из любой скалярное поле $φ$ всегда нулевой вектор поле

{ Displaystyle набла раз ( набла varphi) = { boldsymbol {0}}}

что следует из антисимметрия в определении локона, а симметрия вторых производных.

Если $φ$ - скалярная функция и $F$ векторное поле, то

{ displaystyle nabla times ( varphi mathbf {F}) = nabla varphi times mathbf {F} + varphi nabla times mathbf {F}}

Обобщения

Операции векторного исчисления град, завиток и div легче всего обобщить в контексте дифференциальных форм, что включает в себя ряд шагов. Короче говоря, они соответствуют производным от 0-форм, 1-форм и 2-форм соответственно. Геометрическая интерпретация локона как вращения соответствует определению бивекторы (2-вектора) в 3-х измерениях с специальная ортогональная алгебра Ли ${ displaystyle { mathfrak {so}}}$ бесконечно малых вращений (в координатах, кососимметричных матриц 3 × 3), в то время как представление поворотов векторами соответствует идентификации 1-векторов (эквивалентно 2-векторам) и ${ displaystyle { mathfrak {so}}}$ , все это трехмерные пространства.

Дифференциальные формы

В трехмерном пространстве дифференциальная 0-форма - это просто функция $ж (Икс, у, z)$ ; дифференциальная 1-форма - это следующее выражение:

{ displaystyle a_ {1} , dx + a_ {2} , dy + a_ {3} , dz;}

дифференциальная 2-форма - это формальная сумма:

{ displaystyle a_ {12} , dx wedge dy + a_ {13} , dx wedge dz + a_ {23} , dy wedge dz;}

а дифференциальная 3-форма определяется одним термином:

{ displaystyle a_ {123} , dx wedge dy wedge dz.}

(Здесь $а$ -коэффициенты - реальные функции; "клинья", например $dx \land dy$ , можно интерпретировать как некие ориентированные элементы области, $dx \land dy = - dy \land dx$ , так далее.)

В внешняя производная из $k$ -форма в $ℝ 3$ определяется как $(k + 1)$ -формировать сверху - и в $ℝ п$ если, например,

{ displaystyle omega ^ {(k)} = sum _ { scriptstyle {i_ {1}

то внешняя производная $d$ приводит к

{ displaystyle d omega ^ {(k)} = sum _ { scriptstyle {j = 1} atop scriptstyle {i_ {1} < cdots

Таким образом, внешняя производная 1-формы является 2-формой, а производная 2-формы - 3-формой. С другой стороны, из-за взаимозаменяемости смешанных производных, например потому что

{ Displaystyle { frac { partial ^ {2}} { partial x , partial y}} = { frac { partial ^ {2}} { partial y , partial x}},}

двукратное применение внешней производной приводит к 0.

Таким образом, обозначая пространство $k$ -формы по $Ω k (ℝ 3)$ а внешнюю производную - на $d$ получается последовательность:

{ displaystyle 0 , { overset {d} { longrightarrow}} , Omega ^ {0} ( mathbf {R} ^ {3}) , { overset {d} { longrightarrow}} , Omega ^ {1} ( mathbf {R} ^ {3}) , { overset {d} { longrightarrow}} , Omega ^ {2} ( mathbf {R} ^ {3}) , { overset {d} { longrightarrow}} , Omega ^ {3} ( mathbf {R} ^ {3}) , { overset {d} { longrightarrow}} , 0.}

Здесь $Ω k (ℝ п)$ это пространство секций внешняя алгебра $Λ k (ℝ п)$ векторный набор более ℝ^п, размерность которого равна биномиальный коэффициент $(п k)$ ; Обратите внимание, что $Ω k (ℝ 3) = 0$ за $k > 3$ или же $k < 0$ . Записывая только размеры, получаем ряд Треугольник Паскаля:

0 → 1 → 3 → 3 → 1 → 0;

одномерные слои соответствуют скалярным полям, а трехмерные слои - векторным полям, как описано ниже. По модулю подходящих отождествлений три нетривиальных вхождения внешней производной соответствуют grad, curl и div.

Дифференциальные формы и дифференциал могут быть определены на любом евклидовом пространстве или на любом многообразии без какого-либо понятия римановой метрики. На Риманово многообразие, или в более общем смысле псевдориманово многообразие, $k$ -формы могут быть идентифицированы с $k$ -вектор поля ( $k$ -формы $k$ -ковекторные поля, а псевдориманова метрика дает изоморфизм между векторами и ковекторами), а на ориентированный векторное пространство с невырожденная форма (изоморфизм между векторами и ковекторами), существует изоморфизм между $k$ -векторы и $(п - k)$ -векторы; в частности, на (касательном пространстве) ориентированного псевдориманова многообразия. Таким образом, на ориентированном псевдоримановом многообразии можно поменять местами $k$ -формы, $k$ -векторные поля, $(п - k)$ -формы и $(п - k)$ -векторные поля; это известно как Двойственность Ходжа. Конкретно на $ℝ 3$ это дается:

1-формы и 1-векторные поля: 1-форма $а Икс dx + а у dy + а z дз$ соответствует векторному полю $(а Икс, а у, а z)$ .
1-формы и 2-формы: одна заменяет $dx$ на двойную величину $dy \land дз$ (т.е. опустить $dx$ ), а также заботясь об ориентации: $dy$ соответствует $дз \land dx = - dx \land дз$ , и $дз$ соответствует $dx \land dy$ . Таким образом, форма $а Икс dx + а у dy + а z дз$ соответствует «двойственной форме» $а z dx \land dy + а у дз \land dx + а Икс dy \land дз$ .

Таким образом, идентификация 0-форм и 3-форм со скалярными полями, а также 1-форм и 2-форм с векторными полями:

grad переводит скалярное поле (0-форма) в векторное поле (1-форма);
curl переводит векторное поле (1-форма) в псевдовекторное поле (2-форма);
div преобразует псевдовекторное поле (2-форма) в псевдоскалярное поле (3-форма)

С другой стороны, тот факт, что $d 2 = 0$ соответствует тождествам

{ Displaystyle набла раз ( набла ф) = 0}

для любого скалярного поля $ж$ , и

{ Displaystyle набла cdot ( набла раз mathbf {v}) = 0}

для любого векторного поля $v$ .

Grad и div обобщаются на все ориентированные псевдоримановы многообразия с той же геометрической интерпретацией, поскольку пространства 0-форм и $п$ -формы всегда (послойно) одномерны и могут быть отождествлены со скалярными полями, в то время как пространства 1-форм и $(п - 1)$ -формы всегда послойны $п$ -мерные и могут быть отождествлены с векторными полями.

Curl не обобщается таким образом до 4 или более измерений (или до 2 или менее измерений); в 4-х измерениях размеры

0 → 1 → 4 → 6 → 4 → 1 → 0;

так что ротор 1-векторного поля (послойно 4-мерного) является 2-векторное поле, послойно 6-мерный,

{ displaystyle omega ^ {(2)} = sum _ {я

который дает сумму шести независимых членов и не может быть отождествлен с 1-векторным полем. Также нельзя осмысленно перейти от 1-векторного поля к 2-векторному полю к 3-векторному полю (4 → 6 → 4), поскольку двукратное взятие дифференциала дает ноль ( $d 2 = 0$ ). Таким образом, не существует ротационной функции из векторных полей в векторные поля в других измерениях, возникающих таким образом.

Однако ротор векторного поля можно определить как 2-векторное поле в общем, как описано ниже.

Завить геометрически

2-вектора соответствуют внешней мощности $Λ 2 V$ ; при наличии внутреннего продукта в координатах это кососимметричные матрицы, которые геометрически рассматриваются как специальная ортогональная алгебра Ли ${ displaystyle { mathfrak {so}}}$ бесконечно малых вращений. Это $(п 2) = .mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px;white-space:nowrap} 1 / 2 п (п - 1)$ размерности, и позволяет интерпретировать дифференциал 1-векторного поля как его бесконечно малые вращения. Только в трех измерениях (или тривиально в 0 измерениях) $п = 1 / 2 п (п - 1)$ , который является наиболее элегантным и распространенным случаем. В двух измерениях ротор векторного поля является не векторным полем, а функцией, так как двухмерные вращения задаются углом (скаляр - требуется ориентация, чтобы выбрать, считать ли вращения по часовой стрелке или против часовой стрелки положительными); это не div, а скорее перпендикулярно ему. В 3-х измерениях ротор векторного поля является векторным полем, как это известно (в 1 и 0 измерениях ротор векторного поля равен 0, потому что нет нетривиальных 2-векторов), тогда как в 4-х измерениях ротор векторное поле геометрически в каждой точке является элементом 6-мерной алгебры Ли ${ displaystyle { mathfrak {so}}}$ .

Ротор трехмерного векторного поля, который зависит только от двух координат (скажем, $Икс$ и $у$ ) представляет собой просто вертикальное векторное поле (в $z$ direction), величина которого является завитком двумерного векторного поля, как в примерах на этой странице.

Рассмотрение curl как 2-векторного поля (антисимметричный 2-тензор) использовалось для обобщения векторного исчисления и связанной с ним физики на более высокие измерения.^[9]

Обратный

В случае, когда расходимость векторного поля $V$ равно нулю, векторное поле $W$ существует такое, что $V = завиток (W)$ .^{[нужна цитата ]} Вот почему магнитное поле, характеризующийся нулевой расходимостью, может быть выражен как ротор магнитный векторный потенциал.

Если $W$ векторное поле с $завиток (W) = V$ , затем добавляем любое поле вектора градиента $град (ж)$ к $W$ приведет к другому векторному полю $W + град (ж)$ такой, что $завиток (W + град (е)) = V$ также. Резюмируя это, можно сказать, что обратный ротор трехмерного векторного поля может быть получен с точностью до неизвестного безвихревое поле с Закон Био – Савара.

Смотрите также

дальнейшее чтение

Корн, Гранино Артур и Тереза М. Корн (январь 2000 г.). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Нью-Йорк: Dover Publications. С. 157–160. ISBN 0-486-41147-8.
Шей, Х. М. (1997). Div, Grad, Curl и все такое: неформальный текст по векторному исчислению. Нью-Йорк: Нортон. ISBN 0-393-96997-5.

внешняя ссылка

"Завиток", Энциклопедия математики, EMS Press, 2001 [1994]
«Векторное исчисление: понимание циркуляции и изгиба - лучше объяснено». betterexplained.com. Получено 2020-11-09.
«Дивергенция и завиток: язык уравнений Максвелла, поток жидкости и многое другое». 21 июня 2018 г. - через YouTube.

[Mathworld-1] а ^б Вайсштейн, Эрик В. "Завиток". MathWorld.

[2] Труды Лондонского математического общества, 9 марта 1871 г.

[3] Собрание сочинений Джеймса МакКаллаха

[4] Самые ранние известные варианты использования некоторых слов математики tripod.com

[5] Математические методы для физики и техники, К.Ф. Райли, М. Хобсон, С.Дж. Бенс, издательство Кембриджского университета, 2010 г., ISBN 978-0-521-86153-3

[6] Векторный анализ (2-е издание), M.R. Spiegel, S. Lipschutz, D. Spellman, Schaum’s Outlines, McGraw Hill (США), 2009, ISBN 978-0-07-161545-7

[7] Гиббс, Джозия Уиллард; Уилсон, Эдвин Бидвелл (1901), Векторный анализ, HDL:2027 / mdp.39015000962285

[8] Арфкен, Джордж Браун (2005). Математические методы для физиков. Вебер, Ханс-Юрген (6-е изд.). Бостон: Эльзевир. ISBN 978-0-08-047069-6. OCLC 127114279.

[9] McDavid, A.W .; Макмаллен, К. Д. (30 октября 2006 г.). «Обобщение перекрестных произведений и уравнений Максвелла на универсальные дополнительные измерения». arXiv:hep-ph / 0609260.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]