Теорема о среднем значении - Mean value theorem

Для любой функции, непрерывной на ${displaystyle [a, b]}$ и дифференцируемый на ${displaystyle (a, b)}$ есть некоторые ${displaystyle c}$ в интервале ${displaystyle (a, b)}$ такая, что секущая, соединяющая концы интервала ${displaystyle [a, b]}$ параллельна касательной в точке ${displaystyle c}$ .

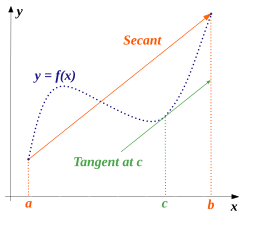
В математика, то теорема о среднем значении утверждает, грубо, что для данной плоской дуга между двумя конечными точками есть хотя бы одна точка, в которой касательная к дуге параллельно секущий через его конечные точки. Это один из самых важных результатов в реальный анализ. Эта теорема используется для доказательства утверждений о функции на интервале, исходя из локальных гипотез о производных в точках интервала.

Точнее, теорема утверждает, что если ${displaystyle f}$ это непрерывная функция на закрытый интервал ${displaystyle [a, b]}$ и дифференцируемый на открытый интервал ${displaystyle (a, b)}$, то существует точка ${displaystyle c}$ в ${displaystyle (a, b)}$ такая, что касательная в c параллельна секущей линии, проходящей через конечные точки ${displaystyle (a, f (a))}$ и ${displaystyle (b, f (b))}$, то есть,

${displaystyle f '(c) = {frac {f (b) -f (a)} {b-a}}.}$

История

Частный случай этого теорема был впервые описан Парамешвара (1370–1460), из Керальская школа астрономии и математики в Индия, в своих комментариях к Говиндасвами и Бхаскара II.^[1] Ограниченная форма теоремы была доказана Мишель Ролль в 1691 г .; в результате получилось то, что сейчас известно как Теорема Ролля, и был доказан только для многочленов, без использования техники исчисления. Теорема о среднем в ее современном виде была сформулирована и доказана Огюстен Луи Коши в 1823 г.^[2]

Официальное заявление

Функция ${displaystyle f}$ достигает наклона секущей между ${displaystyle a}$ и ${displaystyle b}$ как производная в точке ${displaystyle xi in (a, b)}$.

Также возможно наличие нескольких касательных, параллельных секущей.

Позволять ${displaystyle f: [a, b] o mathbb {R}}$ быть непрерывная функция на закрытом интервал ${displaystyle [a, b]}$ , и дифференцируемый на открытом интервале ${displaystyle (a, b)}$, куда ${displaystyle a$. Тогда существует некая ${displaystyle c}$ в ${displaystyle (a, b)}$ такой, что

${displaystyle f '(c) = {frac {f (b) -f (a)} {b-a}}.}$

Теорема о среднем является обобщением Теорема Ролля, что предполагает ${displaystyle f (a) = f (b)}$, так что правая часть выше равна нулю.

Теорема о среднем значении все еще верна в несколько более общем контексте. Достаточно предположить, что ${displaystyle f: [a, b] o mathbb {R}}$ является непрерывный на ${displaystyle [a, b]}$ , и это для каждого ${displaystyle x}$ в ${displaystyle (a, b)}$ то предел

${displaystyle lim _ {h o 0} {frac {f (x + h) -f (x)} {h}}}$

существует как конечное число или равно ${displaystyle infty}$ или же ${displaystyle -infty}$ . Если конечно, этот предел равен ${displaystyle f '(x)}$ . Пример, в котором применяется эта версия теоремы, дается вещественнозначным кубический корень отображение функций ${displaystyle x o x ^ {гидроразрыв {1} {3}}}$ , чей производная стремится к бесконечности в начале координат.

Обратите внимание, что утвержденная теорема неверна, если дифференцируемая функция является комплексной, а не действительной. Например, определите ${displaystyle f (x) = e ^ {xi}}$ для всех реальных ${displaystyle x}$ . потом

${displaystyle f (2pi) -f (0) = 0 = 0 (2pi -0)}$

пока ${displaystyle f '(x) eq 0}$ для любого реального ${displaystyle x}$ .

Эти формальные утверждения также известны как теорема Лагранжа о среднем значении.^[3]

Доказательство

Выражение ${displaystyle {frac {f (b) -f (a)} {(b-a)}}}$ дает склон линии, соединяющей точки ${displaystyle (a, f (a))}$ и ${displaystyle (b, f (b))}$ , который является аккорд графика ${displaystyle f}$ , пока ${displaystyle f '(x)}$ дает наклон касательной к кривой в точке ${displaystyle (x, f (x))}$ . Таким образом, теорема о среднем значении утверждает, что для любой хорды гладкой кривой мы можем найти точку, лежащую между концами хорды, такую, что касательная в этой точке параллельна хорде. Следующее доказательство иллюстрирует эту идею.

Определять ${displaystyle g (x) = f (x) -rx}$ , куда ${displaystyle r}$ является константой. С ${displaystyle f}$ продолжается на ${displaystyle [a, b]}$ и дифференцируемый на ${displaystyle (a, b)}$ , то же самое верно для ${displaystyle g}$ . Теперь мы хотим выбрать ${displaystyle r}$ так что ${displaystyle g}$ удовлетворяет условиям Теорема Ролля. А именно

${displaystyle {egin {выровнено} g (a) = g (b) & iff f (a) -ra = f (b) -rb & iff r (ba) = f (b) -f (a) & iff r = {frac {f (b) -f (a)} {ba}} конец cdot {выровнен}}}$

К Теорема Ролля, поскольку ${displaystyle g}$ дифференцируема и ${displaystyle g (a) = g (b)}$ , существует некоторое ${displaystyle c}$ в ${displaystyle (a, b)}$ для которого ${displaystyle g '(c) = 0}$ , а это следует из равенства ${displaystyle g (x) = f (x) -rx}$ который,

${displaystyle {egin {выровнено} & g '(x) = f' (x) -r & g '(c) = 0 & g' (c) = f '(c) -r = 0 & Rightarrow f' (c ) = r = {frac {f (b) -f (a)} {ba}} конец {выровнено}}}$

Последствия

Теорема 1. Предположим, что ж - непрерывная функция с действительными значениями, определенная на произвольном интервале я реальной линии. Если производная от ж на каждом внутренняя точка интервала я существует и равен нулю, то ж является постоянный в интерьере.

Доказательство: Предположим производную от ж на каждом внутренняя точка интервала я существует и равен нулю. Позволять (а, б) - произвольный открытый интервал в я. По теореме о среднем значении существует точка c в (а,б) такие, что

${displaystyle 0 = f '(c) = {frac {f (b) -f (a)} {b-a}}.}$

Отсюда следует, что ж(а) = ж(б). Таким образом, ж постоянно на внутренней части я и поэтому постоянно на я по преемственности. (См. Ниже многовариантную версию этого результата.)

Примечания:

• Только преемственность ж, не дифференцируемость, нужна на концах интервала я. Гипотезы непрерывности не требуется, если я является открытый интервал, так как наличие производной в точке влечет непрерывность в этой точке. (См. Раздел преемственность и дифференцируемость статьи производная.)
• Дифференцируемость ж можно расслабиться односторонняя дифференцируемость, доказательство приведено в статье о полудифференцируемость.

Теорема 2: если f '(Икс) = грамм'(Икс) для всех Икс в интервале (а, б) области определения этих функций, то f - g постоянно или е = г + с куда c постоянная на (а, б).

Доказательство: Позволять F = f - g, тогда F '= f' - g '= 0 на интервале (а, б), поэтому приведенная выше теорема 1 говорит, что F = f - g это постоянная c или же е = г + с.

Теорема 3: если F является первообразной от ж на интервале я, то самая общая первообразная ж на я является F (x) + c куда c является константой.

Доказательство: Он непосредственно выводится из приведенной выше теоремы 2.

Теорема Коши о среднем значении

Теорема Коши о среднем значении, также известный как расширенная теорема о среднем значении,^[4] является обобщением теоремы о среднем значении. В нем говорится: если функции ж и грамм оба непрерывны на отрезке [а, б] и дифференцируемо на открытом интервале (а, б), то существует c ∈ (а, б), такое что^[3]

Геометрический смысл теоремы Коши

${displaystyle (f (b) -f (a)) g '(c) = (g (b) -g (a)) f' (c).}$

Конечно, если грамм(а) ≠ грамм(б) и если грамм'(c) ≠ 0, это эквивалентно:

${displaystyle {frac {f '(c)} {g' (c)}} = {frac {f (b) -f (a)} {g (b) -g (a)}}.}.}$

Геометрически это означает, что есть касательная к графику изгиб^[5]

${displaystyle {egin {case} [a, b] o mathbf {R} ^ {2} tmapsto (f (t), g (t)) end {case}}}$

который параллельно к линии, определяемой точками (ж(а), грамм(а)) и (ж(б), грамм(б)). Однако теорема Коши не утверждает существования такой касательной во всех случаях, когда (ж(а), грамм(а)) и (ж(б), грамм(б)) являются разными точками, так как это может быть выполнено только для некоторого значения c с f ′(c) = грамм'(c) = 0, другими словами, значение, для которого указанная кривая стационарный; в таких точках вряд ли вообще будет определена касательная к кривой. Примером такой ситуации является кривая, представленная

${displaystyle tmapsto (t ^ {3}, 1-t ^ {2}),}$

который на интервале [−1, 1] идет из точки (−1, 0) в (1, 0), но никогда не имеет горизонтальной касательной; однако у него есть стационарная точка (на самом деле куспид ) в т = 0.

Теорема Коши о среднем значении может быть использована для доказательства Правило л'Опиталя. Теорема о среднем значении является частным случаем теоремы Коши о среднем значении, когда грамм(т) = т.

Доказательство теоремы Коши о среднем значении

Доказательство теоремы Коши о среднем значении основано на той же идее, что и доказательство теоремы о среднем значении.

• Предполагать грамм(а) ≠ грамм(б). Определять час(Икс) = ж(Икс) − rg(Икс), куда р фиксируется таким образом, что час(а) = час(б), а именно

${displaystyle {egin {выровнено} h (a) = h (b) & iff f (a) -rg (a) = f (b) -rg (b) & iff r (g (b) -g (a)) = f (b) -f (a) & тогда и только тогда, когда r = {frac {f (b) -f (a)} {g (b) -g (a)}}. end {align}}}$

С ж и грамм продолжаются на [а, б] и дифференцируемо на (а, б), то же верно и для час. В целом, час удовлетворяет условиям Теорема Ролля: следовательно, есть некоторые c в (а, б) для которого час'(c) = 0. Теперь, используя определение час у нас есть:

${displaystyle 0 = h '(c) = f' (c) -rg '(c) = f' (c) -left ({frac {f (b) -f (a)} {g (b) -g) (a)}} ight) g '(c).}$

Следовательно:

${displaystyle f '(c) = {frac {f (b) -f (a)} {g (b) -g (a)}} g' (c),}$

откуда и следует результат.^[3]

• Если грамм(а) = грамм(б), то применяя Теорема Ролля к грамм, следует, что существует c в (а, б) для которого грамм'(c) = 0. Используя этот выбор c, Теорема Коши о среднем значении (тривиально) верна.

Обобщение для детерминант

Предположить, что ${displaystyle f, g,}$ и ${displaystyle h}$ дифференцируемые функции на ${displaystyle (a, b)}$ которые продолжаются ${displaystyle [a, b]}$. Определять

${displaystyle D (x) = left | {egin {array} {ccc} f (x) & g (x) & h (x) f (a) & g (a) & h (a) f (b) & g (b) ) & h (b) end {array}} ight |}$

Существует ${displaystyle cin (a, b)}$ такой, что ${displaystyle D '(c) = 0}$.

Заметь

${displaystyle D '(x) = left | {egin {array} {ccc} f' (x) & g '(x) & h' (x) f (a) & g (a) & h (a) f (b) ) & g (b) & h (b) end {array}} ight |}$

и если мы разместим ${displaystyle h (x) = 1}$, получаем теорему Коши о среднем значении. Если мы разместим ${displaystyle h (x) = 1}$ и ${displaystyle g (x) = x}$ мы получили Теорема Лагранжа о среднем значении.

Доказательство обобщения довольно просто: каждое из ${displaystyle D (a)}$ и ${displaystyle D (b)}$ - определители с двумя одинаковыми строками, поэтому ${displaystyle D (a) = D (b) = 0}$. Из теоремы Ролля следует, что существует ${displaystyle cin (a, b)}$ такой, что ${displaystyle D '(c) = 0}$.

Теорема о среднем значении нескольких переменных

Теорема о среднем значении обобщается на реальные функции нескольких переменных. Уловка состоит в том, чтобы использовать параметризацию для создания реальной функции одной переменной, а затем применить теорему об одной переменной.

Позволять ${displaystyle G}$ - открытое выпуклое подмножество ${displaystyle mathbb {R} ^ {n}}$ , и разреши ${displaystyle f: G o mathbb {R}}$ - дифференцируемая функция. Исправить точки ${displaystyle x, yin G}$ , и определим ${displaystyle g (t) = f {Big (} (1-t) x + ty {Big)}}$ . С ${displaystyle g}$ является дифференцируемой функцией от одной переменной, теорема о среднем дает:

${displaystyle g (1) -g (0) = g '(c)}$

для некоторых ${displaystyle c}$ от 0 до 1. Но поскольку ${displaystyle g (1) = f (y)}$ и ${displaystyle g (0) = f (x)}$ , вычисление ${displaystyle g '(c)}$ явно мы имеем:

${displaystyle f (y) -f (x) = abla f {Big (} (1-c) x + cy {Big)} cdot (y-x)}$

куда ${displaystyle abla}$ обозначает градиент и ${displaystyle cdot}$ а скалярное произведение. Заметим, что это точный аналог теоремы с одной переменной (в случае ${displaystyle n = 1}$ это является теорема с одной переменной). Посредством Неравенство Коши – Шварца, уравнение дает оценку:

${displaystyle {Bigg |} f (y) -f (x) {Bigg |} leq {Bigg |} abla f {Big (} (1-c) x + cy {Big)} {Bigg |} {Big |} yx {Большой |}.}$

В частности, когда частные производные от ${displaystyle f}$ ограничены, ${displaystyle f}$ является Липшицева непрерывная (и поэтому равномерно непрерывный ).

В качестве приложения к вышесказанному, мы доказываем, что ${displaystyle f}$ постоянно, если ${displaystyle G}$ открыта и связана, и каждая частная производная от ${displaystyle f}$ равно 0. Выберите какую-нибудь точку ${displaystyle x_ {0} в G}$ , и разреши ${displaystyle g (x) = f (x) -f (x_ {0})}$ . Мы хотим показать ${displaystyle g (x) = 0}$ для каждого ${displaystyle xin G}$ . Для этого пусть ${displaystyle E = {xin G: g (x) = 0}}$ . потом E закрыто и непусто. Он тоже открыт: для всех ${displaystyle xin E}$ ,

${displaystyle {Big |} g (y) {Big |} = {Bigg |} g (y) -g (x) {Bigg |} leq (0) {Big |} y-x {Big |} = 0}$

для каждого ${displaystyle y}$ в каком-то районе ${displaystyle x}$ . (Здесь важно, чтобы ${displaystyle x}$ и ${displaystyle y}$ достаточно близки друг к другу.) Поскольку ${displaystyle G}$ связано, заключаем ${displaystyle E = G}$ .

Вышеупомянутые аргументы сделаны безкоординатным способом; следовательно, они обобщаются на случай, когда ${displaystyle G}$ является подмножеством банахова пространства.

Теорема о среднем значении для векторных функций

Точного аналога теоремы о среднем для векторных функций не существует.

В Принципы математического анализа, Рудин дает неравенство, которое можно применить ко многим из тех же ситуаций, к которым применима теорема о среднем значении в одномерном случае:^[6]

Теорема. Для непрерывной векторнозначной функции ${displaystyle mathbf {f}: [a, b] o mathbb {R} ^ {k}}$ дифференцируемый на ${displaystyle (a, b)}$, Существует ${displaystyle xin (a, b)}$ такой, что ${displaystyle | mathbf {f} '(x) | geq {frac {1} {b-a}} | mathbf {f} (b) -mathbf {f} (a) |}$.

Жан Дьедонне в его классическом трактате Основы современного анализа отбрасывает теорему о среднем значении и заменяет ее неравенством среднего значения, поскольку доказательство неконструктивно, и нельзя найти среднее значение, а в приложениях требуется только неравенство среднего значения. Серж Ланг в Анализ I использует теорему о среднем значении в интегральной форме как мгновенный рефлекс, но это использование требует непрерывности производной. Если использовать Интеграл Хенстока – Курцвейла можно иметь теорему о среднем значении в интегральной форме без дополнительного предположения, что производная должна быть непрерывной, поскольку каждая производная интегрируема по Хенстоку – Курцвейлу. Проблема в следующем: если ж : U → р^м - дифференцируемая функция (где U ⊂ р^п открыто) и если Икс + th, х, ч ∈ р^п, т ∈ [0, 1] - рассматриваемый отрезок (лежащий внутри U), то можно применить описанную выше процедуру параметризации к каждой из составляющих функций ж_я (я = 1, ..., м) из ж (в обозначениях выше установите у = Икс + час). Поступая так, можно найти точки Икс + т_ячас на отрезке, удовлетворяющем

${displaystyle f_ {i} (x + h) -f_ {i} (x) = abla f_ {i} (x + t_ {i} h) cdot h.}$

Но вообще не будет Один точка Икс + т * ч на отрезке, удовлетворяющем

${displaystyle f_ {i} (x + h) -f_ {i} (x) = abla f_ {i} (x + t ^ {*} h) cdot h.}$

для всех я одновременно. Например, определите:

${displaystyle {egin {case} f: [0,2pi] o mathbf {R} ^ {2} f (x) = (cos (x), sin (x)) end {case}}}$

потом ${displaystyle f (2pi) -f (0) = mathbf {0} в mathbf {R} ^ {2}}$, но ${displaystyle f_ {1} '(x) = - sin (x)}$ и ${displaystyle f_ {2} '(x) = cos (x)}$ никогда одновременно не равны нулю, поскольку ${displaystyle x}$ колеблется над ${displaystyle left [0,2pi ight]}$.

Однако некоторый тип обобщения теоремы о среднем на вектор-функции получается следующим образом: Пусть ж - непрерывно дифференцируемая вещественнозначная функция, заданная на открытом интервале я, и разреши Икс а также Икс + час быть точками я. Теорема о среднем значении одной переменной говорит нам, что существуют некоторые т * между 0 и 1 такие, что

${displaystyle f (x + h) -f (x) = f '(x + t ^ {*} h) cdot h.}$

С другой стороны, мы имеем основная теорема исчисления с последующей заменой переменных,

${displaystyle f (x + h) -f (x) = int _ {x} ^ {x + h} f '(u), du = left (int _ {0} ^ {1} f' (x + th ), dtight) cdot h.}$

Таким образом, значение f ′(Икс + т * ч) в конкретной точке т * заменено средним значением

${displaystyle int _ {0} ^ {1} f '(x + th), dt.}$

Эту последнюю версию можно обобщить на векторные функции:

Лемма 1. Позволять U ⊂ р^п быть открытым, ж : U → р^м непрерывно дифференцируемый, и Икс ∈ U, час ∈ р^п векторы такие, что отрезок прямой Икс + th, 0 ≤ т ≤ 1 остается в U. Тогда у нас есть:

${displaystyle f (x + h) -f (x) = left (int _ {0} ^ {1} Df (x + th), dtight) cdot h,}$

куда Df обозначает Матрица якобиана из ж а интеграл матрицы следует понимать покомпонентно.

Доказательство. Позволять ж₁, ..., ж_м обозначим компоненты ж и определите:

${displaystyle {egin {case} g_ {i}: [0,1] o mathbf {R} g_ {i} (t) = f_ {i} (x + th) end {case}}}$

Тогда у нас есть

${displaystyle {egin {align} & f_ {i} (x + h) -f_ {i} (x) = g_ {i} (1) -g_ {i} (0) = int _ {0} ^ {1} g_ {i} '(t), dt = {} & int _ {0} ^ {1} left (sum _ {j = 1} ^ {n} {frac {partial f_ {i}} {partial x_ {j }}} (x + th) h_ {j} ight), dt = sum _ {j = 1} ^ {n} left (int _ {0} ^ {1} {frac {partial f_ {i}} {partial x_ {j}}} (x + th), dtight) h_ {j} .end {выровнено}}}$

Утверждение следует из того, что Df - матрица, состоящая из компонентов ${displaystyle {frac {partial f_ {i}} {partial x_ {j}}}.}$

Лемма 2. Позволять v : [а, б] → р^м - непрерывная функция, определенная на интервале [а, б] ⊂ р. Тогда у нас есть

${displaystyle left | int _ {a} ^ {b} v (t), dtight | leqslant int _ {a} ^ {b} | v (t) |, dt.}$

Доказательство. Позволять ты в р^м обозначим значение интеграла

${displaystyle u: = int _ {a} ^ {b} v (t), dt.}$

Теперь у нас есть (используя Неравенство Коши – Шварца ):

${displaystyle | u | ^ {2} = langle u, uangle = leftlangle int _ {a} ^ {b} v (t), dt, uightangle = int _ {a} ^ {b} langle v (t), uangle , dtleqslant int _ {a} ^ {b} | v (t) | cdot | u |, dt = | u | int _ {a} ^ {b} | v (t) |, dt}$

Теперь отменяя норму ты с обоих концов дает нам желаемое неравенство.

Неравенство средних значений. Если норма Df(Икс + th) ограничена некоторой постоянной M за т в [0, 1], то

${displaystyle | f (x + h) -f (x) | leqslant M | h |.}$

Доказательство. Из леммы 1 и 2 следует, что

${displaystyle | f (x + h) -f (x) | = left | int _ {0} ^ {1} (Df (x + th) cdot h), dtight | leqslant int _ {0} ^ {1} | Df (x + th) | cdot | h |, dtleqslant M | h |.}$

Теоремы о среднем значении для определенных интегралов

Первая теорема о среднем значении для определенных интегралов

Геометрически: интерпретация f (c) как высота прямоугольника и б–а что касается ширины, этот прямоугольник имеет такую ​​же площадь, что и область под кривой из а к б^[7]

Позволять ж : [а, б] → р - непрерывная функция. Тогда существует c в [а, б] такой, что

${displaystyle int _ {a} ^ {b} f (x), dx = f (c) (b-a).}$

Поскольку среднее значение ж на [а, б] определяется как

${displaystyle {frac {1} {b-a}} int _ {a} ^ {b} f (x), dx,}$

мы можем интерпретировать вывод как ж достигает своего среднего значения в некоторых c в (а, б).^[8]

В общем, если ж : [а, б] → р непрерывно и грамм - интегрируемая функция, не меняющая знака на [а, б], то существует c в (а, б) такие, что

${displaystyle int _ {a} ^ {b} f (x) g (x), dx = f (c) int _ {a} ^ {b} g (x), dx.}$

Доказательство первой теоремы о среднем для определенных интегралов

Предполагать ж : [а, б] → р непрерывно и грамм - неотрицательная интегрируемая функция на [а, б]. Посредством теорема об экстремальном значении, Существует м и M так что для каждого Икс в [а, б], ${displaystyle mleqslant f (x) leqslant M}$ и ${displaystyle f [a, b] = [m, M]}$. С грамм неотрицательно,

${displaystyle mint _ {a} ^ {b} g (x), dxleqslant int _ {a} ^ {b} f (x) g (x), dxleqslant Mint _ {a} ^ {b} g (x), dx.}$

Теперь позвольте

${displaystyle I = int _ {a} ^ {b} g (x), dx.}$

Если ${displaystyle I = 0}$, мы закончили с

${displaystyle 0leqslant int _ {a} ^ {b} f (x) g (x), dxleqslant 0}$

средства

${displaystyle int _ {a} ^ {b} f (x) g (x), dx = 0,}$

так что для любого c в (а, б),

${displaystyle int _ {a} ^ {b} f (x) g (x), dx = f (c) I = 0.}$

Если я ≠ 0, то

${displaystyle mleqslant {frac {1} {I}} int _ {a} ^ {b} f (x) g (x), dxleqslant M.}$

Посредством теорема о промежуточном значении, ж достигает каждого значения интервала [м, M], поэтому для некоторых c в [а, б]

${displaystyle f (c) = {frac {1} {I}} int _ {a} ^ {b} f (x) g (x), dx,}$

то есть,

${displaystyle int _ {a} ^ {b} f (x) g (x), dx = f (c) int _ {a} ^ {b} g (x), dx.}$

Наконец, если грамм отрицательный на [а, б], тогда

${displaystyle Mint _ {a} ^ {b} g (x), dxleqslant int _ {a} ^ {b} f (x) g (x), dxleqslant mint _ {a} ^ {b} g (x), dx,}$

и мы по-прежнему получаем тот же результат, что и выше.

QED

Вторая теорема о среднем значении для определенных интегралов

Существуют несколько различных теорем, называемых Вторая теорема о среднем значении для определенных интегралов. Обычно встречается следующая версия:

Если грамм : [а, б] → р положительный монотонно убывающий функция и φ: [а, б] → р - интегрируемая функция, то существует число Икс в (а, б] такой, что

${displaystyle int _ {a} ^ {b} G (t) varphi (t), dt = G (a ^ {+}) int _ {a} ^ {x} varphi (t), dt.}$

Здесь ${displaystyle G (a ^ {+})}$ означает ${displaystyle {lim _ {x o a ^ {+}} G (x)}}$, существование которых следует из условий. Отметим, что очень важно, чтобы интервал (а, б] содержит б. Вариант, не имеющий этого требования:^[9]

Если грамм : [а, б] → р это монотонный (не обязательно убывающая и положительная) функция и φ: [а, б] → р - интегрируемая функция, то существует число Икс в (а, б) такие, что

${displaystyle int _ {a} ^ {b} G (t) varphi (t), dt = G (a ^ {+}) int _ {a} ^ {x} varphi (t), dt + G (b ^ {-}) int _ {x} ^ {b} varphi (t), dt.}$

Теорема о среднем значении для интегрирования не работает для векторных функций

Если функция ${displaystyle G}$ возвращает многомерный вектор, тогда MVT для интегрирования не верен, даже если домен ${displaystyle G}$ также многомерна.

Например, рассмотрим следующую двумерную функцию, определенную на ${displaystyle n}$-мерный куб:

${displaystyle {egin {case} G: [0,2pi] ^ {n} o mathbb {R} ^ {2} G (x_ {1}, cdots, x_ {n}) = left (sin (x_ {1 } + cdots + x_ {n}), cos (x_ {1} + cdots + x_ {n}) ight) end {case}}}$

Тогда по симметрии легко увидеть, что среднее значение ${displaystyle G}$ по его области (0,0):

${displaystyle int _ {[0,2pi] ^ {n}} G (x_ {1}, cdots, x_ {n}) dx_ {1} cdots dx_ {n} = (0,0)}$

Однако нет смысла ${displaystyle G = (0,0)}$, потому что ${displaystyle | G | = 1}$ повсюду.

Вероятностный аналог теоремы о среднем значении

Позволять Икс и Y быть неотрицательным случайные переменные такое, что E [Икс] Y] <∞ и ${displaystyle Xleqslant _ {st} Y}$ (т.е. Икс меньше чем Y в обычный стохастический порядок ). Тогда существует абсолютно непрерывная неотрицательная случайная величина Z имея функция плотности вероятности

${displaystyle f_ {Z} (x) = {Pr (Y> x) -Pr (X> x) over {m {E}} [Y] - {m {E}} [X]} ,, qquad xgeqslant 0 .}$

Позволять грамм быть измеримый и дифференцируемая функция такое, что E [грамм(Икс)], E [грамм(Y)] <∞, и пусть ее производная грамм' быть измеримыми и Интегрируемый по Риману на интервале [Икс, у] для всех у ≥ Икс ≥ 0. Тогда E [грамм'(Z)] конечно и^[10]

${displaystyle {m {E}} [g (Y)] - {m {E}} [g (X)] = {m {E}} [g '(Z)], [{m {E}} ( Y) - {m {E}} (X)].}$

Обобщение в комплексном анализе

Как отмечалось выше, теорема не выполняется для дифференцируемых комплекснозначных функций. Вместо этого формулируется такое обобщение теоремы:^[11]

Позволять ж : Ω → C быть голоморфная функция на открытом выпуклом множестве Ω, и пусть а и б - различные точки в Ω. Тогда существуют точки ты, v на L_ab (отрезок от а к б) такие, что

${displaystyle mathrm {Re} (f '(u)) = mathrm {Re} left ({frac {f (b) -f (a)} {b-a}} ight),}$

${displaystyle mathrm {Im} (f '(v)) = mathrm {Im} left ({frac {f (b) -f (a)} {b-a}} ight).}$

Где Re () - действительная часть, а Im () - мнимая часть комплексной функции.

Смотрите также

• Метод Newmark-beta
• Теорема о среднем значении (разделенные разности)
• Принцип ипподрома
• Столярского

Примечания

внешняя ссылка

• «Теорема Коши», Энциклопедия математики, EMS Press, 2001 [1994]
• PlanetMath: Теорема о среднем значении
• Вайсштейн, Эрик В. «Теорема о среднем значении». MathWorld.
• Вайсштейн, Эрик В. "Теорема Коши о среднем значении". MathWorld.
• «Теорема о среднем значении: интуиция, лежащая в основе теоремы о среднем значении» на Ханская академия