Адвекция - Advection

В области физика, инженерное дело, и науки о Земле, адвекция это транспорт вещества или количества путем объемного движения. Свойства этого вещества передаются ему. Обычно большая часть адвегированного вещества представляет собой жидкость. Адвективное вещество обладает следующими свойствами: консервированный свойства, такие как энергия. Примером адвекции является перенос загрязняющие вещества или ил в река объемным потоком воды ниже по потоку. Еще одна распространенная величина - энергия или энтальпия. Здесь текучая среда может быть любым материалом, содержащим тепловую энергию, например воды или воздуха. В общем, любое вещество или консервированное, обширный количество может быть добавлено жидкость которые могут содержать или содержать количество или вещество.

Во время адвекции жидкость переносит некоторое сохраненное количество или материал посредством объемного движения. Движение жидкости описывается математически как векторное поле, а транспортируемый материал описывается скалярное поле показывая его распространение в пространстве. Для адвекции необходимы токи в жидкости, и поэтому она не может происходить в твердых телах. Не включает транспортировку веществ молекулярная диффузия.

Адвекцию иногда путают с более всеобъемлющим процессом конвекция который представляет собой комбинацию адвективного транспорта и диффузионного транспорта.

В метеорология и физическая океанография, адвекция часто относится к переносу какого-либо свойства атмосферы или океан, такие как высокая температура, влажность (см. влажность ) или соленость. Адвекция важна для образования орографический облака и осадки воды из облаков, как часть гидрологический цикл.

Различие между адвекцией и конвекцией

Период, термин адвекция часто служит синонимом конвекция, и это соответствие терминов используется в литературе. С технической точки зрения, конвекция применяется к движению жидкости (часто из-за градиентов плотности, создаваемых тепловыми градиентами), тогда как адвекция - это движение некоторого материала за счет скорости жидкости. Таким образом, что несколько сбивает с толку, технически правильно думать об импульсе, переносимом полем скорости в уравнениях Навье-Стокса, хотя результирующее движение можно было бы рассматривать как конвекцию. Из-за особого использования термина конвекция для обозначения переноса в сочетании с температурными градиентами, вероятно, безопаснее использовать термин адвекция, если кто-то не уверен в том, какая терминология лучше всего описывает их конкретную систему.

Метеорология

В метеорология и физическая океанография, адвекция часто относится к горизонтальному переносу какого-либо свойства атмосферы или океан, такие как высокая температура, влажность или соленость, а конвекция обычно относится к вертикальному переносу (вертикальная адвекция). Адвекция важна для образования орографические облака (вынужденная конвекция местности) и выпадение воды из облаков, как часть гидрологический цикл.

Другие количества

Уравнение переноса также применимо, если переносимая величина представлена функция плотности вероятности в каждой точке, хотя учесть диффузию сложнее.^{[нужна цитата ]}

Математика адвекции

В уравнение переноса это уравнение в частных производных который управляет движением сохраненного скалярное поле как это принято известными векторное поле скорости. Он выводится с использованием скалярного поля закон сохранения, вместе с Теорема Гаусса, и принимая бесконечно малый предел.

Одним из легко визуализируемых примеров адвекции является перенос чернил, сброшенных в реку. По мере того, как река течет, чернила будут двигаться вниз по течению "пульсирующе" за счет адвекции, поскольку движение воды переносит чернила. Если добавить в озеро без значительного объемного потока воды, чернила просто разойдутся наружу от источника в диффузный способ, который не является адвекцией. Обратите внимание, что по мере движения вниз по потоку «импульс» чернил также распространяется посредством диффузии. Сумма этих процессов называется конвекция.

Уравнение переноса

В декартовых координатах адвекция оператор является

{ displaystyle mathbf {u} cdot nabla = u_ {x} { frac { partial} { partial x}} + u_ {y} { frac { partial} { partial y}} + u_ {z} { frac { partial} { partial z}}}

.

где ${ displaystyle mathbf {u} = (u_ {x}, u_ {y}, u_ {z})}$ это поле скорости, и ${ displaystyle nabla}$ это дель оператор (обратите внимание, что Декартовы координаты используются здесь).

Уравнение переноса для сохраняющейся величины, описываемое скалярное поле ${ displaystyle psi}$ математически выражается уравнение неразрывности:

${ displaystyle { frac { partial psi} { partial t}} + набла cdot left ( psi { mathbf {u}} right) = 0}$

где ${ Displaystyle набла cdot}$ это расхождение оператор и снова ${ displaystyle mathbf {u}}$ это векторное поле скорости. Часто предполагается, что поток несжимаемый, это поле скорости удовлетворяет

{ Displaystyle набла cdot { mathbf {u}} = 0}

.

В таком случае, ${ displaystyle mathbf {u}}$ как говорят соленоидный. Если это так, то приведенное выше уравнение можно переписать как

${ displaystyle { frac { partial psi} { partial t}} + { mathbf {u}} cdot nabla psi = 0}$

В частности, если течение стационарное, то

{ Displaystyle { mathbf {u}} cdot nabla psi = 0}

что показывает, что ${ displaystyle psi}$ постоянна вдоль рационализировать. Следовательно, ${ Displaystyle partial psi / partial t = 0,}$ так ${ displaystyle psi}$ не меняется во времени.

Если векторная величина ${ Displaystyle mathbf {а}}$ (например, магнитное поле ) продвигается соленоидный поле скорости ${ displaystyle mathbf {u}}$ , приведенное выше уравнение переноса принимает следующий вид:

{ displaystyle { frac { partial { mathbf {a}}} { partial t}} + left ({ mathbf {u}} cdot nabla right) { mathbf {a}} = 0 .}

Вот, ${ Displaystyle mathbf {а}}$ это векторное поле вместо скалярное поле ${ displaystyle psi}$ .

Решение уравнения

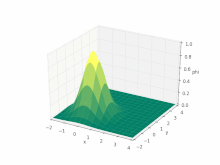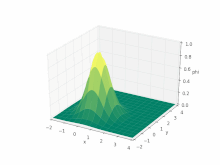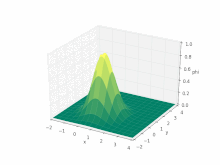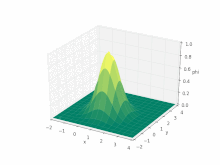
Моделирование уравнения переноса, где ты = (грех т, cos т) соленоидально.

Уравнение переноса решить непросто численно: система - это гиперболическое уравнение в частных производных, и интерес обычно сосредоточен на прерывистый «шоковые» решения (с которыми, как известно, сложно работать с численными схемами).

Даже с одним пространственным измерением и постоянным поле скорости, система остается сложной для моделирования. Уравнение становится

{ displaystyle { frac { partial psi} { partial t}} + u_ {x} { frac { partial psi} { partial x}} = 0}

где ${ Displaystyle psi = psi (х, t)}$ это скалярное поле адвекция и ${ displaystyle u_ {x}}$ это ${ displaystyle x}$ компонент вектора ${ displaystyle mathbf {u} = (u_ {x}, 0,0)}$ .

Обработка оператора адвекции в уравнениях Навье-Стокса несжимаемой жидкости

По словам Занга,^[1] численному моделированию может помочь рассмотрение кососимметричный форма для оператора переноса.

{ displaystyle { frac {1} {2}} { mathbf {u}} cdot nabla { mathbf {u}} + { frac {1} {2}} nabla ({ mathbf {u }} { mathbf {u}})}

где

{ displaystyle nabla ({ mathbf {u}} { mathbf {u}}) = [ nabla ({ mathbf {u}} u_ {x}), nabla ({ mathbf {u}} u_ {y}), nabla ({ mathbf {u}} u_ {z})]}

и ${ displaystyle mathbf {u}}$ то же, что и выше.

Поскольку косая симметрия подразумевает только воображаемый собственные значения, эта форма уменьшает "взрыв" и "спектральную блокировку", которые часто возникают в численных решениях с резкими разрывами (см. Boyd^[2]).

С помощью тождества с векторным исчислением, эти операторы также могут быть выражены другими способами, доступными в большем количестве программных пакетов для большего количества систем координат.

{ displaystyle mathbf {u} cdot nabla mathbf {u} = nabla left ({ frac { | mathbf {u} | ^ {2}} {2}} right) + слева ( nabla times mathbf {u} right) times mathbf {u}}

{ displaystyle { frac {1} {2}} mathbf {u} cdot nabla mathbf {u} + { frac {1} {2}} nabla ( mathbf {u} mathbf {u }) = nabla left ({ frac { | mathbf {u} | ^ {2}} {2}} right) + left ( nabla times mathbf {u} right) раз mathbf {u} + { frac {1} {2}} mathbf {u} ( nabla cdot mathbf {u})}

Эта форма также показывает, что кососимметричный оператор вносит ошибку при расхождении поля скорости. Решение уравнения переноса численными методами является очень сложной задачей, и по этому поводу имеется обширная научная литература.

Смотрите также

использованная литература

^ Занг, Томас (1991). «О вращении и кососимметричных формах для моделирования течения несжимаемой жидкости». Прикладная вычислительная математика. 7: 27–40. Bibcode:1991АпНМ .... 7 ... 27Z. Дои:10.1016/0168-9274(91)90102-6.
^ Бойд, Джон П. (2000). Спектральные методы Чебышева и Фурье 2-е издание. Дувр. п. 213.

[1] Занг, Томас (1991). «О вращении и кососимметричных формах для моделирования течения несжимаемой жидкости». Прикладная вычислительная математика. 7: 27–40. Bibcode:1991АпНМ .... 7 ... 27Z. Дои:10.1016/0168-9274(91)90102-6.

[2] Бойд, Джон П. (2000). Спектральные методы Чебышева и Фурье 2-е издание. Дувр. п. 213.

[1]

[2]

Метеорологические данные и переменные
Общее	Адиабатические процессы Адвекция Плавучесть Промежуток времени Молнии Поверхностное солнечное излучение Анализ погоды на поверхности Видимость Завихренность ветер Сдвиг ветра
Конденсация	Облако Облачные ядра конденсации (CCN) Туман Уровень конвективной конденсации (CCL) Повышенный уровень конденсации (LCL) Атмосферные осадки Водяной пар
Конвекция	Конвективная доступная потенциальная энергия (CAPE) Конвективное торможение (CIN) Конвективная нестабильность Конвективный импульсный перенос Условная симметричная неустойчивость Конвективная температура (Т_c) Уровень равновесия (EL) Свободный конвективный слой (FCL) Спиральность K Индекс Уровень свободной конвекции (LFC) Поднятый индекс (LI) Максимальный уровень посылки (MPL) Массовое число Ричардсона (BRN)
Температура	Точка росы (Т_d) Депрессия точки росы Температура по сухому термометру Эквивалентная температура (Т_е) Индекс погоды лесных пожаров Индекс Хейнса Индекс тепла Humidex Влажность Относительная влажность (RH) Соотношение смешивания Возможная температура (θ) Эквивалентная потенциальная температура (θ_е) Температура поверхности моря (SST) Термодинамическая температура Давление газа Виртуальная температура Температура влажного термометра Температура по влажному термометру Потенциальная температура влажного термометра Холодный ветер
Давление	Атмосферное давление Бароклинность Баротропность Градиент давления Сила градиента давления (PGF)