Дисперсия (оптика) - Dispersion (optics)

В оптика, разброс это явление, в котором фазовая скорость волны зависит от ее частоты.[1]Средства массовой информации, обладающие этим общим свойством, можно назвать дисперсионные среды. Иногда термин хроматический разброс используется для специфичности. Хотя этот термин используется в области оптики для описания свет и другие электромагнитные волны, дисперсия в том же смысле может применяться к любому виду волнового движения, например акустическая дисперсия в случае звуковых и сейсмических волн, в гравитационные волны (океанские волны) и для телекоммуникационных сигналов вдоль линии передачи (такие как коаксиальный кабель ) или оптоволокно.
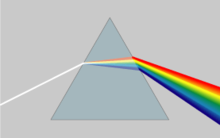
В оптике одним из важных и известных последствий дисперсии является изменение угла преломление разных цветов света,[2] как видно из спектра, создаваемого дисперсионным призма И в Хроматическая аберрация линз. Дизайн комплекса ахроматические линзы, при котором хроматическая аберрация в значительной степени устраняется, использует количественную оценку дисперсии стекла, задаваемую его Число Аббе V, где ниже Числа Аббе соответствуют больше разброс по видимый спектр. В некоторых приложениях, таких как телекоммуникации, часто не важна абсолютная фаза волны, а важна только ее распространение. волновые пакеты или «импульсы»; в этом случае нас интересуют только вариации групповая скорость с частотой, так называемые дисперсия групповой скорости.
Примеры
Самый известный пример дисперсии, вероятно, радуга, в котором дисперсия вызывает пространственное разделение белого свет на составляющие различных длины волн (разные цвета ). Однако дисперсия влияет и на многие другие обстоятельства: например, дисперсия групповой скорости (GVD) причины импульсы распространяться в оптические волокна, ухудшающие сигналы на больших расстояниях; кроме того, сокращение между дисперсией групповой скорости и нелинейный эффекты приводит к солитон волны.
Материальная и волноводная дисперсия
Чаще всего хроматическая дисперсия относится к дисперсии объемного материала, то есть изменению показатель преломления с оптической частотой. Однако в волновод есть также феномен волноводная дисперсия, и в этом случае фазовая скорость волны в конструкции зависит от ее частоты просто из-за геометрии конструкции. В более общем смысле «волноводная» дисперсия может возникать для волн, распространяющихся через любую неоднородную структуру (например, фотонный кристалл ) независимо от того, приурочены ли волны к какой-либо области.[сомнительный ] В волноводе и то и другое типы дисперсии обычно присутствуют, хотя они не являются строго аддитивными.[нужна цитата ] Например, в волоконной оптике дисперсия материала и волновода может эффективно компенсировать друг друга, создавая длина волны с нулевой дисперсией, важно для быстрого волоконно-оптическая связь.
Дисперсия материала в оптике

Дисперсия материала может быть желательным или нежелательным эффектом в оптических приложениях. Рассеивание света стеклянными призмами используется для построения спектрометры и спектрорадиометры. Голографический решетки также используются, поскольку они позволяют более точно различать длины волн. Однако в линзах дисперсия вызывает Хроматическая аберрация, нежелательный эффект, который может ухудшить качество изображения в микроскопах, телескопах и фотографических объективах.
В фазовая скорость, vволны в данной однородной среде определяется выражением
где c это скорость света в вакууме и п это показатель преломления среды.
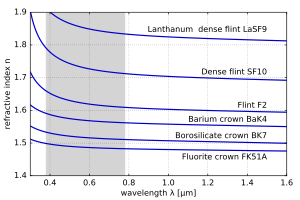
Как правило, показатель преломления зависит от частоты. ж света, таким образом п = п(ж) или, альтернативно, по длине волны п = п(λ). Зависимость показателя преломления материала от длины волны обычно количественно определяется его Число Аббе или его коэффициенты в эмпирической формуле, такой как Коши или Уравнения Селлмейера.
Из-за Отношения Крамерса – Кронига, зависимость действительной части показателя преломления от длины волны связана с материалом поглощение, описываемый мнимой частью показателя преломления (также называемой коэффициент экстинкции ). В частности, для немагнитных материалов (μ = μ0 ), восприимчивость χ в соотношениях Крамерса – Кронига электрическая восприимчивость χе = п2 − 1.
Наиболее часто наблюдаемым следствием дисперсии в оптике является разделение белый свет в цветовой спектр по призма. Из Закон Снеллиуса видно, что угол преломление Количество света в призме зависит от показателя преломления материала призмы. Поскольку этот показатель преломления зависит от длины волны, отсюда следует, что угол, под которым преломляется свет, также будет изменяться с длиной волны, вызывая угловое разделение цветов, известное как угловая дисперсия.
Для видимого света показатели преломления п большинства прозрачных материалов (например, воздуха, стекла) уменьшаются с увеличением длины волны λ:
или альтернативно:
В этом случае говорят, что среда имеет нормальная дисперсия. Принимая во внимание, что если индекс увеличивается с увеличением длины волны (что обычно имеет место в ультрафиолетовом[4]) среда называется имеющей аномальная дисперсия.
На границе такого материала с воздухом или вакуумом (индекс ~ 1) закон Снеллиуса предсказывает, что свет падает под углом θ к нормальный будет преломляться под углом arcsin (грех θ/п). Таким образом, синий свет с более высоким показателем преломления будет изгибаться сильнее, чем красный свет, что приводит к хорошо известному радуга шаблон.
Дисперсия групповой скорости

Помимо простого описания изменения фазовой скорости по длине волны, более серьезное последствие дисперсии во многих приложениях называется дисперсия групповой скорости. Пока фазовая скорость v определяется как v = c/п, это описывает только одну частотную составляющую. Когда разные частотные составляющие комбинируются вместе, как, например, при рассмотрении сигнала или импульса, часто больше интересует групповая скорость который описывает скорость, с которой распространяется импульс или информация, наложенная на волну (модуляция). В сопровождающей анимации видно, что сама волна (оранжево-коричневая) движется с фазовой скоростью, которая намного превышает скорость волны. конверт (черный), что соответствует групповой скорости. Этот импульс может быть, например, сигналом связи, и его информация распространяется только с групповой скоростью, даже если он состоит из волновых фронтов, продвигающихся с большей скоростью (фазовая скорость).
Групповую скорость можно вычислить по кривой показателя преломления. п (ω) или более прямо из волнового числа к = ωn / c где ω это радианная частота ω = 2πf. В то время как одно выражение для фазовой скорости имеет вид vп= ω / k, групповая скорость может быть выражена через производная: vг=dω / dk. Или по фазовой скорости vп,
Когда присутствует дисперсия, групповая скорость не только не будет равна фазовой скорости, но, как правило, сама будет изменяться в зависимости от длины волны. Это известно как дисперсия групповой скорости (ДГС) и вызывает уширение короткого светового импульса, поскольку различные частотные компоненты в пределах импульса перемещаются с разной скоростью. Дисперсия групповой скорости количественно определяется как производная от взаимный групповой скорости относительно радианной частоты, что приводит к дисперсия групповой скорости=d2k / dω2.
Если световой импульс распространяется через материал с положительной дисперсией групповой скорости, то компоненты с более короткой длиной волны распространяются медленнее, чем компоненты с большей длиной волны. Таким образом, пульс становится положительно щебетал, или щебечет, частота которых увеличивается со временем. С другой стороны, если импульс проходит через материал с отрицательной дисперсией групповой скорости, более коротковолновые компоненты перемещаются быстрее, чем более длинные, и импульс становится отрицательно щебетал, или чириканье, частота которых уменьшается со временем.
В параметр дисперсии групповой скорости:
часто используется для количественной оценки GVD, которая пропорциональна D через отрицательный фактор:
По мнению некоторых авторов, среда имеет нормальная дисперсия/аномальная дисперсия для определенной длины волны вакуума λ0 если второй производная показателя преломления, рассчитанного в λ0 положительно / отрицательно или, что то же самое, если D(λ0) отрицательный / положительный.[5] Это определение касается дисперсии групповой скорости, и его не следует путать с определением, данным в предыдущем разделе. Эти два определения в целом не совпадают, поэтому читатель должен понимать контекст.
Контроль рассеивания
Результатом ДГС, будь то положительный или отрицательный, в конечном итоге является расширение импульса во времени. Это делает управление дисперсией чрезвычайно важным в системах оптической связи на основе оптического волокна, поскольку, если дисперсия слишком высока, группа импульсов, представляющая поток битов, будет распространяться во времени и сливаться, делая поток битов неразборчивым. Это ограничивает длину волокна, по которому сигнал может быть отправлен без регенерации. Одним из возможных ответов на эту проблему является отправка сигналов по оптическому волокну на длине волны, при которой ДГС равна нулю (например, около 1,3–1,5 мкм в кремнезем волокна ), поэтому для импульсов на этой длине волны дисперсия минимальна. Однако на практике этот подход вызывает больше проблем, чем решает, поскольку нулевая ДГС неприемлемо усиливает другие нелинейные эффекты (такие как четырехволновое смешение ). Другой возможный вариант - использовать солитон импульсы в режиме отрицательной дисперсии, форма оптического импульса, в которой используется нелинейно-оптический эффект для самостоятельного поддержания формы. Однако у солитонов есть практическая проблема, заключающаяся в том, что они требуют, чтобы в импульсе поддерживался определенный уровень мощности, чтобы нелинейный эффект имел правильную силу. Вместо этого решение, которое в настоящее время используется на практике, состоит в том, чтобы выполнить компенсацию дисперсии, обычно путем согласования волокна с другим волокном с дисперсией противоположного знака, чтобы компенсировать эффекты дисперсии; такая компенсация в конечном итоге ограничивается нелинейными эффектами, такими как фазовая самомодуляция, которые взаимодействуют с дисперсией, что затрудняет отмену.
Контроль дисперсии также важен в лазеры которые производят короткие импульсы. Общая дисперсия оптический резонатор является основным фактором при определении длительности импульсов, излучаемых лазером. Пара призмы могут быть устроены для получения чистой отрицательной дисперсии, которая может использоваться для уравновешивания обычно положительной дисперсии лазерной среды. Дифракционные решетки также может использоваться для создания дисперсионных эффектов; они часто используются в системах мощных лазерных усилителей. Недавно была разработана альтернатива призм и решеткам: щебечутые зеркала. Эти диэлектрические зеркала имеют покрытие, так что разные длины волн имеют разную длину проникновения и, следовательно, разные групповые задержки. Слои покрытия могут быть адаптированы для достижения чистой отрицательной дисперсии.
В волноводах
Волноводы обладают высокой дисперсией из-за своей геометрии (а не только из-за состава материала). Оптические волокна представляют собой своего рода волновод для оптических частот (света), широко используемых в современных телекоммуникационных системах. Скорость, с которой данные могут передаваться по одному волокну, ограничена расширением импульса из-за хроматической дисперсии среди других явлений.
В общем случае для волноводной моды с угловая частота ω(β) на постоянная распространения β (так что электромагнитные поля в направлении распространения z колебаться пропорционально ея(βz−ωt)) групповая скорость параметр дисперсии D определяется как:[6]
где λ = 2πc/ω - длина волны вакуума и vг = dω/dβ - групповая скорость. Эта формула обобщает формулу из предыдущего раздела для однородных сред и включает как дисперсию волновода, так и дисперсию материала. Причина такого определения дисперсии заключается в том, что |D| - (асимптотическое) временное расширение импульса Δт на единицу ширины полосыλ на единицу пройденного расстояния, обычно указывается в пс /нм /км для оптических волокон.
На случай, если многомодовые оптические волокна, так называемые модальная дисперсия также приведет к уширению импульса. Даже в одномодовые волокна, уширение импульса может происходить в результате поляризационная модовая дисперсия (так как есть еще два режима поляризации). Эти нет примеры хроматической дисперсии, поскольку они не зависят от длины волны или пропускная способность импульсов.
Дисперсия высшего порядка в широкой полосе пропускания
Когда в одном волновом пакете присутствует широкий диапазон частот (широкая полоса пропускания), например, в ультракороткий импульс или щебетал пульс или другие формы расширенный спектр передачи, может быть неточным аппроксимировать дисперсию константой по всей полосе пропускания, и требуются более сложные вычисления для вычисления таких эффектов, как расширение импульса.
В частности, параметр дисперсии D определенное выше получается только из одной производной групповой скорости. Высшие производные известны как дисперсия высшего порядка.[7] Эти термины просто Серия Тейлор расширение соотношение дисперсии β(ω) среды или волновода вокруг некоторой конкретной частоты. Их влияние можно рассчитать путем численной оценки Преобразования Фурье осциллограммы, через интеграцию высших порядков медленно меняющиеся приближения огибающей, автор двухступенчатый метод (который может использовать точное дисперсионное соотношение, а не ряд Тейлора), или путем прямого моделирования полного Уравнения Максвелла а не приближенное уравнение огибающей.
Пространственная дисперсия
В электромагнетизме и оптике термин разброс обычно относится к вышеупомянутой временной или частотной дисперсии. Пространственная дисперсия относится к нелокальному отклику среды на пространство; это можно переформулировать как зависимость диэлектрической проницаемости от волнового вектора. Для образцового анизотропный среда, пространственное соотношение между электрический и электрическое поле смещения можно выразить как свертка:[8]
где ядро диэлектрический отклик (восприимчивость); его индексы делают его в целом тензор для учета анизотропии среды. Пространственная дисперсия ничтожна в большинстве макроскопических случаев, когда масштаб изменения намного больше размеров атома, потому что диэлектрическое ядро вымирает на макроскопических расстояниях. Тем не менее, это может привести к заметным макроскопическим эффектам, особенно в проводящих средах, таких как металлы, электролиты и плазма. Пространственная дисперсия также играет роль в оптическая активность и Доплеровское уширение,[8] а также в теории метаматериалы.[9]
В геммологии
| имя | B – G | C – F |
|---|---|---|
| Киноварь (HgS) | 0.40 | — |
| Synth. рутил | 0.330 | 0.190 |
| Рутил (TiO2) | 0.280 | 0.120–0.180 |
| Анатас (TiO2) | 0.213–0.259 | — |
| Вульфенит | 0.203 | 0.133 |
| Ванадинит | 0.202 | — |
| Fabulite | 0.190 | 0.109 |
| Сфалерит (ZnS) | 0.156 | 0.088 |
| Сера (S) | 0.155 | — |
| Стибиотанталит | 0.146 | — |
| Гетит (FeO (OH)) | 0.14 | — |
| Brookite (TiO2) | 0.131 | 0.12–1.80 |
| Цинкит (ZnO) | 0.127 | — |
| Линобат | 0.13 | 0.075 |
| Синтетический муассанит (SiC) | 0.104 | — |
| Касситерит (SnO2) | 0.071 | 0.035 |
| Цирконий (ZrO2) | 0.060 | 0.035 |
| Powellite (CaMoO4) | 0.058 | — |
| Андрадит | 0.057 | — |
| Демантоид | 0.057 | 0.034 |
| Церуссит | 0.055 | 0.033–0.050 |
| Титанит | 0.051 | 0.019–0.038 |
| Бенитоит | 0.046 | 0.026 |
| Англезит | 0.044 | 0.025 |
| Алмаз (С) | 0.044 | 0.025 |
| Бесцветное стекло | 0.041 | — |
| Гиацинт | 0.039 | — |
| Jargoon | 0.039 | — |
| Starlite | 0.039 | — |
| Циркон (ZrSiO4) | 0.039 | 0.022 |
| GGG | 0.038 | 0.022 |
| Шеелит | 0.038 | 0.026 |
| Диоптаз | 0.036 | 0.021 |
| Whe Vinay wellite | 0.034 | — |
| Алебастр | 0.033 | — |
| Гипс | 0.033 | 0.008 |
| Эпидот | 0.03 | 0.012–0.027 |
| Ахроит | 0.017 | — |
| Кордиерит | 0.017 | 0.009 |
| Данбурит | 0.017 | 0.009 |
| Дравит | 0.017 | — |
| Эльбаите | 0.017 | — |
| Гердерит | 0.017 | 0.008–0.009 |
| Hiddenite | 0.017 | 0.010 |
| Индиколит | 0.017 | — |
| Лиддикоатит | 0.017 | — |
| Кунсайт | 0.017 | 0.010 |
| Рубеллит | 0.017 | 0.008–0.009 |
| Шерл | 0.017 | — |
| Скаполит | 0.017 | — |
| Сподумен | 0.017 | 0.010 |
| Турмалин | 0.017 | 0.009–0.011 |
| Верделит | 0.017 | — |
| Андалузит | 0.016 | 0.009 |
| Барит (BaSO4) | 0.016 | 0.009 |
| Евклаз | 0.016 | 0.009 |
| Александрит | 0.015 | 0.011 |
| Хризоберилл | 0.015 | 0.011 |
| Гамбергит | 0.015 | 0.009–0.010 |
| Фенакит | 0.01 | 0.009 |
| Родохрозит | 0.015 | 0.010–0.020 |
| Силлиманит | 0.015 | 0.009–0.012 |
| Смитсонит | 0.014–0.031 | 0.008–0.017 |
| Амблигонит | 0.014–0.015 | 0.008 |
| Аквамарин | 0.014 | 0.009–0.013 |
| Берил | 0.014 | 0.009–0.013 |
| Бразильянит | 0.014 | 0.008 |
| Селестина | 0.014 | 0.008 |
| Гошенит | 0.014 | — |
| Гелиодор | 0.014 | 0.009–0.013 |
| Морганит | 0.014 | 0.009–0.013 |
| Пироксмангит | 0.015 | — |
| Synth. шеелит | 0.015 | — |
| Доломит | 0.013 | — |
| Магнезит (MgCO3) | 0.012 | — |
| Synth. изумруд | 0.012 | — |
| Synth. александрит | 0.011 | — |
| Synth. сапфир (Al2О3) | 0.011 | — |
| Фосфофиллит | 0.010–0.011 | — |
| Энстатит | 0.010 | — |
| Анортит | 0.009–0.010 | — |
| Актинолит | 0.009 | — |
| Еремеевит | 0.009 | — |
| Нефелин | 0.008–0.009 | — |
| Апофиллит | 0.008 | — |
| Hauyne | 0.008 | — |
| Натролит | 0.008 | — |
| Synth. кварц (SiO2) | 0.008 | — |
| Арагонит | 0.007–0.012 | — |
| Авгелит | 0.007 | — |
| Танзанит | 0.030 | 0.011 |
| Тулит | 0.03 | 0.011 |
| Цоизит | 0.03 | — |
| YAG | 0.028 | 0.015 |
| Альмандин | 0.027 | 0.013–0.016 |
| Гессонит | 0.027 | 0.013–0.015 |
| Спессартин | 0.027 | 0.015 |
| Уваровит | 0.027 | 0.014–0.021 |
| Виллемит | 0.027 | — |
| Pleonaste | 0.026 | — |
| Родолит | 0.026 | — |
| Борацит | 0.024 | 0.012 |
| Криолит | 0.024 | — |
| Ставролит | 0.023 | 0.012–0.013 |
| Пироп | 0.022 | 0.013–0.016 |
| Диаспора | 0.02 | — |
| Гроссуляр | 0.020 | 0.012 |
| Гемиморфит | 0.020 | 0.013 |
| Кианит | 0.020 | 0.011 |
| Перидот | 0.020 | 0.012–0.013 |
| Шпинель | 0.020 | 0.011 |
| Везувианит | 0.019–0.025 | 0.014 |
| Клиноцоизит | 0.019 | 0.011–0.014 |
| Лабрадорит | 0.019 | 0.010 |
| Аксинит | 0.018–0.020 | 0.011 |
| Эканите | 0.018 | 0.012 |
| Корнерупин | 0.018 | 0.010 |
| Корунд (Al2О3) | 0.018 | 0.011 |
| Родизит | 0.018 | — |
| Рубин (Al2О3) | 0.018 | 0.011 |
| Сапфир (Al2О3) | 0.018 | 0.011 |
| Сингалит | 0.018 | 0.010 |
| Содалит | 0.018 | 0.009 |
| Synth. корунд | 0.018 | 0.011 |
| Диопсид | 0.018–0.020 | 0.01 |
| Изумруд | 0.014 | 0.009–0.013 |
| Топаз | 0.014 | 0.008 |
| Аметист (SiO2) | 0.013 | 0.008 |
| Ангидрит | 0.013 | — |
| Апатит | 0.013 | 0.010 |
| Апатит | 0.013 | 0.008 |
| Авантюрин | 0.013 | 0.008 |
| Цитрин | 0.013 | 0.008 |
| Морион | 0.013 | — |
| Празиолит | 0.013 | 0.008 |
| Кварцевый (SiO2) | 0.013 | 0.008 |
| Дымчатый кварц (SiO2) | 0.013 | 0.008 |
| Розовый кварц (SiO2) | 0.013 | 0.008 |
| Альбит | 0.012 | — |
| Bytownite | 0.012 | — |
| Полевой шпат | 0.012 | 0.008 |
| Лунный камень | 0.012 | 0.008 |
| Ортоклаз | 0.012 | 0.008 |
| Поллюцит | 0.012 | 0.007 |
| Санидин | 0.012 | — |
| Солнечный камень | 0.012 | — |
| Бериллонит | 0.010 | 0.007 |
| Канкринит | 0.010 | 0.008–0.009 |
| Лейцит | 0.010 | 0.008 |
| Обсидиан | 0.010 | — |
| Стронцианит | 0.008–0.028 | — |
| Кальцит (CaCO3) | 0.008–0.017 | 0.013–0.014 |
| Флюорит (CaF2) | 0.007 | 0.004 |
| Гематит | 0.500 | — |
| Синтетический касситерит (SnO2) | 0.041 | — |
| Ганите | 0.019–0.021 | — |
| Датолит | 0.016 | — |
| Тремолит | 0.006–0.007 | — |
в техническая терминология из геммология, разброс - разница в показателях преломления материала в точках B и G (686,7нм и 430,8 нм) или C и F (656,3 нм и 486,1 нм) Длины волн фраунгофера, и предназначен для выражения степени, в которой призма срезается с драгоценный камень демонстрирует «огонь». Огонь - это разговорный термин, используемый геммологами для описания дисперсной природы драгоценного камня или ее отсутствия. Дисперсность - это материальное свойство. Количество огня, демонстрируемого данным драгоценным камнем, зависит от углов огранки драгоценного камня, качества полировки, условий освещения, показателя преломления материала, насыщенности цвета и ориентации зрителя относительно драгоценного камня.[10][11]
В изображении
В фотографических и микроскопических объективах дисперсия вызывает Хроматическая аберрация, из-за чего разные цвета в изображении не перекрываются должным образом. Для противодействия этому были разработаны различные методы, такие как использование ахроматы, многоэлементные линзы с очками разной дисперсии. Они построены таким образом, что хроматические аберрации различных частей компенсируются.
Выбросы пульсаров
Было предложено, чтобы этот раздел был Трещина в другую статью под названием Мера дисперсии. (Обсудить) (Ноябрь 2015 г.) |
Пульсары вращающиеся нейтронные звезды, испускающие импульсы с очень регулярными интервалами от миллисекунд до секунд. Астрономы считают, что импульсы излучаются одновременно в широком диапазоне частот. Однако, как наблюдается на Земле, компоненты каждого импульса, излучаемого на более высоких радиочастотах, прибывают раньше, чем те, которые излучаются на более низких частотах. Эта дисперсия происходит из-за ионизированного компонента межзвездная среда, главным образом, свободные электроны, которые делают групповую скорость зависимой от частоты. Дополнительная задержка добавлена с частотой ν является
где дисперсионная постоянная kDM дан кем-то
и мера дисперсии (DM) - столбиковая плотность свободных электронов (полное электронное содержание ) - то есть плотность электронов пе (электронов / см3), проинтегрированная по пути, пройденному фотоном от пульсара до Земли, - и определяется выражением
с единицами парсек на кубический сантиметр (1 шт / см3 = 30.857 × 1021 м−2).[13]
Обычно для астрономических наблюдений эту задержку нельзя измерить напрямую, поскольку время излучения неизвестно. Что может измеряется разница во времени прихода на двух разных частотах. Задержка Δт между высокой частотой νЗдравствуй и низкая частота νвот составляющая пульса будет
Переписывая приведенное выше уравнение через Δт позволяет определять DM путем измерения времени прихода импульсов на нескольких частотах. Это, в свою очередь, может быть использовано для изучения межзвездной среды, а также позволяет комбинировать наблюдения пульсаров на разных частотах.
Смотрите также
- Число Аббе
- Расчет свойств стекла вкл. разброс
- Уравнение Коши
- Отношение дисперсии
- Быстрый всплеск радио (астрономия)
- Теорема флуктуации
- Отношения Грина – Кубо
- Групповая задержка
- Интрамодальная дисперсия
- Отношения Крамерса – Кронига
- Функция линейного отклика
- Теория дисперсии множественных призм
- Уравнение Селлмейера
- Ультракороткий импульс
- Фазированная решетка с виртуальным изображением
использованная литература
- ^ Родился, Макс; Вольф, Эмиль (октябрь 1999 г.). Принципы оптики. Кембридж: Издательство Кембриджского университета. стр.14 –24. ISBN 0-521-64222-1.
- ^ Компенсация дисперсии Проверено 25 августа 2015.
- ^ Расчет средней дисперсии стекол.
- ^ Борн М. и Вольф Э. (1980) "Принципы оптики, 6-е изд. "Стр. 93. Pergamon Press.
- ^ Салех, Б.Е.А. и Teich, M.C. Основы фотоники (2-е издание) Wiley, 2007.
- ^ Рамасвами, Раджив и Шивараджан, Кумар Н. (1998) Оптические сети: практическая перспектива. Академическая пресса: Лондон.
- ^ Хроматическая дисперсия, Энциклопедия лазерной физики и техники (Wiley, 2008).
- ^ а б Ландау, Л.; Лифшиц, Э.; Питаевский, Л. (1984). Электродинамика сплошных сред.. 8 (2-е изд.). Баттерворт-Хайнеманн. ISBN 978-0-7506-2634-7.
- ^ Demetriadou, A .; Пендри, Дж. Б. (1 июля 2008 г.). «Сдерживание пространственной дисперсии в проволочном метаматериале». Журнал физики: конденсированное вещество. 20 (29): 295222. Bibcode:2008JPCM ... 20C5222D. Дои:10.1088/0953-8984/20/29/295222.
- ^ а б Шуман, Вальтер (2009). Драгоценные камни мира: недавно переработанное и расширенное четвертое издание. Sterling Publishing Company, Inc., стр. 41–2. ISBN 978-1-4027-6829-3. Получено 31 декабря 2011.
- ^ "Что такое дисперсия драгоценных камней?". GemSociety.org. Международное общество драгоценных камней. Получено 2015-03-09.
- ^ Радиоастрономия с одной тарелкой: методы и приложения, Материалы конференции ASP, Vol. 278. Под редакцией Снежаны Станимирович, Даниэль Альтшулер, Пол Голдсмит и Крис Солтер. ISBN 1-58381-120-6. Сан-Франциско: Тихоокеанское астрономическое общество, 2002, стр. 251–269
- ^ Лоример, Д.Р., и Крамер, М., Справочник по пульсарной астрономии, т. 4 Кембриджских справочников по наблюдениям для астрономов-исследователей, (Издательство Кембриджского университета, Кембридж, Великобритания; Нью-Йорк, США, 2005), 1-е издание.
внешняя ссылка
- Дисперсивная вики - обсуждение математических аспектов дисперсии.
- Дисперсия - Энциклопедия лазерной физики и техники
- Анимации, демонстрирующие оптическую дисперсию по QED
- Интерактивная веб-демонстрация хроматической дисперсии Институт телекоммуникаций, Штутгартский университет














