Дуальность волна-частица - Wave–particle duality

Часть серии на
Квантовая механика

Дуальность волна-частица это концепция в квантовая механика что каждый частица или же квант сущность может быть описана как частица или как волна. Он выражает неспособность классический понятия «частица» или «волна», чтобы полностью описать поведение квантовый масштаб объекты. В качестве Альберт Эйнштейн написал:[1]

Кажется, что мы должны иногда использовать одну теорию, а иногда - другую, а иногда мы можем использовать любую из них. Мы столкнулись с трудностями нового типа. У нас есть две противоречивые картины реальности; по отдельности ни один из них полностью не объясняет явления света, но вместе они делают.

Благодаря работе Макс Планк, Альберт Эйнштейн, Луи де Бройль, Артур Комптон, Нильс Бор и многие другие, современная научная теория утверждает, что все частицы обладают волновой природой и наоборот.[2] Это явление было проверено не только для элементарных частиц, но и для составных частиц, таких как атомы и даже молекулы. За макроскопический частицы, из-за их чрезвычайно короткой длины волны, волновые свойства обычно не могут быть обнаружены.[3]

Хотя использование дуальности волна-частица хорошо зарекомендовало себя в физике, его значение или интерпретация не были удовлетворительно решены; видеть Интерпретации квантовой механики.

Бор считал "двойственность парадокс «как фундаментальный или метафизический факт природы. Квантовый объект данного типа будет иногда проявлять волновой, иногда частичный характер в соответственно различных физических условиях. Он видел такую ​​двойственность как один из аспектов концепции взаимодополняемость.[4] Бор считал отказ от причинно-следственной связи или дополнительности пространственно-временной картины существенным для квантово-механического объяснения.[5]

Вернер Гейзенберг рассмотрел вопрос дальше. Он видел, что двойственность присутствует во всех квантовых сущностях, но не совсем в обычном квантово-механическом объяснении, рассматриваемом Бором. Он видел это в том, что называется второе квантование, который порождает совершенно новую концепцию полей, существующих в обычном пространстве-времени, причем причинность все еще можно визуализировать. Классические значения поля (например, напряженность электрического и магнитного поля Максвелл ) заменяются совершенно новым типом значения поля, как рассмотрено в квантовая теория поля. С другой стороны, обычную квантовую механику можно вывести как специализированное следствие квантовой теории поля.[6][7]

История

Классические частицы и волновые теории света

Эскиз Томаса Янга двухщелевая дифракция волн, 1803

Демокрит (V век до нашей эры) утверждал, что все во Вселенной, включая свет, состоят из неделимых компонентов.[8] Евклид (IV-III века до н.э.) дает трактаты о распространении света, утверждает принцип кратчайшей траектории света, включая множественные отражения от зеркал, в том числе сферических, в то время как Плутарх (1-2 века нашей эры) описывает множественные отражения на сферических зеркалах, обсуждая создание больших или меньших изображений, реальных или воображаемых, включая случай хиральность изображений. В начале XI века арабский ученый Ибн аль-Хайсам написал первую исчерпывающую Книга оптики описание отражение, преломление, и действие линзы-обскуры через лучи света, проходящие от точки излучения к глазу. Он утверждал, что эти лучи состоят из частиц света. В 1630 г. Рене Декарт популяризировал и аккредитовал описание противоположной волны в своем трактате о свете, Мир (Декарт), показывая, что поведение света можно воссоздать, моделируя волновые возмущения в универсальной среде, т.е. светоносный эфир. Начиная с 1670 года и продолжаясь более трех десятилетий, Исаак Ньютон разработал и отстаивал свой корпускулярная теория утверждая, что идеально прямые линии отражения демонстрируют природу световых частиц, только частицы могут перемещаться по таким прямым линиям. Он объяснил преломление тем, что частицы света ускоряются вбок, попадая в более плотную среду. Примерно в то же время современники Ньютона Роберт Гук и Кристиан Гюйгенс, и позже Огюстен-Жан Френель, математически уточнил волновую точку зрения, показав, что если свет движется с разной скоростью в разных средах, преломление можно легко объяснить как распространение световых волн в зависимости от среды. Результирующий Принцип Гюйгенса – Френеля был чрезвычайно успешным в воспроизведении поведения света и впоследствии был поддержан Томас Янг открытие волновая интерференция света его двухщелевой эксперимент в 1801 г.[9][10] Волновое представление не сразу вытеснило представление о лучах и частицах, но начало доминировать в научных размышлениях о свете в середине 19 века, поскольку оно могло объяснить явления поляризации, которые не могли дать альтернативы.[11]

Джеймс Клерк Максвелл обнаружил, что может применить свои ранее открытые Уравнения Максвелла, наряду с небольшой модификацией для описания самораспространяющихся волн осциллирующих электрических и магнитных полей. Быстро стало очевидно, что видимый свет, ультрафиолетовый свет и инфракрасный свет представляют собой электромагнитные волны разной частоты.

Излучение черного тела и закон Планка

Основная статья: Излучение черного тела

В 1901 г. Макс Планк опубликовали анализ, в котором удалось воспроизвести наблюдаемые спектр света, излучаемого светящимся объектом. Для этого Планку пришлось сделать математическое предположение о квантованной энергии осцилляторов, то есть атомов черное тело которые испускают радиацию. Позднее Эйнштейн предположил, что квантуется само электромагнитное излучение, а не энергия излучающих атомов.

Излучение черного тела, излучение электромагнитной энергии из-за тепла объекта, нельзя объяснить с помощью одних лишь классических аргументов. В теорема о равнораспределении классической механики, основы всех классических термодинамических теорий, утверждали, что энергия объекта равномерно распределяется между колебательными движениями объекта. режимы. Но применить те же рассуждения к электромагнитному излучению такого теплового объекта не удалось. То, что тепловые объекты излучают свет, было известно давно. Поскольку было известно, что свет является волнами электромагнетизма, физики надеялись описать это излучение с помощью классических законов. Это стало известно как проблема черного тела. Поскольку теорема о равнораспределении так хорошо сработала при описании колебательных мод самого теплового объекта, было естественным предположить, что она будет одинаково хорошо работать и при описании излучения таких объектов. Но проблема быстро возникала, если каждая мода получала равное распределение энергии, коротковолновые моды потребляли бы всю энергию. Это стало ясно при построении графика Закон Рэлея – Джинса, который, правильно предсказывая интенсивность длинноволновых излучений, предсказал бесконечную полную энергию, поскольку интенсивность расходится до бесконечности для коротких волн. Это стало известно как ультрафиолетовая катастрофа.

В 1900 году Макс Планк выдвинул гипотезу о том, что частота света, излучаемого черным телом, зависит от частоты генератора, который его излучает, и энергия этих осцилляторов линейно возрастает с частотой (согласно E = hf куда час постоянная Планка и ж это частота). Это не было ошибочным предположением, учитывая, что макроскопические осцилляторы работают аналогично при изучении пяти простые гармонические осцилляторы с одинаковой амплитудой, но разной частотой, осциллятор с самой высокой частотой обладает самой высокой энергией (хотя это соотношение не является линейным, как у Планка). Требуя, чтобы высокочастотный свет излучался генератором одинаковой частоты, и дополнительно требуя, чтобы этот генератор занимал большую энергию, чем один из более низких частот, Planck избежал любой катастрофы, предоставив равное разделение высокочастотным генераторам, производящим последовательно меньше генераторы и менее излучаемый свет. И как в Распределение Максвелла – Больцмана, низкочастотные генераторы с низкой энергией подавлялись натиском тепловых колебаний со стороны генераторов с более высокой энергией, что неизбежно увеличивало их энергию и частоту.

Самый революционный аспект трактовки черного тела Планком заключается в том, что оно по своей сути полагается на целое число осцилляторов в тепловое равновесие с электромагнитным полем. Эти осцилляторы отдают всю свою энергию электромагнитному полю, создавая квант света так часто, как они возбуждаются электромагнитным полем, поглощая квант света и начиная колебаться с соответствующей частотой. Планк намеренно создал атомную теорию черного тела, но непреднамеренно создал атомную теорию света, согласно которой черное тело никогда не генерирует кванты света заданной частоты с энергией меньше hf. Однако, однажды осознав, что он квантовал электромагнитное поле, он объявил частицы света ограничением своего приближения, а не свойством реальности.

Фотоэлектрический эффект

Основная статья: Фотоэлектрический эффект
Фотоэлектрический эффект. Входящие слева фотоны ударяются о металлическую пластину (внизу) и выбрасывают электроны, которые изображены летящими справа.

В то время как Планк решил ультрафиолетовую катастрофу с помощью атомов и квантованного электромагнитного поля, большинство современных физиков согласились с тем, что «кванты света» Планка представляют собой лишь недостатки его модели. Более полный вывод излучения черного тела даст полностью непрерывное и «волнообразное» электромагнитное поле без квантования. Однако в 1905 г. Альберт Эйнштейн использовал модель черного тела Планка, чтобы найти решение еще одной выдающейся проблемы дня: фотоэлектрический эффект, в котором электроны испускаются атомами, когда они поглощают энергию света. Поскольку их существование теоретизировалось восемь лет назад, явления изучались с учетом электронной модели в физических лабораториях по всему миру.

В 1902 г. Филипп Ленард обнаружили, что энергия этих выброшенных электронов не зависит от интенсивности падающего света, а зависит от его частоты. Итак, если направить на металл небольшой низкочастотный свет, несколько электронов с низкой энергией выбрасываются. Если сейчас направить очень интенсивный луч низкочастотного света на тот же металл, выбросится целая серия электронов; однако они обладают такой же низкой энергией, их просто больше. Чем больше света, тем больше электронов выбрасывается. Тогда как для получения электронов высокой энергии нужно осветить металл высокочастотным светом. Как и излучение абсолютно черного тела, это противоречило теории, предполагающей непрерывный перенос энергии между излучением и веществом. Тем не менее, это все еще можно объяснить, используя полностью классическое описание света, если материя является квантово-механической по своей природе.[12]

Если бы кто-то использовал кванты энергии Планка и потребовал, чтобы электромагнитное излучение на данной частоте могло передавать энергию материи только в целых кратных величинах кванта энергии hf, то фотоэлектрический эффект можно было бы очень просто объяснить. Низкочастотный свет излучает только электроны с низкой энергией, потому что каждый электрон возбуждается поглощением одного фотона. Увеличение интенсивности низкочастотного света (увеличение количества фотонов) увеличивает только количество возбужденных электронов, но не их энергию, потому что энергия каждого фотона остается низкой. Только увеличивая частоту света и, таким образом, увеличивая энергию фотонов, можно выбрасывать электроны с более высокой энергией. Таким образом, используя постоянную Планка час чтобы определить энергию фотонов на основе их частоты, энергия выброшенных электронов должна также линейно увеличиваться с частотой, градиент линии является постоянной Планка. Эти результаты не были подтверждены до 1915 г., когда Роберт Эндрюс Милликен дала экспериментальные результаты, полностью согласующиеся с предсказаниями Эйнштейна.

Хотя энергия выброшенных электронов отражала постоянную Планка, существование фотонов не было явно доказано до открытия антигруппировка фотонов эффект, из которого современный эксперимент может быть проведен в лабораториях уровня бакалавриата.[13] Это явление можно было объяснить только с помощью фотонов. "Кванты света" Эйнштейна нельзя было бы назвать фотоны до 1925 г., но даже в 1905 г. они представляли типичный пример дуальности волна-частица. Электромагнитное излучение распространяется в соответствии с линейными волновыми уравнениями, но может излучаться или поглощаться только как дискретные элементы, таким образом действуя как волна и частица одновременно.

Объяснение фотоэлектрического эффекта Эйнштейном

В 1905 году Альберт Эйнштейн дал объяснение фотоэлектрическому эффекту, эксперименту, который волновая теория света не смогла объяснить. Он сделал это, постулировав существование фотонов, кванты световой энергии с качеством твердых частиц.

в фотоэлектрический эффект было замечено, что попадание света на некоторые металлы может привести к электрический ток в схема. Предположительно, свет выбивал электроны из металла, вызывая протекание тока. Однако, используя случай калия в качестве примера, было также замечено, что хотя тусклого синего света было достаточно, чтобы вызвать ток, даже самый сильный, самый яркий красный свет, доступный с технологией того времени, не вызывал тока вообще. Согласно классической теории света и материи, сила или амплитуда Световая волна была пропорциональна ее яркости: яркий свет должен был быть достаточно сильным, чтобы создать большой ток. Однако, как ни странно, это было не так.

Эйнштейн объяснил эту загадку тем, что постулирование что электроны могут получать энергию от электромагнитного поля только в дискретных единицах (кванты или фотоны): количество энергия E это было связано с частота ж света

куда час является Постоянная Планка (6.626 × 10−34 Js). Только фотоны достаточно высокой частоты (выше определенного порог значение) может выбить электрон на свободу. Например, фотоны синего света обладали достаточной энергией, чтобы освободить электрон от металла, а фотоны красного света - нет. Один фотон света с частотой выше пороговой может высвободить только один электрон; чем выше частота фотона, тем выше кинетическая энергия испускаемого электрона, но никакое количество света ниже пороговой частоты не может высвободить электрон. Для нарушения этого закона потребовались бы лазеры очень высокой интенсивности, которые еще не были изобретены. Явления, зависящие от интенсивности, теперь подробно изучены с помощью таких лазеров.[14]

Эйнштейн был награжден Нобелевская премия по физике в 1921 г. за открытие закона фотоэффекта.

гипотеза де Бройля

Основная статья: Волна материи
Распространение волны де Бройля в 1г - действительная часть сложный амплитуда синяя, мнимая часть зеленая. Вероятность (показана цветом непрозрачность ) нахождения частицы в заданной точке Икс распространяется как форма волны; нет определенного положения частицы. При увеличении амплитуды выше нуля кривизна уменьшается, поэтому амплитуда снова уменьшается, и наоборот - в результате возникает переменная амплитуда: волна. Вершина: Плоская волна. Нижний: Волновой пакет.

В 1924 г. Луи-Виктор де Бройль сформулировал гипотеза де Бройля, утверждая, что все имеет значение[15][16] имеет волнообразный характер, рассказал он длина волны и импульс:

Это обобщение приведенного выше уравнения Эйнштейна, поскольку импульс фотона определяется выражением п = а длину волны (в вакууме) на λ = , куда c это скорость света в вакууме.

Формула Де Бройля была подтверждена три года спустя для электроны с наблюдением за электронная дифракция в двух независимых экспериментах. На Университет Абердина, Джордж Пэджет Томсон пропускал пучок электронов через тонкую металлическую пленку и наблюдал предсказанные интерференционные картины. В Bell Labs, Клинтон Джозеф Дэвиссон и Лестер Халберт Гермер направили электронный луч через кристаллическую решетку в своем эксперименте, широко известном как Эксперимент Дэвиссона-Гермера.

Де Бройль был награжден Нобелевская премия по физике в 1929 г. за свою гипотезу. Томсон и Дэвиссон разделили Нобелевскую премию по физике в 1937 году за свои экспериментальные работы.

Принцип неопределенности Гейзенберга

Основная статья: Принцип неопределенности

В своей работе по формулировке квантовой механики, Вернер Гейзенберг постулировал свой принцип неопределенности, который гласит:

куда

здесь указывает стандартное отклонение, мера разброса или неопределенности;
Икс и п положение частицы и линейный импульс соответственно.
это приведенная постоянная Планка (Постоянная Планка, деленная на 2).

Первоначально Гейзенберг объяснил это следствием процесса измерения: точное измерение положения может нарушить импульс, и наоборот, предлагая пример («гамма-микроскоп»), который в решающей степени зависит от гипотеза де Бройля. Однако сейчас думают, что это лишь частично объясняет явление, но что неопределенность существует также в самой частице, даже до того, как будет произведено измерение.

Фактически, современное объяснение принципа неопределенности, расширяющее Копенгагенская интерпретация впервые выдвинут Бор и Гейзенберг, еще в большей степени зависит от волновой природы частицы. Точно так же, как бессмысленно обсуждать точное положение волны на струне, частицы не имеют совершенно точных положений; точно так же, как бессмысленно обсуждать длину волны «импульсной» волны, бегущей по струне, частицы не имеют совершенно точных импульсов, которые соответствуют обратной длине волны. Более того, когда положение относительно хорошо определено, волна имеет форму импульса и имеет очень плохо определенную длину волны и, следовательно, импульс. И наоборот, когда импульс и, следовательно, длина волны относительно хорошо определены, волна выглядит длинной и синусоидальной, и, следовательно, ее положение очень нечеткое.

теория де Бройля – Бома

Основная статья: теория де Бройля – Бома
Кудер эксперименты,[17] "материализация" пилотная волна модель.

Сам Де Бройль предложил пилотная волна построить, чтобы объяснить наблюдаемый дуализм волна-частица. С этой точки зрения каждая частица имеет четко определенное положение и импульс, но управляется волновой функцией, полученной из Уравнение Шредингера. Теория пилотной волны была первоначально отвергнута, поскольку она генерировала нелокальные эффекты при применении к системам, включающим более одной частицы. Однако нелокальность вскоре стала неотъемлемой чертой квантовая теория и Дэвид Бом расширила модель де Бройля, чтобы явно включить ее.

В полученном представлении, также называемом теория де Бройля – Бома или бомовская механика,[18] дуальность волна-частица исчезает и объясняет поведение волны как рассеяние с появлением волны, потому что движение частицы подчиняется ведущему уравнению или квантовый потенциал.

Эта идея кажется мне настолько естественной и простой - разрешить дилемму волна – частица таким ясным и обычным способом, что для меня большая загадка, что ее так часто игнорировали.[19] – Дж. С. Белл

Лучшая иллюстрация пилотно-волновая модель было получено в экспериментах Кудера 2010 года с «шагающими каплями»,[20] демонстрируя поведение пилот-волны в макроскопическом механическом аналоге.[17]

Волновой характер крупных объектов

Поскольку демонстрация волнообразных свойств в фотоны и электроны, аналогичные эксперименты проводились с нейтроны и протоны. Среди самых известных экспериментов - эксперименты Эстерманн и Отто Стерн в 1929 г.[21]Авторы аналогичных недавних экспериментов с атомами и молекулами, описанных ниже, утверждают, что эти более крупные частицы также действуют как волны.

Драматическая серия экспериментов, подчеркивающих действие сила тяжести применительно к дуальности волна – частица была проведена в 1970-х годах с использованием нейтронный интерферометр.[22] Нейтроны, одна из составляющих атомное ядро, обеспечивают большую часть массы ядра и, следовательно, массы обычного вещества. В нейтронном интерферометре они действуют как квантово-механические волны, непосредственно подверженные силе тяжести. Хотя результаты не были удивительными, поскольку было известно, что гравитация действует на все, включая свет (см. тесты общей теории относительности и Эксперимент с падающим фотоном Паунда – Ребки ) самоинтерференция квантово-механической волны массивной фермион в гравитационном поле никогда ранее не подтверждалось экспериментально.

В 1999 г. дифракция C60 фуллерены исследователями из Венский университет Сообщалось.[23] Фуллерены - сравнительно большие и массивные объекты, имеющие атомную массу около 720 ты. В длина волны де Бройля падающего луча составляла около 2,5вечера, тогда как диаметр молекулы около 1нм, примерно в 400 раз больше. В 2012 году эти эксперименты по дифракции в дальней зоне могут быть расширены до фталоцианин молекулы и их более тяжелые производные, которые состоят из 58 и 114 атомов соответственно. В этих экспериментах нарастание таких интерференционных картин можно было регистрировать в реальном времени и с чувствительностью к отдельной молекуле.[24]

В 2003 году Венская группа также продемонстрировала волновую природу тетрафенилпорфирин[25]- плоский биодобавок протяженностью около 2 нм и массой 614 ед. Для этой демонстрации они использовали ближнее поле Интерферометр Тальбота-Лау.[26][27] В том же интерферометре были обнаружены интерференционные полосы для C60F48., фторированный Buckyball с массой около 1600 u, состоящий из 108 атомов.[25] Большие молекулы уже настолько сложны, что дают экспериментальный доступ к некоторым аспектам квантово-классического интерфейса, т. Е. К определенным декогеренция механизмы.[28][29] В 2011 г. интерференция молекул весом до 6910 u могла быть продемонстрирована на интерферометре Капицы – Дирака – Тальбота – Лау.[30] В 2013 году было продемонстрировано вмешательство молекул за пределами 10 000 ед.[31]

Будь то предметы тяжелее Планковская масса (о весе большой бактерии) иметь длину волны де Бройля теоретически неясно и экспериментально недостижимо; над массой Планка частицы Комптоновская длина волны будет меньше, чем Планковская длина и свой Радиус Шварцшильда, масштаб, на котором современные теории физики могут сломаться или должны быть заменены более общими.[32]

Недавно Couder, Fort, и другие. показал[33] что мы можем использовать макроскопические масляные капли на вибрирующей поверхности в качестве модели дуальности волна-частица - локализованная капля создает периодические волны вокруг, и взаимодействие с ними приводит к квантовоподобным явлениям: интерференция в эксперименте с двумя щелями,[34] непредсказуемое туннелирование[35] (в зависимости от практически скрытого состояния поля), квантование орбиты[36] (эта частица должна «найти резонанс» с возмущениями поля, которые она создает - после одного витка ее внутренняя фаза должна вернуться в исходное состояние) и Эффект Зеемана.[37]

Важность

Дуальность волна-частица глубоко укоренилась в основе квантовая механика. в формализм теории, вся информация о частице закодирована в ее волновая функция, комплексная функция, примерно аналогичная амплитуде волны в каждой точке пространства. Эта функция развивается согласно Уравнение Шредингера. Для частиц с массой это уравнение имеет решения, которые повторяют форму волнового уравнения. Распространение таких волн приводит к подобным волнам явлениям, таким как интерференция и дифракция. Частицы без массы, как фотоны, не имеют решений уравнения Шредингера, поэтому у них есть другая волна.

Подобное частицам поведение наиболее очевидно из-за явлений, связанных с измерение в квантовой механике. После измерения местоположения частицы она будет переведена в более локализованное состояние в соответствии с принципом неопределенности. Если смотреть через этот формализм, измерение волновой функции случайным образом приведет к коллапс волновой функции к резко выраженной функции в некотором месте. Для частиц с массой вероятность обнаружения частицы в любом конкретном месте равна квадрату амплитуды волновой функции там. Измерение вернет четко определенное положение и зависит от Принцип неопределенности Гейзенберга.

После разработки квантовая теория поля двусмысленность исчезла. Поле допускает решения, которые следуют волновому уравнению, которые называются волновыми функциями. Термин частица используется для обозначения неприводимых представлений Группа Лоренца что разрешено полем. Взаимодействие как в Диаграмма Фейнмана принимается в качестве удобного в расчетном отношении приближения, в котором исходящие ветви известны как упрощения распространения, а внутренние линии служат для некоторого порядка в разложении полевого взаимодействия. Поскольку поле нелокально и квантовано, объясняются явления, которые раньше считались парадоксами. В рамках дуализма волна-частица квантовая теория поля дает те же результаты.

Визуализация

Есть два способа визуализировать поведение волны-частицы: с помощью стандартной модели и по теории де Бройля – Бора.

Ниже приведена иллюстрация дуальности волна-частица в связи с гипотезой де Бройля и принципом неопределенности Гейзенберга в терминах пространственных волновых функций положения и импульса для одной бесспиновой частицы с массой в одном измерении. Эти волновые функции Преобразования Фурье друг друга.

Чем более локализована волновая функция в пространственно-позиционном пространстве, тем более вероятно, что частица будет обнаружена с координатами положения в этой области, и, соответственно, волновая функция в импульсном пространстве менее локализована, поэтому возможные компоненты импульса, которые могла бы иметь частица, более распространены.

И наоборот, чем более локализована волновая функция в пространстве импульсов, тем больше вероятность того, что частица будет обнаружена с такими значениями компонент импульса в этой области, и, соответственно, тем менее локализована волновая функция в пространстве координат, поэтому координаты положения, которые может занимать частица, равны более распространенный.

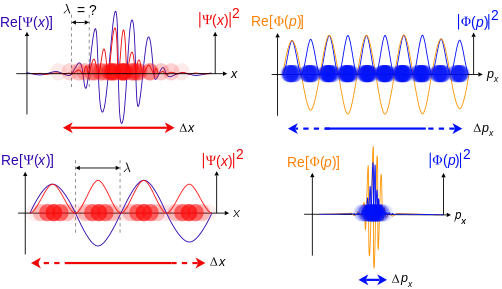
Позиция Икс и импульс п волновые функции, соответствующие квантовым частицам. Цветовая непрозрачность частиц соответствует плотность вероятности найти частицу с положением Икс или компонент импульса п.
Вершина: Если длина волны λ неизвестно, так что импульс п, волновой вектор k и энергия E (отношения де Бройля). Поскольку частица более локализована в позиционном пространстве, ΔИкс меньше, чем при ΔпИкс.
Нижний: Если λ известно, так же п, k, и E. Поскольку частица более локализована в импульсном пространстве, Δп меньше, чем при ΔИкс.

Альтернативные виды

Двойственность волна-частица - постоянная загадка современной физики. Большинство физиков принимают дуализм волна-частица как лучшее объяснение широкого диапазона наблюдаемых явлений; однако это не без противоречий. Здесь также представлены альтернативные виды. Эти взгляды не являются общепринятыми в традиционной физике, но служат основой для ценных обсуждений в сообществе.

Вид как частицы, так и волны

В пилотная волна модель, первоначально разработанная Луи де Бройль и далее развито Дэвид Бом в теория скрытых переменных предполагает, что нет никакой двойственности, а скорее система демонстрирует свойства частиц и волновые свойства одновременно, и частицы направляются в детерминированный моды, пилотной волной (или ее "квантовый потенциал "), который направит их в районы конструктивное вмешательство предпочтение районам деструктивное вмешательство. Этой идеей придерживается значительное меньшинство в физическом сообществе.[38]

По крайней мере, один физик считает, что «волновая дуальность» не является непостижимой загадкой. L.E. Баллентин, Квантовая механика, современное развитие (1989), стр. 4 поясняет:

Когда впервые было обнаружено, дифракция частиц была источником большого недоумения. Действительно ли «частицы» являются «волнами»? В ранних экспериментах дифракционные картины регистрировались целиком с помощью фотографической пластинки, которая не могла обнаруживать отдельные частицы. В результате росло представление о том, что частицы и волновые свойства несовместимы или дополняют друг друга в том смысле, что для их наблюдения потребуются разные измерительные устройства. Однако эта идея была лишь неудачным обобщением технологических ограничений. Сегодня можно регистрировать приход отдельных электронов и видеть, как дифракционная картина возникает как статистическая картина, состоящая из множества маленьких пятен (Tonomura et al., 1989). Очевидно, что квантовые частицы действительно являются частицами, но поведение которых сильно отличается от классической физики, можно ожидать.

В Афшар эксперимент[39] (2007) могут предположить, что можно одновременно наблюдать как волновые, так и частичные свойства фотонов. Однако это утверждение оспаривается другими учеными.[40][41][42][43]

Просмотр только волны

Карвер Мид, американский ученый и профессор Калифорнийского технологического института, предполагает, что двойственность может быть заменена взглядом "только волны". В его книге Коллективная электродинамика: квантовые основы электромагнетизма (2000), Мид пытается проанализировать поведение электроны и фотоны чисто в терминах электронных волновых функций, и приписывает кажущееся поведение, подобное частицам, эффектам квантования и собственным состояниям. По словам обозревателя Дэвида Хэддона:[44]

Мид сократил гордиев узел квантовой дополнительности. Он утверждает, что атомы с их нейтронами, протонами и электронами - это вовсе не частицы, а чистые волны материи. Мид приводит в качестве грубого доказательства исключительно волновой природы как света, так и материи открытие между 1933 и 1996 годами десяти примеров чисто волновых явлений, включая повсеместное применение лазера CD проигрыватели, самораспространяющиеся электрические токи сверхпроводники, а Конденсат Бозе – Эйнштейна атомов.

Альберт Эйнштейн, который в поисках Единая теория поля, не принимал дуальность волна-частица, писал:[45]

Эта двойная природа излучения (и материальных корпускул) ... была интерпретирована квантовой механикой гениальным и удивительно успешным образом. Эта интерпретация ... кажется мне лишь временным выходом ...

В многомировая интерпретация (MWI) иногда представляется как теория только волн, в том числе ее создателем, Хью Эверетт который назвал MWI «волновой интерпретацией».[46]

В трехволновая гипотеза Р. Городецкого связывает частицу с волной.[47][48] Гипотеза подразумевает, что массивная частица является внутренне пространственным, а также временным волновым явлением по нелинейному закону.

В детерминированная теория коллапса[49] рассматривает коллапс и измерение как два независимых физических процесса. Коллапс происходит, когда два волновых пакета пространственно перекрываются и удовлетворяют математическому критерию, который зависит от параметров обоих волновых пакетов. Это сокращение объема перекрытия. В измерительном устройстве один из двух волновых пакетов является одним из атомных кластеров, составляющих устройство, и волновые пакеты коллапсируют до максимального объема такого кластера. Это имитирует действие точечной частицы.

Просмотр только для частиц

Еще в дни старая квантовая теория доквантово-механическая версия дуальности волна-частица была впервые предложена Уильям Дуэйн,[50] и разработан другими, включая Альфред Ланде.[51] Дуэйн объяснил дифракцию рентгеновские лучи кристаллом исключительно с точки зрения их частиц. Отклонение траектории каждого дифрагированного фотона объяснялось тем, что квантованная передача импульса от пространственно регулярной структуры дифрагирующего кристалла.[52]

Ни волны, ни частицы

Утверждалось, что никогда не бывает точных частиц или волн, а есть лишь некоторый компромисс или промежуточное звено между ними. По этой причине в 1928 г. Артур Эддингтон[53] придумал название "волнистость«для описания объектов, хотя сегодня он не используется регулярно. математические очки нельзя наблюдать. Другой заключается в том, что формальное представление таких точек, Дельта-функция Дирака нефизичен, потому что не может быть нормализованный. Параллельные аргументы применимы к чистым волновым состояниям. Роджер Пенроуз состояния:[54]

Такие «состояния положения» являются идеализированными волновыми функциями в противоположном смысле от импульсных состояний. В то время как состояния импульса бесконечно распределены, состояния положения бесконечно сконцентрированы. Ни то, ни другое нельзя нормализовать [...].

Реляционный подход к дуальности волна – частица

Реляционная квантовая механика был разработан как точка зрения, согласно которой событие обнаружения частицы устанавливает связь между квантованным полем и детектором. Следовательно, исключается присущая двусмысленности, связанная с применением принципа неопределенности Гейзенберга; следовательно, нет дуальности волна-частица.[55]

Использует

Хотя трудно провести черту, отделяющую дуальность волна-частица от остальной части квантовой механики, тем не менее можно перечислить некоторые приложения этой основной идеи.

  • Двойственность волна – частица используется в электронная микроскопия, где небольшие длины волн, связанные с электроном, могут использоваться для просмотра объектов, намного меньших, чем то, что видно при использовании видимого света.
  • По аналогии, нейтронография использует нейтроны с длиной волны около 0,1нм, типичное расстояние между атомами в твердом теле, чтобы определить структуру твердого тела.
  • Фотографии теперь могут показать эту двойственную природу, что может привести к новым способам изучения и записи этого поведения.[56]

Смотрите также

Рекомендации

  1. ^ Альберт Эйнштейн, Леопольд Инфельд (1938). Эволюция физики: рост идей от ранних концепций до теории относительности и квантов. Издательство Кембриджского университета. Bibcode:1938epgi.book ..... E.CS1 maint: использует параметр авторов (связь)Цитируется в Харрисон, Дэвид (2002). «Дополнительность и копенгагенская интерпретация квантовой механики». НАБОР. Департамент физики Университета Торонто. Получено 2008-06-21.
  2. ^ Уолтер Грейнер (2001). Квантовая механика: введение. Springer. ISBN  978-3-540-67458-0.
  3. ^ Р. Айсберг и Р. Резник (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Джон Вили и сыновья. стр.59–60. ISBN  978-0-471-87373-0. И для больших, и для малых длин волн и материя, и излучение имеют как частицы, так и волновые аспекты ... Но волновые аспекты их движения становится труднее наблюдать по мере того, как их длины волн становятся короче ... Для обычных макроскопических частиц масса такова. велика, что импульс всегда достаточно велик, чтобы длина волны де Бройля была достаточно малой, чтобы выйти за пределы диапазона экспериментального обнаружения, и классическая механика господствует.
  4. ^ Кумар, Манджит (2011). Квантовая: Эйнштейн, Бор и великие дебаты о природе реальности (Перепечатка ред.). W. W. Norton & Company. стр.242, 375–376. ISBN  978-0-393-33988-8.
  5. ^ Бор, Н. (1928). «Квантовый постулат и недавнее развитие атомной теории». Природа. 121 (3050): 580–590. Bibcode:1928Натура.121..580Б. Дои:10.1038 / 121580a0.
  6. ^ Камиллери, К. (2009). Гейзенберг и интерпретация квантовой механики: физик как философ, Издательство Кембриджского университета, Кембридж, Великобритания, ISBN  978-0-521-88484-6.
  7. ^ Препарата, Г. (2002). Введение в реалистичную квантовую физику, World Scientific, Ривер Эдж, штат Нью-Джерси, ISBN  978-981-238-176-7.
  8. ^ Натаниэль Пейдж Стайтс, M.A./M.S. «Свет I: частица или волна?», Visionlearning Vol. PHY-1 (3), 2005. http://www.visionlearning.com/library/module_viewer.php?mid=132
  9. ^ Янг, Томас (1804). «Бейкерская лекция: эксперименты и расчеты в области физической оптики». Философские труды Королевского общества. 94: 1–16. Bibcode:1804РСПТ ... 94 .... 1Л. Дои:10.1098 / рстл.1804.0001. S2CID  110408369.
  10. ^ Томас Янг: эксперимент с двойной щелью
  11. ^ Бухвальд, Джед (1989). Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века. Чикаго: Издательство Чикагского университета. ISBN  978-0-226-07886-1. OCLC  18069573.
  12. ^ Лэмб, Уиллис Э.; Скалли, Марлан О. (1968). «Фотоэффект без фотонов» (PDF).
  13. ^ Thorn, J. J .; Neel, M. S .; Донато, В. З .; Бергрин, Г. С .; Дэвис, Р. Э .; Бек, М. (2004). «Наблюдение за квантовым поведением света в студенческой лаборатории». Американский журнал физики. 72 (9): 1210. Bibcode:2004AmJPh..72.1210T. Дои:10.1119/1.1737397.
  14. ^ Чжан, Q (1996). «Зависимость от интенсивности фотоэлектрического эффекта, индуцированного лазерным лучом с круговой поляризацией». Письма о физике A. 216 (1–5): 125–128. Bibcode:1996ФЛА..216..125З. Дои:10.1016/0375-9601(96)00259-9.
  15. ^ Дональд Х. Мензель "Основные формулы физики", vol. 1, p. 153; Даны длины волн де Бройля для составных частиц, таких как протоны и нейтроны.
  16. ^ Брайан Грин, Элегантная Вселенная, стр. 104 «вся материя имеет волнообразный характер»
  17. ^ а б См. Выпуск этого научного канала (Сезон II, Эпизод VI «Как устроена Вселенная?»), Представленный Морганом Фриманом, https://www.youtube.com/watch?v=W9yWv5dqSKk
  18. ^ Бомская механика, Стэнфордская энциклопедия философии.
  19. ^ Белл, Дж. С., «Говоримое и невыразимое в квантовой механике», Кембридж: Издательство Кембриджского университета, 1987.
  20. ^ Кудер, Ю. (2010). «Бегущие капли, форма дуальности волна-частица в макроскопическом масштабе?» (PDF). Новости Europhysics. 41 (1): 14–18. Bibcode:2010ENews..41a..14C. Дои:10.1051 / epn / 2010101.
  21. ^ Estermann, I .; Стерн О. (1930). "Beugung von Molekularstrahlen". Zeitschrift für Physik. 61 (1–2): 95–125. Bibcode:1930ZPhy ... 61 ... 95E. Дои:10.1007 / BF01340293. S2CID  121757478.
  22. ^ Colella, R .; Overhauser, A. W .; Вернер, С. А. (1975). «Наблюдение квантовой интерференции, вызванной гравитацией» (PDF). Письма с физическими проверками. 34 (23): 1472–1474. Bibcode:1975ПхРвЛ..34.1472С. Дои:10.1103 / PhysRevLett.34.1472.
  23. ^ Арндт, Маркус; О. Наирз; J. Voss-Andreae, К. Келлер, Г. ван дер Зоу, А. Цайлингер (14 октября 1999 г.). "Волново-частичная двойственность C60". Природа. 401 (6754): 680–682. Bibcode:1999Натура.401..680А. Дои:10.1038/44348. PMID  18494170. S2CID  4424892.CS1 maint: несколько имен: список авторов (связь)
  24. ^ Юффманн, Томас; и другие. (25 марта 2012 г.). «Визуализация одной молекулы квантовой интерференции в реальном времени». Природа Нанотехнологии. 7 (5): 297–300. arXiv:1402.1867. Bibcode:2012НатНа ... 7..297J. Дои:10.1038 / nnano.2012.34. PMID  22447163. S2CID  5918772.
  25. ^ а б Хаккермюллер, Люсия; Стефан Уттенталер; Клаус Хорнбергер; Элизабет Рейгер; Бьёрн Брезгер; Антон Цайлингер; Маркус Арндт (2003). «Волновая природа биомолекул и фторфуллеренов». Phys. Rev. Lett. 91 (9): 090408. arXiv:Quant-ph / 0309016. Bibcode:2003PhRvL..91i0408H. Дои:10.1103 / PhysRevLett.91.090408. PMID  14525169. S2CID  13533517.
  26. ^ Клаузер, Джон Ф .; С. Ли (1994). «Интерфометрия Тальбота фон Лау с холодными медленными атомами калия». Phys. Ред. А. 49 (4): R2213–2217. Bibcode:1994PhRvA..49.2213C. Дои:10.1103 / PhysRevA.49.R2213. PMID  9910609.
  27. ^ Брезгер, Бьёрн; Люсия Хаккермюллер; Стефан Уттенталер; Юлия Петчинка; Маркус Арндт; Антон Цайлингер (2002). «Интерферометр волны материи для больших молекул». Phys. Rev. Lett. 88 (10): 100404. arXiv:Quant-ph / 0202158. Bibcode:2002PhRvL..88j0404B. Дои:10.1103 / PhysRevLett.88.100404. PMID  11909334. S2CID  19793304.
  28. ^ Хорнбергер, Клаус; Стефан Уттенталер; Бьёрн Брезгер; Люсия Хаккермюллер; Маркус Арндт; Антон Цайлингер (2003). «Наблюдение коллизионной декогеренции в интерферометрии». Phys. Rev. Lett. 90 (16): 160401. arXiv:Quant-ph / 0303093. Bibcode:2003ПхРвЛ..90п0401Н. Дои:10.1103 / PhysRevLett.90.160401. PMID  12731960. S2CID  31057272.
  29. ^ Хаккермюллер, Люсия; Клаус Хорнбергер; Бьёрн Брезгер; Антон Цайлингер; Маркус Арндт (2004). «Декогеренция волн материи тепловым излучением». Природа. 427 (6976): 711–714. arXiv:Quant-ph / 0402146. Bibcode:2004Натура.427..711H. Дои:10.1038 / природа02276. PMID  14973478. S2CID  3482856.
  30. ^ Герлих, Стефан; и другие. (2011). «Квантовая интерференция больших органических молекул». Nature Communications. 2 (263): 263. Bibcode:2011НатКо ... 2..263G. Дои:10.1038 / ncomms1263. ЧВК  3104521. PMID  21468015.
  31. ^ Eibenberger, S .; Герлих, С .; Arndt, M .; Мэр, М .; Тюксен, Дж. (2013). «Материя – волна интерференции частиц, выбранных из молекулярной библиотеки с массами, превышающими 10 000 а.е.м.». Физическая химия Химическая физика. 15 (35): 14696–14700. arXiv:1310.8343. Bibcode:2013PCCP ... 1514696E. Дои:10.1039 / c3cp51500a. PMID  23900710. S2CID  3944699.
  32. ^ Питер Габриэль Бергманн, Загадка гравитации, Courier Dover Publications, 1993 г. ISBN  0-486-27378-4 онлайн
  33. ^ Ив Кудер объясняет двойственность волны / частицы с помощью кремниевых капель - YouTube
  34. ^ Кудер, Ив; Форт, Эммануэль (2006). «Дифракция одиночных частиц и интерференция в макроскопическом масштабе». Письма с физическими проверками. 97 (15): 154101. Bibcode:2006PhRvL..97o4101C. Дои:10.1103 / PhysRevLett.97.154101. PMID  17155330.
  35. ^ Эдди, А .; Fort, E .; Moisy, F .; Кудер, Ю. (2009). «Непредсказуемое туннелирование классической ассоциации волна-частица». Письма с физическими проверками. 102 (24): 240401. Bibcode:2009PhRvL.102x0401E. Дои:10.1103 / PhysRevLett.102.240401. PMID  19658983.
  36. ^ Fort, E .; Эдди, А .; Boudaoud, A .; Moukhtar, J .; Кудер, Ю. (2010). «Квантование классических орбит, вызванное памятью путей». PNAS. 107 (41): 17515–17520. arXiv:1307.6051. Bibcode:2010PNAS..10717515F. Дои:10.1073 / pnas.1007386107. S2CID  53462533.
  37. ^ Эдди, А .; Moukhtar, J .; Perrard, S .; Fort, E .; Кудер, Ю. (2012). «Расщепление уровней в макроскопическом масштабе». Письма с физическими проверками. 108 (26): 264503. Bibcode:2012PhRvL.108z4503E. Дои:10.1103 / PhysRevLett.108.264503. PMID  23004988.
  38. ^ (Бьюкенен, стр. 29–31)
  39. ^ Afshar, S.S .; и другие. (2007). «Парадокс в дуальности волновых частиц». Найденный. Phys. 37 (2): 295. arXiv:Quant-ph / 0702188. Bibcode:2007ФоФ ... 37..295А. Дои:10.1007 / s10701-006-9102-8. S2CID  2161197.
  40. ^ Кастнер, Р. (2005). «Почему эксперимент Афшара не опровергает дополнительности». Исследования по истории и философии науки Часть B: Исследования по истории и философии современной физики. 36 (4): 649–658. arXiv:Quant-ph / 0502021. Bibcode:2005ШПМП..36..649К. Дои:10.1016 / j.shpsb.2005.04.006. S2CID  119438183.
  41. ^ Штойернагель, Оле (2007-08-03). «Эксперимент Афшара не показывает нарушения дополнительности». Основы физики. 37 (9): 1370–1385. arXiv:Quant-ph / 0512123. Bibcode:2007FoPh ... 37.1370S. Дои:10.1007 / s10701-007-9153-5. ISSN  0015-9018. S2CID  53056142.
  42. ^ Жак, В .; Lai, N.D .; Dréau, A .; Zheng, D .; Chauvat, D .; Treussart, F .; Grangier, P .; Роч, Ж.-Ф. (01.01.2008). «Иллюстрация квантовой дополнительности с помощью интерференции одиночных фотонов на решетке». Новый журнал физики. 10 (12): 123009. arXiv:0807.5079. Bibcode:2008NJPh ... 10l3009J. Дои:10.1088/1367-2630/10/12/123009. ISSN  1367-2630. S2CID  2627030.
  43. ^ Георгиев, Данко (26.01.2012). «Квантовые истории и квантовая дополнительность». ISRN Математическая физика. 2012: 1–37. Дои:10.5402/2012/327278.
  44. ^ Дэвид Хэддон. «Восстановление рациональной науки». Оселок. Получено 2007-09-12.
  45. ^ Пол Артур Шилпп, ред, Альберт Эйнштейн: философ-ученый, Открытый суд (1949), ISBN  0-87548-133-7, п. 51.
  46. ^ См. Раздел VI (e) диссертации Эверетта: Теория универсальной волновой функции, в Брайс Селигман ДеВитт, Р. Нил Грэм, ред, Многомировая интерпретация квантовой механики, Принстонская серия по физике, Princeton University Press (1973), ISBN  0-691-08131-XС. 3–140.
  47. ^ Городецкий Р. (1981). «Волна де Бройля и ее двойная волна». Phys. Lett. А. 87 (3): 95–97. Bibcode:1981ФЛА ... 87 ... 95Н. Дои:10.1016/0375-9601(81)90571-5.
  48. ^ Городецкий Р. (1983). «Сверхсветовая сингулярная двойная волна». Lettere al Nuovo Cimento. 38 (15): 509–511. Дои:10.1007 / BF02817964. S2CID  120784358.
  49. ^ Jabs, Артур (2016). «Гипотеза о детерминизме, редукции и измерении в квантовой механике». Квантовые исследования: математика и основы. 3 (4): 279–292. arXiv:1204.0614. Дои:10.1007 / s40509-016-0077-7. S2CID  32523066.
  50. ^ Дуэйн, W. (1923). "Передача в квантах импульса излучения материи". Труды Национальной академии наук Соединенных Штатов Америки. 9 (5): 158–164. Bibcode:1923ПНАС .... 9..158Д. Дои:10.1073 / pnas.9.5.158. ЧВК  1085314. PMID  16576688.
  51. ^ Ланде, А. (1951). Квантовая механика, Сэр Исаак Питман и сыновья, Лондон, стр. 19–22.
  52. ^ Гейзенберг, В. (1930). Физические принципы квантовой теории, переведенный К. Эккартом и Ф. Хойт, Издательство Чикагского университета, Чикаго, стр. 77–78.
  53. ^ Эддингтон, Артур Стэнли (1928). Природа физического мира. Кембридж, Великобритания: MacMillan. стр.201.
  54. ^ Пенроуз, Роджер (2007). Дорога к реальности: полное руководство по законам Вселенной. Винтаж. п.521, §21.10. ISBN  978-0-679-77631-4.
  55. ^ К. Чжэн и Т. Кобаяши, Квантовая оптика как релятивистская теория света; Physics Essays 9 (1996) 447. Годовой отчет, Департамент физики, Школа естественных наук, Токийский университет (1992) 240.
  56. ^ Папагеоргиу, Ник (2 марта 2015 г.). «Пресс-релиз: первая фотография света как частицы и волны». Федеральная политехническая школа Лозанны. Цитировать журнал требует | журнал = (помощь)

внешняя ссылка