Полярон - Polaron

Физика конденсированного состояния
Фазы  · Фаза перехода  · QCP
состояния вещества Твердый  · Жидкость  · Газ  · Плазма  · Конденсат Бозе – Эйнштейна  · Бозе-газ  · Фермионный конденсат  · Ферми газ  · Ферми жидкость  · Сверхтвердый  · Сверхтекучесть  · Жидкость Латтинжера  · Кристалл времени
Фазовые явления Параметр заказа  · Фаза перехода  · QCP
Электронные фазы Электронная зонная структура  · Плазма  · Изолятор  · Изолятор Мотта  · Полупроводник  · Полуметалл  · Дирижер  · Сверхпроводник  · Термоэлектрический  · Пьезоэлектрический  · Сегнетоэлектрик  · Топологический изолятор  · Спиновый бесщелевой полупроводник
Электронные явления Квантовый эффект Холла  · Эффект спин-холла  · Кондо эффект
Магнитные фазы Диамагнетик  · Супердиамагнетик Парамагнетик  · Суперпарамагнетик Ферромагнетик  · Антиферромагнетик Метамагнетик  · Спин-стакан
Квазичастицы Фонон  · Экситон  · Плазмон Поляритон  · Полярон  · Магнон
Мягкая материя Аморфное твердое тело  · Коллоидный  · Гранулированный материал  · Жидкокристаллический  · Полимер
Ученые Ван дер Ваальс  · Оннес  · фон Лауэ  · Брэгг  · Дебай  · Блох  · Онсагер  · Мотт  · Пайерлс  · Ландо  · Латтинджер  · Андерсон  · Ван Влек  · Хаббард  · Шокли  · Бардин  · Купер  · Шриффер  · Джозефсон  · Луи Неэль  · Esaki  · Giaever  · Кон  · Каданов  · Фишер  · Уилсон  · фон Клитцинг  · Binnig  · Рорер  · Беднорз  · Мюллер  · Лафлин  · Störmer  · Ян  · Цуй  · Абрикосов  · Гинзбург  · Леггетт

А полярон это квазичастица используется в физика конденсированного состояния чтобы понять взаимодействие между электроны и атомы в прочном материале. Концепция полярона была впервые предложена Лев Ландау в 1933 году для описания движения электрона в диэлектрик кристалл где атомы перемещаются из положения равновесия, чтобы эффективно экранировать заряд электрона, известный как фонон облако. Это снижает подвижность электронов и увеличивает электронное эффективная масса.

Общая концепция полярона была расширена для описания других взаимодействий между электронами и ионами в металлах, которые приводят к связанное состояние, или снижение энергии по сравнению с невзаимодействующей системой. Основная теоретическая работа была сосредоточена на решении Fröhlich и голштинская Гамильтонианы. Это все еще активная область исследований по поиску точных численных решений для случая одного или двух электронов в большом кристаллическая решетка, и изучить случай многих взаимодействующих электронов.

Экспериментально поляроны важны для понимания самых разных материалов. Подвижность электронов в полупроводники можно сильно уменьшить за счет образования поляронов. Органические полупроводники также чувствительны к поляронным эффектам, что особенно актуально при проектировании органические солнечные батареи что эффективно переносит заряд. Поляроны также важны для интерпретации оптическая проводимость этих типов материалов.

Полярон, а фермионный квазичастица, не следует путать с поляритон, а бозонный квазичастица аналогично гибридизированному состоянию между фотоном и оптическим фононом.

Теория полярона

Энергетический спектр электрона, движущегося в периодическом потенциале жесткого кристаллическая решетка называется Блоховский спектр, который состоит из разрешенных и запрещенных зон. Электрон с энергией внутри разрешенной зоны движется как свободный электрон, но имеет эффективная масса которая отличается от массы электрона в вакууме. Однако кристаллическая решетка деформируема, и смещения атомов (ионов) из их положений равновесия описываются в терминах фононы. Электроны взаимодействуют с этими смещениями, и это взаимодействие известно как электрон-фононная связь. Один из возможных сценариев был предложен в основополагающей статье 1933 г. Лев Ландау, который включает образование дефекта решетки, такого как F-центр и захват электрона этим дефектом. Другой сценарий был предложен Соломон Пекар это предполагает наложение на электрон поляризации решетки (облако виртуальных полярных фононов). Такой электрон с сопутствующей деформацией свободно движется по кристаллу, но с увеличенной эффективной массой.^[1] Пекар придумал для этого носителя заряда термин полярон.

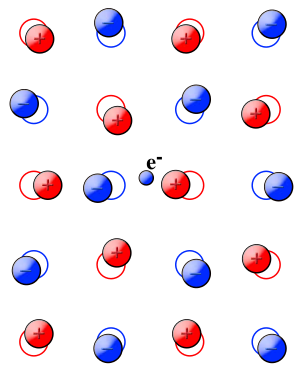
Ландо^[2] и Пекар^[3] легли в основу теории поляронов. Заряд, помещенный в поляризуемую среду, будет экранирован. Диэлектрик Теория описывает явление индукцией поляризации вокруг носителя заряда. Индуцированная поляризация будет следовать за носителем заряда, когда он движется через среду. Носитель вместе с наведенной поляризацией рассматривается как единое целое, называемое поляроном (см. Рис. 1).

Хотя теория поляронов изначально была разработана для электронов как одетых зарядов в кристаллическом поле, нет никаких фундаментальных оснований против любой другой заряженной частицы, которая могла бы взаимодействовать с фононами. Следовательно, и другие заряженные частицы, такие как (электронные) дырки и ионы, должны в целом следовать теории поляронов. Например, протонный полярон был идентифицирован экспериментально в 2017 г.^[4] и на керамических электролитах после гипотезы^[5] о его существовании.

Рис. 1: Художественный взгляд на полярон.^[6] Электрон проводимости в ионном кристалле или полярном полупроводнике отталкивает отрицательные ионы и притягивает положительные ионы. Возникает самоиндуцированный потенциал, который действует на электрон и изменяет его физические свойства.

Обычно в ковалентных полупроводниках связь электронов с деформацией решетки является слабой и образование поляронов не происходит. В полярных полупроводниках электростатическое взаимодействие с индуцированной поляризацией является сильным, и поляроны образуются при низкой температуре, при условии, что концентрация поляронов невелика и экранирование неэффективно. Другой класс материалов, в которых наблюдаются поляроны, - это молекулярные кристаллы, где взаимодействие с молекулярными колебаниями может быть сильным. В случае полярных полупроводников взаимодействие с полярными фононами описывается гамильтонианом Фрелиха. С другой стороны, взаимодействие электронов с молекулярными фононами описывается гамильтонианом Холстейна. Обычно модели, описывающие поляроны, можно разделить на два класса. Первый класс представляет собой модели континуума, в которых не учитывается дискретность кристаллической решетки. В этом случае поляроны связаны слабо или сильно в зависимости от того, мала ли энергия связи полярона по сравнению с частотой фонона. Второй класс обычно рассматриваемых систем - это решеточные модели поляронов. В этом случае поляроны могут быть малыми или большими, в зависимости от соотношения радиуса полярона и постоянной решетки. а.

Электрон проводимости в ионном кристалле или полярном полупроводнике является прототипом полярона. Герберт Фрёлих предложил модель Гамильтониан для этого полярона, через который его динамика рассматривается квантово-механически (гамильтониан Фрёлиха).^[8][9]Сила электрон-фононного взаимодействия определяется безразмерной константой связи ${ Displaystyle альфа = (е ^ {2} / каппа) (м / 2 hbar ^ {3} omega) ^ {1/2}}$. Вот ${ displaystyle m}$ - масса электрона, ${ displaystyle omega}$ - частота фонона и ${ displaystyle kappa ^ {- 1} = { epsilon} _ { infty} ^ {- 1} - { epsilon} _ {0} ^ {- 1}}$, ${ displaystyle { epsilon} _ {0}}$, ${ displaystyle { epsilon} _ { infty}}$ - статическая и высокочастотная диэлектрические проницаемости. В таблице 1 константа связи Фрелиха дана для нескольких твердых тел. Гамильтониан Фрёлиха для одиночного электрона в кристалле с использованием второе квантование обозначение:

${ displaystyle H = H_ {e} + H_ {ph} + H_ {e-ph}}$

${ displaystyle H_ {e} = sum _ {k, s} xi (k, s) c_ {k, s} ^ { dagger} c_ {k, s}}$

${ displaystyle H_ {ph} = sum _ {q, v} omega _ {q, v} a_ {q, v} ^ { dagger} a_ {q, v}}$

${ displaystyle H_ {e-ph} = { frac {1} { sqrt {2N}}} sum _ {k, s, q, v} gamma ( alpha, q, k, v) omega _ {qv} (c_ {k, s} ^ { dagger} c_ {kq, s} a_ {q, v} + c_ {kq, s} ^ { dagger} c_ {k, s} a_ {q, v} ^ { dagger})}$

Точная форма γ зависит от материала и типа фонона, используемого в модели. В случае однополярного режима ${ displaystyle gamma (q) = я hbar omega ({ frac {4 pi alpha} {V_ {0}}} ({ frac { hbar} {m omega}}) ^ {1 / 2}) ^ {1/2} { frac {1} {q}}}$, Вот ${ displaystyle V_ {0}}$ - объем элементарной ячейки. В случае молекулярного кристалла γ обычно не зависит от импульса. Подробное расширенное обсуждение вариаций гамильтониана Фрелиха можно найти в J. T. Devreese и A. S. Alexandrov.^[10] Термины полярон Фрелиха и большой полярон иногда используются как синонимы, поскольку гамильтониан Фрелиха включает приближение континуума и дальнодействующие силы. Нет известного точного решения для гамильтониана Фрелиха с продольным оптическим (LO) фононы и линейный ${ displaystyle gamma}$ (наиболее часто рассматриваемый вариант полярона Фрёлиха), несмотря на обширные исследования.^{[3][7][8][9][11][12][13][14][15][16]}

Несмотря на отсутствие точного решения, известны некоторые приближения свойств полярона.

Физические свойства полярона отличаются от свойств зонного носителя. Полярон характеризуется своим собственная энергия ${ displaystyle Delta E}$, эффективная масса ${ displaystyle m ^ {*}}$ и по своей характеристике ответ к внешним электрическим и магнитным полям (например, подвижность постоянного тока и коэффициент оптического поглощения).

Когда связь слабая (${ displaystyle alpha}$ small), собственная энергия полярона может быть аппроксимирована следующим образом:^[17]

${ displaystyle { frac { Delta E} { hbar omega}} приблизительно - alpha -0.015919622 alpha ^ {2}, qquad qquad qquad (1) ,}$

и масса полярона ${ displaystyle m *}$, которая может быть измерена экспериментами по циклотронному резонансу, больше, чем масса полосы ${ displaystyle m}$ носителя заряда без самоиндуцированной поляризации:^[18]

${ displaystyle { frac {m ^ {*}} {m}} приблизительно 1 + { frac { alpha} {6}} + 0,0236 alpha ^ {2}. qquad qquad qquad (2) }$

Когда связь сильная (α большое), вариационный подход Ландау и Пекара показывает, что собственная энергия пропорциональна α², а масса полярона масштабируется как α⁴. Вариационный расчет Ландау – Пекара.^[3]дает оценку сверху собственной энергии полярона ${ displaystyle E <-C_ {PL} alpha ^ {2}}$, Годен до все α, где ${ displaystyle C_ {PL}}$ постоянная, определяемая путем решения интегро-дифференциальное уравнение. В течение многих лет оставался открытым вопрос, является ли это выражение асимптотически точным при стремлении α к бесконечности. Наконец, Донскер и Варадхан,^[19] применение теория больших отклонений к формулировке интеграла по траекториям Фейнмана для собственной энергии, показал большую точность α этой формулы Ландау – Пекара. Позже Либ и Томас^[20] дал более короткое доказательство с использованием более традиционных методов и с явными оценками поправок нижнего порядка к формуле Ландау – Пекара.

Фейнман^[21] представил вариационный принцип для интегралов по путям для изучения полярона. Он смоделировал взаимодействие между электроном и модами поляризации гармоническим взаимодействием между гипотетической частицей и электроном. Анализ точно решаемой («симметричной») 1D-поляронной модели.^[22][23] Схемы Монте-Карло^[24][25] и другие числовые схемы^[26] демонстрируют замечательную точность подхода Фейнмана к анализу энергии основного состояния полярона. Впоследствии были исследованы более доступные экспериментально свойства полярона, такие как его подвижность и оптическое поглощение.

В пределе сильной связи ${ displaystyle alpha gg 1}$спектр возбужденных состояний полярона начинается с полярон-фононных связанных состояний с энергиями меньше ${ displaystyle hbar omega _ {0}}$, где ${ displaystyle omega _ {0}}$ - частота оптических фононов.^[27]

В решеточных моделях основным параметром является энергия связи полярона: ${ displaystyle E_ {p} = { frac {1} {2N}} sum _ {q} | gamma (q) | ^ {2} / hbar omega}$, ^[28] здесь суммирование ведется по зоне Бриллюэна. Отметим, что эта энергия связи является чисто адиабатической, т.е. не зависит от масс ионов. Для полярных кристаллов величина энергии связи полярона строго определяется диэлектрической проницаемостью ${ displaystyle epsilon _ {0}}$,${ displaystyle epsilon _ { infty}}$, и составляет порядка 0,3-0,8 эВ. Если энергия связи полярона ${ displaystyle E_ {p}}$ меньше интеграла перескока т большой полярон образуется при каком-либо типе электрон-фононного взаимодействия. В случае, когда ${ displaystyle E_ {p}> t}$ образуется малый полярон. В решеточной теории полярона есть два предельных случая. В физически важном адиабатическом пределе ${ displaystyle т gg hbar omega}$ все члены, связанные с ионными массами, сокращены, и образование полярона описывается нелинейным уравнением Шредингера с неадиабатической поправкой, описывающей перенормировку фононной частоты и туннелирование полярона.^[16][29][30] В обратном пределе ${ displaystyle t ll hbar omega}$ теория представляет собой расширение в ${ displaystyle т / hbar omega}$.^[16]

Оптическое поглощение полярон

Выражение для магнитооптического поглощения полярона:^[31]

${ displaystyle Gamma ( Omega) propto - { frac { operatorname {Im} Sigma ( Omega)} { left [ Omega - omega _ { mathrm {c}} - operatorname {Re } Sigma ( Omega) right] ^ {2} + left [ operatorname {Im} Sigma ( Omega) right] ^ {2}}}. Qquad qquad qquad (3)}$

Вот, ${ displaystyle omega _ {c}}$ это циклотронная частота для жесткозонного электрона. Магнитооптическое поглощение Γ (Ω) на частоте Ω принимает вид Σ (Ω) - так называемая «функция памяти», описывающая динамику полярона. Σ (Ω) зависит также от α, β^{[требуется разъяснение ]} и ${ displaystyle omega _ {c}}$.

В отсутствие внешнего магнитного поля (${ displaystyle omega _ {c} = 0}$) спектр оптического поглощения (3) полярона при слабой связи определяется поглощением энергии излучения, которое переизлучается в виде LO-фононов. При большем сцеплении ${ displaystyle alpha geq 5.9}$полярон может переходить в относительно стабильное внутреннее возбужденное состояние, называемое «релаксированным возбужденным состоянием» (RES) (см. рис. 2). Пик RES в спектре также имеет фононную боковую полосу, которая связана с переходом типа Франка – Кондона.

Рис 2. Оптическое поглощение полярона при ${ Displaystyle альфа = 5}$ 6. Пик RES очень интенсивен по сравнению с пиком Франка – Кондона (FC).^[13][32]

Сравнение результатов DSG ^[32] с оптическая проводимость спектры, полученные с помощью бесконтактных численных ^[33] и приблизительные аналитические подходы приведены в ссылке.^[34]

Расчеты оптическая проводимость для полярона Фрёлиха, выполненного в рамках метода диаграммного квантового Монте-Карло,^[33] см. рис. 3, полностью подтверждают результаты вариационного подхода с интегралом по путям^[32] в ${ displaystyle alpha lesssim 3.}$ В режиме промежуточной связи ${ Displaystyle 3 < альфа <6,}$ низкоэнергетическое поведение и положение максимума оптическая проводимость спектр исх.^[33] хорошо следуйте предсказанию Девриза.^[32] Существуют следующие качественные различия между двумя подходами в режиме промежуточной и сильной связи: в работе^[33] доминирующий пик уширяется, а второй пик не развивается, вместо этого возникает плоское плечо в оптическая проводимость спектр на ${ displaystyle alpha = 6}$. Такое поведение можно объяснить оптическими процессами с участием двух^[35] или более фононов. Природа возбужденных состояний полярона требует дальнейшего изучения.

Рис. 3: Спектры оптической проводимости, рассчитанные с использованием метода Диаграммного квантового Монте-Карло (светлые кружки) по сравнению с расчетами DSG (сплошные линии).^[32][33]

Приложение достаточно сильного внешнего магнитного поля позволяет выполнить условие резонанса ${ displaystyle Omega = omega _ { mathrm {c}} + operatorname {Re} Sigma ( Omega)}$, который {(для ${ displaystyle omega _ {c} < omega}$)} определяет частоту поляронного циклотронного резонанса. Из этого условия также может быть получена циклотронная масса полярона. Использование наиболее точных теоретических моделей поляронов для оценки ${ Displaystyle Sigma ( Omega)}$, экспериментальные циклотронные данные хорошо объясняются.

Доказательства поляронного характера носителей заряда в AgBr и AgCl были получены с помощью высокоточных экспериментов по циклотронному резонансу во внешних магнитных полях до 16 Тл.^[36] Магнитопоглощение полной связи, рассчитанное в работе^[31] приводит к наилучшему количественному согласию теории и эксперимента для AgBr и AgCl. Эта количественная интерпретация эксперимента циклотронного резонанса в AgBr и AgCl^[36] по теории Петерса^[31] предоставил одну из наиболее убедительных и ярких демонстраций поляронных свойств Фрелиха в твердых телах.

Экспериментальные данные по магнитополяронному эффекту, полученные с использованием методов фотопроводимости в дальней инфракрасной области, были применены для исследования энергетического спектра мелких доноров в полярных полупроводниковых слоях CdTe.^[37]

Поляронный эффект, значительно превышающий энергию фононов LO, изучался с помощью измерений циклотронного резонанса, например. ж., в полупроводниках AIIBVI, наблюдаемых в сверхсильных магнитных полях.^[38] Резонансный поляронный эффект проявляется, когда циклотронная частота приближается к энергии LO-фонона в достаточно сильных магнитных полях.

В решетчатых моделях оптическая проводимость определяется формулой:^[28]

${ displaystyle sigma ( Omega) = n_ {p} e ^ {2} a ^ {2} ({ frac { pi ^ { frac {1} {2}} t ^ {2} (1- e ^ { frac { hbar Omega} {k_ {B} T}})} {2 hbar ^ {2} Omega (E_ {a} k_ {B} T) ^ {1/2}}} ) exp (- { frac {( hbar Omega -4E_ {a}) ^ {2}} {16E_ {a} k_ {B} T}})}$

Вот ${ displaystyle E_ {a}}$ - энергия активации полярона порядка энергии связи полярона ${ displaystyle E_ {p}}$. Эта формула была получена и подробно обсуждалась в^[39][40][41] и был испытан экспериментально, например, на фотодопированных исходных соединениях высокотемпературных сверхпроводников.^[42]

Поляроны в двух измерениях и в квазидвумерных структурах

Большой интерес к изучению двумерного электронного газа (2DEG) также привел к многочисленным исследованиям свойств поляронов в двух измерениях.^[43][44][45] Простая модель 2D-поляронной системы состоит из электрона, удерживаемого в плоскости, который взаимодействует посредством взаимодействия Фрелиха с LO-фононами окружающей 3D-среды. Собственная энергия и масса такого 2D полярона больше не описываются выражениями, действительными в 3D; для слабой связи они могут быть аппроксимированы как:^[46][47]

${ displaystyle { frac { Delta E} { hbar omega}} приблизительно - { frac { pi} {2}} alpha -0.06397 alpha ^ {2}; qquad qquad qquad (4) ,}$

${ displaystyle { frac {m ^ {*}} {m}} приблизительно 1 + { frac { pi} {8}} alpha +0.1272348 alpha ^ {2}. qquad qquad qquad (5) ,}$

Было показано, что существуют простые масштабные соотношения, связывающие физические свойства поляронов в 2D и в 3D. Пример такого масштабного отношения:^[45]

${ displaystyle { frac {m_ {2D} ^ {*} ( alpha)} {m_ {2D}}} = { frac {m_ {3D} ^ {*} ({ frac {3} {4}) } pi alpha)} {m_ {3D}}}, qquad qquad qquad (6) ,}$

где ${ Displaystyle м _ { mathrm {2D}} ^ {*}}$ (${ Displaystyle м _ { mathrm {3D}} ^ {*}}$) и ${ displaystyle m _ { mathrm {2D}}}$ (${ displaystyle m _ { mathrm {3D}}}$) - соответственно массы полярона и электронной зоны в 2D (3D).

Эффект удержания полярона Фрёлиха заключается в усилении эффективный поляронная связь. Однако эффекты многих частиц, как правило, уравновешивают этот эффект из-за экранирования.^[43][48]

Также в 2D-системах циклотронный резонанс удобный инструмент для изучения поляронных эффектов. Хотя необходимо учитывать несколько других эффектов (непараболичность электронных зон, многотельный эффекты, природа удерживающего потенциала и т. д.) поляронный эффект отчетливо проявляется в циклотронной массе. Интересная 2D-система состоит из электронов на пленках жидкого Не.^[49][50] В этой системе электроны соединяются с рипплонами жидкого гелия, образуя «рипплополяроны». Эффективная связь может быть относительно большой, и при некоторых значениях параметров может произойти самозахват. Акустическая природа дисперсии риплонов на длинных волнах является ключевым аспектом захвата.

Для GaAs / Al_ИксGa_1-хКак квантовые ямы и сверхрешетки, поляронный эффект снижает энергию мелких донорных состояний в слабых магнитных полях и приводит к резонансному расщеплению энергий в сильных магнитных полях. Энергетические спектры таких поляронных систем, как мелкие доноры («связанные поляроны»), e. г., D₀ и D⁻ центры, представляют собой наиболее полную и подробную поляронную спектроскопию из всех известных в литературе.^[51]

В квантовых ямах GaAs / AlAs с достаточно высокой концентрацией электронов антипересечение спектров циклотронного резонанса наблюдалось вблизи частоты поперечного оптического (TO) фонона GaAs, а не вблизи частоты LO-фонона GaAs.^[52] Это антипересечение вблизи частоты ТО-фонона было объяснено в рамках теории поляронов.^[53]

Помимо оптических свойств,^[7][15][54] были изучены многие другие физические свойства поляронов, в том числе возможность автолокализации, поляронный транспорт,^[55] магнитофононный резонанс и др.

Расширения концепции полярона

Значительным является также расширение концепции полярона: акустический полярон, пьезоэлектрический полярон, электронный полярон, связанный полярон, захваченный полярон, вращение полярон, молекулярный полярон, сольватированные поляроны, поляронный экситон, полярон Яна-Теллера, малый полярон, биполяроны и многополяронные системы.^[7] Вызываются эти расширения концепции, например. г., для изучения свойств сопряженных полимеров, перовскитов с колоссальным магнитосопротивлением, высоко-${ displaystyle T_ {c}}$ сверхпроводники, слоистый MgB₂ сверхпроводники, фуллерены, квазиодномерные проводники, полупроводниковые наноструктуры.

Возможность того, что поляроны и биполяроны играют роль в высоких${ displaystyle T_ {c}}$ сверхпроводники возродил интерес к физическим свойствам многополяронных систем и, в частности, к их оптическим свойствам. Теоретические исследования были расширены от однополяронных до многополяронных систем.^[7][56][57]

Новый аспект концепции полярона был исследован для полупроводников. наноструктуры: экситон-фононные состояния не факторизуемы в адиабатический анзац произведения, так что неадиабатический лечение необходимо.^[58] В неадиабатичность экситон-фононных систем приводит к сильному увеличению вероятностей фононно-вспомогательных переходов (по сравнению с адиабатически рассматриваемыми) и к многофононным оптическим спектрам, которые значительно отличаются от Франк-Кондон прогрессирует даже при малых значениях константы электрон-фононного взаимодействия, как в случае типичных полупроводниковых наноструктур.^[58]

В биофизике Давыдовский солитон распространяется по белок α-спираль автолокализованное возбуждение амида I, которое является решением гамильтониана Давыдова. Математические методы, которые используются для анализа солитона Давыдова, аналогичны некоторым, которые были разработаны в теории поляронов. В этом контексте Давыдовский солитон соответствует полярон то есть (я) большой так что приближение континуального предела оправдано, (ii) акустический потому что автолокализация возникает из-за взаимодействия с акустическими модами решетки, и (iii) слабосвязанный потому что ангармоническая энергия мала по сравнению с шириной полосы фононов.^[59]

Было показано, что система примеси в Конденсат Бозе – Эйнштейна также является членом семейства поляронов.^[60] Это позволяет изучить ранее недоступный режим сильной связи, поскольку силы взаимодействия могут быть настроены извне с помощью Резонанс Фешбаха. Это недавно было экспериментально установлено двумя исследовательскими группами.^[61][62]Существование полярона в Конденсат Бозе – Эйнштейна было продемонстрировано как для взаимодействий притяжения, так и для отталкивания, включая режим сильной связи.

Смотрите также

• Экситон
• Сигурд Зиенау
• ТИ-полярон

использованная литература

внешние ссылки