Кварковая модель - Quark model

Рисунок 1: В псевдоскалярный мезон нонет. Члены исходного мезонного «октета» показаны зеленым, синглет - пурпурным. Хотя эти мезоны теперь сгруппированы в нонет, Восьмеричный путь Название происходит от модели восьми для мезонов и барионов в исходной схеме классификации.

В физика элементарных частиц, то кварковая модель это схема классификации для адроны с точки зрения их валентности кварки - кварки и антикварки, дающие начало квантовые числа адронов. Модель кварка лежит в основе "аромат СУ (3)", или Восьмеричный путь, успешная схема классификации, организующая большое количество более легких адроны которые открывались с 1950-х по 1960-е годы. Он получил экспериментальную проверку, начиная с конца 1960-х годов, и на сегодняшний день является действительной эффективной классификацией. Модель была независимо предложена физиками. Мюррей Гелл-Манн,^[1] кто в краткой статье назвал их «кварками», и Джордж Цвейг,^[2]^[3] кто предложил «тузы» в более длинной рукописи. Андре Петерманн также затронули центральные идеи с 1963 по 1965 год, без такого количественного обоснования.^[4]^[5] Сегодня эта модель была по существу поглощена как компонент устоявшейся квантовая теория поля сильных и электрослабых взаимодействий частиц, получивших название Стандартная модель.

Адроны на самом деле не являются «элементарными», и их можно рассматривать как связанные состояния их «валентных кварков» и антикварков, которые приводят к возникновению квантовые числа адронов. Эти квантовые числа представляют собой метки, идентифицирующие адроны, и бывают двух видов. Один комплект поступает из Симметрия Пуанкаре —J^ПК, куда J, п и C стоять за полный угловой момент, P-симметрия, и C-симметрия, соответственно.

Остальные квантовые числа аромата такой как изоспин, странность, очарование, и так далее. Сильные взаимодействия, связывающие кварки вместе, нечувствительны к этим квантовым числам, поэтому их изменение приводит к систематическим отношениям массы и связи между адронами в одном и том же мультиплете аромата.

Всем кваркам присваивается барионное число из ⅓. Вверх, очарование и топ-кварки есть электрический заряд + ⅔, а вниз, странный, и нижние кварки имеют электрический заряд −⅓. Антикварки имеют противоположные квантовые числа. Кварки спин-½ частицы, и таким образом фермионы. Каждый кварк или антикварк подчиняется формуле Гелл-Манна-Нишиджима индивидуально, так что любая их аддитивная сборка тоже будет.

Мезоны состоят из пары валентных кварк-антикварк (таким образом, имеют барионное число 0), а барионы состоят из трех кварков (таким образом, имеют барионное число 1). В этой статье обсуждается кварковая модель для восходящего, нижнего и странного ароматов кварка (которые образуют приблизительный аромат SU (3) симметрия ). Есть обобщения на большее количество вкусов.

История

Разработка схем классификации для адроны стал своевременным вопросом после того, как новые экспериментальные методы обнаружили так много из них, что стало ясно, что не все они могут быть элементарными. Эти открытия привели Вольфганг Паули воскликнуть: «Если бы я предвидел это, я бы занялся ботаникой». и Энрико Ферми посоветовать своему ученику Леон Ледерман: «Молодой человек, если бы я мог вспомнить названия этих частиц, я был бы ботаником». Эти новые схемы принесли Нобелевские премии физикам-экспериментаторам элементарных частиц, в том числе Луис Альварес, который был в авангарде многих из этих разработок. Построение адронов как связанных состояний меньшего числа составляющих, таким образом, организовало бы настоящий «зоопарк». Несколько ранних предложений, например, Энрико Ферми и Чен-Нин Ян (1949), а Модель Саката (1956), в конечном итоге удовлетворительно покрыли мезоны, но потерпели неудачу с барионами, и поэтому не смогли объяснить все данные.

В Формула Гелл-Манна – Нисиджимы, разработан Мюррей Гелл-Манн и Кадзухико Нисидзима, привело к Восьмеричный путь классификации, изобретенной Гелл-Манном, с важным независимым вкладом Юваль Нееман, в 1961 г. Адроны были организованы в мультиплеты, октеты и декуплеты представления SU (3) примерно одинаковой массы из-за сильных взаимодействий; и меньшая разница масс, связанная с квантовыми числами аромата, невидимая для сильных взаимодействий. В Формула масс Гелл-Манна – Окубо систематизировал количественную оценку этих небольших различий масс между членами адронного мультиплета, контролируемого явное нарушение симметрии из SU (3).

Спин-³⁄₂
Ω⁻
барион, член декуплета основного состояния, был решающим предсказанием этой классификации. После того, как это было обнаружено в эксперименте на Брукхейвенская национальная лаборатория, Гелл-Манн получил Нобелевская премия по физике за его работу о Восьмеричном пути в 1969 году.

Наконец, в 1964 году Гелл-Манн и независимо друг от друга Джордж Цвейг, выяснили, что кодирует картина Восьмеричного Пути: они постулировали три элементарных фермионных составляющих - «верхний», «нижний» и «странный» кварки, которые не наблюдаются и, возможно, ненаблюдаемы в свободной форме. Простые попарные или тройные комбинации этих трех составляющих и их античастиц лежат в основе и элегантно кодируют восьмеричную классификацию в экономичной и жесткой структуре, что приводит к дальнейшей простоте. Адронные различия масс теперь были связаны с разными массами составляющих кварков.

Потребуется около десяти лет, чтобы неожиданная природа - и физическая реальность - этих кварков была оценена более полно (см. Кварки ). Как ни странно, их нельзя наблюдать изолированно (ограничение цвета ), но вместо этого всегда объединяются с другими кварками с образованием полных адронов, которые затем предоставляют обширную косвенную информацию о самих захваченных кварках. Наоборот, кварки служат в определении квантовая хромодинамика, фундаментальная теория, полностью описывающая сильные взаимодействия; и теперь понимают, что Восьмеричный Путь является следствием структуры симметрии аромата трех самых легких из них.

Мезоны

Фигура 2: Псевдоскалярный мезоны со спином 0 образуют нонет

Рисунок 3: Мезоны спина 1 образуют нонет

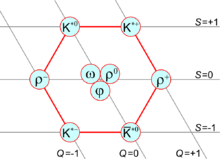
Классификация Восьмеричного Пути названа в честь следующего факта: если мы берем три разновидности кварков, то кварки лежат в фундаментальное представление, 3 (называемый тройкой) вкус SU (3). Антикварки лежат в комплексно сопряженном представлении 3. Девять состояний (nonet), состоящих из пары, можно разложить на тривиальное представление, 1 (называется синглетом), а присоединенное представительство, 8 (называется октетом). Обозначения для этого разложения:

{ Displaystyle mathbf {3} otimes mathbf { overline {3}} = mathbf {8} oplus mathbf {1}}

.

На рисунке 1 показано приложение этого разложения к мезонам. Если бы симметрия аромата была точной (как в пределе, когда действуют только сильные взаимодействия, а электрослабые взаимодействия условно отключены), то все девять мезонов имели бы одинаковую массу. Однако физическое содержание полной теории^{[требуется разъяснение ]} включает рассмотрение нарушения симметрии, вызванного различиями масс кварков, и рассмотрение смешивания между различными мультиплетами (такими как октет и синглет).

N.B. Тем не менее массовое расщепление между
η
и
η ′
больше, чем может вместить кварковая модель, и это "
η
–
η ′
головоломка "происходит из топологических особенностей вакуума сильного взаимодействия, таких как Немедленное включение конфигурации.

Мезоны - это адроны с нулевым барионное число. Если пара кварк – антикварк находится в орбитальный угловой момент $L$ состояние и иметь вращение $S$ , тогда

|L − S| ≤ J ≤ L + S, куда S = 0 или 1,
п = (−1)^{L + 1}, где 1 в экспоненте возникает из-за внутренняя четность пары кварк – антикварк.
C = (−1)^{L + S} для мезонов, у которых нет вкус. Ароматизированные мезоны имеют неопределенное значение C.
За изоспин я = 1 и 0, можно определить новый мультипликативное квантовое число называется G-паритет такой, что грамм = (−1)^{я + L + S}.

Если п = (−1)^J, то следует, что S = 1, поэтому ПК= 1. Состояния с этими квантовыми числами называются государства естественного паритета; а все остальные квантовые числа называются экзотика (например, состояние J^ПК = 0⁻⁻).

Барионы

Рисунок 4. В S = ¹⁄₂ барионный октет основного состояния

Рисунок 5. В S = ³⁄₂ барионный декуплет

Поскольку кварки фермионы, то спин-статистическая теорема означает, что волновая функция бариона должен быть антисимметричным при обмене любыми двумя кварками. Эта антисимметричная волновая функция получается, делая ее полностью антисимметричной по цвету, обсуждаемой ниже, и симметричной по аромату, спину и пространству вместе взятых. С тремя ароматизаторами разложение аромата

{ displaystyle mathbf {3} otimes mathbf {3} otimes mathbf {3} = mathbf {10} _ {S} oplus mathbf {8} _ {M} oplus mathbf {8} _ {M} oplus mathbf {1} _ {A}}

.

Декуплет симметричен по аромату, синглет антисимметричен, а два октета имеют смешанную симметрию. Таким образом, пространственная и спиновая части состояний фиксируются, если задан орбитальный угловой момент.

Иногда полезно подумать о базовые состояния кварков как шесть состояний трех ароматов и двух спинов на аромат. Эта приблизительная симметрия называется спин-флейвором. SU (6). В терминах этого разложение имеет вид

{ displaystyle mathbf {6} otimes mathbf {6} otimes mathbf {6} = mathbf {56} _ {S} oplus mathbf {70} _ {M} oplus mathbf {70} _ {M} oplus mathbf {20} _ {A} ~.}

56 состояний с симметричным сочетанием спина и аромата разлагаются под действием аромата. SU (3) в

{ displaystyle mathbf {56} = mathbf {10} ^ { frac {3} {2}} oplus mathbf {8} ^ { frac {1} {2}} ~,}

где верхний индекс обозначает спин, S, бариона. Поскольку эти состояния симметричны по спину и аромату, они также должны быть симметричными в пространстве - условие, которое легко выполняется, если задать орбитальный угловой момент L = 0. Это барионы основного состояния.

В S = ¹⁄₂ октетные барионы - это два нуклоны (
п⁺
,
п⁰
), три Сигма (
Σ⁺
,
Σ⁰
,
Σ⁻
), два Xis (
Ξ⁰
,
Ξ⁻
), а Лямбда (
Λ⁰
). В S = ³⁄₂ декуплетные барионы четыре Дельты (
Δ⁺⁺
,
Δ⁺
,
Δ⁰
,
Δ⁻
), три Сигма (
Σ^∗+
,
Σ^∗0
,
Σ^∗−
), два Xis (
Ξ^∗0
,
Ξ^∗−
), а Омега (
Ω⁻
).

Например, составляющая модель кварка волновая функция для протона имеет вид

{ displaystyle | p _ { uparrow} rangle = { frac {1} { sqrt {18}}} [2 | u _ { uparrow} d _ { downarrow} u _ { uparrow} rangle +2 | u_ { uparrow} u _ { uparrow} d _ { downarrow} rangle +2 | d _ { downarrow} u _ { uparrow} u _ { uparrow} rangle - | u _ { uparrow} u _ { downarrow} d_ { uparrow} rangle - | u _ { uparrow} d _ { uparrow} u _ { downarrow} rangle - | u _ { downarrow} d _ { uparrow} u _ { uparrow} rangle - | d _ { uparrow} u _ { downarrow} u _ { uparrow} rangle - | d _ { uparrow} u _ { uparrow} u _ { downarrow} rangle - | u _ { downarrow} u _ { uparrow} d _ { uparrow} rangle ].}

Смешивание барионов, расщепление масс внутри мультиплетов и между ними, а также магнитные моменты - вот некоторые из других величин, которые модель успешно предсказывает.

Открытие цвета

Цветные квантовые числа являются характерными зарядами сильного взаимодействия и совершенно не участвуют в электрослабых взаимодействиях. Они были открыты в результате классификации кварковых моделей, когда стало понятно, что спин S = ³⁄₂ барион
Δ⁺⁺
, требовалось три верхних кварка с параллельными спинами и нулевым орбитальным угловым моментом. Следовательно, он не может иметь антисимметричную волновую функцию (требуемую Принцип исключения Паули ), если не было скрытого квантового числа. Оскар Гринберг отметил эту проблему в 1964 году, предположив, что кварки должны быть парафермионы.^[6]

Вместо этого, шесть месяцев спустя, Му-Ён Хан и Ёитиро Намбу предположил существование трех триплетов кварков, чтобы решить эту проблему, но аромат и цвет переплелись в этой модели: они не коммутируются.^[7]

Современная концепция цвета, полностью сочетающегося со всеми остальными зарядами и обеспечивающего сильный силовой заряд, была сформулирована в 1973 г. Уильям Бардин, Харальд Фрич,и Мюррей Гелл-Манн.^[8]^[9]

Состояния вне кварковой модели

В то время как кварковая модель выводится из теории квантовая хромодинамика, структура адронов сложнее, чем позволяет эта модель. Полный квантово-механический волновая функция любого адрона должны включать виртуальные кварковые пары, а также виртуальные глюоны, и позволяет использовать самые разные смеси. Могут быть адроны, лежащие вне кварковой модели. Среди них глюболы (которые содержат только валентные глюоны), гибриды (которые содержат валентные кварки, а также глюоны) и "экзотические адроны " (Такие как тетракварки или же пентакварки ).

Смотрите также

Примечания

^ Гелл-Манн, М. (4 января 1964 г.). «Схематическая модель барионов и мезонов». Письма по физике. 8 (3): 214–215. Bibcode:1964ФЛ ..... 8..214Г. Дои:10.1016 / S0031-9163 (64) 92001-3.
^ Цвейг, Г. (17 января 1964 г.). Модель SU (3) симметрии сильного взаимодействия и ее нарушение (PDF) (Отчет). Отчет ЦЕРН № 8182 / TH.401.
^ Цвейг, Г. (1964). Модель SU (3) для симметрии сильного взаимодействия и ее нарушения: II (PDF) (Отчет). Отчет ЦЕРН № 8419 / TH.412.
^ Петерманн, А. (1965). "Свойства странности и формула массы для векторных мезонов" [Свойства странности и массовая формула для векторного мезона]. Ядерная физика. 63 (2): 349–352. arXiv:1412.8681. Bibcode:1965NucPh..63..349P. Дои:10.1016/0029-5582(65)90348-2.
^ Петров Владимир Александрович (23–27 июня 2014 г.). Полвека с КВАРКАМИ. XXX-й Международный семинар по физике высоких энергий. Протвино, Московская область, Россия. arXiv:1412.8681.
^ Гринберг, О. (1964). «Спиновая и унитарно-спиновая независимость в паракварковой модели барионов и мезонов». Письма с физическими проверками. 13 (20): 598–602. Bibcode:1964ПхРвЛ..13..598Г. Дои:10.1103 / PhysRevLett.13.598.
^ Han, M.Y .; Намбу, Ю. (1965). «Трехтриплетная модель с двойной SU (3) симметрией». Физический обзор B. 139 (4В): 1006. Bibcode:1965ПхРв..139.1006Г. Дои:10.1103 / PhysRev.139.B1006.
^ Bardeen, W .; Fritzsch, H .; Гелл-Манн, М. (1973). "Алгебра токов светового конуса, π⁰ распад, и е⁺ е⁻ аннигиляция ". В Гатто, Р. (ред.). Масштаб и конформная симметрия в физике адронов. Джон Уайли и сыновья. п.139. arXiv:hep-ph / 0211388. Bibcode:2002hep.ph ... 11388B. ISBN 0-471-29292-3.
^ Fritzsch, H .; Gell-Mann, M .; Leutwyler, H. (1973). «Преимущества цветного октетно-глюонного изображения». Письма по физике B. 47 (4): 365. Bibcode:1973ФЛБ ... 47..365Ф. CiteSeerX 10.1.1.453.4712. Дои:10.1016/0370-2693(73)90625-4.