Аньон - Anyon

Статистическая механика
Термодинамика Кинетическая теория
Статистика частиц Теорема спин-статистики Идентичные частицы Максвелл – Больцманн Бозе-Эйнштейн Ферми – Дирак Парастатистика Статистика Anyonic Статистика косы
Термодинамические ансамбли NVE Микроканонический NVT Канонический мкВт Большой канонический НПХ Изоэнтальпийно-изобарический ДНЯО Изотермически-изобарический
Модели Дебай Эйнштейн Я пою Potts
Потенциал Внутренняя энергия Энтальпия Свободная энергия Гельмгольца Свободная энергия Гиббса Большой потенциал / свободная энергия Ландау
Ученые Максвелл Больцман Гиббс Эйнштейн Эренфест фон Нейман Толман Дебай Ферми Bose

В физика, анйон это тип квазичастица это происходит только в два-размерный системы, со свойствами гораздо менее ограниченными, чем фермионы и бозоны. В общем, эксплуатация обмен двух одинаковых частиц может вызвать глобальный фазовый сдвиг, но не может повлиять наблюдаемые. Anyons обычно классифицируются как абелевский или неабелев. Обнаружены абелевы эйоны^[1] и играть важную роль в дробный квантовый эффект Холла. Неабелевы анионы окончательно не обнаружены, хотя это активная область исследований.

Введение

В статистическая механика больших систем многих тел подчиняются законам, описываемым Статистика Максвелла-Больцмана. Квантовая статистика более сложен из-за различного поведения двух разных типов частиц, называемых фермионы и бозоны. Цитируя недавнее простое описание из Университет Аалто:^[2]

В трехмерном мире, в котором мы живем, есть только два типа частиц: «фермионы», которые отталкиваются друг от друга, и «бозоны», которые любят слипаться. Общеизвестный фермион - электрон, переносящий электричество; а широко известный бозон - это фотон, несущий свет. Однако в двумерном мире существует другой тип частиц, анион, который не ведет себя как фермион или бозон.

В двумерном мире два идентичных эниона меняют свою волновую функцию, когда они меняются местами способами, которые невозможны в трехмерной физике:^[3]

... в двух измерениях дважды обмен идентичными частицами не равносилен оставлению их в покое. Волновая функция частиц после двукратной перестановки местами может отличаться от исходной; частицы с такой необычной статистикой обмена известны как энионы. Напротив, в трех измерениях дважды обменивающиеся частицы не могут изменить их волновую функцию, оставляя нам только две возможности: бозоны, волновая функция которых остается неизменной даже после однократного обмена, и фермионы, обмен которых меняет только знак их волновой функции.

Этот процесс обмена идентичными частицами или вращения одной частицы вокруг другой называется математическим названием "плетение. »« Сплетение »двух энионов создает историческую запись события, поскольку их измененные волновые функции« подсчитывают »количество кос.^[4]

Microsoft инвестировал в исследования, касающиеся анионов, как потенциальную основу для топологические квантовые вычисления. Любые люди, окружающие друг друга ("плетение"), будут кодировать информацию более надежным способом, чем другие потенциальные квантовые вычисления технологии.^[5] Однако большая часть инвестиций в квантовые вычисления основана на методах, которые не используют никого.^[5]

Абелевы аньоны

В квантовой механике и некоторых классических стохастических системах неразличимые частицы обладают тем свойством, что обмениваются состояниями частицыя с частицейj (символически ${ displaystyle psi _ {i} leftrightarrow psi _ {j} { text {for}} i neq j}$) не приводит к ощутимо иному многотельному состоянию.

В квантово-механической системе, например, система с двумя неразличимыми частицами, причем частица 1 находится в состоянии ${ displaystyle psi _ {1}}$ и частица 2 в состоянии ${ displaystyle psi _ {2}}$, имеет состояние ${ displaystyle left | psi _ {1} psi _ {2} right rangle}$ в Обозначение Дирака. Теперь предположим, что мы обмениваемся состояниями двух частиц, тогда состояние системы будет ${ displaystyle left | psi _ {2} psi _ {1} right rangle}$. Эти два состояния не должны иметь измеримую разницу, поэтому они должны быть одним и тем же вектором с точностью до фазовый фактор:

${ Displaystyle left | psi _ {1} psi _ {2} right rangle = e ^ {i theta} left | psi _ {2} psi _ {1} right rangle. }$

В пространстве три или более измерений, элементарные частицы являются либо фермионами, либо бозонами, в зависимости от их статистическое поведение. Фермионы подчиняются Статистика Ферми – Дирака, а бозоны подчиняются Статистика Бозе – Эйнштейна. Для бозонов фазовый фактор равен ${ displaystyle 1}$, а для фермионов - ${ displaystyle -1}$. В частности, поэтому фермионы подчиняются Принцип исключения Паули: Если два фермиона находятся в одном состоянии, то имеем

${ Displaystyle left | psi psi right rangle = - left | psi psi right rangle.}$

Вектор состояния должен быть нулевым, что означает, что он не нормализуемый, а значит нефизический.

Однако в двумерных системах квазичастицы можно наблюдать, что подчиняются статистике в непрерывном диапазоне между статистикой Ферми – Дирака и Бозе – Эйнштейна, как было впервые показано Джон Магне Лейнаас и Ян Мирхейм из Университет Осло в 1977 г.^[6] В случае двух частиц это можно выразить как

${ Displaystyle left | psi _ {1} psi _ {2} right rangle = e ^ {i theta} left | psi _ {2} psi _ {1} right rangle, }$

где ${ Displaystyle е ^ {я тета}}$ могут быть другие значения, кроме просто ${ displaystyle -1}$ или ${ displaystyle 1}$. Важно отметить, что существует небольшая злоупотребление обозначениями в этом сокращенном выражении, поскольку в действительности эта волновая функция может быть и обычно является многозначной. Это выражение фактически означает, что когда частица 1 и частица 2 меняются местами в процессе, когда каждая из них совершает половину оборота против часовой стрелки относительно другой, двухчастичная система возвращается к своей исходной квантовой волновой функции, за исключением умножения на комплексную единичную норму. фазовый фактор е^iθ. И наоборот, при повороте на половину оборота по часовой стрелке волновая функция умножается на е^−iθ. Такая теория, очевидно, имеет смысл только в двух измерениях, где по часовой стрелке и против часовой стрелки четко определены направления.

В этом случае θ = π восстанавливаем статистику Ферми – Дирака (е^я = −1) и в случае θ = 0 (или θ = 2π) статистика Бозе – Эйнштейна (е^2πi = 1). Между ними есть кое-что другое. Франк Вильчек в 1982 году исследовал поведение таких квазичастиц и придумал термин «энион» для их описания, потому что они могут иметь любую фазу, когда частицы меняются местами.^[7] В отличие от бозонов и фермионов, анионы обладают тем особенным свойством, что, когда они дважды меняются местами одним и тем же способом (например, если Anyon 1 и Anyon 2 вращались против часовой стрелки на пол-оборота друг относительно друга, чтобы поменяться местами, а затем они вращались против часовой стрелки на пол-оборота) друг относительно друга снова, чтобы вернуться на свои исходные места), волновая функция не обязательно одинакова, а, скорее, обычно умножается на некоторую сложную фазу (на е^2iθ в этом примере).

Мы также можем использовать θ = 2π s с частицей вращение квантовое число s, с участием s будучи целое число для бозонов, полуцелое число для фермионов, так что

${ Displaystyle е ^ {я тета} = е ^ {2i pi s} = (- 1) ^ {2s},}$ или ${ Displaystyle left | psi _ {1} psi _ {2} right rangle = (- 1) ^ {2s} left | psi _ {2} psi _ {1} right rangle .}$

На краю, дробный квантовый эффект Холла Энионы ограничены перемещением в одном пространственном измерении. Математические модели одномерных энионов составляют основу приведенных выше коммутационных соотношений.

В трехмерном позиционном пространстве операторы статистики фермионов и бозонов (−1 и +1 соответственно) являются всего лишь одномерными представлениями группа перестановок (S_N из N неразличимые частицы), действующие на пространство волновых функций. Таким же образом в двумерном позиционном пространстве операторы абелевой анионной статистики (е^iθ) являются всего лишь одномерными представлениями группа кос (B_N из N неразличимые частицы), действующие на пространство волновых функций. Неабелевы энионные статистики - многомерные представления группы кос. Статистику Anyonic не следует путать с парастатистика, который описывает статистику частиц, волновые функции которых являются многомерными представлениями группы перестановок.^[8]:22

Топологическая эквивалентность

Тот факт, что гомотопические классы путей (т.е. понятие эквивалентность на косы ) являются уместными намеками на более тонкое понимание. Это возникает из Интеграл по путям Фейнмана, в котором все пути от начальной до конечной точки в пространство-время внести свой вклад в соответствующий фазовый фактор. Напомним, что Интеграл по путям Фейнмана может быть мотивирован расширением пропагатора с помощью метода, называемого квантованием времени,^[9] в котором время дискретизировано.

В негомотопических путях нельзя попасть из любой точки в одном временном срезе в любую другую точку в следующем временном срезе. Это означает, что мы можем рассматривать гомотопный Класс эквивалентности путей для различных весовых коэффициентов.^[10]

Итак, видно, что топологический понятие эквивалентности пришло из исследования Интеграл по путям Фейнмана.^[8]:28

Для более прозрачного способа увидеть, что гомотопическое понятие эквивалентности является «правильным» для использования, см. Эффект Ааронова – Бома.

Эксперимент

Группа физики-теоретики работая в Университет Осло во главе с Джон Лейнаас и Ян Мирхейм, рассчитанный в 1977 году, что традиционное разделение на фермионы и бозоны не применимо к теоретическим частицам, существующим в двух Габаритные размеры.^[11] Ожидается, что такие частицы будут проявлять широкий диапазон ранее неожиданных свойств. В 1982 году Фрэнк Вильчек опубликовал две статьи, исследуя дробную статистику квазичастиц в двух измерениях, дав им название «энионы».^[12]

Лафлин квазичастичный интерферометр растровая электронная микрофотография из полупроводниковый прибор. Четыре светло-серых области Au /Ti ворота ООНистощенный электроны; синие кривые - это краевые каналы от эквипотенциальные возможности этих необеспеченных электронов. Темно-серые кривые - вытравленные канавки, обедненные электронами, синие точки - туннельные переходы, желтые точки Омические контакты. Электроны в устройстве удерживаются в плоскости 2d.^[13]

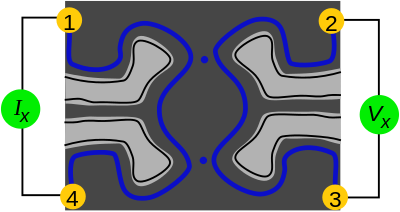
Даниэль Цуй и Хорст Штёрмер открыл дробный квантовый эффект Холла в 1982 году. Математика, разработанная Вильчеком, оказалась полезной для Бертран Гальперин в Гарвардский университет в объяснении его аспектов.^[14] Фрэнк Вильчек, Дэн Аровас и Роберт Шриффер подтвердил это утверждение в 1985 году с помощью явного вычисления, предсказывающего, что частицы, существующие в этих системах, на самом деле являются анионами.^[15]

В 2020 году Х. Бартоломей и соавторы из École normale supérieure (Париж) из эксперимента в двумерной гетероструктуре GaAs / AlGaAs была определена промежуточная энионная статистика ${ displaystyle theta = { frac { pi} {3}}}$ путем электрических корреляционных измерений токов через третий контакт при столкновениях энионов в электронном газе от двухточечных контактов.^[16]

С развитием в полупроводник технология, означающая, что возможно нанесение тонких двумерных слоев - например, в листах графен - исследуется долгосрочный потенциал использования свойств анионов в электронике.

В 2020 году группа ученых из Университета Пердью объявила о новых экспериментальных доказательствах существования энионов. Интерферометр команды направляет электроны через специфическую травленую наноструктуру, похожую на лабиринт, сделанную из арсенида галлия и арсенида алюминия-галлия. «В случае наших анионов фаза, генерируемая плетением, была 2π / 3», - сказал он. «Это отличается от того, что видели в природе раньше».^[17][18]

Неабелевы энионы

Нерешенная проблема в физике: Является топологический порядок стабильно на ненулевом уровне температура ? (больше нерешенных задач по физике)

В 1988 г. Юрг Фрёлих показал, что это действовало под спин-статистическая теорема чтобы обмен частицами был моноидальным (неабелева статистика).^[19] В частности, это может быть достигнуто, когда система демонстрирует некоторое вырождение, так что несколько различных состояний системы имеют одинаковую конфигурацию частиц. Тогда обмен частицами может способствовать не только фазовому переходу, но может отправить систему в другое состояние с той же конфигурацией частиц. В этом случае обмен частицами соответствует линейному преобразованию на этом подпространстве вырожденных состояний. Когда нет вырождения, это подпространство одномерно, и поэтому все такие линейные преобразования коммутируют (потому что они просто умножения на фазовый множитель). Когда есть вырождение и это подпространство имеет более высокую размерность, тогда эти линейные преобразования не должны коммутировать (как и умножение матриц).

Грегори Мур, Николас Рид, и Сяо-Ган Вэнь указал, что неабелева статистика может быть реализована в дробный квантовый эффект Холла (FQHE).^[20][21] В то время как поначалу неабелевы анионы обычно считались математическим курьезом, физики начали продвигаться к их открытию, когда Алексей Китаев показал, что неабелевы энионы могут быть использованы для построения топологический квантовый компьютер. По состоянию на 2012 год ни один эксперимент не продемонстрировал окончательно существование неабелевых энионов, хотя многообещающие намеки появляются при исследовании состояния ν = 5/2 FQHE.^[22][23] Экспериментальные свидетельства неабелевых эйонов, хотя еще не окончательные и оспариваемые,^[24] был представлен в октябре 2013 года.^[25]

Слияние аньонов

Примерно так же, как два фермиона (например, оба со спином 1/2) можно рассматривать вместе как составной бозон (с полным спином в суперпозиция из 0 и 1) два или более эниона вместе составляют составной энион (возможно, бозон или фермион). Составной энион называется результатом слияние его компонентов.

Если ${ displaystyle N}$ идентичные абелевы энионы, каждый с индивидуальной статистикой ${ displaystyle alpha}$ (то есть система берет фазу ${ Displaystyle е ^ {я альфа}}$ когда два отдельных эниона подвергаются адиабатическому обмену против часовой стрелки) все сливаются вместе, они вместе имеют статистику ${ displaystyle N ^ {2} alpha}$. В этом можно убедиться, заметив, что при вращении против часовой стрелки двух составных энионов друг относительно друга возникают ${ displaystyle N ^ {2}}$ пары отдельных энионов (один в первом составном энионе, один во втором составном энионе), каждый из которых вносит фазу ${ Displaystyle е ^ {я альфа}}$. Аналогичный анализ применим к слиянию неидентичных абелевых энионов. Статистика составного эниона однозначно определяется статистикой его компонентов.

Неабелевы анионы имеют более сложные отношения слияния. Как правило, в системе с неабелевыми энионами есть составная частица, статистическая метка которой не определяется однозначно статистическими метками ее компонентов, а существует как квантовая суперпозиция (это полностью аналогично тому, как два фермиона известны иметь спин 1/2 вместе в квантовой суперпозиции полного спина 1 и 0). Если общая статистика слияния всех нескольких энионов известна, остается неоднозначность слияния некоторых подмножеств этих энионов, и каждая возможность представляет собой уникальное квантовое состояние. Эти несколько состояний обеспечивают Гильбертово пространство на котором могут быть выполнены квантовые вычисления.^[26]

Топологическая основа

Вращение против часовой стрелки

Вращение по часовой стрелке

Обмен двумя частицами в пространстве-времени 2 + 1 путем вращения. Вращения неэквивалентны, поскольку одно не может быть деформировано в другое (без выхода мировых линий из плоскости, что невозможно в 2-м пространстве).

Более чем в двух измерениях спин-статистическая теорема утверждает, что любое многочастичное состояние неразличимые частицы должен подчиняться статистике Бозе – Эйнштейна или Ферми – Дирака. Для любого d > 2, Группы Ли ТАК(d,1) (который обобщает Группа Лоренца ) и Пуанкаре (d,1) имеют Z₂ как их первая гомотопическая группа. Поскольку циклическая группа Z₂ состоит из двух элементов, остаются только две возможности. (Детали более сложны, но это решающий момент.)

Ситуация меняется в двух измерениях. Здесь первая гомотопическая группа SO (2,1), а также Пуанкаре (2,1) - это Z (бесконечный циклический). Это означает, что Spin (2,1) не является универсальный чехол: это не так односвязный. В деталях есть проективные представления из специальная ортогональная группа SO (2,1), которые не возникают из линейные представления SO (2,1) или его двойная крышка, то вращательная группа Спин (2,1). Энионы - это равномерно дополнительные представления спиновой поляризации заряженной частицы.

Эта концепция также применима к нерелятивистским системам. Важная часть здесь состоит в том, что группа пространственного вращения SO (2) имеет бесконечную первую гомотопическую группу.

Этот факт также связан с группы кос хорошо известен в теория узлов. Это соотношение можно понять, если учесть тот факт, что в двух измерениях группа перестановок двух частиц больше не является симметричная группа S₂ (с двумя элементами), а скорее группа кос B₂ (с бесконечным количеством элементов). Существенным моментом является то, что одна коса может наматываться на другую, и эту операцию можно выполнять бесконечно часто, как по часовой, так и против часовой стрелки.

Совершенно иной подход к проблеме устойчивости-декогеренции в квантовые вычисления заключается в создании топологический квантовый компьютер с анионами, квазичастицами, используемыми в качестве нитей и полагающимися на теория кос сформировать стабильный логические ворота.^[27][28]

Многомерное обобщение анионов

Фракционные возбуждения в качестве точечных частиц могут быть бозонами, фермионами или энионами в пространственно-временном измерении 2 + 1. Известно, что точечные частицы могут быть либо бозонами, либо фермионами в пространственно-временном измерении 3 + 1 и выше. Однако петля (или струна) или мембранные возбуждения - протяженные объекты могут иметь дробную статистику. Текущие исследования показывают, что петлеобразные и струнные возбуждения существуют для топологические порядки в 3 + 1-мерном пространстве-времени, и их статистика многопетлевых / плетеных нитей является ключевыми сигнатурами для идентификации 3 + 1-мерных топологических порядков.^[29][30][31] Статистика многопетлевых / плетеных нитей 3 + 1-мерных топологических порядков может быть захвачена инвариантами ссылок конкретных топологические квантовые теории поля в четырех измерениях пространства-времени.^[31] Объясняя в разговорной манере, протяженные объекты (петля, струна, мембрана и т. Д.) Могут быть потенциально анионными в 3 + 1 и более высоких измерениях пространства-времени в дальнем диапазоне. запутанные системы.

Смотрите также

• Аньонная алгебра Ли - Подмножество алгебры
• Флюсовая трубка - Трубчатая область пространства с постоянным магнитным потоком по всей длине
• Теория Гинзбурга – Ландау - Теория сверхпроводимости
• Представление Хусими Q - Инструмент моделирования вычислительной физики
• Эффект джозефсона - Квантовое физическое явление
• Макроскопические квантовые явления - Процессы, демонстрирующие квантовое поведение в макроскопическом масштабе, а не в атомном масштабе, где преобладают квантовые эффекты; Квантовая когерентность макроскопического масштаба приводит к макроскопическим квантовым явлениям
• Магнитный домен - Область магнитного материала, в которой намагниченность имеет однородное направление
• Квант магнитного потока - Квантованная единица магнитного потока
• Эффект Мейснера - Излучение магнитного поля из сверхпроводника при его переходе в сверхпроводящее состояние
• Plekton - Теоретическая частица
• Квантовый вихрь - Квантованная циркуляция потока некоторой физической величины
• Случайная матрица - Матричнозначная случайная величина
• Топологический дефект - Тип структуры в квантовой механике
• Топологические квантовые вычисления - Гипотетический отказоустойчивый квантовый компьютер на основе топологической конденсированной среды

использованная литература

дальнейшее чтение

• Наяк, Четан; Саймон, Стивен Х .; Стерн, Ади; Фридман, Майкл; Дас Сарма, Санкар (2008). «Неабелевы анионы и топологические квантовые вычисления». Обзоры современной физики. 80 (3): 1083. arXiv:0707.1889. Bibcode:2008РвМП ... 80.1083Н. Дои:10.1103 / RevModPhys.80.1083.
• Вэнь Сяо-Ган (15 апреля 2002 г.). «Квантовые порядки и симметричные спиновые жидкости» (PDF). Физический обзор B. 65 (16): 165113. arXiv:cond-mat / 0107071. Bibcode:2002PhRvB..65p5113W. Дои:10.1103 / PhysRevB.65.165113. Архивировано из оригинал (PDF) 9 июня 2011 г.
• Стерн, Ади (2008). «Энионы и квантовый эффект Холла - педагогический обзор» (PDF). Анналы физики. 323: 204. arXiv:0711.4697. Bibcode:2008AnPhy.323..204S. Дои:10.1016 / j.aop.2007.10.008.
• Наджар, Дана (2020). "'Milestone "Свидетельства для Anyons, третьего королевства частиц". Журнал Quanta.