Статистика Бозе – Эйнштейна - Bose–Einstein statistics

В квантовая статистика, Статистика Бозе – Эйнштейна (B – E) описать один из двух возможных способов, которыми совокупность невзаимодействующих, неразличимых частицы может занимать набор доступных дискретных энергетические состояния в термодинамическое равновесие. Агрегация частиц в одном и том же состоянии, которая является характеристикой частиц, подчиняющихся статистике Бозе – Эйнштейна, объясняет когезионное течение свет лазера и ползание без трения сверхтекучий гелий. Теория такого поведения была разработана (1924–25) Сатьендра Нат Бос, который осознал, что таким образом можно распределить совокупность одинаковых и неотличимых частиц. Позднее идея была принята и расширена Альберт Эйнштейн в сотрудничестве с Bose.

Статистика Бозе-Эйнштейна применима только к тем частицам, которые не ограничиваются однократным заселением одного и того же состояния, то есть к частицам, которые не подчиняются Принцип исключения Паули ограничения. Такие частицы имеют целые значения вращение и названы бозоны, после статистики, которая правильно описывает их поведение. Между частицами также не должно быть значительного взаимодействия.

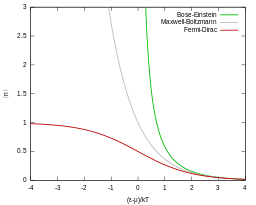
Сравнение средней занятости основного состояния по трем статистическим данным

Распределение Бозе – Эйнштейна

При низких температурах бозоны ведут себя иначе, чем фермионы (которые подчиняются Статистика Ферми – Дирака ) таким образом, что неограниченное количество из них может «конденсироваться» в одно и то же энергетическое состояние. Это явно необычное свойство также приводит к особому состоянию материи - Конденсат Бозе – Эйнштейна. Статистика Ферми – Дирака и Бозе – Эйнштейна применима, когда квантовые эффекты важны, а частицы "неотличимый ". Квантовые эффекты возникают, если концентрация частиц удовлетворяет

{ displaystyle { frac {N} {V}} geq n_ {q},}

где $N$ - количество частиц, $V$ объем, а $п q$ это квантовая концентрация, для которых межчастичное расстояние равно тепловая длина волны де Бройля, таким образом волновые функции частиц практически не перекрываются.

Статистика Ферми – Дирака применима к фермионам (частицам, которые подчиняются Принцип исключения Паули ), а статистика Бозе – Эйнштейна применяется к бозоны. Поскольку квантовая концентрация зависит от температуры, большинство систем при высоких температурах подчиняются классическому пределу (Максвелла – Больцмана), если только они не имеют очень высокую плотность, как в случае белый Гном. И Ферми – Дирак, и Бозе – Эйнштейн становятся Статистика Максвелла – Больцмана при высокой температуре или при низкой концентрации.

B – E статистика была введена для фотоны в 1924 г. Bose и обобщен на атомы Эйнштейн в 1924–25.

Ожидаемое количество частиц в энергетическом состоянии я для статистики B – E:

${ displaystyle { bar {n}} _ {i} = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { text {B}} T} -1}}}$

с $ε я > μ$ и где $п я$ это количество частиц в состоянии $я$ по общему количеству частиц всех энергетических состояний. $грамм я$ это вырождение уровня энергии $я, ε я$ это энергия из я-е состояние, μ это химический потенциал, $k B$ это Постоянная Больцмана, и Т является абсолютная температура.

Для сравнения, среднее количество фермионов с энергией ${ Displaystyle varepsilon _ {я}}$ данный Распределение частиц Ферми – Дирака по энергиям имеет похожую форму:

{ displaystyle { bar {n}} _ {i} ( varepsilon _ {i}) = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k_ { text {B}} T} +1}}.}

Как упоминалось выше, как распределение Бозе – Эйнштейна, так и распределение Ферми – Дирака приближаются к Распределение Максвелла – Больцмана в пределе высокой температуры и низкой плотности частиц, без необходимости каких-либо специальных предположений:

В пределе низкой плотности частиц ${ displaystyle { bar {n}} _ {i} = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { text {B}} T} pm 1}} ll 1}$ , следовательно ${ Displaystyle е ^ {( varepsilon _ {я} - mu) / к _ { текст {B}} T} pm 1 gg 1}$ или эквивалентно ${ Displaystyle е ^ {( varepsilon _ {я} - mu) / к _ { текст {B}} T} gg 1}$ . В таком случае, ${ displaystyle { bar {n}} _ {i} приблизительно { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { text {B}} T }}} = { frac {1} {Z}} e ^ {- varepsilon _ {i} / k _ { text {B}} T}}$ , который является результатом статистики Максвелла-Больцмана.
В пределе высокой температуры частицы распределены в большом диапазоне значений энергии, поэтому заселенность каждого состояния (особенно высокоэнергетического с ${ displaystyle varepsilon _ {i} - mu gg k _ { text {B}} T}$ ) снова очень мало, ${ displaystyle { bar {n}} _ {i} = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { text {B}} T} pm 1}} ll 1}$ . Это снова сводится к статистике Максвелла-Больцмана.

Помимо сокращения до Распределение Максвелла – Больцмана в пределе высокого ${ displaystyle T}$ и низкой плотности, B – E-статистика также сводится к Закон Рэлея – Джинса распределение для низкоэнергетических состояний с
${ displaystyle varepsilon _ {i} - mu ll k _ { text {B}} T}$ , а именно

{ displaystyle { begin {align} { bar {n}} _ {i} & = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { текст {B}} T} -1}} & приблизительно { frac {g_ {i}} {( varepsilon _ {i} - mu) / k _ { text {B}} T}} = { frac {g_ {i} k _ { text {B}} T} { varepsilon _ {i} - mu}}. end {выравнивается}}}

История

Читая лекцию на Университет Дакки (в том, что было тогда Британская Индия и сейчас Бангладеш ) по теории излучения и ультрафиолетовая катастрофа, Сатьендра Нат Бос стремился показать своим ученикам, что современная теория неадекватна, потому что она предсказывала результаты не в соответствии с результатами экспериментов. Во время этой лекции Бозе допустил ошибку в применении теории, которая неожиданно дала предсказание, совпадающее с экспериментом. Ошибка была простой ошибкой - подобной утверждению, что подбрасывание двух честных монет дает две орла в одной трети времени - что может показаться явно неправильным любому, кто имеет базовое понимание статистики (примечательно, что эта ошибка напоминала знаменитую ошибку д'Аламбер известно из его Croix ou Pile статья^[1]^[2]). Однако предсказанные результаты совпали с экспериментом, и Бозе понял, что это, возможно, не ошибка. Впервые он занял позицию, что Распределение Максвелла – Больцмана не будет верным для всех микроскопических частиц во всех масштабах. Таким образом, он изучил вероятность нахождения частиц в различных состояниях в фазовом пространстве, где каждое состояние представляет собой небольшой фрагмент с фазовым объемом час³, а положение и импульс частиц особо не разделяются, а рассматриваются как одна переменная.

Бозе преобразовал эту лекцию в небольшую статью под названием Закон Планка и гипотеза световых квантов^[3]^[4] и представил его Философский журнал. Однако заключение рецензента было отрицательным, и статья была отклонена. Неустрашимый, он отправил рукопись Альберту Эйнштейну с просьбой опубликовать ее в Zeitschrift für Physik. Эйнштейн немедленно согласился, лично перевел статью с английского на немецкий (Бозе ранее перевел статью Эйнштейна по общей теории относительности с немецкого на английский) и позаботился о том, чтобы она была опубликована. Теория Бозе получила признание, когда Эйнштейн отправил свою статью в поддержку теории Бозе в Zeitschrift für Physikс просьбой опубликовать их вместе. Газета вышла в 1924 году.^[5]

Причина, по которой Бозе дал точные результаты, заключалась в том, что, поскольку фотоны неотличимы друг от друга, нельзя рассматривать любые два фотона, имеющие равные квантовые числа (например, поляризацию и вектор импульса), как два отдельных идентифицируемых фотона. По аналогии, если бы в альтернативной вселенной монеты вели себя как фотоны и другие бозоны, вероятность образования двух голов действительно составляла бы одну треть, равно как и вероятность получения головы и хвоста, которая равна половине для обычные (классические, различимые) монеты. «Ошибка» Бозе приводит к тому, что сейчас называется статистикой Бозе – Эйнштейна.

Бозе и Эйнштейн распространили эту идею на атомы, и это привело к предсказанию существования явлений, которые стали известны как Конденсат Бозе – Эйнштейна, плотный набор бозонов (частиц с целочисленным спином, названный в честь Бозе), существование которого было продемонстрировано экспериментально в 1995 году.

Вывод

Вывод из микроканонического ансамбля

в микроканонический ансамбль, рассматривается система с фиксированными энергией, объемом и числом частиц. Возьмем систему, состоящую из ${ Displaystyle N = сумма _ {я} п_ {я}}$ одинаковые бозоны, ${ displaystyle n_ {i}}$ из которых имеют энергию ${ Displaystyle varepsilon _ {я}}$ и распределяются по ${ displaystyle g_ {i}}$ уровни или состояния с одинаковой энергией ${ Displaystyle varepsilon _ {я}}$ , т.е. ${ displaystyle g_ {i}}$ это вырождение, связанное с энергией ${ Displaystyle varepsilon _ {я}}$ общей энергии ${ Displaystyle Е = сумма _ {я} п_ {я} varepsilon _ {я}}$ . Расчет количества аранжировок ${ displaystyle n_ {i}}$ частицы распределены среди ${ displaystyle g_ {i}}$ государства - это проблема комбинаторика. Поскольку здесь частицы и состояния неразличимы в квантовомеханическом контексте, и начиная с состояния, количество расположений равно

{ displaystyle w _ { text {BE}} = { frac {(g + n-1)!} {n! (g-1)!}} = C_ {n} ^ {g + n-1}, }

где ${ displaystyle C_ {k} ^ {m}}$ это k-комбинация набора с м элементы.

Если мы начнем с частицы, число будет

{ displaystyle w _ { text {BE}} ^ {*} = { frac {(g + n-1)!} {g! , (n-1)!}} = C_ {g} ^ {g + n-1}.}

Сумма

{ displaystyle w _ { text {BE}} ^ {'} = { frac {(g + n)!} {g! , n!}} = C_ {g} ^ {g + n}.}

Поскольку здесь все числа большие, различие не имеет значения в данном контексте. Общее количество расположений в ансамбле бозонов равно

{ displaystyle W _ { text {BE}} = prod _ {i} { frac {(n_ {i} + g_ {i} -1)!} {(g_ {i} -1)! n_ {i }!}}.}

Максимальное количество расположений, определяющее соответствующий номер занятия ${ displaystyle n_ {i}}$ получается при поиске условия, которое максимизирует энтропия, или, что эквивалентно, установка ${ displaystyle mathrm {d} ( ln W _ { text {BE}}) = 0}$ и принимая дополнительные условия ${ displaystyle N = sum n_ {i}, E = sum _ {i} n_ {i} varepsilon _ {i}}$ во внимание (как Множители Лагранжа ).^[6] Результатом для большого числа частиц является распределение Бозе – Эйнштейна.

Выражения ${ displaystyle w _ { text {BE}}, w _ { text {BE}} ^ {*}}$ представляют значительный интерес во многих задачах комбинаторики. Для не огромных значений ${ displaystyle n}$ и ${ displaystyle g}$ то биномиальные коэффициенты ${ displaystyle C_ {r} ^ {n}, C_ {r} ^ {n + r-1}}$ даны Треугольники Паскаля. Дополнительные сведения о комбинаторике см. В примечаниях к каноническому выводу.

Выход из большого канонического ансамбля

Распределение Бозе – Эйнштейна, применимое только к квантовой системе невзаимодействующих бозонов, естественным образом выводится из большой канонический ансамбль без каких-либо приближений.^[7] В этом ансамбле система способна обмениваться энергией и обмениваться частицами с резервуаром (температура Т и химический потенциал µ фиксируется резервуаром).

Из-за того, что качество не взаимодействует, каждый доступный одночастичный уровень (с уровнем энергии ϵ) образует отдельную термодинамическую систему, контактирующую с резервуаром. То есть количество частиц в общей системе которые занимают данное одночастичное состояние образуют суб-ансамбль, который также является большим каноническим ансамблем; следовательно, его можно проанализировать, построив большая функция раздела.

Каждое одночастичное состояние имеет фиксированную энергию, ${ displaystyle varepsilon}$ . Поскольку суб-ансамбль, связанный с одночастичным состоянием, изменяется только числом частиц, ясно, что полная энергия суб-ансамбля также прямо пропорциональна числу частиц в одночастичном состоянии; где ${ displaystyle N}$ - количество частиц, тогда полная энергия суб-ансамбля будет ${ Displaystyle N varepsilon}$ . Начиная со стандартного выражения для большой функции раздела и заменяя ${ displaystyle E}$ с ${ Displaystyle N varepsilon}$ , большая статистическая сумма принимает вид

{ displaystyle { mathcal {Z}} = sum _ {N} exp ((N mu -N varepsilon) / k _ { text {B}} T) = sum _ {N} exp ( N ( mu - varepsilon) / k _ { text {B}} T)}

Эта формула применима как к фермионным системам, так и к бозонным системам. Статистика Ферми-Дирака возникает при рассмотрении влияния Принцип исключения Паули: в то время как количество фермионов, занимающих одно и то же одночастичное состояние, может быть только 1 или 0, количество бозонов, занимающих одночастичное состояние, может быть любым целым числом. Таким образом, большую статистическую сумму для бозонов можно рассматривать как геометрическая серия и могут быть оценены как таковые:

{ Displaystyle { begin {align} { mathcal {Z}} & = sum _ {N = 0} ^ { infty} exp (N ( mu - varepsilon) / k _ { text {B} } T) = sum _ {N = 0} ^ { infty} [ exp (( mu - varepsilon) / k _ { text {B}} T)] ^ {N} & = { гидроразрыв {1} {1- exp (( mu - varepsilon) / k _ { text {B}} T)}}. end {выравнивается}}}

Отметим, что геометрический ряд сходится, только если ${ Displaystyle е ^ {( му - varepsilon) / к _ { текст {B}} T} <1}$ , включая случай, когда ${ displaystyle epsilon = 0}$ . Это означает, что химический потенциал бозе-газа должен быть отрицательным, т. Е. ${ displaystyle mu <0}$ , в то время как ферми-газ может принимать как положительные, так и отрицательные значения химического потенциала.^[8]

Среднее число частиц для этого одночастичного подсостояния определяется как

{ displaystyle langle N rangle = k _ { text {B}} T { frac {1} { mathcal {Z}}} left ({ frac { partial { mathcal {Z}}} { partial mu}} right) _ {V, T} = { frac {1} { exp (( varepsilon - mu) / k _ { text {B}} T) -1}}}

Этот результат применим для каждого одночастичного уровня и, таким образом, образует распределение Бозе – Эйнштейна для всего состояния системы.^[9]^[10]

Разница в количестве частиц (из-за тепловые колебания ) также может быть получен, результат может быть выражен через ${ Displaystyle langle N rangle}$ только что полученное значение:

{ displaystyle langle sigma _ {N} ^ {2} rangle = k _ { text {B}} T left ({ frac {d langle N rangle} {d mu}} right) _ {V, T} = { frac { exp (( varepsilon - mu) / k _ { text {B}} T)} {( exp (( varepsilon - mu) / k _ { text {B}} T) -1) ^ {2}}} = langle N rangle (1+ langle N rangle).}

В результате для сильно занятых государств среднеквадратичное отклонение числа частиц на уровне энергии очень велико, немного больше, чем само число частиц: ${ displaystyle sigma _ {N} приблизительно langle N rangle}$ . Эта большая неопределенность связана с тем, что распределение вероятностей для числа бозонов на данном уровне энергии есть геометрическое распределение; несколько парадоксально, наиболее вероятное значение для N всегда 0. (Напротив, классические частицы иметь вместо распределение Пуассона в количестве частиц для данного состояния с гораздо меньшей неопределенностью ${ displaystyle sigma _ {N, { rm {classic}}} = { sqrt { langle N rangle}}}$ , а с наиболее вероятным N ценность быть рядом ${ Displaystyle langle N rangle}$ .)

Вывод в каноническом подходе

Также возможно получить приближенную статистику Бозе – Эйнштейна в канонический ансамбль Эти выводы являются длинными и приводят только к приведенным выше результатам в асимптотическом пределе большого числа частиц. Причина в том, что полное число бозонов фиксировано в каноническом ансамбле. Распределение Бозе – Эйнштейна в этом случае может быть получено, как и в большинстве текстов, путем максимизации, но математически лучший вывод получается с помощью Метод Дарвина – Фаулера средних значений, как подчеркивал Дингл.^[11] См. Также Мюллер-Кирстен.^[6] Однако флуктуации основного состояния в конденсированной области заметно различаются в каноническом и великоканоническом ансамблях.^[12]

Вывод

Предположим, у нас есть несколько уровней энергии, помеченных индексом ${ displaystyle displaystyle i}$ , каждый уровень имеет энергию ${ Displaystyle Displaystyle varepsilon _ {я}}$ и содержащий в общей сложности ${ displaystyle displaystyle n_ {i}}$ частицы. Предположим, что каждый уровень содержит ${ displaystyle displaystyle g_ {i}}$ различные подуровни, все из которых имеют одинаковую энергию и различимы. Например, две частицы могут иметь разные импульсы, и в этом случае они отличны друг от друга, но при этом могут иметь одинаковую энергию. Значение ${ displaystyle displaystyle g_ {i}}$ связанный с уровнем ${ displaystyle displaystyle i}$ называется «вырождением» этого энергетического уровня. На одном подуровне может находиться любое количество бозонов.

Позволять ${ Displaystyle Displaystyle ш (п, г)}$ быть количеством способов распределения ${ displaystyle displaystyle n}$ частицы среди ${ displaystyle displaystyle g}$ подуровни энергетического уровня. Есть только один способ распространения ${ displaystyle displaystyle n}$ частицы с одним подуровнем, поэтому ${ Displaystyle Displaystyle ш (п, 1) = 1}$ . Нетрудно заметить, что есть ${ Displaystyle Displaystyle (п + 1)}$ способы распространения ${ displaystyle displaystyle n}$ частицы на двух подуровнях, которые мы запишем как:

{ displaystyle w (n, 2) = { frac {(n + 1)!} {n! 1!}}.}.

Немного подумав (см. Примечания ниже) видно, что количество способов раздачи ${ displaystyle displaystyle n}$ частиц в трех подуровнях

{ Displaystyle вес (п, 3) = вес (п, 2) + вес (п-1,2) + cdots + вес (1,2) + вес (0,2)}

так что

{ displaystyle w (n, 3) = sum _ {k = 0} ^ {n} w (nk, 2) = sum _ {k = 0} ^ {n} { frac {(n-k + 1)!} {(Nk)! 1!}} = { Frac {(n + 2)!} {N! 2!}}}

где мы использовали следующие теорема с привлечением биномиальные коэффициенты:

{ displaystyle sum _ {k = 0} ^ {n} { frac {(k + a)!} {k! a!}} = { frac {(n + a + 1)!} {п! (а + 1)!}}.}

Продолжая этот процесс, мы видим, что ${ Displaystyle Displaystyle ш (п, г)}$ просто биномиальный коэффициент (см. Примечания ниже)

{ displaystyle w (n, g) = { frac {(n + g-1)!} {n! (g-1)!}}.}.

Например, численность населения для двух частиц на трех подуровнях составляет 200, 110, 101, 020, 011 или 002, всего шесть, что равно 4! / (2! 2!). Количество способов, которыми набор номеров занятий ${ displaystyle displaystyle n_ {i}}$ может быть реализовано, является продуктом способов, которыми может быть заполнен каждый индивидуальный энергетический уровень:

{ displaystyle W = prod _ {i} w (n_ {i}, g_ {i}) = prod _ {i} { frac {(n_ {i} + g_ {i} -1)!} { n_ {i}! (g_ {i} -1)!}} приблизительно prod _ {i} { frac {(n_ {i} + g_ {i})!} {n_ {i}! (g_ { я})!}}}

где приближение предполагает, что ${ displaystyle n_ {i} gg 1}$ .

Следуя той же процедуре, которая использовалась при вычислении Статистика Максвелла – Больцмана, мы хотим найти набор ${ displaystyle displaystyle n_ {i}}$ для которого W максимизируется при условии, что существует фиксированное общее количество частиц и фиксированная общая энергия. Максимумы ${ displaystyle displaystyle W}$ и ${ Displaystyle Displaystyle ln (W)}$ происходят при том же значении ${ displaystyle displaystyle n_ {i}}$ и, поскольку это проще выполнить математически, мы вместо этого максимизируем последнюю функцию. Мы ограничиваем наше решение, используя Множители Лагранжа формирование функции:

{ Displaystyle е (п_ {я}) = пер (W) + альфа (N- сумма п_ {я}) + бета (E- сумма п_ {я} varepsilon _ {я})}

С использованием ${ displaystyle n_ {i} gg 1}$ приближение и использование Приближение Стирлинга для факториалов ${ displaystyle left (x! приблизительно x ^ {x} , e ^ {- x} , { sqrt {2 pi x}} right)}$ дает

{ displaystyle f (n_ {i}) = sum _ {i} (n_ {i} + g_ {i}) ln (n_ {i} + g_ {i}) - n_ {i} ln (n_ {i}) + alpha left (N- sum n_ {i} right) + beta left (E- sum n_ {i} varepsilon _ {i} right) + K.}

Где K представляет собой сумму ряда членов, которые не являются функциями ${ displaystyle n_ {i}}$ . Взяв производную по ${ displaystyle displaystyle n_ {i}}$ , и установив результат равным нулю и решив для ${ displaystyle displaystyle n_ {i}}$ , дает численность населения Бозе – Эйнштейна:

{ displaystyle n_ {i} = { frac {g_ {i}} {e ^ { alpha + beta varepsilon _ {i}} - 1}}.}

Процессом, аналогичным описанному в Статистика Максвелла – Больцмана статье видно, что:

{ Displaystyle д пер W = альфа , dN + бета , dE}

которое, используя известное соотношение Больцмана ${ Displaystyle S = к _ { текст {B}} , ln W}$ становится заявлением второй закон термодинамики при постоянной громкости, и отсюда следует, что ${ displaystyle beta = { frac {1} {k _ { text {B}} T}}}$ и ${ displaystyle alpha = - { гидроразрыва { mu} {k _ { text {B}} T}}}$ где S это энтропия, ${ displaystyle mu}$ это химический потенциал, k_B является Постоянная Больцмана и Т это температура, так что наконец:

{ displaystyle n_ {i} = { frac {g_ {i}} {e ^ {( varepsilon _ {i} - mu) / k _ { text {B}} T} -1}}.}

Обратите внимание, что приведенная выше формула иногда записывается:

{ displaystyle n_ {i} = { frac {g_ {i}} {e ^ { varepsilon _ {i} / k _ { text {B}} T} / z-1}},}

где ${ Displaystyle Displaystyle Z = ехр ( му / к _ { текст {B}} T)}$ это абсолют Мероприятия, как отмечает МакКуорри.^[13]

Также обратите внимание, что когда числа частиц не сохраняются, снятие ограничения сохранения числа частиц эквивалентно установке ${ displaystyle alpha}$ и, следовательно, химический потенциал ${ displaystyle mu}$ до нуля. Это будет иметь место для фотонов и массивных частиц во взаимном равновесии, и результирующее распределение будет Распределение Планка.

Примечания

Гораздо более простой способ представить себе функцию распределения Бозе – Эйнштейна - это учесть, что п частицы обозначены одинаковыми шарами и Оболочки g отмечены перегородками линии g-1. Понятно, что перестановки из этих n мячей и г - 1 перегородки даст разные способы расположения бозонов на разных уровнях энергии. Скажем, для 3 (=п) частиц и 3 (=грамм) оболочки, поэтому (грамм - 1) = 2, расположение могло бы быть |●●|●, или же ||●●●, или же |●|●● и т. д. Следовательно, количество различных перестановок n + (g-1) объектов, которые имеют n идентичных элементов и (грамм - 1) идентичные предметы будут:

{ displaystyle { frac {(g-1 + n)!} {(g-1)! n!}}}

ИЛИ ЖЕ

Цель этих заметок - прояснить некоторые аспекты вывода распределения Бозе – Эйнштейна (B – E) для начинающих. Перечень случаев (или способов) в распределении B – E можно изменить следующим образом. Рассмотрим игру в бросание костей, в которой ${ displaystyle displaystyle n}$ кости, каждая из которых принимает значения в наборе ${ Displaystyle Displaystyle {1, точки, г }}$ , за ${ displaystyle g geq 1}$ . Ограничения игры заключаются в том, что значение кубика ${ displaystyle displaystyle i}$ , обозначаемый ${ displaystyle displaystyle m_ {i}}$ , должно быть больше или равно ценность смерти ${ Displaystyle Displaystyle (я-1)}$ , обозначаемый ${ Displaystyle Displaystyle м_ {я-1}}$ , в предыдущем броске, т.е. ${ Displaystyle м_ {я} geq м_ {я-1}}$ . Таким образом, правильную последовательность бросков кубика можно описать ппара ${ displaystyle displaystyle (m_ {1}, m_ {2}, dots, m_ {n})}$ , так что ${ Displaystyle м_ {я} geq м_ {я-1}}$ . Позволять ${ Displaystyle Displaystyle S (п, г)}$ обозначим множество этих допустимых п- пары:

${ Displaystyle S (n, g) = { Big {} (m_ {1}, m_ {2}, dots, m_ {n}) { Big |} { Big.} m_ {i} geq m_ {i-1}, m_ {i} in left {1, ldots, g right }, forall i = 1, dots, n { Big }}.}$

(1)

Тогда количество ${ Displaystyle Displaystyle ш (п, г)}$ (определено выше как количество способов распространения ${ displaystyle displaystyle n}$ частицы среди ${ displaystyle displaystyle g}$ подуровней энергетического уровня) - мощность ${ Displaystyle Displaystyle S (п, г)}$ , то есть количество элементов (или действительных п-tuples) в ${ Displaystyle Displaystyle S (п, г)}$ Таким образом, проблема нахождения выражения для ${ Displaystyle Displaystyle ш (п, г)}$ становится проблемой подсчета элементов в ${ Displaystyle Displaystyle S (п, г)}$ .

пример п = 4, грамм = 3:

{ Displaystyle S (4,3) = влево { underbrace {(1111), (1112), (1113)} _ {(a)}, underbrace {(1122), (1123), (1133) } _ {(b)}, underbrace {(1222), (1223), (1233), (1333)} _ {(c)}, right.}

{ displaystyle left. underbrace {(2222), (2223), (2233), (2333), (3333)} _ {(d)} right }}

{ Displaystyle Displaystyle ш (4,3) = 15}

(есть

{ displaystyle displaystyle 15}

элементы в

{ Displaystyle Displaystyle S (4,3)}

)

Подмножество ${ Displaystyle Displaystyle (а)}$ получается фиксацией всех индексов ${ displaystyle displaystyle m_ {i}}$ к ${ displaystyle displaystyle 1}$ , кроме последнего индекса, ${ displaystyle displaystyle m_ {n}}$ , который увеличивается с ${ displaystyle displaystyle 1}$ к ${ displaystyle displaystyle g = 3}$ .Подмножество ${ displaystyle displaystyle (b)}$ получается путем фиксации ${ Displaystyle Displaystyle м_ {1} = м_ {2} = 1}$ , и увеличивая ${ displaystyle displaystyle m_ {3}}$ из ${ displaystyle displaystyle 2}$ к ${ displaystyle displaystyle g = 3}$ . Из-за ограничения ${ Displaystyle Displaystyle м_ {я} geq м_ {я-1}}$ по индексам в ${ Displaystyle Displaystyle S (п, г)}$ , индекс ${ displaystyle displaystyle m_ {4}}$ должен автоматически принимать значения в ${ Displaystyle Displaystyle влево {2,3 вправо }}$ .Построение подмножеств. ${ Displaystyle Displaystyle (с)}$ и ${ displaystyle displaystyle (d)}$ следует таким же образом.

Каждый элемент ${ Displaystyle Displaystyle S (4,3)}$ можно рассматривать как мультимножество мощности ${ Displaystyle Displaystyle п = 4}$ ; элементы такого мультимножества берутся из множества ${ Displaystyle Displaystyle влево {1,2,3 вправо }}$ мощности ${ displaystyle displaystyle g = 3}$ , а количество таких мультимножеств равно коэффициент мультимножества

{ displaystyle displaystyle left langle { begin {matrix} 3 4 end {matrix}} right rangle = {3 + 4-1 choose 3-1} = {3 + 4-1 выберите 4} = { frac {6!} {4! 2!}} = 15}

В более общем плане каждый элемент ${ Displaystyle Displaystyle S (п, г)}$ это мультимножество мощности ${ displaystyle displaystyle n}$ (количество кубиков) с элементами, взятыми из набора ${ Displaystyle Displaystyle влево {1, точки, г вправо }}$ мощности ${ displaystyle displaystyle g}$ (количество возможных значений каждого кубика) и количество таких мультимножеств, т. е. ${ Displaystyle Displaystyle ш (п, г)}$ это коэффициент мультимножества

${ displaystyle displaystyle w (n, g) = left langle { begin {matrix} g n end {matrix}} right rangle = {g + n-1 select g-1} = {g + n-1 choose n} = { frac {(g + n-1)!} {n! (g-1)!}}}$

(2)

который в точности совпадает с формула за ${ Displaystyle Displaystyle ш (п, г)}$ , как получено выше с помощью теорема с биномиальными коэффициентами, а именно

${ displaystyle sum _ {k = 0} ^ {n} { frac {(k + a)!} {k! a!}} = { frac {(n + a + 1)!} {п! (а + 1)!}}.}$

(3)

Чтобы понять разложение

${ Displaystyle Displaystyle вес (N, g) = sum _ {k = 0} ^ {n} вес (nk, g-1) = w (n, g-1) + w (n-1, g- 1) + cdots + w (1, g-1) + w (0, g-1)}$

(4)

или, например, ${ Displaystyle Displaystyle п = 4}$ и ${ displaystyle displaystyle g = 3}$

{ Displaystyle Displaystyle вес (4,3) = вес (4,2) + вес (3,2) + вес (2,2) + вес (1,2) + вес (0,2),}

давайте переставим элементы ${ Displaystyle Displaystyle S (4,3)}$ следующим образом

{ Displaystyle S (4,3) = влево { underbrace {(1111), (1112), (1122), (1222), (2222)} _ {( alpha)}, underbrace {(111 { color {Red} { underset {=} {3}}}), (112 { color {Red} { underset {=} {3}}}), (122 { color {Red} { underset {=} {3}}}), (222 { color {Red} { underset {=} {3}}})} _ {( beta)}, right.}

{ displaystyle left. underbrace {(11 { color {Red} { underset {==} {33}}}), (12 { color {Red} { underset {==} {33}} }), (22 { color {Red} { underset {==} {33}}})} _ {( gamma)}, underbrace {(1 { color {Red} { underset {== =} {333}}}), (2 { color {Red} { underset {===} {333}}})} _ {( delta)} underbrace {({ color {Red} { underset {====} {3333}}})} _ {( omega)} right }.}

Ясно, что подмножество ${ Displaystyle Displaystyle ( альфа)}$ из ${ Displaystyle Displaystyle S (4,3)}$ такой же, как и набор

{ Displaystyle Displaystyle S (4,2) = влево {(1111), (1112), (1122), (1222), (2222) вправо }}

.

Удалив индекс ${ displaystyle displaystyle m_ {4} = 3}$ (Показано в красный с двойным подчеркиванием) в подмножестве ${ Displaystyle Displaystyle ( бета)}$ из ${ Displaystyle Displaystyle S (4,3)}$ , получаем набор

{ Displaystyle Displaystyle S (3,2) = влево {(111), (112), (122), (222) вправо }}

.

Другими словами, существует взаимно однозначное соответствие между подмножеством ${ Displaystyle Displaystyle ( бета)}$ из ${ Displaystyle Displaystyle S (4,3)}$ и набор ${ Displaystyle Displaystyle S (3,2)}$ . Мы пишем

{ Displaystyle Displaystyle ( бета) longleftrightarrow S (3,2)}

.

Аналогичным образом легко увидеть, что

{ displaystyle displaystyle ( gamma) longleftrightarrow S (2,2) = left {(11), (12), (22) right }}

{ Displaystyle Displaystyle ( дельта) longleftrightarrow S (1,2) = влево {(1), (2) вправо }}

{ displaystyle displaystyle ( omega) longleftrightarrow S (0,2) = varnothing}

(пустой набор).

Таким образом, мы можем написать

{ Displaystyle Displaystyle S (4,3) = bigcup _ {k = 0} ^ {4} S (4-k, 2)}

или, в более общем смысле,

${ Displaystyle Displaystyle S (п, г) = bigcup _ {к = 0} ^ {п} S (п-к, г-1)}$ ;

(5)

а поскольку множества

{ Displaystyle S (я, г-1), { текст {для}} я = 0, точки, п}

не пересекаются, поэтому

${ Displaystyle Displaystyle вес (п, г) = сумма _ {к = 0} ^ {п} вес (п-к, г-1)}$ ,

(6)

с условием, что

{ displaystyle w (0, g) = 1 , forall g, { text {and}} w (n, 0) = 1 , forall n.}

(7)

Продолжая процесс, приходим к следующей формуле

{ displaystyle w (n, g) = sum _ {k_ {1} = 0} ^ {n} sum _ {k_ {2} = 0} ^ {n-k_ {1}} w (n-k_ {1} -k_ {2}, g-2) = sum _ {k_ {1} = 0} ^ {n} sum _ {k_ {2} = 0} ^ {n-k_ {1}} cdots sum _ {k_ {g} = 0} ^ {n- sum _ {j = 1} ^ {g-1} k_ {j}} w (n- sum _ {i = 1} ^ {g } k_ {i}, 0).}

Используя соглашение (7)₂ выше, получаем формулу

${ displaystyle displaystyle w (n, g) = sum _ {k_ {1} = 0} ^ {n} sum _ {k_ {2} = 0} ^ {n-k_ {1}} cdots сумма _ {k_ {g} = 0} ^ {n- sum _ {j = 1} ^ {g-1} k_ {j}} 1,}$

(8)

имея в виду, что для ${ displaystyle displaystyle q}$ и ${ displaystyle displaystyle p}$ будучи константами, мы имеем

${ displaystyle displaystyle sum _ {k = 0} ^ {q} p = qp}$ .

(9)

Затем можно проверить, что (8) и (2) дают одинаковый результат для ${ Displaystyle Displaystyle ш (4,3)}$ , ${ Displaystyle Displaystyle ш (3,3)}$ , ${ Displaystyle Displaystyle ш (3,2)}$ , так далее.

Междисциплинарные приложения

Рассматривается как чистый распределение вероятностей, распределение Бозе – Эйнштейна нашло применение в других областях:

В последние годы статистика Бозе-Эйнштейна также использовалась в качестве метода взвешивания терминов в поиск информации. Этот метод является одним из набора моделей DFR («Дивергенция от случайности»),^[14] основная идея заключается в том, что статистика Бозе-Эйнштейна может быть полезным индикатором в тех случаях, когда конкретный термин и конкретный документ имеют значимую взаимосвязь, которая не возникла бы случайно. Исходный код для реализации этой модели доступен на сайте Терьер проект в Университете Глазго.
Эволюция многих сложных систем, в том числе Всемирная паутина, бизнес и сети цитирования, закодированы в динамической сети, описывающей взаимодействия между составляющими системы. Несмотря на свою необратимую и неравновесную природу, эти сети следуют статистике Бозе и могут подвергаться конденсации Бозе – Эйнштейна. Обращение к динамическим свойствам этих неравновесных систем в рамках равновесных квантовых газов предсказывает, что «преимущество первопроходца», «приспособляемость и обогащение» (FGR), и явления «победитель получает все», наблюдаемые в конкурентных системах, являются термодинамически различными фазами лежащих в основе развивающихся сетей.[15]

Смотрите также

Примечания

^ Даламбер, Жан (1754). "Croix ou pile". L'Encyclopédie (На французском). 4.
^ Даламбер, Жан (1754). "CROIX OU PILE" [Перевод Ричарда Дж. Пулскэмпа] (PDF). Ксавье университет. Получено 2019-01-14.
^ См. Стр. 14, примечание 3 диссертации: Микеланджели, Алессандро (октябрь 2007 г.). Конденсация Бозе – Эйнштейна: анализ проблем и строгие результаты (PDF) (Кандидат наук.). Международная школа перспективных исследований. В архиве (PDF) из оригинала 3 ноября 2018 г.. Получено 14 февраля 2019. Сложить резюме.
^ Бозе (2 июля 1924 г.). «Закон Планка и гипотеза световых квантов» (PostScript). Ольденбургский университет. Получено 30 ноября 2016.
^ Бозе (1924), "Plancks Gesetz und Lichtquantenhypothese", Zeitschrift für Physik (на немецком), 26 (1): 178–181, Bibcode:1924ZPhy ... 26..178B, Дои:10.1007 / BF01327326, S2CID 186235974
^ ^а ^б H.J.W. Мюллер-Кирстен, Основы статистической физики, 2-е изд., World Scientific (2013), ISBN 978-981-4449-53-3.
^ Srivastava, R.K .; Ашок, Дж. (2005). «Глава 7». Статистическая механика. Нью-Дели: PHI Learning Pvt. ООО ISBN 9788120327825.
^ Ландау, Л. Д., Лифшич, Э. М., Лифшиц, Э. М., и Питаевский, Л. П. (1980). Статистическая физика (Том 5). Pergamon Press.
^ "Глава 6". Статистическая механика. Январь 2005 г. ISBN 9788120327825.
^ Распределение BE может быть получено также из теории теплового поля.
^ Р. Б. Дингл, Асимптотические разложения: их вывод и интерпретация, Academic Press (1973), стр. 267–271.
^ Ziff R.M; Kac, M .; Уленбек, Г. Э. (1977). "Новый взгляд на идеальный газ Бозе – Эйнштейна. " Phys. Отчеты 32: 169-248.
^ См. McQuarrie в цитатах
^ Amati, G .; К. Дж. Ван Рейсберген (2002). "Вероятностные модели поиска информации на основе измерения отклонения от случайности " ACM TOIS 20(4):357–389.
^ Бьянкони, Г.; Барабаши, А.-Л. (2001). "Конденсация Бозе – Эйнштейна в сложных сетях. " Phys. Rev. Lett. 86: 5632–35.

Статистическая механика
Теория	Принцип максимальной энтропии эргодическая теория
Статистическая термодинамика	Ансамбли функции раздела уравнения состояния термодинамический потенциал: U ЧАС F г Максвелл отношения
Модели	Модели ферромагнетизма Я пою Potts Гейзенберг просачивание Частицы с силовое поле сила истощения Потенциал Леннарда-Джонса
Математические подходы	Уравнение Больцмана H-теорема Уравнение Власова BBGKY иерархия случайный процесс теория среднего поля и конформная теория поля
Критические явления	Фаза перехода Критические показатели длина корреляции масштабирование по размеру
Энтропия	Больцман Шеннон Цаллис Реньи фон Нейман
Приложения	Статистическая теория поля элементарная частица сверхтекучесть физика конденсированного состояния сложная система хаос теория информации Машина Больцмана

Альберт Эйнштейн
Физика	Специальная теория относительности Общая теория относительности Эквивалентность массы и энергии (E = mc²) Броуновское движение Фотоэлектрический эффект Коэффициенты Эйнштейна Эйнштейн твердый Принцип эквивалентности Уравнения поля Эйнштейна Радиус Эйнштейна Соотношение Эйнштейна (кинетическая теория) Космологическая постоянная Конденсат Бозе – Эйнштейна Статистика Бозе – Эйнштейна Корреляции Бозе – Эйнштейна Теория Эйнштейна – Картана Уравнения Эйнштейна – Инфельда – Гофмана. Эффект Эйнштейна – де Гааза Парадокс ЭПР Дебаты Бора и Эйнштейна Телепараллелизм Мысленные эксперименты Неудачные расследования Дуальность волна-частица Гравитационная волна Парадокс чайного листа
Работает	Аннус Мирабилис документы (1905) "Исследования по теории броуновского движения " (1905) Относительность: специальная и общая теория (1916) Смысл теории относительности (1922) Мир, каким я его вижу (1934) Эволюция физики (1938) "Почему социализм? " (1949) Манифест Рассела-Эйнштейна (1955)
Семья	Полина Кох (мать) Герман Эйнштейн (отец) Майя Эйнштейн (сестра) Милева Марич (первая жена) Эльза Эйнштейн (вторая жена; двоюродная сестра) Лизерл Эйнштейн (дочь) Ганс Альберт Эйнштейн (сын) Эдуард Эйнштейн (сын) Бернхард Цезарь Эйнштейн (внук) Эвелин Эйнштейн (внучка) Томас Мартин Эйнштейн (правнук) Роберт Эйнштейн (двоюродный брат) Зигберт Эйнштейн (Дальний родственник)
В популярных культура	Die Grundlagen der Einsteinschen Relativitäts-Theorie (Документальный фильм 1922 года) Теория относительности Эйнштейна (Документальный фильм 1923 года) Реликвии: мозг Эйнштейна (Документальный фильм 1994 года) Незначительность (Фильм 1985 года) I.Q. (Фильм 1994 года) Дар Эйнштейна (Спектакль 2003 года) Эйнштейн и Эддингтон (Телефильм 2008 года) Гений (Серия 2017 г.)
Связанный	Награды и отличия Мозг жилой дом Мемориал Политические взгляды Религиозные взгляды Список вещей, названных в честь Альберта Эйнштейна Архив Альберта Эйнштейна Проект документов Эйнштейна Эйнштейн холодильник Эйнштейнхаус Эйнштейний
Призы	Премия Альберта Эйнштейна Медаль Альберта Эйнштейна Медаль ЮНЕСКО Альберта Эйнштейна Премия мира Альберта Эйнштейна Мировая премия имени Альберта Эйнштейна в области науки Премия Эйнштейна в области лазерной науки Премия Эйнштейна (APS)
Книги о Эйнштейн	Альберт Эйнштейн: Создатель и бунтарь Эйнштейн и религия Эйнштейн для начинающих Эйнштейн: его жизнь и Вселенная Космос Эйнштейна Я Альберт Эйнштейн Введение в относительность Тонкий Господь
Книга Категория

Статистика Бозе – Эйнштейна - Bose–Einstein statistics

Содержание

Распределение Бозе – Эйнштейна

История

Вывод

Вывод из микроканонического ансамбля

Выход из большого канонического ансамбля

Вывод в каноническом подходе

Междисциплинарные приложения

Смотрите также

Примечания

Рекомендации