Радиус Эйнштейна - Einstein radius

В Радиус Эйнштейна это радиус Кольцо Эйнштейна, - характерный угол для гравитационное линзирование в общем, поскольку типичные расстояния между изображениями при гравитационном линзировании порядка радиуса Эйнштейна.^[1]

Вывод

Геометрия гравитационных линз

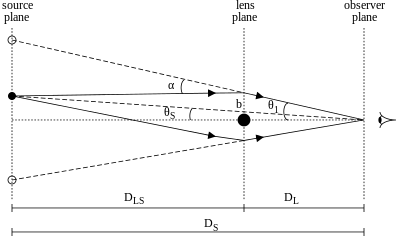
При следующем выводе радиуса Эйнштейна мы будем предполагать, что вся масса M линзирующей галактики L сосредоточен в центре галактики.

Для точечной массы прогиб может быть вычислен и является одним из классических тесты общей теории относительности. Для малых углов α₁ полное отклонение точечной массой M дан (см. Метрика Шварцшильда ) к

${displaystyle alpha _ {1} = {frac {4G} {c ^ {2}}} {frac {M} {b_ {1}}}}$

куда

б₁ это прицельный параметр (расстояние ближайшего приближения светового луча к центру масс)

грамм это гравитационная постоянная,

c это скорость света.

Отметив, что для малых углов и угла, выраженного в радианы, точка ближайшего подхода б₁ под углом θ₁ для объектива L на расстоянии D_L дан кем-то б₁ = θ₁ D_L, мы можем переопределить угол изгиба α₁ в качестве

${displaystyle alpha _ {1} (heta _ {1}) = {frac {4G} {c ^ {2}}} {frac {M} {heta _ {1}}} {frac {1} {D_ {m {L}}}}}$ ..... (Уравнение 1)

Если мы установим θ_S как угол, под которым можно было бы видеть источник без линзы (что обычно не наблюдается), и θ₁ как наблюдаемый угол изображения источника по отношению к линзе, то из геометрии линзирования (считая расстояния в плоскости источника) можно увидеть, что вертикальное расстояние, охватываемое углом θ₁ На расстоянии D_S совпадает с суммой двух вертикальных расстояний θ_S D_S и α₁ D_LS. Это дает уравнение линзы

${displaystyle heta _ {1}; D_ {m {S}} = heta _ {m {S}}; D_ {m {S}} + alpha _ {1}; D_ {m {LS}}}$

который можно переставить, чтобы получить

${displaystyle alpha _ {1} (heta _ {1}) = {frac {D_ {m {S}}} {D_ {m {LS}}}}} (heta _ {1} - heta _ {m {S} })}$ ..... (уравнение 2)

Установив (уравнение 1) равным (уравнение 2) и переставив, мы получаем

${displaystyle heta _ {1} - heta _ {m {S}} = {frac {4G} {c ^ {2}}}; {frac {M} {heta _ {1}}}; {frac {D_ { м {LS}}} {D_ {m {S}} D_ {m {L}}}}}$

Для источника прямо за объективом θ_S = 0уравнение линзы для точечной массы дает характерное значение для θ₁ это называется Угол Эйнштейна, обозначенный θ_E. Когда θ_E выражается в радианах, а источник линзирования находится достаточно далеко, Радиус Эйнштейна, обозначенный р_E, дан кем-то

${displaystyle R_ {E} = heta _ {E} D_ {m {L}}}$. ^[2]

Положив θ_S = 0 и решение для θ₁ дает

${displaystyle heta _ {E} = left ({frac {4GM} {c ^ {2}}}; {frac {D_ {m {LS}}}} {D_ {m {L}} D_ {m {S}}) }} ight) ^ {1/2}}$

Угол Эйнштейна для точечной массы обеспечивает удобную линейную шкалу для безразмерных переменных линзирования. В терминах угла Эйнштейна уравнение линзы для точечной массы принимает вид

${displaystyle heta _ {1} = heta _ {m {S}} + {frac {heta _ {E} ^ {2}} {heta _ {1}}}}$

Подстановка констант дает

${displaystyle heta _ {E} = left ({frac {M} {10 ^ {11.09} M_ {igodot}}} ight) ^ {1/2} left ({frac {D_ {m {L}} D_ {m) {S}} / D_ {m {LS}}} {m {Gpc}}} ight) ^ {- 1/2} {m {arcsec}}}$

В последнем виде масса выражается в солнечные массы (M_☉ и расстояния в гигахпарсек (Гпк). Радиус Эйнштейна наиболее заметен для линзы, обычно на полпути между источником и наблюдателем.

Для плотного кластера с массой M_c ≈ 10×10¹⁵ M_☉ на расстоянии 1 гигапарсек (1 Гпк) этот радиус может достигать 100 угловых секунд (так называемый макролинзирование). Для Гравитационное микролинзирование мероприятие (с массой порядка 1 M_☉) искать на галактических расстояниях (скажем, D ~ 3 кпк), типичный радиус Эйнштейна будет порядка милли арсекунд. Следовательно, отдельные изображения в событиях микролинзирования невозможно наблюдать с помощью современных методов.

Точно так же для ниже луч света, достигающий наблюдателя из-под линзы, имеем

${displaystyle heta _ {2}; D_ {m {S}} = -; heta _ {m {S}}; D_ {m {S}} + alpha _ {2}; D_ {m {LS}}}$

и

${displaystyle heta _ {2} + heta _ {m {S}} = {frac {4G} {c ^ {2}}}; {frac {M} {heta _ {2}}}; {frac {D_ { м {LS}}} {D_ {m {S}} D_ {m {L}}}}}$

и поэтому

${displaystyle heta _ {2} = -; heta _ {m {S}} + {frac {heta _ {E} ^ {2}} {heta _ {2}}}}$

Приведенный выше аргумент может быть расширен для линз, которые имеют распределенную массу, а не точечную массу, путем использования другого выражения для угла изгиба α, положения θ_я(θ_S) изображений можно затем рассчитать. Для небольших отклонений это отображение является взаимно однозначным и состоит из искажений наблюдаемых положений, которые являются обратимыми. Это называется слабое линзирование. Для больших отклонений можно иметь несколько изображений и необратимое отображение: это называется сильное линзирование. Обратите внимание, что для того, чтобы распределенная масса приводила к кольцу Эйнштейна, оно должно быть осесимметричным.

Смотрите также

• Гравитационная линза
• Кольцо Эйнштейна

Рекомендации

Библиография

• Чвольсон, О. (1924). "Über eine mögliche Form fiktiver Doppelsterne". Astronomische Nachrichten. 221 (20): 329–330. Bibcode:1924AN .... 221..329C. Дои:10.1002 / asna.19242212003. (Первая статья, предлагающая кольца)
• Эйнштейн, Альберт (1936). «Линзовидное действие звезды при отклонении света в гравитационном поле» (PDF). Наука. 84 (2188): 506–507. Bibcode:1936Sci .... 84..506E. Дои:10.1126 / science.84.2188.506. JSTOR  1663250. PMID  17769014. (Знаменитая статья о кольцах Эйнштейна)
• Ренн, Юрген; Тилман Зауэр и Джон Стачел (1997). «Происхождение гравитационного линзирования: постскриптум к научной статье Эйнштейна 1936 года». Наука. 275 (5297): 184–186. Bibcode:1997Sci ... 275..184R. Дои:10.1126 / science.275.5297.184. PMID  8985006.