Гравитационное микролинзирование - Gravitational microlensing

Часть цикла статей о
Гравитационное линзирование
Кольцо Эйнштейна Формализм Сильное линзирование Микролинзирование Слабое линзирование
Системы сильных линз Абель 1689  · Абель 2218 CL0024 + 17  · Пуля кластера QSO2237 + 0305  · SDSSJ0946 + 1006 B1359 + 154  · QSO 0957 + 561
Обзоры Сильный: УЧЕБНЫЙ КЛАСС  · SLACS (SDSS ) Микро: OGLE  · Гайя Слабый: DLS  · Пан-СТАРРС  · CFHTLS  · DES  · LSST  · ЩЕЛЧОК  · СУДЬБА

Гравитационное микролинзирование является астрономический явление из-за гравитационная линза эффект. Его можно использовать для обнаружения объектов, масса которых варьируется от массы планеты до массы звезды, независимо от излучаемого ими света. Обычно астрономы могут обнаруживать только яркие объекты, излучающие много света (звезды ) или большие объекты, которые блокируют фоновый свет (облака газа и пыли). Эти объекты составляют лишь небольшую часть массы галактики. Микролинзирование позволяет изучать объекты, которые излучают мало света или вообще не излучают его.

Анимация гравитационного микролинзирования

Когда далекая звезда или квазар достаточно выровнен с массивным компактным объектом переднего плана, искривление света из-за его гравитационного поля, как обсуждалось Альберт Эйнштейн в 1915 г. приводит к двум искаженным неразрешенным изображениям, приводящим к заметному увеличению. Временной масштаб кратковременного повышения яркости зависит от массы объекта переднего плана, а также от относительного собственного движения между фоновым «источником» и объектом «линза» переднего плана.

Идеально выровненное микролинзирование создает чистый буфер между излучением линзы и объектами-источниками. Он увеличивает удаленный источник, раскрывая его или увеличивая его размер и / или яркость. Это позволяет изучать совокупность тусклых или темных объектов, таких как коричневые карлики, красные карлики, планеты, белые карлики, нейтронные звезды, черные дыры, и массивные компактные гало-объекты. Такое линзирование работает на всех длинах волн, увеличивая и создавая широкий диапазон возможных искажений для удаленных источников, которые излучают любой вид электромагнитного излучения.

Микролинзирование изолированным объектом было впервые обнаружено в 1989 году. С тех пор микролинзирование использовалось для ограничения природы темная материя, обнаружить экзопланеты, изучать потемнение конечностей в далеких звездах сдерживайте двойная звезда населения и ограничивают структуру диска Млечного Пути. Микролинзирование также предлагалось как средство обнаружения темных объектов, таких как коричневые карлики и черные дыры. звездные пятна, измерять вращение звезд и исследовать квазары^[1][2] включая их аккреционные диски.^[3][4][5][6] Микролинзирование использовалось в 2018 году для обнаружения Икар, самая далекая из когда-либо наблюдавшихся звезд.^[7][8]

Как это устроено

Микролинзирование основано на гравитационная линза эффект. Массивный объект (линза) будет отклонять свет яркого фонового объекта (источника). Это может создавать несколько искаженных, увеличенных и ярких изображений источника фона.^[9]

Микролинзирование вызывается тем же физическим эффектом, что и сильное линзирование и слабое линзирование, но оно изучается с использованием очень разных методов наблюдения. При сильном и слабом линзировании масса линзы достаточно велика (масса галактики или скопления галактик), чтобы смещение света линзой можно было разрешить с помощью телескопа высокого разрешения, такого как Космический телескоп Хаббла. При микролинзировании масса линзы слишком мала (масса планеты или звезды) для того, чтобы можно было легко наблюдать смещение света, но видимое увеличение яркости источника все же можно обнаружить. В такой ситуации линза пройдет мимо источника за разумное время, от секунд до лет вместо миллионов лет. Когда выравнивание изменяется, видимая яркость источника изменяется, и это можно отслеживать, чтобы обнаружить и изучить событие. Таким образом, в отличие от сильных и слабых гравитационных линз, событие микролинзирования - это временное явление с точки зрения человеческого масштаба.^[10]

В отличие от сильного и слабого линзирования, ни одно наблюдение не может установить наличие микролинзирования. Вместо этого необходимо отслеживать увеличение и уменьшение яркости источника с течением времени с помощью фотометрия. Эта функция яркости в зависимости от времени известна как кривая блеска. Типичная кривая блеска при микролинзировании показана ниже:

Типичное событие микролинзирования, подобное этому, имеет очень простую форму, и можно выделить только один физический параметр: масштаб времени, который связан с массой линзы, расстоянием и скоростью. Однако есть несколько эффектов, которые влияют на форму более нетипичных событий линзирования:

• Распределение линз по массе. Если масса линзы не сосредоточена в одной точке, кривая блеска может сильно отличаться, особенно с едкий - события пересечения, которые могут иметь сильные всплески на кривой блеска. При микролинзировании это можно увидеть, когда линза двойная звезда или планетная система.
• Конечный размер источника. В чрезвычайно ярких или быстро меняющихся событиях микролинзирования, таких как события пересечения каустики, звезду-источник нельзя рассматривать как бесконечно маленькую светящуюся точку: размером с диск звезды и даже потемнение конечностей может изменять экстремальные характеристики.
• Параллакс. Для событий, продолжающихся месяцами, движение Земли вокруг Солнца может вызвать небольшое изменение выравнивания, что повлияет на кривую блеска.

В настоящее время наибольшее внимание уделяется более необычным явлениям микролинзирования, особенно тем, которые могут привести к открытию внесолнечных планет. Другой способ получить больше информации о событиях микролинзирования - это измерение астрометрический смещения исходной позиции в ходе события^[11] и даже разрешение отдельных изображений с интерферометрия.^[12] Первое успешное разрешение изображений микролинзирования было достигнуто с помощью прибора GRAVITY на Интерферометр очень большого телескопа (VLTI).^[13]

Наблюдение за микролинзированием

Объект, вызывающий микролинзирование в NGC 6553 искривлял свет красной гигантской звезды на заднем плане.^[14][15]

На практике, поскольку необходимое выравнивание настолько точное и трудно предсказуемое, микролинзирование встречается очень редко. Следовательно, события обычно обнаруживаются с помощью обзоров, которые фотометрически отслеживают десятки миллионов потенциальных звезд-источников каждые несколько дней в течение нескольких лет. Плотные фоновые поля, подходящие для таких обзоров, - это близлежащие галактики, такие как Магеллановы Облака и галактика Андромеды, а также балдж Млечный Путь. В каждом случае исследуемая популяция линзы включает объекты между Землей и полем источника: для балджа населением линзы являются звезды диска Млечного Пути, а для внешних галактик населением линзы является гало Млечного Пути, а также объекты. в самой другой галактике. Плотность, масса и расположение объектов в этих группах линз определяют частоту микролинзирования вдоль этого луча зрения, которая характеризуется величиной, известной как оптическая глубина из-за микролинзирования. (Не следует путать с более распространенным значением слова оптическая глубина (хотя у него есть некоторые свойства.) Оптическая толщина - это, грубо говоря, средняя доля звезд-источников, подвергающихся микролинзированию в данный момент времени, или, что эквивалентно, вероятность того, что данная звезда-источник подвергается линзированию в данный момент времени. В рамках проекта MACHO оптическая глубина в сторону БМО составила 1,2 × 10⁻⁷,^[16] а оптическая глубина в сторону балджа - 2,43 × 10⁻⁶ или примерно 1 из 400 000.^[17]

Поиск усложняет тот факт, что на каждую звезду, подвергающуюся микролинзированию, приходится тысячи звезд, меняющих яркость по другим причинам (около 2% звезд в типичном поле источника естественно переменные звезды ) и другие переходные события (такие как новые и сверхновые ), и их необходимо отсеять, чтобы найти истинные события микролинзирования. После того, как событие микролинзирования было идентифицировано, программа мониторинга, которая его обнаруживает, часто предупреждает сообщество о своем открытии, чтобы другие специализированные программы могли более интенсивно следить за событием, надеясь найти интересные отклонения от типичной кривой блеска. Это связано с тем, что эти отклонения - особенно из-за экзопланет - требуют почасового мониторинга для выявления, который программы исследований не могут обеспечить, пока все еще ищут новые события. Вопрос о том, как расставить приоритеты в происходящих событиях для детального наблюдения с ограниченными ресурсами наблюдения, очень важен для исследователей микролинзирования сегодня.

История

В 1704 г. Исаак Ньютон предположил, что луч света может отклоняться под действием силы тяжести.^{[нужна цитата ]} В 1801 г. Иоганн Георг фон Зольднер рассчитал величину отклонения светового луча от звезды под действием ньютоновской гравитации. В 1915 г. Альберт Эйнштейн правильно предсказал величину отклонения под Общая теория относительности, что было вдвое больше, чем предсказал фон Зольднер. Предсказание Эйнштейна было подтверждено экспедицией 1919 года под руководством Артур Эддингтон, что стало большим успехом для общей теории относительности.^[18] В 1924 г. Орест Чвольсон обнаружили, что линзирование может дать несколько изображений звезды. Правильный прогноз сопутствующего повышения яркости источника, лежащий в основе микролинзирования, был опубликован в 1936 году Эйнштейном.^[19] Из-за того, что требуется маловероятное выравнивание, он пришел к выводу, что «нет больших шансов наблюдать это явление». Современные теоретические основы гравитационного линзирования были заложены в работах Ю. Климова (1963), Сиднея Либеса (1964) и Сьюр Рефсдал (1964).^[1]

Гравитационное линзирование было впервые обнаружено в 1979 году в виде квазара, линзированного галактикой на переднем плане. В том же году Кёнгэ Чанг и Сьюр Рефсдал показали, что отдельные звезды в галактике-линзе могут действовать как линзы меньшего размера внутри основной линзы, вызывая колебания изображений квазара-источника с периодом в несколько месяцев, также известным как Линза Чанга – Рефсдала.^[20] Богдан Пачиньски впервые применил термин «микролинзирование» для описания этого явления. Этот тип микролинзирования трудно идентифицировать из-за внутренней изменчивости квазаров, но в 1989 году Майк Ирвин и др. опубликовано обнаружение микролинзирования в Линза Хухры.

В 1986 году Пачиньский предложил использовать микролинзирование для поиска темная материя в виде массивных компактных гало-объектов (МАЧО) в Галактическое гало, наблюдая за фоновыми звездами в соседней галактике. Две группы физиков элементарных частиц, работающих над темной материей, услышали его доклады и объединились с астрономами для создания англо-австралийского коллаборации MACHO.^[21] и французский EROS^[22] сотрудничество.

В 1986 г. Роберт Дж. Немирофф предсказал вероятность микролинзирования^[23] и рассчитал основные кривые блеска, вызванные микролинзированием, для нескольких возможных конфигураций линзы и источника в своей диссертации 1987 года.^[24]

В 1991 году Мао и Пачинский предположили, что микролинзирование может быть использовано для поиска двойных спутников звезд, а в 1992 году Гулд и Леб продемонстрировали, что микролинзирование можно использовать для обнаружения экзопланет. В 1992 году Пачиньский основал Оптическое гравитационное линзирование.,^[25] который начал поиск событий в направлении Галактический балдж. Первые два события микролинзирования в направлении Большое Магелланово Облако что могло быть вызвано темной материей, сообщалось один за другим Природа документы MACHO^[26] и ЭРОС^[27] в 1993 году и в последующие годы события продолжали обнаруживаться. Сотрудничество MACHO закончилось в 1999 году. Их данные опровергли гипотезу о том, что 100% темного ореола составляют MACHO, но они обнаружили значительное необъяснимое превышение примерно 20% массы ореола, которое могло быть связано с MACHO или линзами внутри Большого Само Магелланово Облако.^[28] Впоследствии EROS опубликовал еще более строгие верхние пределы для MACHO,^[29] и в настоящее время неясно, есть ли какой-либо избыток микролинзирования гало, который вообще может быть вызван темной материей. Проект СуперМАХО^[30] В настоящее время ведется поиск линз, ответственных за результаты MACHO.

Несмотря на то, что проблема темной материи не решена, микролинзирование оказалось полезным инструментом для многих приложений. Сотни событий микролинзирования регистрируются ежегодно в направлении Галактический балдж, где оптическая толщина микролинзирования (из-за звезд в диске Галактики) примерно в 20 раз больше, чем через гало Галактики. В 2007 году в рамках проекта OGLE было определено 611 кандидатов на проведение мероприятий, а в рамках проекта MOA (сотрудничество Японии и Новой Зеландии)^[31] выявлено 488 (хотя не все кандидаты оказываются объектами микролинзирования, и между двумя проектами наблюдается значительное совпадение). В дополнение к этим исследованиям, в настоящее время ведутся дополнительные проекты по детальному изучению потенциально интересных текущих событий, в первую очередь с целью обнаружения внесолнечных планет. К ним относятся MiNDSTEp,^[32] Робонет,^[33] MicroFUN^[34] и ПЛАНЕТА.^[35]

В сентябре 2020 года астрономы, использующие методы микролинзирования, сообщили о обнаружение, впервые масса земли планета-изгой неограничен какой-либо звездой и свободно плавает в Млечный путь.^[36][37]

Математика

Математика микролинзирования, наряду с современными обозначениями, описана Гулдом.^[38] и мы используем его обозначения в этом разделе, хотя другие авторы использовали другие обозначения. В Радиус Эйнштейна, также называемый углом Эйнштейна, является угловой радиус из Кольцо Эйнштейна в случае идеального выравнивания. Это зависит от массы линзы M, расстояния линзы d_L, а расстояние до источника d_S:

${ displaystyle theta _ {E} = { sqrt {{ frac {4GM} {c ^ {2}}} { frac {d_ {S} -d_ {L}} {d_ {S} d_ {L }}}}}}$ (в радианах).

Для M, равного 60 масс Юпитера, d_L = 4000 парсек, а d_S = 8000 парсек (типично для случая микролинзирования выпуклости), радиус Эйнштейна равен 0,00024 угловые секунды^[39] (угол наклона на 1 а.е. за 4000 парсеков).^[40] Для сравнения: идеальные наблюдения с Земли угловое разрешение около 0,4 угловой секунды, что в 1660 раз больше. С ${ displaystyle theta _ {E}}$ настолько мала, что обычно не наблюдается для типичного события микролинзирования, но может наблюдаться в некоторых экстремальных явлениях, как описано ниже.

Хотя нет четкого начала или конца события микролинзирования, по соглашению считается, что событие длится, пока угловое разделение между источником и линзой меньше ${ displaystyle theta _ {E}}$. Таким образом, продолжительность события определяется временем, за которое видимое движение линзы в небе преодолевает угловое расстояние. ${ displaystyle theta _ {E}}$. Радиус Эйнштейна также имеет тот же порядок величины, что и угловое разделение между двумя линзованными изображениями, и астрометрический сдвиг положений изображений в течение события микролинзирования.

Во время события микролинзирования яркость источника усиливается коэффициентом усиления A. Этот коэффициент зависит только от близости расположения наблюдателя, линзы и источника. Безразмерное число u определяется как угловое расстояние между линзой и источником, деленное на ${ displaystyle theta _ {E}}$. Коэффициент усиления выражается через это значение:^[41]

${ displaystyle A (u) = { frac {u ^ {2} +2} {u { sqrt {u ^ {2} +4}}}}.}.$

У этой функции есть несколько важных свойств. A (u) всегда больше 1, поэтому микролинзирование может только увеличить яркость звезды-источника, но не уменьшить ее. A (u) всегда уменьшается с увеличением u, поэтому чем ближе выравнивание, тем ярче становится источник. Когда u приближается к бесконечности, A (u) приближается к 1, так что при больших расстояниях микролинзирование не действует. Наконец, когда u приближается к 0, для точечного источника A (u) приближается к бесконечности, когда изображения приближаются к кольцу Эйнштейна. Для идеального выравнивания (u = 0) A (u) теоретически бесконечно. На практике объекты реального мира не являются точечными источниками, и эффекты конечного размера источника устанавливают предел того, насколько большое усиление может происходить при очень близком выравнивании,^[42] но некоторые события микролинзирования могут вызвать повышение яркости в сотни раз.

В отличие от гравитационного макролинзирования, где линза представляет собой галактику или скопление галактик, при микролинзировании u существенно изменяется за короткий период времени. Соответствующая шкала времени называется временем Эйнштейна. ${ displaystyle t_ {E}}$, и он определяется временем, которое требуется линзе, чтобы пройти угловое расстояние ${ displaystyle theta _ {E}}$ относительно источника в небе. Для типичных событий микролинзирования ${ displaystyle t_ {E}}$ составляет от нескольких дней до нескольких месяцев. Функция u (t) просто определяется теоремой Пифагора:

${ displaystyle u (t) = { sqrt {u_ {min} ^ {2} + left ({ frac {t-t_ {0}} {t_ {E}}} right) ^ {2}}) }.}$

Минимальное значение u, называемое u_мин, определяет максимальную яркость события.

В типичном случае микролинзирования кривая блеска хорошо подходит, если предположить, что источником является точка, линза представляет собой единую точечную массу, а линза движется по прямой линии: точечный источник-точечный объектив приближение. В этих событиях единственным физически значимым параметром, который можно измерить, является шкала времени Эйнштейна. ${ displaystyle t_ {E}}$. Поскольку эта наблюдаемая выродиться функции массы линзы, расстояния и скорости, мы не можем определить эти физические параметры из одного события.

Однако в некоторых экстремальных случаях ${ displaystyle theta _ {E}}$ могут быть измерены, в то время как другие экстремальные события могут исследовать дополнительный параметр: размер кольца Эйнштейна в плоскости наблюдателя, известный как Прогнозируемый радиус Эйнштейна: ${ displaystyle { tilde {r}} _ {E}}$. Этот параметр описывает, как событие будет выглядеть по-другому для двух наблюдателей в разных местах, таких как спутниковый наблюдатель. Прогнозируемый радиус Эйнштейна связан с физическими параметрами линзы и источника соотношением

${ displaystyle { tilde {r}} _ {E} = { sqrt {{ frac {4GM} {c ^ {2}}} { frac {d_ {S} d_ {L}} {d_ {S } -d_ {L}}}}}.}$

Математически удобно использовать обратные значения некоторых из этих величин. Это Эйнштейн правильное движение

${ displaystyle { vec { mu}} _ {E} = {t_ {E}} ^ {- 1}}$

и Эйнштейн параллакс

${ displaystyle { vec { pi}} _ {E} = {{ tilde {r}} _ {E}} ^ {- 1}.}$

Эти векторные величины указывают в направлении относительного движения линзы относительно источника. Некоторые экстремальные явления микролинзирования могут ограничивать только один компонент этих векторных величин. Если эти дополнительные параметры будут полностью измерены, физические параметры линзы могут быть решены, давая массу линзы, параллакс и собственное движение как

${ displaystyle M = { frac {c ^ {2}} {4G}} theta _ {E} { tilde {r}} _ {E},}$

${ displaystyle pi _ {L} = pi _ {E} theta _ {E} + pi _ {S},}$

${ displaystyle mu _ {L} = mu _ {E} theta _ {E} + mu _ {S}.}$

Экстремальные события микролинзирования

В типичном случае микролинзирования кривая блеска хорошо подходит, если предположить, что источником является точка, линза представляет собой единую точечную массу, а линза движется по прямой линии: точечный источник-точечный объектив приближение. В этих событиях единственным физически значимым параметром, который можно измерить, является шкала времени Эйнштейна. ${ displaystyle t_ {E}}$. Однако в некоторых случаях события могут быть проанализированы, чтобы получить дополнительные параметры угла Эйнштейна и параллакса: ${ displaystyle theta _ {E}}$ и ${ displaystyle pi _ {E}}$. К ним относятся события с очень большим увеличением, бинарные линзы, события параллакса и xallarap, а также события, при которых линза видна.

События, дающие угол Эйнштейна

Хотя угол Эйнштейна слишком мал, чтобы его можно было непосредственно увидеть в наземный телескоп, было предложено несколько методов его наблюдения.

Если линза проходит непосредственно перед звездой-источником, то конечный размер звезды-источника становится важным параметром. Звезду-источник следует рассматривать как диск на небе, а не точку, что нарушает приближение точечного источника и вызывает отклонение от традиционной кривой микролинзирования, которая длится столько времени, сколько линза пересекает источник, известное как а кривая блеска конечного источника. Длину этого отклонения можно использовать для определения времени, необходимого линзе, чтобы пересечь диск звезды-источника. ${ displaystyle t_ {S}}$. Если угловой размер источника ${ displaystyle theta _ {S}}$ известно, угол Эйнштейна можно определить как

${ displaystyle theta _ {E} = theta _ {S} { frac {t_ {E}} {t_ {S}}}.}$

Эти измерения редки, так как они требуют крайнего совмещения источника и линзы. Они более вероятны, когда ${ displaystyle theta _ {S} / theta _ {E}}$ является (относительно) большим, т.е.для близких гигантских источников с медленно движущимися маломассивными линзами вблизи источника.

В событиях с конечным источником различные части звезды-источника увеличиваются с разной скоростью в разное время во время события. Таким образом, эти события можно использовать для изучения потемнение конечностей исходной звезды.

Бинарные линзы

Если линза представляет собой двойную звезду с разделением примерно на радиус Эйнштейна, картина увеличения будет более сложной, чем в линзах одиночной звезды. В этом случае обычно есть три изображения, когда линза находится на расстоянии от источника, но есть диапазон выравнивания, при котором создаются два дополнительных изображения. Эти выравнивания известны как каустика. На этих юстировках увеличение источника формально бесконечно в приближении точечного источника.

Пересечение каустика в бинарных линзах может происходить с более широким диапазоном геометрии линз, чем в одиночной линзе. Подобно каустике источника с одной линзой, источнику требуется конечное время, чтобы пересечь каустику. Если это время пересечения каустики ${ displaystyle t_ {S}}$ можно измерить, и если известен угловой радиус источника, то снова можно определить угол Эйнштейна.

Как и в случае одиночной линзы, когда увеличение источника формально бесконечно, двойные линзы, пересекающие каустику, будут увеличивать различные части звезды-источника в разное время. Таким образом, они могут исследовать структуру источника и его потемнение к краю.

Анимацию события бинарной линзы можно найти на это видео на YouTube.

События, дающие параллакс Эйнштейна

В принципе, параллакс Эйнштейна можно измерить, если два наблюдателя одновременно наблюдают за событием из разных мест, например, с Земли и с удаленного космического корабля.^[43] Разница в усилении, наблюдаемая двумя наблюдателями, дает составляющую ${ displaystyle { vec { pi}} _ {E}}$ перпендикулярно движению линзы, в то время как разница во времени максимального усиления дает компонент, параллельный движению линзы. Об этом прямом измерении недавно было сообщено^[44] с использованием Космический телескоп Спитцера. В крайних случаях различия можно даже измерить по небольшим различиям, видимым в телескопы в разных местах на Земле.^[45]

Как правило, параллакс Эйнштейна измеряется по нелинейному движению наблюдателя, вызванному вращением Земли вокруг Солнца. Впервые об этом сообщили в 1995 году.^[46] и с тех пор о нем сообщалось в нескольких событиях. Параллакс в событиях с точечной линзой лучше всего измерять в событиях длительного времени с большим ${ displaystyle pi _ {E}}$- от медленно движущихся линз малой массы, находящихся близко к наблюдателю.

Если исходная звезда двойная звезда, то он тоже будет иметь нелинейное движение, которое также может вызвать небольшие, но заметные изменения кривой блеска. Этот эффект известен как Xallarap (параллакс пишется наоборот).

Обнаружение внесолнечных планет

Гравитационное микролинзирование внесолнечной планеты

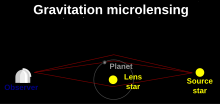
Если линзирующий объект - звезда с планетой, вращающейся вокруг нее, это крайний пример события двойной линзы. Если источник пересекает каустику, отклонения от стандартного события могут быть большими даже для планет с малой массой. Эти отклонения позволяют нам сделать вывод о существовании и определить массу и разделение планеты вокруг линзы. Отклонения обычно длятся несколько часов или несколько дней. Поскольку сигнал наиболее сильный, когда самое сильное событие, события с большим увеличением являются наиболее многообещающими кандидатами для подробного изучения. Обычно исследовательская группа уведомляет сообщество, когда обнаруживает, что происходит событие с большим увеличением. Группы последующего наблюдения затем интенсивно контролируют текущее событие, надеясь получить хорошее освещение отклонения, если оно произойдет. Когда событие закончилось, кривая блеска сравнивается с теоретическими моделями, чтобы определить физические параметры системы. Параметры, которые могут быть определены непосредственно из этого сравнения, - это отношение масс планеты к звезде и отношение углового расстояния между звездой и планетой к углу Эйнштейна. Из этих соотношений, наряду с предположениями о звезде-линзе, можно оценить массу планеты и ее орбитальное расстояние.

Экзопланеты, обнаруженные с помощью микролинзирования, по годам до 2014 года.

Первый успех этой техники был достигнут в 2003 году как OGLE, так и MOA в результате микролинзирования. OGLE 2003 – BLG – 235 (или MOA 2003 – BLG – 53). Объединив свои данные, они обнаружили, что наиболее вероятная масса планеты в 1,5 раза превышает массу Юпитера.^[47] По состоянию на апрель 2020 года этим методом было обнаружено 89 экзопланет.^[48] Известные примеры включают OGLE-2005-BLG-071Lb,^[49] OGLE-2005-BLG-390Lb,^[50] OGLE-2005-BLG-169Lb,^[51] две экзопланеты вокруг OGLE-2006-BLG-109L,^[52] и MOA-2007-BLG-192Lb.^[53] Примечательно, что на момент своего объявления в январе 2006 года планета OGLE-2005-BLG-390Lb, вероятно, имела самую низкую массу из всех известных экзопланет, вращающихся вокруг обычной звезды, со средней массой в 5,5 раза больше массы Земли и примерно в несколько раз больше. две неопределенности. В 2007 году этот рекорд оспаривал Gliese 581 c с минимальной массой 5 ​​масс Земли, а с 2009 г. Gliese 581 e это самая легкая из известных "обычных" экзопланет с минимальной массой 1.9 Земли. В октябре 2017 г. OGLE-2016-BLG-1190Lb, чрезвычайно массивная экзопланета (или, возможно, коричневый карлик ), что примерно в 13,4 раза больше массы Юпитер, Сообщалось.^[54]

Сравнение этого метода обнаружения внесолнечных планет с другими методами, такими как транзит Одним из преимуществ метода является то, что интенсивность планетарного отклонения не зависит от массы планеты так сильно, как эффекты в других методах. Это делает микролинзирование подходящим для поиска планет с малой массой. Он также позволяет обнаруживать планеты дальше от звезды-хозяина, чем большинство других методов. Одним из недостатков является то, что наблюдение за системой линз очень сложно после того, как событие закончилось, потому что требуется много времени, чтобы линза и источник были достаточно разделены для их разделения по отдельности.

А приземная атмосферная линза предложенный Ю Вангом в 1998 году, который будет использовать атмосферу Земли в качестве большой линзы, может также напрямую отображать близлежащие потенциально обитаемые экзопланеты.^[55]

Микролинзирующие эксперименты

Есть два основных типа экспериментов по микролинзированию. «Поисковые» группы используют изображения с большим полем для поиска новых событий микролинзирования. «Сопровождающие» группы часто координируют телескопы по всему миру, чтобы обеспечить интенсивное освещение избранных событий.Все первоначальные эксперименты носили несколько рискованные названия до образования группы PLANET. В настоящее время есть предложения о создании новых специализированных спутников для микролинзирования или об использовании других спутников для изучения микролинзирования.

Поиск сотрудничества

• Алард; Мао; Гвибер (1995). «Object DUO 2: новый кандидат на двоичную линзу». Астрономия и астрофизика. 300: L17. arXiv:Astro-ph / 9506101. Bibcode:1995A & A ... 300L..17A. Фотографическая пластина для поиска выпуклости.
• Experience de Recherche des Objets Sombres (EROS) (1993–2002) В основном французское сотрудничество. EROS1: Поиск фотопластинок LMC: EROS2: Поиск CCD LMC, SMC, выпуклостей и спиральных рукавов.
• МАЧО (1993–1999) Сотрудничество Австралии и США. ПЗС-поиск выпуклости и БМО.
• Эксперимент по оптическому гравитационному линзированию (OGLE) (1992 -), польское сотрудничество, основанное Пачинским и Удальский. Выделенный 1,3-метровый телескоп в Чили, управляемый Варшавским университетом. Цели на выпуклости и Магеллановых облаках.
• Наблюдения с помощью микролинзирования в астрофизике (MOA) (1998 -), японско-новозеландское сотрудничество. Выделенный телескоп 1,8 м в Новой Зеландии. Цели на выпуклости и Магеллановых облаках.
• СуперМАХО (2001 -), преемник коллаборации MACHO использовал 4-метровый телескоп CTIO для изучения слабых микролинз LMC.

Последующее сотрудничество

• Сеть зондирующих аномалий (PLANET) Многонациональное сотрудничество.
• MicroFUN, Сеть наблюдения за микролинзированием
• Поиск планеты с микролинзированием (MPS)
• Сеть микролинзирования для обнаружения малых экзопланет земного типа, MiNDSTEp
• Робонет. Поиск планет с помощью глобальной сети роботизированных телескопов

Сотрудничество с пиксельным линзированием галактики Андромеды

• МЕГА
• AGAPE (На французском)
• WeCAPP
• Проект Ангстрем
• СТРОИТЬ ПЛАНЫ

Предлагаемые спутниковые эксперименты

• Галактический телескоп для исследования экзопланет (GEST)
• Проект ключа микролинзирования SIM использовал бы чрезвычайно высокую точность астрометрия из Миссия космической интерферометрии спутник, чтобы сломать вырождение микролинзирования и измерить массу, расстояние и скорость линз. Этот спутник откладывался несколько раз и окончательно отменялся в 2010 году.
• Широкопольный инфракрасный обзорный телескоп - объекты астрофизического телескопа (WFIRST - AFTA) состоит в том, чтобы объединить съемку микролинзирования с несколькими другими задачами. Данные микролинзирования дополнят данные Кеплера с большей чувствительностью к планетам, таким как Земля, которые не находятся близко к своим солнцам.

Смотрите также

Гравитационная линза

Земная атмосферная линза

Рекомендации

внешняя ссылка

• Открытие планеты в пять раз массивнее Земли, вращающейся вокруг звезды на расстоянии 20 000 световых лет от нас.