Квантовое туннелирование - Quantum tunnelling
Квантовое туннелирование или туннелирование (США) - это квантово-механический явление, когда волновая функция может распространяться через потенциальный барьер.
Прохождение через барьер может быть конечным и экспоненциально зависит от высоты и ширины барьера. Волновая функция не исчезает с одной стороны и не появляется снова с другой. Волновая функция и ее первая производная находятся непрерывный. В установившемся режиме поток вероятности в прямом направлении пространственно однороден. Ни частица, ни волна не теряются. Туннелирование происходит с барьерами толщиной около 1–3 нм и меньше.[1]
Некоторые авторы также идентифицируют простое проникновение волновой функции в барьер без передачи на другую сторону как туннельный эффект. Квантовое туннелирование не предсказывается законами классическая механика где для преодоления потенциального барьера требуется потенциальная энергия.
Квантовое туннелирование играет важную роль в физических явлениях, таких как термоядерная реакция.[2] Она имеет Приложения в туннельный диод,[3] квантовые вычисления, а в сканирующий туннельный микроскоп.
Эффект был предсказан еще в начале 20 века. Его признание в качестве общего физического явления пришло к середине века.[4]
Предполагается, что квантовое туннелирование приведет к физическим ограничениям размера транзисторы используется в микроэлектроника из-за того, что электроны могут проходить мимо транзисторов, которые слишком малы.[5][6]
Туннелирование можно объяснить с точки зрения Принцип неопределенности Гейзенберга в том, что квантовый объект может быть известный как волна или как частица вообще. Другими словами, неопределенность точного местоположения легких частиц позволяет этим частицам нарушать правила классической механики и перемещаться в пространстве, не преодолевая барьер потенциальной энергии.
История
Квантовое туннелирование было разработано на основе изучения радиоактивность,[4] который был открыт в 1896 г. Анри Беккерель.[7] Радиоактивность была дополнительно исследована Мари Кюри и Пьер Кюри, за что они заработали Нобелевская премия по физике в 1903 г.[7] Эрнест Резерфорд и Эгон Швайдлер изучил его природу, что впоследствии было подтверждено эмпирически Фридрих Кольрауш. Идея период полураспада и возможность предсказания распада была создана на основе их работы.[4]
В 1901 году Роберт Фрэнсис Эрхарт обнаружил неожиданный режим проводимости, исследуя проводимость газов между близко расположенными электродами с помощью Интерферометр Майкельсона. Дж. Дж. Томсон прокомментировал, что находка требует дальнейшего расследования. В 1911, а затем в 1914 году тогдашний аспирант Франц Ротер непосредственно измерил токи установившейся автоэмиссии. Он использовал метод Эрхарта для контроля и измерения расстояния между электродами, но с чувствительной платформой. гальванометр. В 1926 году Ротер измерил токи автоэмиссии в «жестком» вакууме между близко расположенными электродами.[8]
Квантовое туннелирование было впервые замечено в 1927 г. Фридрих Хунд пока он вычислял основное состояние двухъямный потенциал[7] Леонид Мандельштам и Михаил Леонтович открыл его независимо в том же году. Они анализировали последствия тогдашнего нового Волновое уравнение Шредингера.[9]
Его первое приложение было математическим объяснением альфа-распад, который был разработан в 1928 г. Георгий Гамов (кто знал о находках Мандельштама и Леонтовича[10]) и независимо Рональд Герни и Эдвард Кондон.[11][12][13][14] Последние исследователи одновременно решили Уравнение Шредингера для модельного ядерного потенциала и вывели соотношение между период полураспада частицы и энергии излучения, которая напрямую зависит от математической вероятности туннелирования.
Побывав на гамовском семинаре, Макс Борн признал универсальность туннелирования. Он понял, что это не ограничивается ядерная физика, но был общим результатом квантовая механика это относилось ко многим различным системам.[4] Вскоре после этого обе группы рассмотрели случай туннелирования частиц в ядро. Изучение полупроводники и развитие транзисторы и диоды привело к признанию туннелирования электронов в твердых телах к 1957 году. Лео Эсаки, Ивар Гиавер и Брайан Джозефсон предсказал туннелирование сверхпроводящий Куперовские пары, за что получили Нобелевская премия по физике в 1973 г.[4] В 2016 г. квантовое туннелирование воды был открыт.[15]
Введение в концепцию
Квантовое туннелирование подпадает под область квантовая механика: изучение того, что происходит на квантовая шкала. туннелирование нельзя непосредственно воспринимать. Его понимание во многом определяется микроскопическим миром, который классическая механика не могу объяснить. Чтобы понять явление частицы, пытающиеся пересечь потенциальный барьер можно сравнить с мячом, который пытается перекатиться через холм.
Квантовая механика и классическая механика отличаются своим подходом к этому сценарию. Классическая механика предсказывает, что частицы, у которых недостаточно энергии, чтобы классически преодолеть барьер, не могут достичь другой стороны. Таким образом, мяч без энергии, достаточной для преодоления холма, скатится обратно вниз. Мяч, которому не хватает энергии, чтобы пробить стену, отскакивает назад. В качестве альтернативы мяч может стать частью стены (поглощение).
В квантовой механике эти частицы могут с небольшой вероятностью туннель на другую сторону, таким образом пересекая барьер. Мяч в каком-то смысле занимает энергия из окружающей среды пересекает стену. Затем он возвращает энергию, заставляя отраженные электроны[требуется разъяснение ] более энергичным, чем они были бы в противном случае.[16]
Причина этого различия заключается в том, что материя рассматривается как обладающие свойствами волн и частиц. Одна интерпретация этой двойственности включает в себя Принцип неопределенности Гейзенберга, который определяет предел точности позиции и импульс частицы могут быть известны одновременно.[7] Это означает, что ни одно решение не имеет вероятности, равной нулю (или единице), хотя она может приближаться к бесконечности. Если, например, расчет его местоположения был принят как вероятность 1, его скорость должна была бы быть бесконечной (что невозможно). Следовательно, вероятность существования данной частицы на противоположной стороне промежуточного барьера отлична от нуля, и такие частицы будут появляться на «другой» (семантически трудное слово в данном случае) пропорционально этой вероятности.
Проблема туннелирования

В волновая функция частицы суммирует все, что можно знать о физическая система.[17] Поэтому в задачах квантовой механики анализируется волновая функция системы. Используя математические формулировки, такие как Уравнение Шредингера, волновую функцию можно вывести. Площадь абсолютная величина Эта волновая функция напрямую связана с распределением вероятностей положения частицы, которое описывает вероятность того, что частица находится в любом данном месте. Чем шире барьер и выше энергия барьера, тем меньше вероятность туннелирования.
Простая модель туннельного барьера, например прямоугольный барьер, можно анализировать и решать алгебраически. В канонической теории поля туннелирование описывается волновой функцией, имеющей ненулевое значение. амплитуда внутри туннеля; но ток там равен нулю, потому что относительная фаза амплитуды сопряженной волновой функции (производной по времени) равна ортогональный к нему.
Моделирование показывает одну такую систему.

На второй иллюстрации показан принцип неопределенности в действии. Волна ударяется о преграду; барьер заставляет его становиться выше и уже. Волна становится намного более удаленной - теперь она находится по обе стороны от барьера, она шире с каждой стороны и ниже по максимальной амплитуде, но равна общей амплитуде. На обеих иллюстрациях локализация волны в пространстве вызывает локализацию действия барьера во времени, тем самым рассеивая энергию / импульс волны.
Проблемы в реальной жизни часто не имеют, поэтому были разработаны «полуклассические» или «квазиклассические» методы, предлагающие приблизительные решения, такие как Приближение ВКБ. Вероятности могут быть получены с произвольной точностью в зависимости от вычислительных ресурсов с помощью Фейнман с интеграл по путям метод. Такая точность редко требуется в инженерной практике.[нужна цитата ]
Динамическое туннелирование

Концепция квантового туннелирования может быть расширена на ситуации, когда существует квантовый перенос между областями, которые классически не связаны, даже если нет связанного потенциального барьера. Это явление известно как динамическое туннелирование.[18][19].
Туннелирование в фазовом пространстве
Концепция динамического туннелирования особенно подходит для решения проблемы квантового туннелирования в больших измерениях (d> 1). В случае интегрируемая система, где ограниченные классические траектории ограничены тори в фазовое пространство, туннелирование можно понимать как квантовый перенос между полуклассическими состояниями, основанный на двух различных, но симметричных торах.[20]
Туннелирование с помощью хаоса

В реальной жизни большинство систем не интегрируются и демонстрируют различную степень хаоса. Тогда говорят, что классическая динамика является смешанной, а фазовое пространство системы обычно состоит из островов регулярных орбит, окруженных большим морем хаотических орбит. Существование хаотического моря между двумя симметричными торами, где транспорт в классическом смысле разрешен, способствует квантовому туннелированию между ними. Это явление называется туннелированием с помощью хаоса.[21] и характеризуется резкими резонансами скорости туннелирования при изменении любого параметра системы.
Резонансное туннелирование
Когда мала по сравнению с размером регулярных островков, тонкая структура классического фазового пространства играет ключевую роль в туннелировании. В частности, два симметричных тора связаны «через последовательность классически запрещенных переходов через нелинейные резонансы», окружающие два острова. [22].
Связанные явления
Некоторые явления имеют то же поведение, что и квантовое туннелирование, и могут быть точно описаны туннелированием. Примеры включают туннелирование классической ассоциации волна-частица,[23] кратковременная связь волн (применение Волновое уравнение Максвелла к свет ) и применение недисперсионное волновое уравнение от акустика применительно к "волны на струнах". До недавнего времени связь возникающих волн называлась только «туннелированием» в квантовой механике; теперь он используется в других контекстах.
Эти эффекты моделируются аналогично прямоугольный потенциальный барьер. В этих случаях один среда передачи через который волна распространяется это то же самое или почти одинаковое во всем, и вторая среда, через которую волна распространяется по-разному. Это можно описать как тонкую область среды B между двумя областями среды A. Анализ прямоугольный барьер с помощью уравнения Шредингера можно адаптировать к этим другим эффектам при условии, что волновое уравнение имеет бегущая волна решения в среде А, но реальные экспоненциальный растворы в среде B.
В оптика среда A представляет собой вакуум, а среда B - стекло. В акустике среда A может быть жидкостью или газом, а среда B - твердым телом. Для обоих случаев среда A - это область пространства, в которой частицы полная энергия больше, чем его потенциальная энергия среда B - потенциальный барьер. У них есть приходящая волна и результирующие волны в обоих направлениях. Средств и барьеров может быть больше, и барьеры не обязательно должны быть дискретными. В этом случае полезны приближения.
Приложения
Туннелирование является причиной некоторых важных макроскопических физических явлений.
Электроника
Туннелирование - источник утечки тока в очень крупномасштабная интеграция (СБИС) электроники и приводит к значительному потреблению энергии и тепловым эффектам, от которых страдают такие устройства. Это считается нижним пределом того, как можно изготавливать элементы микроэлектроники.[24] туннелирование - это фундаментальный метод, используемый для программирования плавающих ворот флэш-память.
Холодное излучение
Холодное излучение из электроны имеет отношение к полупроводники и сверхпроводник физика. Это похоже на термоэлектронная эмиссия, где электроны случайным образом прыгают с поверхности металла, чтобы следовать за смещением напряжения, потому что они статистически в конечном итоге получают больше энергии, чем барьер, в результате случайных столкновений с другими частицами. Когда электрическое поле очень велико, барьер становится достаточно тонким, чтобы электроны могли туннелировать из атомного состояния, что приводит к току, который изменяется примерно по экспоненте с электрическим полем.[25] Эти материалы важны для флэш-память, электронные лампы, а также некоторые электронные микроскопы.
Туннельный переход
Простой барьер можно создать, разделив два проводника очень тонкой изолятор. Это туннельные переходы, изучение которых требует понимания квантового туннелирования.[26] Джозефсоновские переходы воспользоваться квантовым туннелированием и сверхпроводимостью некоторых полупроводники создать Эффект джозефсона. Это находит применение в прецизионных измерениях напряжений и магнитные поля,[25] так же хорошо как многопереходный солнечный элемент.
Клеточные автоматы с квантовыми точками
QCA представляет собой технологию молекулярно-бинарного логического синтеза, работающую с помощью системы межостровного электронного туннелирования. Это очень маломощное и быстрое устройство, которое может работать на максимальной частоте 15 пГц.[27]
Туннельный диод

Диоды электрические полупроводниковые приборы что позволяет электрический ток течет в одном направлении больше, чем в другом. Устройство зависит от слой истощения между N-тип и Полупроводники P-типа служить своей цели. Когда они сильно легированы, обедненный слой может быть достаточно тонким для туннелирования. Когда применяется небольшое прямое смещение, ток из-за туннелирования становится значительным. Это имеет максимум в точке, где смещение напряжения таков, что уровень энергии p и n зоны проводимости такие же. По мере увеличения напряжения смещения две зоны проводимости больше не совпадают, и диод работает нормально.[28]
Поскольку туннельный ток быстро спадает, могут быть созданы туннельные диоды, которые имеют диапазон напряжений, для которых ток уменьшается с увеличением напряжения. Это особое свойство используется в некоторых приложениях, например, в высокоскоростных устройствах, где характерная вероятность туннелирования изменяется так же быстро, как напряжение смещения.[28]
В резонансный туннельный диод использует квантовое туннелирование совершенно по-другому для достижения аналогичного результата. Этот диод имеет резонансное напряжение, при котором большой ток способствует определенному напряжению, достигаемому путем размещения двух тонких слоев с полосой высокой энергетической проводимости рядом друг с другом. Это создает квантовую потенциальная яма который имеет дискретный самый низкий уровень энергии. Когда этот уровень энергии выше, чем у электронов, туннелирования не происходит, и диод находится в обратном смещении. Когда две энергии напряжения совпадают, электроны текут, как разомкнутый провод. При дальнейшем увеличении напряжения туннелирование становится маловероятным, и диод снова начинает действовать как обычный диод, прежде чем станет заметным второй уровень энергии.[29]
Туннельные полевые транзисторы
Европейский исследовательский проект продемонстрировал полевые транзисторы в котором затвор (канал) управляется посредством квантового туннелирования, а не путем тепловой инжекции, что снижает напряжение затвора с ≈1 вольт до 0,2 вольт и снижает энергопотребление до 100 раз. Если эти транзисторы могут быть увеличены до Микросхемы СБИС, они улучшили бы производительность на каждую мощность интегральные схемы.[30]
Термоядерная реакция
Квантовое туннелирование - важное явление для ядерного синтеза. Температура в ядрах звезд обычно недостаточна для того, чтобы атомные ядра могли преодолеть Кулоновский барьер и достичь Термоядерный синтез. Квантовое туннелирование увеличивает вероятность преодоления этого барьера. Хотя эта вероятность все еще мала, чрезвычайно большого количества ядер в ядре звезды достаточно для поддержания устойчивой реакции синтеза - предварительного условия для эволюции жизни в инсоляционных обитаемых зонах.[31]
Радиоактивный распад
Радиоактивный распад - это процесс испускания частиц и энергии из нестабильного ядра атома с образованием стабильного продукта. Это осуществляется посредством туннелирования частицы из ядра (туннелирование электрона в ядро есть захват электронов ). Это было первое применение квантового туннелирования. Радиоактивный распад - актуальная проблема для астробиология поскольку это следствие квантового туннелирования создает постоянный источник энергии в течение большого интервала времени для сред за пределами околозвездная обитаемая зона где инсоляция была бы невозможна (подземные океаны ) или эффективный.[31]
Астрохимия в межзвездных облаках
Включая квантовое туннелирование, астрохимический синтез различных молекул в межзвездные облака можно объяснить, например, синтез молекулярный водород, воды (лед ) и пребиотик важный формальдегид.[31]
Квантовая биология
Квантовое туннелирование является одним из центральных нетривиальных квантовых эффектов в квантовая биология. Здесь важно и туннелирование электронов, и протонное туннелирование[32] . Электронное туннелирование - ключевой фактор во многих биохимических процессах. окислительно-восстановительные реакции (фотосинтез, клеточное дыхание ), а также ферментативный катализ. Протонное туннелирование - ключевой фактор спонтанного ДНК мутация.[31]
Спонтанная мутация происходит, когда нормальная репликация ДНК происходит после туннелирования особо значимого протона.[33] Водородная связь соединяет пары оснований ДНК. Двухъямный потенциал вдоль водородной связи разделяет потенциальный энергетический барьер. Считается, что потенциал двойной ямы асимметричен, одна яма глубже другой, так что протон обычно находится в более глубокой яме. Чтобы мутация произошла, протон должен проникнуть в более мелкую лунку. Движение протона из его обычного положения называется таутомерный переход. Если в этом состоянии происходит репликация ДНК, правило спаривания оснований для ДНК может быть нарушено, что приведет к мутации.[34] Пер-Олов Лоудин был первым, кто разработал теорию спонтанной мутации в двойная спираль. Считается, что другие случаи мутаций в биологии, вызванные квантовым туннелированием, являются причиной старения и рака.[35]
Квантовая проводимость
В то время Модель Друде из электрическая проводимость делает отличные предсказания о природе электронов, проводящих в металлах, это можно сделать, используя квантовое туннелирование для объяснения природы столкновений электронов.[25] Когда волновой пакет свободного электрона встречает длинный массив равномерно расположенных барьеры отраженная часть волнового пакета равномерно интерферирует с передаваемой между всеми барьерами, так что 100% передача становится возможной. Теория предсказывает, что если положительно заряженные ядра образуют идеально прямоугольный массив, электроны будут туннелировать через металл как свободные электроны, что приведет к чрезвычайно высокой проводимость, и что примеси в металле значительно повредят его.[25]
Сканирующий туннельный микроскоп
Сканирующий туннельный микроскоп (СТМ), изобретенный Герд Бинниг и Генрих Рорер, может позволить отображать отдельные атомы на поверхности материала.[25] Он работает, используя связь между квантовым туннелированием и расстоянием. Когда кончик иглы СТМ приближается к проводящей поверхности, имеющей смещение напряжения, измерение тока электронов, туннелирующих между иглой и поверхностью, показывает расстояние между иглой и поверхностью. Используя пьезоэлектрические стержни которые изменяются в размере при приложении напряжения, высоту наконечника можно регулировать, чтобы туннельный ток оставался постоянным. Изменяющиеся во времени напряжения, которые прикладываются к этим стержням, могут быть записаны и использованы для изображения поверхности проводника.[25] СТМ имеют точность до 0,001 нм, или около 1% атомного диаметра.[29]
Кинетический изотопный эффект
В химическая кинетика, замена света изотоп элемента с более тяжелым обычно приводит к более медленной скорости реакции. Обычно это объясняется различиями в нулевых колебательных энергиях для химических связей, содержащих более легкие и более тяжелые изотопы, и обычно моделируется с использованием теория переходного состояния. Однако в некоторых случаях наблюдаются большие изотопические эффекты, которые нельзя объяснить полуклассическим подходом, и требуется квантовое туннелирование. Р. П. Белл разработал модифицированную трактовку кинетики Аррениуса, которая обычно используется для моделирования этого явления.[36]
Быстрее света
Некоторые физики утверждали, что частицы с нулевым спином могут двигаться быстрее, чем скорость света при туннелировании.[4] Это явно нарушает принцип причинность, так как тогда существует система отсчета, в которой частица прибывает до того, как покинуть ее. В 1998 г. Фрэнсис Э. Лоу кратко рассмотрен феномен туннелирования с нулевым временем.[37] Совсем недавно экспериментальные данные о времени туннелирования фононы, фотоны, и электроны был опубликован Гюнтер Нимц.[38]
Другие физики, такие как Герберт Винфул,[39] оспорила эти требования. Винфул утверждал, что волновой пакет туннелирующей частицы распространяется локально, поэтому частица не может туннелировать через барьер нелокально. Винфул также утверждал, что эксперименты, которые якобы демонстрируют нелокальное распространение, были неправильно истолкованы. В частности, групповая скорость волнового пакета не измеряет его скорость, а связана с количеством времени, в течение которого волновой пакет хранится в барьере. Но проблема остается в том, что волновая функция все еще растет внутри барьера во всех точках одновременно. Другими словами, в любой области, недоступной для измерения, нелокальное распространение все же математически определено.
Математическое обсуждение

Уравнение Шредингера
В не зависящее от времени уравнение Шредингера для одной частицы в одной измерение можно записать как
- или
где
- сокращенный Постоянная Планка,
- m - масса частицы,
- x представляет собой расстояние, измеренное в направлении движения частицы,
- Ψ - волновая функция Шредингера,
- V - это потенциальная энергия частицы (измеряется относительно любого удобного контрольного уровня),
- E - энергия частицы, связанная с движением по оси x (измеренная относительно V),
- M (x) - это величина, определяемая V (x) - E, которая не имеет общепринятого названия в физике.
Решения уравнения Шредингера принимают разные формы для разных значений x, в зависимости от того, положительное или отрицательное значение M (x). Когда M (x) постоянна и отрицательна, то уравнение Шредингера можно записать в виде
Решения этого уравнения представляют собой бегущие волны с фазовой постоянной +k или -k. В качестве альтернативы, если M (x) постоянна и положительна, то уравнение Шредингера можно записать в виде
Решения этого уравнения - возрастающие и убывающие экспоненты в виде мимолетные волны. Когда M (x) изменяется в зависимости от положения, возникает такая же разница в поведении, в зависимости от того, является ли M (x) отрицательным или положительным. Отсюда следует, что знак M (x) определяет природу среды, причем отрицательный M (x) соответствует среде A, а положительный M (x) соответствует среде B. Отсюда следует, что кратковременная связь волн может происходить, если область положительной M (x) зажатой между двумя областями отрицательной M (x), тем самым создавая потенциальный барьер.
Математика рассмотрения ситуации, когда M (x) изменяется в зависимости от x, является сложной, за исключением особых случаев, которые обычно не соответствуют физической реальности. Полная математическая трактовка содержится в монографии Фрёмана и Фрёмана 1965 года. Их идеи не вошли в учебники физики, но их исправления не имеют количественного эффекта.
Приближение ВКБ
Волновая функция выражается как экспонента функции:
- , где
затем разделяется на действительную и мнимую части:
- , где A (x) и B (x) - вещественные функции.
Подставляя второе уравнение в первое и используя тот факт, что мнимая часть должна быть равна 0, получаем:
- .Квантовое туннелирование в формулировка фазового пространства квантовой механики. Функция Вигнера для туннелирования через потенциальный барьер в атомных единицах (а.е.). Сплошные линии представляют набор уровней из Гамильтониан .
Чтобы решить это уравнение с использованием полуклассического приближения, каждую функцию необходимо разложить в виде степенной ряд в . Из уравнений степенной ряд должен начинаться как минимум с порядка чтобы удовлетворить действительную часть уравнения; для хорошего классического предела, начиная с максимальной степени Постоянная Планка возможно предпочтительнее, что приводит к
и
- ,
со следующими ограничениями на условия самого низкого порядка,
и
- .
Здесь можно рассмотреть два крайних случая.
Случай 1Если амплитуда меняется медленно по сравнению с фазой и
- что соответствует классическому движению. Решение следующего порядка расширения дает
Случай 2
- Если фаза изменяется медленно по сравнению с амплитудой, и
- что соответствует туннелированию. Решение следующего порядка расширения дает
В обоих случаях из знаменателя видно, что оба этих приближенных решения плохи вблизи классических точек поворота. . Вдали от потенциального холма частица действует подобно свободной колеблющейся волне; под потенциальным холмом частица претерпевает экспоненциальные изменения амплитуды. Путем рассмотрения поведения в этих пределах и классических поворотных точках может быть принято глобальное решение.
Для начала классический поворотный момент, выбран и расширен в степенной серии о :
Сохранение только члена первого порядка обеспечивает линейность:
- .
Используя это приближение, уравнение вблизи становится дифференциальное уравнение:
- .
Это можно решить с помощью Воздушные функции как решения.
Принимая эти решения для всех классических точек поворота, можно сформировать глобальное решение, которое связывает предельные решения. Учитывая два коэффициента по одну сторону от классической точки поворота, два коэффициента по другую сторону от классической точки поворота можно определить, используя это локальное решение для их соединения.
Следовательно, решения функции Эйри будут асимптотически преобразованы в синус, косинус и экспоненциальные функции в надлежащих пределах. Отношения между и находятся
и
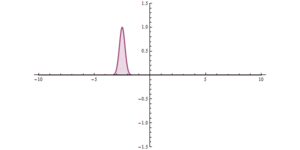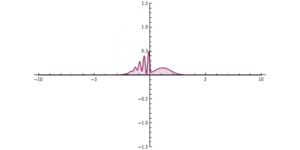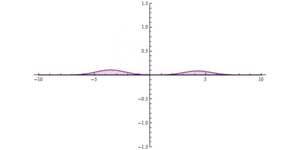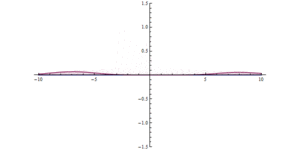 Квантовое туннелирование через барьер. В начале координат (x = 0) существует очень высокий, но узкий потенциальный барьер. Виден значительный туннельный эффект.
Квантовое туннелирование через барьер. В начале координат (x = 0) существует очень высокий, но узкий потенциальный барьер. Виден значительный туннельный эффект.
С найденными коэффициентами можно найти глобальное решение. Следовательно коэффициент передачи для частицы, туннелирующей через единственный потенциальный барьер, равно
- ,
где являются двумя классическими поворотными точками потенциального барьера.
Для прямоугольного барьера это выражение упрощается до:
- .
Смотрите также
- Диэлектрический барьерный разряд
- Автоэлектронная эмиссия
- Метод голштинской селедки
- Протонное туннелирование
- Сверхпроводящий туннельный переход
- Туннельный диод
- Туннельный переход
- Квантовое клонирование
- Белая дыра
использованная литература
- ^ Лернер; Тригг (1991). Энциклопедия физики (2-е изд.). Нью-Йорк: ВЧ. п.1308. ISBN 978-0-89573-752-6.
- ^ Serway; Вюль (2008). Колледж физики. 2 (Восьмое изд.). Бельмонт: Брукс / Коул. ISBN 978-0-495-55475-2.
- ^ Тейлор, Дж. (2004). Современная физика для ученых и инженеров. Прентис Холл. п. 234. ISBN 978-0-13-805715-2.
- ^ а б c d е ж Разавы, Мохсен (2003). Квантовая теория туннелирования. World Scientific. стр.4, 462. ISBN 978-9812564887.
- ^ «Объяснение квантовых компьютеров - пределы человеческих технологий». youtube.com. Kurzgesagt. 8 декабря 2017 г.. Получено 30 декабря 2017.
- ^ «Квантовые эффекты на 7/5 нм и выше». Полупроводниковая техника. Получено 15 июля 2018.
- ^ а б c d Нимц; Хайбель (2008). Нулевое временное пространство. Wiley-VCH. п. 1.
- ^ Томас Кафф. «STM (сканирующий туннельный микроскоп) [забытый вклад Роберта Фрэнсиса Эрхарта в открытие квантового туннелирования]».. ResearchGate.
- ^ Мандельштам, Л .; Леонтович, М. (1928). "Zur Theorie der Schrödingerschen Gleichung". Zeitschrift für Physik. 47 (1–2): 131–136. Bibcode:1928ZPhy ... 47..131M. Дои:10.1007 / BF01391061. S2CID 125101370.
- ^ Файнберг, Э. Л. (2002). «Праотец (о Леониде Исааковиче Мандельштаме)». Успехи физики. 45 (1): 81–100. Bibcode:2002PhyU ... 45 ... 81F. Дои:10.1070 / PU2002v045n01ABEH001126.
- ^ Gurney, R.W .; Кондон, Э. У. (1928). «Квантовая механика и радиоактивный распад». Природа. 122 (3073): 439. Bibcode:1928Натура.122..439Г. Дои:10.1038 / 122439a0. S2CID 4090561.
- ^ Gurney, R.W .; Кондон, Э. У. (1929). «Квантовая механика и радиоактивный распад». Phys. Rev. 33 (2): 127–140. Bibcode:1929ПхРв ... 33..127Г. Дои:10.1103 / PhysRev.33.127.
- ^ Бете, Ганс (27 октября 1966 г.). "Ганс Бете - Сессия I". Библиотека и архив Нильса Бора, Американский институт физики, Колледж-Парк, Мэриленд, США (Интервью). Беседовал Чарльз Вайнер; Джагдиш Мехра. Корнелл Университет. Получено 1 мая 2016.
- ^ Фридлендер, Герхарт; Кеннеди, Джозеф Э .; Миллер, Джулиан Малкольм (1964). Ядерная и радиохимия (2-е изд.). Нью-Йорк: Джон Вили и сыновья. стр.225–7. ISBN 978-0-471-86255-0.
- ^ Колесников, Александр I .; Рейтер, Джордж Ф .; Чоудхури, Нараяни; Приск, Тимоти Р .; Мамонтов, Евгений; Подлесняк Андрей; Элерс, Джордж; Seel, Andrew G .; Весоловски, Дэвид Дж. (2016). «Квантовое туннелирование воды в берилле: новое состояние молекулы воды». Письма с физическими проверками. 116 (16): 167802. Bibcode:2016ПхРвЛ.116п7802К. Дои:10.1103 / PhysRevLett.116.167802. PMID 27152824.
- ^ Дэвис, П. К. У. (2005). «Квантовое время туннелирования» (PDF). Американский журнал физики. 73 (1): 23–27. arXiv:Quant-ph / 0403010. Bibcode:2005AmJPh..73 ... 23D. Дои:10.1119/1.1810153. S2CID 119099861.
- ^ Бьоркен и Дрелл, "Релятивистская квантовая механика", стр. 2. Колледж Макгроу-Хилл, 1965.
- ^ Дэвис, Майкл Дж .; Хеллер, Эрик Дж. (1 июля 1981 г.). «Квантовое динамическое туннелирование в связанных состояниях». Журнал химической физики. 75 (1): 246–254. Bibcode:1981ЖЧФ..75..246Д. Дои:10.1063/1.441832. ISSN 0021-9606.
- ^ Кешавамурти, Шрихари; Шлагек, Питер (9 марта 2011 г.). Динамическое туннелирование: теория и эксперимент. CRC Press. ISBN 978-1-4398-1666-0.
- ^ Уилкинсон, Майкл (1 сентября 1986 г.). «Туннелирование торов в фазовом пространстве». Physica D: нелинейные явления. 21 (2): 341–354. Bibcode:1986ФИД ... 21..341Вт. Дои:10.1016/0167-2789(86)90009-6. ISSN 0167-2789.
- ^ Томсович, Стивен; Ульмо, Денис (1 июля 1994 г.). «Туннелирование с помощью хаоса». Физический обзор E. 50 (1): 145–162. Bibcode:1994PhRvE..50..145T. Дои:10.1103 / PhysRevE.50.145. PMID 9961952.
- ^ Бродье, Оливье; Шлагек, Питер; Ульмо, Денис (25 августа 2002 г.). «Резонансное туннелирование». Анналы физики. 300 (1): 88–136. arXiv:nlin / 0205054. Bibcode:2002AnPhy.300 ... 88B. Дои:10.1006 / aphy.2002.6281. ISSN 0003-4916. S2CID 51895893.
- ^ Эдди, А .; Fort, E .; Moisy, F .; Кудер, Ю. (16 июня 2009 г.). «Непредсказуемое туннелирование классической ассоциации волна-частица» (PDF). Письма с физическими проверками. 102 (24): 240401. Bibcode:2009PhRvL.102x0401E. Дои:10.1103 / PhysRevLett.102.240401. PMID 19658983. Получено 1 мая 2016.
- ^ «Приложения туннелирования» В архиве 23 июля 2011 г. Wayback Machine. Саймон Коннелл 2006.
- ^ а б c d е ж Тейлор, Дж. (2004). Современная физика для ученых и инженеров. Прентис Холл. п. 479. ISBN 978-0-13-805715-2.
- ^ Лернер; Тригг (1991). Энциклопедия физики (2-е изд.). Нью-Йорк: ВЧ. стр.1308–1309. ISBN 978-0-89573-752-6.
- ^ Синха Рой, Судип (25 декабря 2017 г.). Обобщенный квантовый туннельный эффект и окончательные уравнения для времени переключения и приближения рассеяния мощности от ячейки к ячейке в устройствах QCA. Дои:10.13140 / rg.2.2.23039.71849.
- ^ а б Крейн, Кеннет (1983). Современная физика. Нью-Йорк: Джон Уайли и сыновья. п.423. ISBN 978-0-471-07963-7.
- ^ а б Найт, Р. Д. (2004). Физика для ученых и инженеров: с современной физикой. Pearson Education. п. 1311. ISBN 978-0-321-22369-2.
- ^ Ионеску, Адриан М .; Риэль, Хайке (2011). «Туннельные полевые транзисторы как энергоэффективные электронные ключи». Природа. 479 (7373): 329–337. Bibcode:2011Натура.479..329I. Дои:10.1038 / природа10679. PMID 22094693. S2CID 4322368.
- ^ а б c d Трикслер, Ф (2013). «Квантовое туннелирование к происхождению и эволюции жизни». Современная органическая химия. 17 (16): 1758–1770. Дои:10.2174/13852728113179990083. ЧВК 3768233. PMID 24039543.
- ^ Шринивасан, Бхарат (27 сентября 2020 г.). «Совет: обучение кинетике ферментов». Журнал FEBS. Дои:10.1111 / фев.15537. ISSN 1742-464X. PMID 32981225.
- ^ Матта, Шериф Ф. (2014). Квантовая биохимия: электронная структура и биологическая активность. Вайнхайм: Wiley-VCH. ISBN 978-3-527-62922-0.
- ^ Маджумдар, Раби (2011). Квантовая механика: в физике и химии с приложениями к биолоте. Newi: PHI Learning. ISBN 9788120343047.
- ^ Купер, WG (июнь 1993 г.). «Роль эволюции, квантовой механики и точечных мутаций в происхождении рака». Биохимия рака Биофизика. 13 (3): 147–70. PMID 8111728.
- ^ Перси), Белл Р. П. (Рональд (1980). Туннельный эффект в химии. Лондон: Чепмен и Холл. ISBN 0412213400. OCLC 6854792.
- ^ Лоу, Ф. Э. (1998). «Комментарии об очевидном сверхсветовом распространении». Анна. Phys. 7 (7–8): 660–661. Bibcode:1998АнП ... 510..660л. Дои:10.1002 / (SICI) 1521-3889 (199812) 7: 7/8 <660 :: AID-ANDP660> 3.0.CO; 2-0.
- ^ Нимц, Г. (2011). «Туннелирование противостоит специальной теории относительности». Найденный. Phys. 41 (7): 1193–1199. arXiv:1003.3944. Bibcode:2011ФоФ ... 41.1193Н. Дои:10.1007 / s10701-011-9539-2. S2CID 119249900.
- ^ Победоносный, Х. Г. (2006). «Время туннелирования, эффект Хартмана и сверхсветимость: предлагаемое решение старого парадокса». Phys. Rep. 436 (1–2): 1–69. Bibcode:2006PhR ... 436 .... 1Вт. Дои:10.1016 / j.physrep.2006.09.002.
дальнейшее чтение
- Н. Фрёман, П.-О. Фрёман (1965). Приближение JWKB: вклад в теорию. Амстердам: Северная Голландия.
- Разавы, Мохсен (2003). Квантовая теория туннелирования. World Scientific. ISBN 978-981-238-019-7.
- Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Прентис Холл. ISBN 978-0-13-805326-0.
- Джеймс Бинни и Скиннер, Д. (2010). Физика квантовой механики: введение (3-е изд.). Cappella Archive. ISBN 978-1-902918-51-8.
- Либофф, Ричард Л. (2002). Введение в квантовую механику. Эддисон-Уэсли. ISBN 978-0-8053-8714-8.
- Виленкин, Александр; Виленкин, Александр; Виницки, Серж (2003). «Создание частиц в туннельной вселенной». Физический обзор D. 68 (2): 023520. arXiv:gr-qc / 0210034. Bibcode:2003ПхРвД..68б3520Х. Дои:10.1103 / PhysRevD.68.023520. S2CID 118969589.
- H.J.W. Мюллер-Кирстен (2012). Введение в квантовую механику: уравнение Шредингера и интеграл по траекториям, 2-е изд.. Сингапур: World Scientific.























![Psi (x) приблизительно C frac {e ^ {i int dx sqrt { frac {2m} { hbar ^ 2} left (E - V (x) right)} + theta}} { sqrt [4] { frac {2m} { hbar ^ 2} left (E - V (x) right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5ee1989ca3279bca4fb4f1fea48a0c48c724f1e)


![Psi (x) приблизительно frac {C _ {+} e ^ {+ int dx sqrt { frac {2m} { hbar ^ 2} left (V (x) - E right)}} + C _ {-} e ^ {- int dx sqrt { frac {2m} { hbar ^ 2} left (V (x) - E right)}}} { sqrt [4] { frac { 2m} { hbar ^ 2} left (V (x) - E right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4bff4af65fcfda75cb594e31f867ce95e972d22)






![Psi (x) = C_A Ai left ( sqrt [3] {v_1} (x - x_1) right) + C_B Bi left ( sqrt [3] {v_1} (x - x_1) right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/735a1e9ea0d738f9153e0ceab4ef3171c08a6215)





![T (E) = e ^ {{- 2 int _ {{x_ {1}}} ^ {{x_ {2}}} { mathrm {d}} x { sqrt {{ frac {2m} { hbar ^ {2}}} left [V (x) -E right]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/772eea412ba70d586ceb13d18765e61b6d552cbd)

