Комптоновская длина волны - Compton wavelength

В Комптоновская длина волны это квантово-механический собственность частица. Комптоновская длина волны частицы равна длина волны фотона, чей энергия совпадает с массой этой частицы (см. эквивалентность массы и энергии ). Он был представлен Артур Комптон в своем объяснении рассеяния фотоны к электроны (процесс, известный как Комптоновское рассеяние ).

Стандартная комптоновская длина волны, $λ$ , частицы определяется выражением

{ displaystyle lambda = { frac {h} {mc}}, }

в то время как его частота дается,

{ displaystyle f = { frac {mc ^ {2}} {h}}}

куда $час$ это Постоянная Планка, $м$ это частица масса покоя, и $c$ это скорость света. Значение этой формулы показано в вывод формулы комптоновского сдвига.

В CODATA Значение 2018 для комптоновской длины волны электрон является $2.426 31023867 (73) \times 10 -12 м$ .^[1] Другие частицы имеют другие комптоновские длины волн.

Уменьшенная длина волны Комптона

Когда длина волны Комптона делится на $2 π$ , получаем "приведенную" комптоновскую длину волны $ƛ$ (запрещенная лямбда ), т.е.комптоновская длина волны для $1$ радиан вместо $2 π$ радианы:

ƛ = λ / 2 π = час / MC,

куда $час$ это «приведенная» постоянная Планка.

Роль в уравнениях для массивных частиц

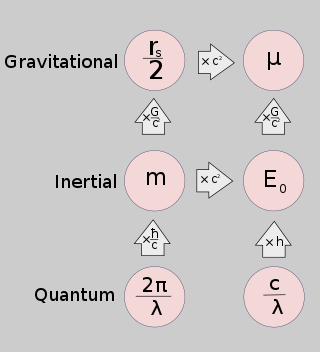
Связь между свойствами массы и соответствующими физическими константами. Считается, что каждый массивный объект обладает всеми пятью свойствами. Однако из-за очень больших или очень маленьких констант, как правило, невозможно проверить более двух или трех свойств для любого объекта.

В Радиус Шварцшильда ( $р s$ ) представляет собой способность массы вызывать искривление пространства и времени.
В стандартный гравитационный параметр ( $μ$ ) представляет собой способность массивного тела воздействовать на другие тела ньютоновскими силами тяготения.
Инерционный масса ( $м$ ) представляет собой ньютоновский отклик массы на силы.
Энергия отдыха ( $E 0$ ) представляет собой способность массы превращаться в другие формы энергии.
В Комптоновская длина волны ( $λ$ ) представляет собой квантовый отклик массы на локальную геометрию.

Обратная приведенная длина волны Комптона является естественным представлением массы на квантовая шкала, и как таковой, он появляется во многих фундаментальных уравнениях квантовой механики. Приведенная комптоновская длина волны появляется в релятивистском Уравнение Клейна – Гордона для свободной частицы:

{ displaystyle mathbf { nabla} ^ {2} psi - { frac {1} {c ^ {2}}} { frac { partial ^ {2}} { partial t ^ {2}} } psi = left ({ frac {mc} { hbar}} right) ^ {2} psi.}

Он появляется в Уравнение Дирака (следующее явно ковариантный форма с использованием Соглашение о суммировании Эйнштейна ):

{ displaystyle -i gamma ^ { mu} partial _ { mu} psi + left ({ frac {mc} { hbar}} right) psi = 0.}

Уменьшенная длина волны Комптона также появляется в Уравнение Шредингера, хотя его присутствие скрыто в традиционных представлениях уравнения. Ниже приводится традиционное представление уравнения Шредингера для электрона в водородоподобный атом:

{ displaystyle i hbar { frac { partial} { partial t}} psi = - { frac { hbar ^ {2}} {2m}} nabla ^ {2} psi - { frac {1} {4 pi epsilon _ {0}}} { frac {Ze ^ {2}} {r}} psi.}

Разделение на ${ displaystyle hbar c}$ , и переписывание с точки зрения постоянная тонкой структуры, получаем:

{ displaystyle { frac {i} {c}} { frac { partial} { partial t}} psi = - { frac {1} {2}} left ({ frac { hbar} {mc}} right) nabla ^ {2} psi - { frac { alpha Z} {r}} psi.}

Различие между уменьшенным и несокращенным

Уменьшенная длина волны Комптона является естественным представлением массы в квантовом масштабе. Уравнения, относящиеся к инертной массе, такие как Клейн-Гордон и Шредингер, используют уменьшенную длину волны Комптона.^[2]^:18–22 Неуменьшенная длина волны Комптона является естественным представлением массы, которая была преобразована в энергию. Уравнения, относящиеся к преобразованию массы в энергию или к длинам волн фотонов, взаимодействующих с массой, используют неуменьшенную длину волны Комптона.

Частица массы $м$ отдыхает энергия $E = MC 2$ Неуменьшенная комптоновская длина волны для этой частицы равна длине волны фотона той же энергии. Для фотонов частота $ж$ , энергия определяется выражением

{ displaystyle E = hf = { frac {hc} { lambda}} = mc ^ {2}, }

что дает неприведенную или стандартную формулу для длины волны Комптона, если она решена для $λ$ .

Ограничение на измерение

Комптоновская длина волны выражает фундаментальное ограничение на измерение положения частицы с учетом квантовая механика и специальная теория относительности.^[3]

Это ограничение зависит от массы $м$ Чтобы увидеть, как это происходит, обратите внимание, что мы можем измерить положение частицы, отражая от нее свет, но для точного измерения положения требуется свет с короткой длиной волны. Свет с короткой длиной волны состоит из фотонов высокой энергии. Если энергия этих фотонов превышает $MC 2$ , при ударе о частицу, положение которой измеряется, столкновение может дать достаточно энергии для создания новой частицы того же типа.^{[нужна цитата ]} Это делает спорным вопрос о местонахождении исходной частицы.

Этот аргумент также показывает, что приведенная длина волны Комптона является порогом, ниже которого квантовая теория поля - который может описывать создание и уничтожение частиц - становится важным. Приведенный выше аргумент можно уточнить следующим образом. Предположим, мы хотим измерить положение частицы с точностью $Δ Икс$ . Тогда отношение неопределенности для должности и импульс Говорит, что

{ displaystyle Delta x , Delta p geq { frac { hbar} {2}},}

так что неопределенность в импульсе частицы удовлетворяет

{ displaystyle Delta p geq { frac { hbar} {2 Delta x}}.}

С использованием релятивистская связь между импульсом и энергией $E 2 = (ПК) 2 + (MC 2) 2$ , когда $Δ п$ превышает $MC$ то неопределенность по энергии больше, чем $MC 2$ , чего достаточно энергия чтобы создать другую частицу того же типа. Но мы должны это исключить. В частности, минимальная неопределенность возникает, когда рассеянный фотон имеет предельную энергию, равную падающей наблюдаемой энергии. Отсюда следует, что существует фундаментальный минимум для $Δ Икс$ :

{ displaystyle Delta x geq { frac {1} {2}} left ({ frac { hbar} {mc}} right).}

Таким образом, неопределенность положения должна быть больше половины приведенной комптоновской длины волны. $час / MC$ .

Комптоновскую длину волны можно противопоставить длина волны де Бройля, который зависит от импульса частицы и определяет границу между поведением частицы и волны в квантовая механика.

Связь с другими константами

Типичные атомные длины, волновые числа и области физики могут быть связаны с уменьшенной комптоновской длиной волны для электрона. ( ${ displaystyle { bar { lambda}} _ { text {e}} Equiv { tfrac { lambda _ { text {e}}} {2 pi}} simeq 386 ~ { textrm { fm}}}$ ) и электромагнитный постоянная тонкой структуры ( ${ displaystyle alpha simeq { tfrac {1} {137}}}$ ).

В Радиус Бора связана с комптоновской длиной волны:

{ displaystyle a_ {0} = { frac {1} { alpha}} left ({ frac { lambda _ { text {e}}} {2 pi}} right) = { frac {{ bar { lambda}} _ { text {e}}} { alpha}} simeq 137 times { bar { lambda}} _ { text {e}} simeq 5.29 times 10 ^ {4} ~ { textrm {fm}}}

В классический радиус электрона примерно в 3 раза больше, чем радиус протона, и написано:

{ displaystyle r _ { text {e}} = alpha left ({ frac { lambda _ { text {e}}} {2 pi}} right) = alpha { bar { lambda }} _ { text {e}} simeq { frac {{ bar { lambda}} _ { text {e}}} {137}} simeq 2.82 ~ { textrm {fm}}}

В Постоянная Ридберга, имеющий размеры линейных волновое число, написано:

{ displaystyle { frac {1} {R _ { infty}}} = { frac {2 lambda _ { text {e}}} { alpha ^ {2}}} simeq 91.1 ~ { textrm {нм}}}

{ displaystyle { frac {1} {2 pi R _ { infty}}} = { frac {2} { alpha ^ {2}}} left ({ frac { lambda _ { text { e}}} {2 pi}} right) = 2 { frac {{ bar { lambda}} _ { text {e}}} { alpha ^ {2}}} simeq 14.5 ~ { textrm {нм}}}

Это дает последовательность:

{ displaystyle r _ { text {e}} = alpha { bar { lambda}} _ { text {e}} = alpha ^ {2} a_ {0} = alpha ^ {3} { гидроразрыв {1} {4 pi R _ { infty}}}}

.

За фермионы, уменьшенная длина волны Комптона задает сечение взаимодействий. Например, сечение для Томсоновское рассеяние фотона от электрона равна^{[требуется разъяснение ]}

{ displaystyle sigma _ {T} = { frac {8 pi} {3}} alpha ^ {2} { bar { lambda}} _ { text {e}} ^ {2} simeq 66.5 ~ { textrm {fm}} ^ {2},}

что примерно такое же, как площадь поперечного сечения ядра железа-56. За измерять бозоны, длина волны Комптона задает эффективный диапазон Юкава взаимодействие: поскольку фотон не имеет массы, электромагнетизм имеет бесконечный диапазон.

В Планковская масса - порядок массы, для которого длина волны Комптона и Радиус Шварцшильда ${ displaystyle r _ { rm {S}} = 2GM / c ^ {2}}$ одинаковы, когда их значение близко к Планковская длина ( ${ displaystyle l _ { rm {P}}}$ ). Радиус Шварцшильда пропорционален массе, тогда как длина волны Комптона пропорциональна обратной массе. Масса и длина Планка определяются:

{ Displaystyle м _ { rm {P}} = { sqrt { hbar c / G}}}

{ displaystyle l _ { rm {P}} = { sqrt { hbar G / c ^ {3}}}.}

внешняя ссылка

Шкалы длины в физике: длина волны Комптона
Б.Г. Сидхарт, От шкалы Планка до шкалы Комптона, Международный институт прикладной математики, Хайдарабад (Индия) и Удине (Италия), август 2006 г.

[1] CODATA 2018 значение для Комптоновская длина волны для электрона из NIST

[2] Грейнер, В., Релятивистская квантовая механика: волновые уравнения (Берлин /Гейдельберг: Springer, 1990), стр. 18–22.

[3] Гарай, Луис Дж. (1995). «Квантовая гравитация и минимальная длина». Международный журнал современной физики A. 10 (2): 145–65. arXiv:gr-qc / 9403008. Bibcode:1995IJMPA..10..145G. Дои:10.1142 / S0217751X95000085.

[1]

[2]

[3]