Радиус Шварцшильда - Schwarzschild radius

Связь между свойствами массы и соответствующими физическими константами. Считается, что каждый массивный объект обладает всеми пятью свойствами. Однако из-за очень больших или очень маленьких констант, как правило, невозможно проверить более двух или трех свойств для любого объекта.

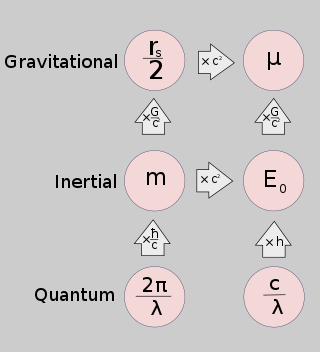
• В Радиус Шварцшильда (р_s) представляет собой способность массы вызывать искривление пространства и времени.
• В стандартный гравитационный параметр (μ) представляет собой способность массивного тела воздействовать на другие тела ньютоновскими силами тяготения.
• Инерционный масса (м) представляет собой ньютоновский отклик массы на силы.
• Энергия отдыха (E₀) представляет собой способность массы превращаться в другие формы энергии.
• В Комптоновская длина волны (λ) представляет собой квантовый отклик массы на локальную геометрию.

В Радиус Шварцшильда (иногда исторически называемый гравитационный радиус) - это физический параметр, который отображается в Решение Шварцшильда к Полевые уравнения Эйнштейна, соответствующий радиус определение горизонт событий Шварцшильда черная дыра. Это характерный радиус, связанный с каждым количеством массы. В Радиус Шварцшильда (Sch. R) был назван в честь Немецкий астроном Карл Шварцшильд, который вычислил это точное решение для теории общая теория относительности в 1916 г.

Радиус Шварцшильда задается как

${ displaystyle r_ {s} = { frac {2GM} {c ^ {2}}},}$

куда грамм это гравитационная постоянная, M - масса объекта, а c это скорость света.^[1]

История

В 1916 г. Карл Шварцшильд получил точное решение^[2][3] уравнениям Эйнштейна для гравитационного поля вне невращающегося сферически-симметричного тела с массой ${ displaystyle M}$ (видеть Метрика Шварцшильда ). Решение содержало термины вида ${ displaystyle 1- {r_ {s}} / r}$ и ${ displaystyle { frac {1} {1- {r_ {s}} / r}}}$, которые стали единственное число в ${ displaystyle r = 0}$ и ${ displaystyle r = r_ {s}}$ соответственно. В ${ displaystyle r_ {s}}$ стал известен как Радиус Шварцшильда. Физическое значение этих особенности обсуждался на протяжении десятилетий. Выяснилось, что на ${ displaystyle r = r_ {s}}$ является координатной сингулярностью, что означает, что это артефакт конкретной системы координат, которая использовалась, в то время как ${ displaystyle r = 0}$ является физическим и не может быть удален.^[4] Радиус Шварцшильда, тем не менее, является физически значимой величиной, как отмечалось выше и ниже.

Это выражение ранее вычислялось с использованием механики Ньютона как радиус сферически симметричного тела, при котором скорость убегания была равна скорости света. Он был идентифицирован в 18 веке Джон Мичелл^[5] и астрономами 19-го века, такими как Пьер-Симон Лаплас.^[6]

Параметры

Радиус Шварцшильда объекта пропорционален массе. Соответственно, солнце имеет радиус Шварцшильда примерно 3,0 км (1,9 мили), тогда как земной шар всего около 9 мм (0,35 дюйма), а Луна составляет около 0,1 мм (0,0039 дюйма). В наблюдаемая вселенная Его масса имеет радиус Шварцшильда примерно 13,7 миллиарда световых лет.^[7][8]

Объект	Масса: ${ displaystyle M}$	Радиус Шварцшильда: ${ displaystyle { frac {2GM} {c ^ {2}}}}$	Плотность Шварцшильда: ${ displaystyle { frac {3c ^ {6}} {32 pi G ^ {3} M ^ {2}}}}$или ${ displaystyle { frac {3c ^ {2}} {8 pi Gr ^ {2}}}}$
Наблюдаемая Вселенная[7]	8.8×1052 кг	1.3×1026 м (13,7 млрд лы )	9.5×10−27 кг / м3
Млечный Путь	1.6×1042 кг	2.4×1015 м (~ 0,25 лы )	0,000029 кг / м3
ТОН 618 (самый большой известная черная дыра )	1.3×1041 кг	1.9×1014 м (~ 1300 Австралия )	0,0045 кг / м3
SMBH в NGC 4889	4.2×1040 кг	6.2×1013 м	0,042 кг / м3
SMBH в Мессье 87[9]	1.3×1040 кг	1.9×1013 м	0,44 кг / м3
SMBH в Галактика Андромеды[10]	3.4×1038 кг	5.0×1011 м	640 кг / м3
Стрелец А * (SMBH в Млечном Пути)	8.2×1036 кг	1.2×1010 м	1.1×106 кг / м3
солнце	1.99×1030 кг	2.95×103 м	1.84×1019 кг / м3
Юпитер	1.90×1027 кг	2,82 метра	2.02×1025 кг / м3
земной шар	5.97×1024 кг	8.87×10−3 м	2.04×1030 кг / м3
Луна	7.35×1022 кг	1.09×10−4 м	1.35×1034 кг / м3
Человек	70 килограмм	1.04×10−25 м	1.49×1076 кг / м3
Биг Мак	0,215 килограмма	3.19×10−28 м	1.58×1081 кг / м3
Планковская масса	2.18×10−8 кг	3.23×10−35 м	1.54×1095 кг / м3

Вывод

Классификация черных дыр по радиусу Шварцшильда

Любой объект, радиус которого меньше его радиуса Шварцшильда, называется черная дыра. Поверхность на радиусе Шварцшильда действует как горизонт событий в невращающемся теле ( вращающаяся черная дыра работает несколько иначе). Ни свет, ни частицы не могут выйти через эту поверхность из области внутри, отсюда и название «черная дыра».

Черные дыры можно классифицировать на основе их радиуса Шварцшильда или, что эквивалентно, по их плотности, где плотность определяется как масса черной дыры, деленная на объем ее сферы Шварцшильда. Поскольку радиус Шварцшильда линейно связан с массой, а замкнутый объем соответствует третьей степени радиуса, поэтому маленькие черные дыры гораздо плотнее больших. Объем, заключенный в горизонте событий самых массивных черных дыр, имеет среднюю плотность ниже, чем у звезд главной последовательности.

Огромная черная дыра

А огромная черная дыра (SMBH) - самый большой тип черной дыры, хотя существует несколько официальных критериев того, как такой объект считается таким, порядка от сотен тысяч до миллиардов солнечных масс. (Сверхмассивные черные дыры размером до 21 миллиарда (2,1 × 10¹⁰) M_☉ были обнаружены, например NGC 4889.)^[11] В отличие от черные дыры звездной массы, сверхмассивные черные дыры имеют сравнительно низкую среднюю плотность. (Обратите внимание, что (невращающаяся) черная дыра - это сферическая область в пространстве, которая окружает сингулярность в ее центре; это не сама сингулярность.) С учетом этого средняя плотность сверхмассивной черной дыры может быть меньше, чем плотность воды.

Радиус Шварцшильда тела пропорционален его массе и, следовательно, его объему, если предположить, что тело имеет постоянную плотность массы.^[12] Напротив, физический радиус тела пропорционален кубическому корню из его объема. Следовательно, по мере того, как тело накапливает материю с заданной фиксированной плотностью (в этом примере 997 кг / м³, плотность воды), его радиус Шварцшильда будет увеличиваться быстрее, чем его физический радиус. Когда тело такой плотности вырастет примерно до 136 миллионов солнечных масс (1,36 × 10⁸) M_☉, его физический радиус превзойдет радиус Шварцшильда, и, таким образом, он образует сверхмассивную черную дыру.

Считается, что подобные сверхмассивные черные дыры не образуются сразу в результате сингулярного коллапса скопления звезд. Вместо этого они могут начать жизнь в виде меньших черных дыр звездных размеров и расти за счет аккреции материи или даже других черных дыр.^{[нужна цитата ]}

Радиус Шварцшильда огромная черная дыра на Галактический Центр составляет примерно 12 миллионов километров.^[13]

Звездная черная дыра

Звездные черные дыры имеют гораздо большую среднюю плотность, чем сверхмассивные черные дыры. Если накапливать материю в ядерная плотность (плотность ядра атома около 10¹⁸ кг / м³; нейтронные звезды также достигают этой плотности), такое скопление попадет в свой собственный радиус Шварцшильда примерно на 3M_☉ и таким образом был бы звездная черная дыра.

Изначальная черная дыра

Небольшая масса имеет чрезвычайно малый радиус Шварцшильда. Масса, подобная гора Эверест^{[14][примечание 1]} имеет радиус Шварцшильда намного меньше, чем нанометр.^{[заметка 2]} Его средняя плотность при таком размере будет настолько высока, что ни один известный механизм не сможет формировать такие чрезвычайно компактные объекты. Такие черные дыры могли образоваться на ранней стадии эволюции Вселенной, сразу после Большой взрыв, когда плотности были чрезвычайно высоки. Поэтому эти гипотетические миниатюрные черные дыры называют изначальные черные дыры.

Другое использование

В гравитационном замедлении времени

Гравитационное замедление времени около большого, медленно вращающегося, почти сферического тела, такого как Земля или Солнце, можно разумно аппроксимировать с помощью радиуса Шварцшильда следующим образом:

${ displaystyle { frac {t_ {r}} {t}} = { sqrt {1 - { frac {r _ { mathrm {s}}} {r}}}}}$

куда:

т_р это время, прошедшее для наблюдателя в радиальной координате р в гравитационном поле;

т - время, прошедшее для наблюдателя, удаленного от массивного объекта (и, следовательно, вне гравитационного поля);

р - радиальная координата наблюдателя (аналогична классическому расстоянию от центра объекта);

р_s - радиус Шварцшильда.

Результаты Эксперимент Паунда – Ребки в 1959 г. оказались совместимыми с предсказаниями общей теории относительности. Измеряя гравитационное замедление времени Земли, этот эксперимент косвенно измерил радиус Земли по Шварцшильду.

В ньютоновских гравитационных полях

Гравитационное поле Ньютона около большого, медленно вращающегося, почти сферического тела можно разумно аппроксимировать с помощью радиуса Шварцшильда следующим образом:

${ displaystyle mg = { frac {GMm} {r ^ {2}}} quad Rightarrow quad gr ^ {2} = GM}$

и

${ displaystyle r _ { mathrm {s}} = { frac {2GM} {c ^ {2}}} quad Rightarrow quad r _ { mathrm {s}} c ^ {2} = 2GM}$

Следовательно, при разделении сверху на нижнее:

${ displaystyle { frac {g} {r _ { mathrm {s}}}} left ({ frac {r} {c}} right) ^ {2} = { frac {1} {2} }}$

куда:

грамм - ускорение свободного падения по радиальной координате р;

р_s - радиус Шварцшильда гравитирующего центрального тела;

р - радиальная координата;

c это скорость света в вакууме.

На поверхности Земли:

${ displaystyle { frac {9.80665 mathrm {m} / mathrm {s} ^ {2}} {8.870056 mathrm {mm}}} left ({ frac {6375416 mathrm {m}}) {299792458 mathrm {m} / mathrm {s}}} right) ^ {2} = left (1105,59 mathrm {s} ^ {- 2} right) left (0,0212661 mathrm { s} right) ^ {2} = { frac {1} {2}}.}$

В кеплеровских орбитах

Для всех круговые орбиты вокруг данного центрального тела:

${ displaystyle { frac {mv ^ {2}} {r}} = { text {Центростремительная сила}} = { text {Гравитационная сила}} = { frac {GMm} {r ^ {2}}} }$

Следовательно,

${ displaystyle rv ^ {2} = GM,}$

но

${ displaystyle r _ { mathrm {s}} c ^ {2} = 2GM}$ (получено выше)

Следовательно,

${ displaystyle { frac {r} {r _ { mathrm {s}}}} left ({ frac {v} {c}} right) ^ {2} = { frac {1} {2} }}$

куда:

р это орбита радиус;

р_s - радиус Шварцшильда гравитирующего центрального тела;

v это орбитальная скорость;

c это скорость света в вакууме.

Это равенство можно обобщить на эллиптические орбиты следующим образом:

${ displaystyle { frac {a} {r _ { mathrm {s}}}} left ({ frac {2 pi a} {cT}} right) ^ {2} = { frac {1} {2}}}$

куда:

а это большая полуось;

Т это орбитальный период.

Для земной шар, как планета, вращающаяся вокруг солнце:

${ displaystyle { frac {1 , mathrm {AU}} {2953.25 , mathrm {m}}} left ({ frac {2 pi , mathrm {AU}} { mathrm {свет , год}}} right) ^ {2} = left (50655379.7 right) left (9.8714403 times 10 ^ {- 9} right) = { frac {1} {2}}.}$

Релятивистские круговые орбиты и фотонная сфера

Уравнение Кеплера для круговых орбит можно обобщить до релятивистского уравнения для круговых орбит, учитывая замедление времени в члене скорости:

${ displaystyle { frac {r} {r_ {s}}} left ({ frac {v} {c}} { sqrt {1 - { frac {r_ {s}} {r}}}}) right) ^ {2} = { frac {1} {2}}}$

${ displaystyle { frac {r} {r_ {s}}} left ({ frac {v} {c}} right) ^ {2} left (1 - { frac {r_ {s}}) {r}} right) = { frac {1} {2}}}$

${ displaystyle left ({ frac {v} {c}} right) ^ {2} left ({ frac {r} {r_ {s}}} - 1 right) = { frac {1 } {2}}.}$

Это последнее уравнение показывает, что объект, вращающийся со скоростью света, будет иметь радиус орбиты в 1,5 раза больше радиуса Шварцшильда. Это особая орбита, известная как фотонная сфера.

Радиус Шварцшильда для массы Планка

Для Планковская масса ${ Displaystyle м _ { rm {P}} = { sqrt { hbar c / G}}}$, радиус Шварцшильда ${ Displaystyle г _ { rm {S}} = 2 ell _ { rm {P}}}$ и Комптоновская длина волны ${ displaystyle lambda _ { rm {C}} = 2 pi ell _ { rm {P}}}$ того же порядка, что и Планковская длина ${ displaystyle ell _ { rm {P}} = { sqrt { hbar G / c ^ {3}}}}$.

Радиус Шварцшильда и принцип неопределенности на планковском масштабе ^[15]

${ displaystyle r_ {s} = { frac {2GM} {c ^ {2}}} = { frac {2G} {c ^ {3}}} Mc = { frac {2G} {c ^ {3 }}} P_ {0} приблизительно { frac {2G} {c ^ {3}}} { frac { hbar} {2r}} = { frac { ell _ {P} ^ {2}} {р}}.}$

Следовательно, ${ displaystyle r_ {s} r sim ell _ {P} ^ {2}}$ или ${ displaystyle Delta r_ {s} Delta r geq ell _ {P} ^ {2}}$

Смотрите также

• Черная дыра, общий обзор
• Предел Чандрасекара, второе требование для образования черной дыры
• Джон Мичелл

Классификация черных дыр по типам:

• Статическая или черная дыра Шварцшильда
• Вращающаяся или керровская черная дыра
• Заряженная черная дыра или черная дыра Ньюмана и черная дыра Керра-Ньюмана

Классификация черных дыр по массе:

• Микро черная дыра и сверхмерная черная дыра
• Планковская длина
• Изначальная черная дыра, гипотетический остаток Большого взрыва
• Звездная черная дыра, которая может быть статической черной дырой или вращающейся черной дырой
• Огромная черная дыра, которая также может быть статической черной дырой или вращающейся черной дырой
• Видимая вселенная, если его плотность равна критическая плотность, как гипотетическая черная дыра
• Виртуальная черная дыра

Примечания

Рекомендации