Омнитусеченный многогранник - Omnitruncated polyhedron

В геометрия, всесторонне усеченный многогранник это усеченный квазирегулярный многогранник. Когда они чередовались, они производят курносые многогранники.

Все усеченные многогранники зоноэдры. У них есть Символ Wythoff p q r | и фигуры вершин в качестве 2р. 2кв. 2р.

В более общем смысле, усеченный многогранник - это скос оператор в Обозначения многогранника Конвея.

Список выпуклых всесторонне усеченных многогранников

Есть три выпуклые формы. Их можно рассматривать как красные грани одного правильного многогранника, желтые или зеленые грани одного правильного многогранника. двойственный многогранник, и синие грани в усеченных вершинах квазирегулярного многогранника.

Wythoff символ p q r \|	Омнитусеченный многогранник	Правильные / квазирегулярные многогранники
3 3 2 \|	Усеченный октаэдр	Тетраэдр /Октаэдр /Тетраэдр
4 3 2 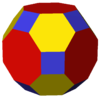\|	Усеченный кубооктаэдр	Куб /Кубооктаэдр /Октаэдр
5 3 2 \|	Усеченный икосододекаэдр	Додекаэдр /Икосододекаэдр /Икосаэдр

Список невыпуклых всесторонне усеченных многогранников

Есть 5 невыпуклая форма всесторонне усеченные многогранники.

Wythoff символ p q r \|	Омнитусеченный звездный многогранник	Wythoff символ p q r \|	Омнитусеченный звездный многогранник
Области прямоугольного треугольника (r = 2)		Общие области треугольников
3 4/3 2 \|	Большой усеченный кубооктаэдр	4 4/3 3 \|	Кубитусеченный кубооктаэдр
3 5/3 2 \|	Большой усеченный икосододекаэдр	5 5/3 3 \|	Икоситроусеченный додекадодекаэдр
5 5/3 2 \|	Усеченный додекадодекаэдр

Другие четные невыпуклые многогранники

Есть 7 невыпуклых форм со смешанными Символы Wythoff p q (r s) |, и в форме галстука-бабочки фигуры вершин, 2р. 2кв.-2кв.-2п. Они не являются настоящими всесторонне усеченными многогранниками: настоящие всестороннеусеченные p q r | или же p q s | совпадают 2р-гональная или 2s-угольные грани соответственно, которые необходимо удалить, чтобы получился правильный многогранник. Все эти многогранники односторонние, т.е. неориентируемый. В p q r | Сначала перечислены вырожденные символы Wythoff, за которыми следуют фактические смешанные символы Wythoff.

Омнитусеченный многогранник	Изображение	Символ Wythoff
Кубогемиоктаэдр		3/2 2 3 \| 2 3 (3/2 3/2) \|
Малый ромбогексаэдр		3/2 2 4 \| 2 4 (3/2 4/2) \|
Большой ромбогексаэдр		4/3 3/2 2 \| 2 4/3 (3/2 4/2) \|
Малый ромбидодекаэдр		2 5/2 5 \| 2 5 (3/2 5/2) \|
Малый додецикосаэдр		3/2 3 5 \| 3 5 (3/2 5/4) \|
Ромбикосаэдр		2 5/2 3 \| 2 3 (5/4 5/2) \|
Большой додецикосаэдр		5/2 5/3 3 \| 3 5/3 (3/2 5/2) \|
Большой ромбидодекаэдр		3/2 5/3 2 \| 2 5/3 (3/2 5/4) \|

Общие омниусечения (скос)

Омнитусечение также называется сокращением или усеченным исправлением (tr), а также оператором скоса Конвея (b). Применительно к нерегулярным многогранникам могут быть созданы новые многогранники, например, эти 2-однородные многогранники:

Coxeter	trrC	trrD	trtT	trtC	trtO	trtI
Конвей	baO	Плохо	btT	btC	btO	btI
Изображение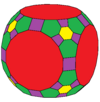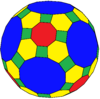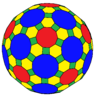

Смотрите также

Равномерный многогранник

Рекомендации

Коксетер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246 (916): 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446, S2CID 202575183
Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
Скиллинг, Дж. (1975), "Полный набор однородных многогранников", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 278 (1278): 111–135, Дои:10.1098 / рста.1975.0022, ISSN 0080-4614, JSTOR 74475, МИСТЕР 0365333, S2CID 122634260
Хар'Эль, З. Равномерное решение для равномерных многогранников., Geometriae Dedicata 47, 57-110, 1993. Цви Хар'Эль, Программное обеспечение Kaleido, Изображений, двойные изображения
Мэдер, Р. Э. Однородные многогранники. Mathematica J. 3, 48-57, 1993.

Операторы многогранников
[
v
т
е
]
Семя	Усечение	Исправление	Bitruncation	Двойной	Расширение	Омнитуркация	Чередования


т₀{p, q} {p, q}	т₀₁{p, q} т {р, д}	т₁{p, q} г {р, д}	т₁₂{p, q} 2t {p, q}	т₂{p, q} 2r {p, q}	т₀₂{p, q} рр {р, q}	т₀₁₂{p, q} tr {p, q}	ht₀{p, q} ч {д, р}	ht₁₂{p, q} s {q, p}	ht₀₁₂{p, q} sr {p, q}