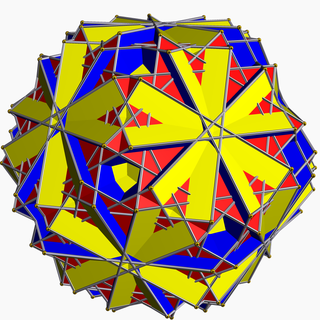
Большой усеченный икосододекаэдр - Great truncated icosidodecahedron
| Большой усеченный икосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 62, E = 180 V = 120 (χ = 2) |
| Лица по сторонам | 30{4}+20{6}+12{10/3} |
| Символ Wythoff | 2 3 5/3 | |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | U68, C87, W108 |
| Двойной многогранник | Большой триаконтаэдр дисьякиса |
| Фигура вершины |  4.6.10/3 |
| Акроним Bowers | Гакватид |

В геометрия, то большой усеченный икосододекаэдр (или же большой квазиусеченный икосододекаэдр или же звездно-усеченный икосододекаэдр) это невыпуклый однородный многогранник, индексируется как U68. Имеет 62 лица (30 квадраты, 20 шестиугольники, и 12 декаграммы ), 180 ребер и 120 вершин.[1] Дается Символ Шлефли т0,1,2{5⁄3, 3} и Диаграмма Кокстера-Дынкина, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Декартовы координаты
Декартовы координаты для вершин большого усеченного икосододекаэдра с центром в начале координат являются все даже перестановки из
- (± τ, ± τ, ± (3−1 / τ)),
- (± 2τ, ± 1 / τ, ± τ−3),
- (± τ, ± 1 / τ2, ± (1 + 3 / τ)),
- (±√5, ±2, ±√5/ τ) и
- (± 1 / τ, ± 3, ± 2 / τ),
где τ = (1+√5) / 2 - это Золотое сечение.
Связанные многогранники
Большой триаконтаэдр дисьякиса
| Большой триаконтаэдр дисьякиса | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо |  |
| Элементы | F = 120, E = 180 V = 62 (χ = 2) |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | DU68 |
| двойственный многогранник | Большой усеченный икосододекаэдр |

В Триаконтаэдр большого дисьякиса (или же трисдьякис икосаэдр) невыпуклый равногранный многогранник. Это двойной большого усеченного икосододекаэдра. Его грани - треугольники.
Пропорции
Треугольники имеют один угол , один из и один из . В двугранный угол равно . Часть каждого треугольника находится внутри твердого тела, поэтому не видна в твердотельных моделях.
Смотрите также
Рекомендации
- ^ Медер, Роман. "68: большой усеченный икосододекаэдр". MathConsult.
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 п. 96
внешняя ссылка
- Вайсштейн, Эрик В. «Большой усеченный икосододекаэдр». MathWorld.
- Вайсштейн, Эрик В. "Большой дисдякис триаконтаэдр". MathWorld.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |




