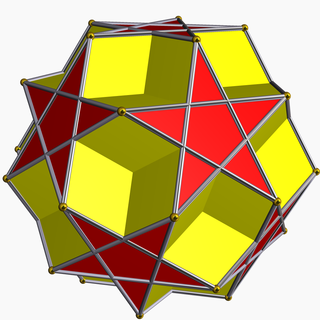
Додекадодекаэдр - Dodecadodecahedron

Додекадодекаэдр
Тип	Равномерный звездный многогранник
Элементы	F = 24, E = 60 V = 30 (χ = −6)
Лица по сторонам	12{5}+12{5/2}
Символ Wythoff	2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4
Группа симметрии	ячас, [5,3], *532
Указатель ссылок	U36, C45, W73
Двойной многогранник	Медиальный ромбический триаконтаэдр
Фигура вершины	5.5/2.5.5/2
Акроним Bowers	Сделал

3D модель додекадодекаэдра

В геометрия, то додекадодекаэдр это невыпуклый однородный многогранник, индексируется как U₃₆.^[1] Это исправление из большой додекаэдр (и его двойственного, малый звездчатый додекаэдр ). Это было независимо открыто Hess  (1878 ), Бадуро (1881 ) и Питч (1882 ).

Края этой модели образуют 10 центральных шестиугольники, и эти, спроецированные на сфера, стать 10 большие круги. Эти 10 вместе с большими окружностями из проекций двух других многогранников образуют 31 большой круг сферического икосаэдра используется в строительстве геодезические купола.

Конструкции Wythoff

В нем четыре Конструкции Wythoff между четырьмя Треугольник Шварца семьи: 2 | 5 5/2, 2 | 5 5/3, 2 | 5/2 5/4, 2 | 5/3 5/4, но представляют идентичные результаты. Аналогичным образом можно дать четыре расширенных Символы Шлефли: r {5 / 2,5}, r {5 / 3,5}, r {5 / 2,5 / 4} и r {5 / 3,5 / 4} или как Диаграммы Кокстера-Дынкина: , , , и .

Сеть

Фигура с таким же внешним видом, что и додекадодекаэдр, может быть построена путем складывания этих сетей:

12 пентаграмм и 20 ромбический кластеры нужны. Однако эта конструкция заменяет пересекающиеся пятиугольные грани додекадодекаэдра непересекающимися наборами ромбов, поэтому она не дает такой же внутренней структуры.

Связанные многогранники

Его выпуклый корпус это икосододекаэдр. Он также разделяет расположение кромок с малый додекагемикосаэдр (имеющий общие пентаграммы лица), и с большой додекагемикосаэдр (имеющий общие пятиугольные грани).

Додекадодекаэдр	Малый додекагемикосаэдр
Большой додекагемикосаэдр	Икосододекаэдр (выпуклый корпус )

Анимированная последовательность усечения от {5/2, 5} до {5, 5/2}

Этот многогранник можно считать исправленный большой додекаэдр. Это центр последовательности усечения между малый звездчатый додекаэдр и большой додекаэдр:

В усеченный маленький звездчатый додекаэдр выглядит как додекаэдр на поверхности, но имеет 24 грани: 12 пятиугольники из усеченных вершин и 12 перекрывающихся как (усеченные пентаграммы). Усечение самого додекадодекаэдра неоднородно, и попытка сделать его однородным приводит к выродиться многогранник (выглядит как малый ромбидодекаэдр с {10/2} многоугольниками, заполняющими додекаэдрический набор отверстий), но он имеет равномерное квазиусечение, усеченный додекадодекаэдр.

Имя	Малый звездчатый додекаэдр	Усеченный малый звездчатый додекаэдр	Додекадодекаэдр	Усеченный здорово додекаэдр	Большой додекаэдр
Кокстер-Дынкин диаграмма
Рисунок

Он топологически эквивалентен факторное пространство из гиперболический Пятиугольная черепица порядка 4, искажая пентаграммы обратно в обычный пятиугольники. Таким образом, это топологически правильный многогранник индекса два:^[2][3]

Цвета на изображении выше соответствуют красным пентаграммам и желтым пятиугольникам додекадодекаэдра в верхней части этой статьи.

Медиальный ромбический триаконтаэдр

Медиальный ромбический триаконтаэдр
Тип	Звездный многогранник
Лицо
Элементы	F = 30, E = 60 V = 24 (χ = −6)
Группа симметрии	ячас, [5,3], *532
Указатель ссылок	DU36
двойственный многогранник	Додекадодекаэдр

В средний ромбический триаконтаэдр невыпуклый равногранный многогранник. Это двойной додекадодекаэдра. Имеет 30 пересекающихся ромбический лица.

Его также можно назвать малым звездчатым триаконтаэдром.

Звездчатость

В средний ромбический триаконтаэдр это звездчатость из ромбический триаконтаэдр, которая является двойственной икосододекаэдру, выпуклой оболочке додекадодекаэдра (двойственной исходному медиальному ромбическому триаконтаэдру).

Связанные гиперболические мозаики

Это топологически эквивалентно фактор-пространству гиперболический квадратная черепица порядка 5, искажая ромбы в квадраты. Таким образом, это топологически правильный многогранник индекса два:^[4]

Обратите внимание, что квадратная мозаика порядка 5 двойственна Пятиугольная черепица порядка 4, а фактор-пространство пятиугольной мозаики порядка 4 топологически эквивалентно двойственному среднему ромбическому триаконтаэдру - додекадодекаэдру.

Смотрите также

• Список равномерных многогранников

Рекомендации

• Бадуро (1881), «Память о равнодушных фигурах», Journal de l'École Polytechnique, 49: 47–172
• Гесс, Эдмунд (1878), Vier archimedeische Polyeder höherer Art, Кассель. Чт. Кей, JFM  10.0346.03
• Питч (1882 г.), "Über halbreguläre Sternpolyheder", Zeitschrift für das Realschulwesen, 7, JFM  14.0448.01
• Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN  978-0-521-54325-5, МИСТЕР  0730208

внешняя ссылка

• Вайсштейн, Эрик В. «Додекадодекаэдр». MathWorld.
• Вайсштейн, Эрик В. «Средний ромбический триаконтаэдр». MathWorld.
• Равномерные многогранники и двойники