Гемиполиэдр - Hemipolyhedron
В геометрия, а гемиполиэдр это равномерный звездный многогранник некоторые лица проходят через его центр. Эти «полукруглые» грани лежат параллельно граням какого-то другого симметричного многогранника, и их количество равно половине числа граней этого другого многогранника - отсюда и префикс «геми».[1]
Приставка «hemi» также используется для обозначения некоторых проективные многогранники, такой как полукуб, которые являются изображением карты 2 к 1 сферический многогранник с центральная симметрия.
Символ Wythoff и фигура вершины
Их Символы Wythoff имеют форму п/(п − q) п/q | р; их фигуры вершин находятся скрещенные четырехугольники. Таким образом, они связаны с канеллированный многогранники, у которых есть похожие символы Wythoff. В конфигурация вершины является п/q.2р.п/(п − q).2р. 2р-угольные грани проходят через центр модели: если они представлены как грани сферические многогранники, они покрывают всю полусферу, а их ребра и вершины лежат вдоль большой круг. В п/(п - q) обозначение подразумевает {п/q} лицо поворачивается назад вокруг фигуры вершины.
Ниже перечислены девять форм с их символами Wythoff и конфигурациями вершин:
 Тетрагемигексаэдр 3/2 3 | 2 (3.4.3/2.4) (п/q = 3, р = 2) |  Октагемиоктаэдр 3/2 3 | 3 (3.6.3/2.6) (п/q = 3, р = 3) |  Малый икосигемидодекаэдр 3/2 3 | 5 (3.10.3/2.10) (п/q = 3, р = 5) |  Большой икосигемидодекаэдр 3/2 3 | 5/3 (3.10/3.3/2.10/3) (п/q = 3, р = 5/3) |  Малый додекагемикосаэдр 5/3 5/2 | 3 (5/2.6.5/3.6) (п/q = 5/2, р = 3) |
 Кубогемиоктаэдр 4/3 4 | 3 (4.6.4/3.6) (п/q = 4, р = 3) |  Малый додекагемидодекаэдр 5/4 5 | 5 (5.10.5/4.10) (п/q = 5, р = 5) |  Большой додекагемидодекаэдр 5/3 5/2 | 5/3 (5/2.10/3.5/3.10/3) (п/q = 5/2, р = 5/3) |  Большой додекагемикосаэдр 5/4 5 | 3 (5.6.5/4.6) (п/q = 5, р = 3) |
Обратите внимание, что калейдоскопическая конструкция Витхоффа генерирует неориентируемые гемиполиэдры (все, кроме октагемиоктаэдра) как двойные покрытия (два совпадающих гемиполиэдра).
На евклидовой плоскости последовательность гемиполиэдров продолжается следующими четырьмя звездными мозаиками, где апейрогоны выглядят как вышеупомянутые экваториальные многоугольники:[нужна цитата ]
| Оригинал исправленный черепица | Край диаграмма | Твердый | Вершина Конфиг | Wythoff | Симметрия |
|---|---|---|---|---|---|
 Квадрат черепица |  |  | 4.∞.4/3.∞ 4.∞.-4.∞ | 4/3 4 | ∞ | p4m |
 Треугольная черепица |  |  | (3.∞.3.∞.3.∞)/2 | 3/2 | 3 ∞ | p6m |
 Трехгексагональный черепица |  |  | 6.∞.6/5.∞ 6.∞.-6.∞ | 6/5 6 | ∞ | |
 | ∞.3.∞.3/2 ∞.3.∞.-3 | 3/2 3 | ∞ |
Из этих четырех плиток только 6/5 6 | ∞ порождается как двойное покрытие конструкцией Витхоффа.
Ориентируемость
Только октагемиоктаэдр представляет собой ориентируемый поверхность; остальные гемиполиэдры имеют неориентируемые или односторонние поверхности.
Двойники гемиполиэдров
Поскольку гемиполиэдры имеют лица проходя через центр, двойные фигуры иметь соответствующие вершины в бесконечности; правильно, на реальная проективная плоскость на бесконечности.[2] В Магнус Веннингер с Двойные модели, они представлены пересекающимися призмы, каждая из которых продолжается в обоих направлениях до одной и той же бесконечно удаленной вершины, чтобы сохранить симметрию. На практике призмы модели обрезаются в удобном для производителя месте. Веннингер предположил, что эти фигуры принадлежат к новому классу людей. звездчатость цифры, называемые звёздчатость до бесконечности. Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.
Таких двойников 9, имеющих только 5 различных внешних форм, четыре из которых существуют в идентичных парах. Члены данной визуально идентичной пары различаются расположением истинных и ложных вершин (ложная вершина - это место, где два ребра пересекаются, но не соединяются). Внешние формы:
 |  |  |  |  |
| Тетрагемигексакрон | Октахемиоктакрон и гексагемиоктакрон | Икосихемидодекакрон малый и малый додекагемидодекакрон | Большой додекагемидодекакрон и великий икосигемидодекакрон | Великий додекагемикосакрон и малый додекагемикосакрон |
| 3 пересекающихся бесконечности квадратные призмы | 4 пересекающихся бесконечности шестиугольные призмы | 6 пересекающихся бесконечных десятиугольные призмы | 6 пересекающихся бесконечных декаграмматические призмы | 10 пересекающихся бесконечных шестиугольные призмы |
Связь с квазирегулярными многогранниками
Гемиполиэдры встречаются парами: огранки из квазирегулярные многогранники с четырьмя гранями в вершине. Эти квазирегулярные многогранники имеют конфигурацию вершин м.п.м.п и их края, помимо формирования м- и п-угольные грани, также образуют полуграни гемиполиэдров. Таким образом, гемиполиэдры могут быть получены из квазирегулярных многогранников, отбрасывая либо м-угольники или п-угольники (для сохранения двух граней на краю), а затем вставка полу-граней. Поскольку либо м-угольники или п-угольники могут быть отброшены, любой из двух гемиполиэдров может быть получен из каждого квазирегулярного многогранника, за исключением октаэдр как тетратраэдр, куда м = п = 3, и две грани конгруэнтны. (Эта конструкция не работает для квазирегулярных многогранников с шестью гранями в вершине, также известных как дитригональные многогранники, так как их ребра не образуют правильных полуграней.)[1]
Поскольку гемиполиэдры, как и квазирегулярные многогранники, также имеют два типа граней, чередующихся вокруг каждой вершины, их иногда также считают квазирегулярными.[1]
| Квазирегулярный многогранник м.п.м.п | Полулики (час-угольники) | Гемиполиэдр с м-гоны выброшены п.час.п/п - 1.час | Гемиполиэдр с п-гоны выброшены м.час.м/м - 1.час |
|---|---|---|---|
 Тетратетраэдр 3.3.3.3 м = 3, п = 3 | 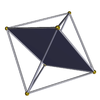 квадраты {4} |  Тетрагемигексаэдр 3.4.3/2.4 |  Тетрагемигексаэдр 3.4.3/2.4 |
 Кубооктаэдр 3.4.3.4 м = 3, п = 4 |  шестиугольники {6} |  Кубогемиоктаэдр 4.6.4/3.6 |  Октагемиоктаэдр 3.6.3/2.6 |
 Икосододекаэдр 3.5.3.5 м = 3, п = 5 |  декагоны {10} |  Малый додекагемидодекаэдр 5.10.5/4.10 |  Малый икосигемидодекаэдр 3.10.3/2.10 |
 Додекадодекаэдр 5.5/2.5.5/2 м = 5, п = 5/2 | 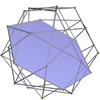 шестиугольники {6} |  Малый додекагемикосаэдр 5/2.6.5/3.6 |  Большой додекагемикосаэдр 5.6.5/4.6 |
 Большой икосододекаэдр 3.5/2.3.5/2 м = 3, п = 5/2 | 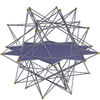 декаграммы {10/3} |  Большой додекагемидодекаэдр 5/2.10/3.5/3.10/3 |  Большой икосигемидодекаэдр 3.10/3.3/2.10/3 |
Здесь м и п соответствуют п/q выше, и час соответствует 2р над.
Рекомендации
- ^ а б c Харт, Джордж (1996). «Квазирегулярные многогранники». Виртуальные многогранники: энциклопедия многогранников. Получено 6 мая 2012.
- ^ (Веннингер 2003, п. 101 )
- Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., Королевское общество, 246 (916): 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446
- Веннингер, Магнус (1974), Модели многогранников, Издательство Кембриджского университета, ISBN 978-0-521-09859-5, МИСТЕР 0467493 (Модели Веннингера: 67, 68, 78, 89, 91, 100, 102, 106, 107)
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN 978-0-521-54325-5, МИСТЕР 0730208
- Хар'Эль, З. Равномерное решение для равномерных многогранников., Geometriae Dedicata 47, 57-110, 1993. Цви Хар'Эль (Стр. 10, 5.2. Полугранники p p '| r.)
внешняя ссылка
- Глоссарий многогранников Stella
- Верси-правильные многогранники в визуальных многогранниках
