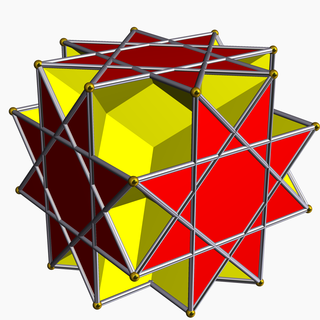
Большой ромбогексаэдр - Great rhombihexahedron

Большой ромбогексаэдр

Тип	Равномерный звездный многогранник
Элементы	F = 18, E = 48 V = 24 (χ = −6)
Лица по сторонам	12{4}+6{8/3}
Символ Wythoff	2 4/3 (3/2 4/2) \|
Группа симметрии	О_час, [4,3], *432
Указатель ссылок	U₂₁, C₈₂, W₁₀₃
Двойной многогранник	Ромбогексакрон большой
Фигура вершины	4.8/3.4/3.8/5
Акроним Bowers	Groh

3D модель большого ромбогексаэдра

В геометрия, то большой ромбогексаэдр (или же большой ромбикуб) это невыпуклый однородный многогранник, индексируется как U₂₁. Имеет 18 граней (12 квадраты и 6 октаграммы ), 48 ребер и 24 вершины.^[1] Его двойной это большой ромбогексакрон.^[2] Его вершина фигуры это скрещенный четырехугольник.

Ортогональные проекции

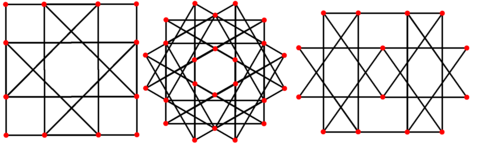
Галерея

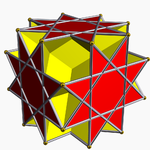Традиционная начинка	Заполнение по модулю-2

Связанные многогранники

Он разделяет расположение вершин с выпуклым усеченный куб. Он также делится своими расположение кромок с невыпуклый большой ромбокубооктаэдр (имеющий 12 общих квадратных граней), и с большой кубокубооктаэдр (имеющий общие октаграммы).

Усеченный куб	Невыпуклый большой ромбокубооктаэдр	Большой кубокубооктаэдр	Большой ромбогексаэдр

Его можно построить как Эксклюзивный или (смесь) из трех восьмиугольные призмы. Точно так же малый ромбогексаэдр могут быть построены как исключительные или из трех восьмиугольные призмы.

Ромбогексакрон большой

Ромбогексакрон большой

Тип	Звездный многогранник
Лицо
Элементы	F = 24, E = 48 V = 18 (χ = −6)
Группа симметрии	О_час, [4,3], *432
Указатель ссылок	DU₂₁
двойственный многогранник	Большой ромбогексаэдр

3D модель большого ромбогексакрона

В большой ромбогексакрон невыпуклый равногранный многогранник. Это двойной из униформа большой ромбогексаэдр (U₂₁).^[3] Имеет 24 одинаковых галстук-бабочка -образный лица, 18 вершины, и 48 края.

Он имеет 12 внешних вершин, которые имеют одинаковые расположение вершин как кубооктаэдр, и 6 внутренних вершин с расположением вершин октаэдр.

Что касается геометрии поверхности, ее можно рассматривать как визуально похожую на Каталонский твердый, то disdyakis додекаэдр, с гораздо более высокими пирамидами, основанными на ромбах, присоединенными к каждой грани ромбический додекаэдр.

Смотрите также

Список равномерных многогранников

внешняя ссылка

Вайсштейн, Эрик В. «Большой ромбогексаэдр». MathWorld.

Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это.

[1] Медер, Роман. "21: большой ромбогексаэдр". MathConsult.

[2] Вайсштейн, Эрик В. "Большой ромбогексаэдр". MathWorld.

[3] Вайсштейн, Эрик В. «Большой ромбогексакрон». MathWorld.

[1]

[2]

[3]