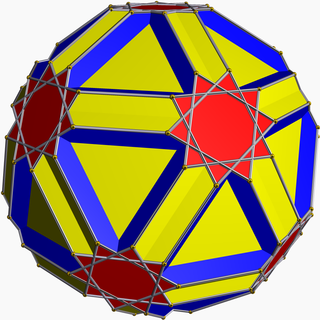
Икоситроусеченный додекадодекаэдр - Icositruncated dodecadodecahedron

Икоситроусеченный додекадодекаэдр
Тип	Равномерный звездный многогранник
Элементы	F = 44, E = 180 V = 120 (χ = −16)
Лица по сторонам	20{6}+12{10}+12{10/3}
Символ Wythoff	3 5 5/3 |
Группа симметрии	ячас, [5,3], *532
Указатель ссылок	U45, C57, W84
Двойной многогранник	Икосаэдр Тридьякиса
Фигура вершины	6.10.10/3
Акроним Bowers	Идтид

Трехмерная модель икосоусеченного додекадодекаэдра

В геометрия, то усеченный додекадодекаэдр или же усеченный икосододекаэдр это невыпуклый однородный многогранник, индексируется как U₄₅.

Выпуклый корпус

Его выпуклый корпус является неоднородным усеченный икосододекаэдр.

Усеченный икосододекаэдр

Выпуклый корпус

Икоситроусеченный додекадодекаэдр

Декартовы координаты

Декартовы координаты для вершин икосоусеченного додекадодекаэдра - все четные перестановки

(± (2−1 / τ), ± 1, ± (2 + τ))

(± 1, ± 1 / τ², ± (3τ − 1))

(± 2, ± 2 / τ, ± 2τ)

(± 3, ± 1 / τ², ± τ²)

(± τ², ± 1, ± (3τ − 2))

где τ = (1+√5) / 2 - это Золотое сечение (иногда пишется φ).

Связанные многогранники

Икосаэдр Тридьякиса

Икосаэдр Тридьякиса
Тип	Звездный многогранник
Лицо
Элементы	F = 120, E = 180 V = 44 (χ = −16)
Группа симметрии	ячас, [5,3], *532
Указатель ссылок	DU45
двойственный многогранник	Икоситроусеченный додекадодекаэдр

В икосаэдр тридьякиса это двойственный многогранник икосоусеченного додекадодекаэдра. Он имеет 44 вершины, 180 ребер и 120 разносторонних треугольных граней.

Смотрите также

• Каталонский твердый Двойники к выпуклым однородным многогранникам
• Равномерные многогранники
• Список равномерных многогранников

Рекомендации

• Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN  978-0-521-54325-5, МИСТЕР  0730208 Фото на странице 96, конструкция Дормана Люка и звездчатый узор на странице 97.

внешняя ссылка

• Вайсштейн, Эрик В. «Икоситроусеченный додекадодекаэдр». MathWorld.

Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это.