Тетраэдрически уменьшенный додекаэдр - Tetrahedrally diminished dodecahedron
| Самодуальная форма Дормана Люка | |
|---|---|
 | |
| Тетраэдрически звездчатый икосаэдр | |
 | |
| Тетраэдрически уменьшенный додекаэдр | |
 | |
| Обозначения многогранника Конвея | pT |
| Лица | 16: 4 {3} + 12 четырехугольники |
| Края | 30 |
| Вершины | 16 |
| Конфигурация вершины | 3.4.4.4 4.4.4 |
| Группа симметрии | Т, [3,3]+, (332), порядок 12 |
| Двойной многогранник | Самодвойственный |
| Характеристики | выпуклый |
   Сети | |
В геометрия, а тетраэдрически уменьшенный[1] додекаэдр (также тетраэдрически звездчатый икосаэдр или же пропелло тетраэдр[2]) представляет собой топологически самодвойственный многогранник, состоящий из 16 вершин, 30 ребер и 16 граней (4 равносторонних треугольника и 12 одинаковых четырехугольников).[3]
Существует каноническая форма с двумя длинами ребер 0,849: 1,057, предполагая, что радиус средняя сфера равно 1. Воздушные змеи остаются равнобедренными.
Имеет хиральный тетраэдрическая симметрия, и поэтому его геометрия может быть построена из пиритоэдрическая симметрия из псевдоикосаэдр с 4 лицами звездчатый, или из пиритоэдр, с 4 вершинами уменьшился. В рамках своего тетраэдрическая симметрия, имеет геометрические разнообразные пропорции. К Дорман Люк двойная конструкция, можно определить уникальную геометрическую пропорцию. У граней кайта отношение длин ребер ~ 1: 0,633.
Топологически треугольники всегда равносторонние, а четырехугольники неправильные, хотя два смежных ребра, пересекающихся в вершинах тетраэдра, равны.
Как самодвойственный гексадекаэдр, это одна из 302404 форм, 1476 с симметрией не менее 2-го порядка и единственная с тетраэдрической симметрией.[4]
Как уменьшился правильный додекаэдр с удаленными 4 вершинами грани четырехугольника трапеции.
Как звездчатость из правильный икосаэдр это одна из 32 звёздчатых звезд, имеющих тетраэдрическую симметрию. У него есть воздушные змеи.[5]
В Обозначения многогранника Конвея, его можно представить как pT, применяя Джордж У. Харт пропеллера к обычному тетраэдр.[6]
Связанные многогранники и соты
Этот многогранник представляет собой вершина фигуры из гиперболические однородные соты, то частично уменьшенные икосаэдрические соты, pd {3,5,3}, с 12 пятиугольные антипризмы и 4 додекаэдр клетки встречаются в каждой вершине.
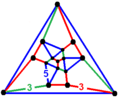
- Фигура вершины спроектирована как Диаграмма Шлегеля
Рекомендации
- ^ Его также менее точно называют тетраэдрически усеченный додекаэдр
- ^ Скульптура на основе пропеллоризированных многогранников
- ^ Тетраэдрически звездчатый икосаэдр
- ^ Самодуальные гексадекаэдры
- ^ Тетраэдрические звёздчатые формы икосаэдра.
- ^ Обозначение Конвея для многогранников
внешняя ссылка
- тетраэдрически усеченный додекаэдр и звездчатый икосаэдр
- Генерация икосаэдра пересечением пяти тетраэдров: геометрические и кристаллографические особенности промежуточных многогранников
- [1] VRML модель в виде усеченного правильного додекаэдра
- [2] Модель VRML в виде тетраэдрически звездчатого икосаэдра

