Граф Гершеля - Herschel graph

Граф Гершеля
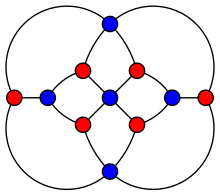Граф Гершеля LS.svg
Граф Гершеля.
Названный в честьАлександр Стюарт Гершель
Вершины11
Края18
Радиус3
Диаметр4
Обхват4
Автоморфизмы12 (D6)
Хроматическое число2
Хроматический индекс4
ХарактеристикиМногогранник
Планарный
Двудольный
Идеально
Таблица графиков и параметров

В теория графов, филиал математика, то Граф Гершеля это двудольный неориентированный граф с 11 вершинами и 18 ребрами, наименьшее негамильтониан многогранник график. Он назван в честь британского астронома. Александр Стюарт Гершель.

Характеристики

Граф Гершеля - это планарный граф: его можно нарисовать в плоскости так, чтобы ни одна из его граней не пересекалась. Это также 3-вершинно-связанный: удаление любых двух его вершин оставляет связную подграф. Это двудольный граф: его вершины можно разделить на два подмножества по пять и шесть вершин соответственно, так что каждое ребро имеет конечную точку в каждом подмножестве (красный и синий подмножества на рисунке) .Как и любой двудольный граф, граф Гершеля является идеальный график : the хроматическое число каждого индуцированный подграф равен размеру самого большого клика этого подграфа. Он также хроматический индекс 4, обхват 4, радиус 3 и диаметр 4.

Многогранник

Граф Гершеля как многогранник.[1] Нажмите здесь, чтобы увидеть анимированную версию.

Граф Гершеля плоский и 3-вершинно-связный, поэтому из него следует Теорема Стейница что это многогранный граф: существует выпуклый многогранник (an эннеэдр ) с графом Гершеля в качестве скелет.[2]У этого многогранника девять четырехугольников для граней, из которых можно образовать три ромбовидные и шесть воздушные змеи.[1]

Его двойственный многогранник это исправленный треугольная призма, образованная как выпуклый корпус середин ребер треугольная призма Этот многогранник обладает тем свойством, что его грани не могут быть пронумерованы таким образом, чтобы последовательные числа появлялись на смежных гранях, а первое и последнее число также находились на смежных гранях. Поскольку многогранная нумерация граней этого типа используется как "вращение вниз счетчики жизни »в игре Магия: Сбор, Константинидес и Константинидес (2018) назовите канонический многогранник реализация этого двойственного многогранника как «Немезида Лича».[3]

Гамильтоничность

Гамильтонов путь (но не цикл) в графе Гершеля

Как двудольный граф с нечетным числом вершин, граф Гершеля не содержит Гамильтонов цикл (цикл ребер, проходящий через каждую вершину ровно один раз). Ведь в любом двудольном графе любой цикл должен чередоваться между вершинами по обе стороны от двудольного графа и, следовательно, должен содержать равное количество вершин обоих типов и иметь четную длину. Таким образом, цикл, проходящий один раз через каждую из одиннадцати вершин, не может существовать в графе Гершеля. Это наименьший негамильтонов многогранный граф, независимо от того, измеряется ли размер графа количеством его вершин, ребер или граней.[4] Существуют и другие многогранные графы с 11 вершинами и без гамильтоновых циклов (особенно График Гольднера – Харари[5]), но с меньшим количеством граней.[2]

Все вершины графа Гершеля, кроме трех, имеют степень три. Гипотеза Тэйта[6] утверждает, что многогранный граф, в котором каждая вершина имеет степень три должно быть гамильтоновым, но это было опровергнуто, когда В. Т. Тутте предоставили контрпример, гораздо больший График Тутте.[7] Уточнение гипотезы Тейта, Гипотеза Барнетта что всякий двудольный 3-регулярный многогранный граф гамильтонов, остается открытым.[8]

Каждый максимальный планарный граф который не имеет гамильтонова цикла, имеет граф Гершеля как незначительный. Предполагается, что граф Гершеля является одним из трех минорно-минимальных негамильтоновых 3-вершинно-связных графов. Два других - это полный двудольный граф и граф, образованный разделением графа Гершеля и на две симметричные половины разделителями по три вершины, а затем объединить половину из каждого графа.[9]

В медиальный график графа Гершеля является 4-регулярным планарный граф без Гамильтоново разложение. Заштрихованные области соответствуют вершинам основного графа Гершеля.

Граф Гершеля также представляет собой пример многогранного графа, для которого медиальный график не может быть разложен на два гамильтоновых цикла с непересекающимися ребрами. Медиальный граф графа Гершеля представляет собой 4-регулярный график с 18 вершинами, по одной на каждое ребро графа Гершеля; две вершины смежны в медиальном графе, если соответствующие ребра графа Гершеля идут подряд на одной из его граней.[10]это 4-вершинно-связанный и по существу, с 6-гранным соединением, означающее, что для каждого разбиения вершин на два подмножества не менее двух вершин существует не менее шести ребер, пересекающих разбиение.[11]

История

График Гершеля назван в честь британского астронома. Александр Стюарт Гершель, который написал раннюю статью о Уильям Роуэн Гамильтон с икозианская игра: граф Гершеля описывает наименьшее выпуклый многогранник для которого эта игра не имеет решения. Однако в статье Гершеля решения для икозианской игры описаны только на графиках правильный тетраэдр и правильный икосаэдр; он не описывал граф Гершеля.[12]Название «граф Гершеля» впервые появилось в учебнике теории графов. Джон Адриан Бонди и США Р. Мурти, опубликовано в 1976 г.[13] Однако сам график был описан ранее, например, Х. С. М. Коксетер.[2]

Рекомендации

  1. ^ а б Лоусон-Перфект, Кристиан (13 октября 2013 г.), "Эннеэдр для Гершеля", Апериодическое издание, получено 7 декабря 2016
  2. ^ а б c Кокстер, Х. С. М. (1973), Правильные многогранники, Дувр, стр. 8.
  3. ^ Константинидес, Энтони Ф .; Константинидес, Джордж А. (октябрь 2018 г.), "Spindown Polyhedra", Математический вестник, 102 (555): 447–453, Дои:10.1017 / mag.2018.111
  4. ^ Барнетт, Дэвид; Юкович, Эрнест (1970), "Гамильтоновы схемы на 3-многогранниках", Журнал комбинаторной теории, 9 (1): 54–59, Дои:10.1016 / S0021-9800 (70) 80054-0.
  5. ^ Вайсштейн, Эрик В., "График Гольднера-Харари", MathWorld.
  6. ^ Тейт, П. Г. (1884), "Листинг Топология", Философский журнал, 5-я серия, 17: 30–46. Перепечатано в Научные статьи, Vol. II, стр. 85–98.
  7. ^ Тутте, В. Т. (1946), «О гамильтоновых схемах» (PDF), Журнал Лондонского математического общества, 21 (2): 98–101, Дои:10.1112 / jlms / s1-21.2.98.
  8. ^ Самал, Роберт (11 июня 2007 г.), Гипотеза Барнетта, открытый проблемный сад, получено 24 февраля 2011
  9. ^ Дин, Гуоли; Маршалл, Эмили (2018), «Минимальный -связные негамильтоновы графы ", Графы и комбинаторика, 34 (2): 289–312, Дои:10.1007 / s00373-018-1874-z, МИСТЕР  3774453
  10. ^ Bondy, J. A .; Хэггквист Р. (1981), "Гамильтоновы циклы с непересекающимися ребрами в 4-регулярных плоских графах", Aequationes Mathematicae, 22 (1): 42–45, Дои:10.1007 / BF02190157.
  11. ^ Кирали, Чаба; Петерфальви, Ференц (2012), "Сбалансированные общие схемы без длинных путей", Дискретная математика, 312 (15): 2262–2271, Дои:10.1016 / j.disc.2012.03.031, МИСТЕР  2926099
  12. ^ Гершель, А.С. (1862), "Икозианская игра сэра У. Гамильтона", Ежеквартальный журнал чистой и прикладной математики, 5: 305.
  13. ^ Бонди, Дж. А.; Мурти, США. (1976), Теория графов с приложениями, Северная Голландия, стр. 53, МИСТЕР  0411988

внешняя ссылка