График Тутте - Википедия - Tutte graph
| График Тутте | |
|---|---|
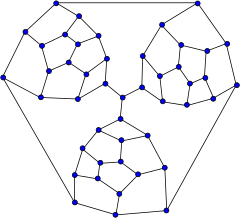 График Тутте | |
| Названный в честь | В. Т. Тутте |
| Вершины | 46 |
| Края | 69 |
| Радиус | 5 |
| Диаметр | 8 |
| Обхват | 4 |
| Автоморфизмы | 3 (Z/3Z) |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Характеристики | Кубический Планарный Многогранник |
| Таблица графиков и параметров | |
в математический поле теория графов, то График Тутте это 3-регулярный граф с 46 вершинами и 69 ребрами, названными в честь В. Т. Тутте.[1] Она имеет хроматическое число 3, хроматический индекс 3, обхват 4 и диаметр 8.
Граф Тутте - это кубический многогранный граф, но негамильтониан. Следовательно, это контрпример к Гипотеза Тэйта что каждый 3-правильный многогранник имеет гамильтонов цикл.[2]
Опубликованный Тутте в 1946 году, это первый контрпример, построенный для этой гипотезы.[3] Позже были найдены и другие контрпримеры, во многих случаях основанные на Теорема Гринберга.
Строительство

Из небольшого плоского графа, называемого фрагментом Тутте, В. Т. Тутте построил негамильтонов многогранник, сложив три таких фрагмента. «Обязательные» ребра фрагментов, которые должны быть частью любого гамильтонова пути через фрагмент, соединяются в центральной вершине; поскольку любой цикл может использовать только два из этих трех ребер, гамильтонова цикла быть не может.
Полученный граф 3-связный и планарный, так что Теорема Стейница это график многогранника. В нем 25 лиц.
Его можно реализовать геометрически из тетраэдра (грани которого соответствуют четырем большим девятиугольным граням на чертеже, три из которых находятся между парами фрагментов, а четвертая из которых образует внешность) путем умножения усечения трех его вершин. .
Алгебраические свойства
Группа автоморфизмов графа Тутте есть Z/3Z, то циклическая группа порядка 3.
В характеристический многочлен графа Тутте:
Связанные графики
Хотя граф Тутте является первым обнаруженным 3-регулярным негамильтоновым многогранным графом, это не самый маленький такой граф.
В 1965 году Ледерберг основал Граф Барнетта – Босака – Ледерберга на 38 вершинах.[4][5] В 1968 году Гринберг построил дополнительные малые контрпримеры к гипотезе Тейта - графы Гринберга на 42, 44 и 46 вершинах.[6] В 1974 г. Фолкнер и Янгер опубликовали еще два графа - графы Фолкнера – Янгера на 42 и 44 вершинах.[7]
Наконец, Холтон и Маккей показали, что существует ровно шесть 38-вершинных негамильтоновых многогранников, которые имеют нетривиальные трехреберные разрезы. Они образуются заменой двух вершин пятиугольная призма тем же фрагментом, что и в примере Тутте.[8]
Рекомендации
- ^ Вайсштейн, Эрик В. "График Тутте". MathWorld.
- ^ Tait, P.G. (1884), "Листинг" Топология", Философский журнал, 5-я серия, 17: 30–46. Перепечатано в Научные статьи, Vol. II, стр. 85–98.
- ^ Тутте, В. Т. (1946), «О гамильтоновых схемах» (PDF), Журнал Лондонского математического общества, 21 (2): 98–101, Дои:10.1112 / jlms / s1-21.2.98.
- ^ Ледерберг, Дж. "DENDRAL-64: Система для компьютерного построения, перечисления и записи органических молекул в виде древовидных структур и циклических графов. Часть II. Топология циклических графов". Промежуточный отчет для Национального управления по аэронавтике и исследованию космического пространства. Грант НСГ 81-60. 15 декабря 1965 г. [1].
- ^ Вайсштейн, Эрик В. "График Барнетта-Босака-Ледерберга". MathWorld.
- ^ Гринберг, Э. Дж. "Плоские однородные графы степени три без гамильтоновых схем". Латвийская математика. Ежегодник, Издат. Зинатне, Рига 4, 51–58, 1968.
- ^ Фолкнер, Г. Б. и Янгер, Д. Х. «Негамильтоновы кубические плоские отображения». Дискретная математика. 7, 67–74, 1974.
- ^ Холтон, Д. А .; Маккей, Б.Д. (1988), «Наименьшие негамильтоновы 3-связные кубические плоские графы имеют 38 вершин», Журнал комбинаторной теории, серия B, 45 (3): 305–319, Дои:10.1016/0095-8956(88)90075-5.


