Полный двудольный граф - Complete bipartite graph

Полный двудольный граф
Полный двудольный граф с м = 5 и п = 3
Вершины	п + м
Края	мин
Радиус	${ displaystyle left {{ begin {array} {ll} 1 & m = 1 vee n = 1 2 & { text {else}} end {array}} right.}$
Диаметр	${ displaystyle left {{ begin {array} {ll} 1 & m = n = 1 2 & { text {else}} end {array}} right.}$
Обхват	${ displaystyle left {{ begin {array} {ll} infty & m = 1 lor n = 1 4 & { text {else}} end {array}} right.}$
Автоморфизмы	${ displaystyle left {{ begin {array} {ll} 2m! n! & n = m m! n! & { text {else}} end {array}} right.}$
Хроматическое число	2
Хроматический индекс	Максимум{м, п}
Спектр	${ displaystyle left {0 ^ {n + m-2}, ( pm { sqrt {nm}}) ^ {1} right }}$
Обозначение	${ displaystyle K_ {m, n}}$
Таблица графиков и параметров

в математический поле теория графов, а полный двудольный граф или же биклика особый вид двудольный граф где каждый вершина первого набора соединяется с каждой вершиной второго набора.^[1][2]

Сама теория графов обычно начинается с Леонард Эйлер 1736 г. Семь мостов Кенигсберга. Тем не мение, рисунки полных двудольных графов были напечатаны уже в 1669 году в связи с изданием сочинений Рамон Лулль Отредактировано Афанасий Кирхер.^[3][4] Сам Лулль сделал аналогичные рисунки полные графики тремя веками ранее.^[3]

Определение

А полный двудольный граф является графом, вершины которого можно разбить на два подмножества V₁ и V₂ такое, что ни одно ребро не имеет обеих конечных точек в одном и том же подмножестве, и каждое возможное ребро, которое может соединять вершины в разных подмножествах, является частью графа. То есть это двудольный граф (V₁, V₂, E) такое, что для каждых двух вершин v₁ ∈ V₁ и v₂ ∈ V₂, v₁v₂ это край в E. Полный двудольный граф с разбиениями размера |V₁| = м и |V₂| = п, обозначается K_{м, н};^[1][2] каждые два графа с одинаковыми обозначениями изоморфный.

Примеры

В звездные графики K_1,3, K_1,4, K_1,5, и K_1,6.

Полный двудольный граф K_4,7 показывая это Проблема кирпичного завода Турана с 4 хранилищами (желтые точки) и 7 печами (синие точки) требуется 18 переходов (красные точки)

• Для любого k, K_1,k называется звезда.^[2] Все полные двудольные графы, деревья звезды.
  • График K_1,3 называется коготь, и используется для определения графы без когтей.^[5]
• График K_3,3 называется график полезности. Это использование происходит из стандартной математической головоломки, в которой три инженерных сети должны быть связаны с тремя зданиями; невозможно решить без переходов из-за непланарность из K_3,3.^[6]

• Максимальные биклики, найденные как подграфы орграфа отношения, называются концепции. Когда решетка формируется путем взятия встреч и соединений этих подграфов, отношение имеет Решетка индуцированных концепций. Такой вид анализа отношений называется формальный анализ концепции.

Характеристики

Пример К_п,п полные двудольные графы^[7]

K3,3	K4,4	K5,5
3 окраски краев	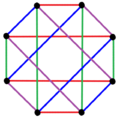4 окраски кромки	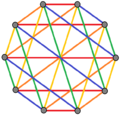5 раскраски кромок
Правильные сложные многоугольники формы 2 {4}п имеют полные двудольные графы с 2п вершины (красный и синий) и п2 2-кромка. Их также можно нарисовать как п окраска краев.

• Для данного двудольного графа проверка, содержит ли он полный двудольный подграф K_я,я для параметрая является НП-полный проблема.^[8]
• А планарный граф не может содержать K_3,3 как незначительный; ан внешнепланарный граф не может содержать K_3,2 как несовершеннолетний (Это не достаточные условия для планарности и внешнепланарности, но необходимо). Наоборот, любой неплоский граф содержит либо K_3,3 или полный график K₅ как несовершеннолетний; это Теорема Вагнера.^[9]
• Каждый полный двудольный граф. K_п,п это Граф Мура и (п,4)-клетка.^[10]
• Полные двудольные графы K_п,п и K_п,п+1 иметь максимально возможное количество ребер среди всех графы без треугольников с таким же количеством вершин; это Теорема Мантеля. Результат Мантеля был обобщен на k-дольные графы и графики, избегающие больших клики как подграфы в Теорема Турана, и эти два полных двудольных графа являются примерами Графики Турана, экстремальные графы для этой более общей задачи.^[11]
• Полный двудольный граф K_м,п имеет число вершинного покрытия из мин{м, п} и номер покрытия края из Максимум{м, п}.
• Полный двудольный граф K_м,п имеет максимальный независимый набор размера Максимум{м, п}.
• В матрица смежности полного двудольного графа K_м,п имеет собственные значения √нм, −√нм и 0; с кратностью 1, 1 и п+м−2 соответственно.^[12]
• В Матрица лапласа полного двудольного графа K_м,п имеет собственные значения п+м, п, м, и 0; с кратностью 1, м−1, п−1 и 1 соответственно.
• Полный двудольный граф K_м,п имеет м^п−1 п^м−1 остовные деревья.^[13]
• Полный двудольный граф K_м,п имеет максимальное соответствие размера мин{м,п}.
• Полный двудольный граф K_п,п имеет надлежащий п-кратная окраска соответствующий Латинский квадрат.^[14]
• Всякий полный двудольный граф является модульный граф: каждая тройка вершин имеет медиану, которая принадлежит кратчайшим путям между каждой парой вершин.^[15]

Смотрите также

• График без биклик, класс разреженных графов, определяемый избеганием полных двудольных подграфов
• Граф короны, граф, образованный удалением идеальное соответствие из полного двудольного графа
• Полный многодольный граф, обобщение полных двудольных графов на более чем два набора вершин
• Бикликовая атака

Рекомендации