Звезда (теория графов) - Star (graph theory)
| Звезда | |
|---|---|
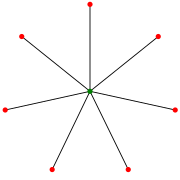 Звезда S7. (Некоторые авторы индексируют это как S8.) | |
| Вершины | к + 1 |
| Края | k |
| Диаметр | минимум (2, k) |
| Обхват | ∞ |
| Хроматическое число | минимум (2, k + 1) |
| Хроматический индекс | k |
| Характеристики | Edge-транзитивный Дерево Единичное расстояние Двудольный |
| Обозначение | Sk |
| Таблица графиков и параметров | |
В теория графов, а звезда Sk это полный двудольный граф K1,k: а дерево с одним внутренним узлом и k листья (но без внутренних узлов и k +1 уходит, когда k ≤ 1). В качестве альтернативы некоторые авторы определяют Sk быть деревом порядок k с максимумом диаметр 2; в этом случае звезда k > 2 имеет k - 1 лист.
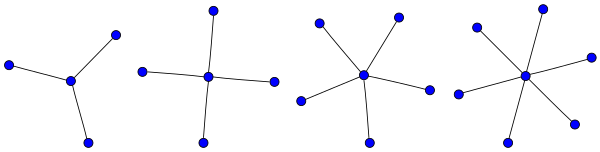
Звезда с 3 ребрами называется коготь.
Звезда Sk является грациозный когда k даже, а не когда k странно. Это ребро-транзитивный график спичек, и имеет диаметр 2 (когда k > 1), обхват ∞ (циклов нет), хроматический индекс k, и хроматическое число 2 (когда k > 0). Кроме того, звезда имеет большую группу автоморфизмов, а именно симметрическую группу из k букв.
Звезды также можно описать как единственные связные графы, в которых не более одной вершины имеет степень больше единицы.
Связь с другими семействами графов
Когти примечательны в определении графы без когтей, графы, не имеющие когтей в качестве индуцированный подграф.[1][2] Они также являются одним из исключительных случаев Теорема об изоморфизме графов Уитни: в общем, графики с изоморфный линейные графики сами изоморфны, за исключением когтя и треугольника K3.[3]
Звезда - это особый вид дерево. Как и любое дерево, звезды могут быть закодированы Последовательность Прюфера; последовательность Прюфера для звезды K1,k состоит из k - 1 копия центральной вершины.[4]
Несколько инварианты графа определены в виде звезд. Звездное древообразование - минимальное количество лесов, на которые можно разбить граф так, чтобы каждое дерево в каждом лесу было звездой,[5] и звездное хроматическое число графа - это минимальное количество цветов, необходимых для раскраски его вершин таким образом, чтобы каждые два класса цветов вместе образовывали подграф, в котором все компоненты связности являются звездами.[6] Графики ширина ответвления 1 - это в точности графики, в которых каждая связная компонента представляет собой звезду.[7]
Другие приложения
Набор расстояний между вершинами когтя представляет собой пример конечного метрическое пространство что не может быть встроено изометрически в Евклидово пространство любого измерения.[8]
В звездная сеть, а компьютерная сеть смоделированный по образцу звездного графика, важен в распределенных вычислений.
Геометрическая реализация звездного графа, образованная отождествлением ребер с интервалами некоторой фиксированной длины, используется в качестве локальной модели кривых в тропическая геометрия. Тропическая кривая определяется как метрическое пространство, локально изоморфное звездному метрическому графу.
Рекомендации
- ^ Фодри, Ральф; Фландрин, Эвелин; Ryjáček, Zdeněk (1997), "Графы без когтей - Обзор", Дискретная математика, 164 (1–3): 87–147, Дои:10.1016 / S0012-365X (96) 00045-3, МИСТЕР 1432221.
- ^ Чудновский, Мария; Сеймур, Пол (2005), "Структура графов без клешней", Обзоры по комбинаторике 2005 г. (PDF), Лондонская математика. Soc. Lecture Note Ser., 327, Кембридж: Cambridge Univ. Press, стр. 153–171, МИСТЕР 2187738.
- ^ Уитни, Хасслер (Январь 1932 г.), «Конгруэнтные графы и связность графов», Американский журнал математики, 54 (1): 150–168, Дои:10.2307/2371086, HDL:10338.dmlcz / 101067, JSTOR 2371086.
- ^ Gottlieb, J .; Julstrom, B.A .; Rothlauf, F .; Райдл, Г. Р. (2001). «Числа Прюфера: плохое представление остовных деревьев для эволюционного поиска» (PDF). GECCO-2001: Труды конференции по генетическим и эволюционным вычислениям. Морган Кауфманн. С. 343–350. ISBN 1558607749.
- ^ Hakimi, S.L .; Mitchem, J .; Шмейхель, Э. Э. (1996), "Звездная древовидность графов", Дискретная математика., 149: 93–98, Дои:10.1016 / 0012-365X (94) 00313-8
- ^ Фертин, Гийом; Распо, Андре; Рид, Брюс (2004), «Звездная раскраска графиков», Журнал теории графов, 47 (3): 163–182, Дои:10.1002 / jgt.20029.
- ^ Робертсон, Нил; Сеймур, Пол Д. (1991), "Миноры графов. X. Препятствия к древовидной декомпозиции", Журнал комбинаторной теории, 52 (2): 153–190, Дои:10.1016 / 0095-8956 (91) 90061-Н.
- ^ Линиал, Натан (2002), «Конечные метрические пространства - комбинаторика, геометрия и алгоритмы», Proc. Международный конгресс математиков, Пекин, 3, стр. 573–586, arXiv:математика / 0304466, Bibcode:2003математика ...... 4466L
