Соединение десяти тетраэдров - Compound of ten tetrahedra
| Соединение десяти тетраэдров | |
|---|---|
 | |
| Тип | регулярное соединение |
| Символ Кокстера | 2{5,3}[10{3,3}]2{3,5}[1] |
| Индекс | UC6, W25 |
| Элементы (Как соединение) | 10 тетраэдры: F = 40, E = 60, V = 20 |
| Двойное соединение | Самодвойственный |
| Группа симметрии | икосаэдр (ячас) |
| Подгруппа ограничиваясь одной составляющей | хиральный четырехгранный (Т) |

В сложный довольно часто тетраэдры является одним из пяти правильных полиэдральных соединений. Этот многогранник можно рассматривать как звездчатость из икосаэдр или сложный. Это соединение было впервые описано Эдмунд Гесс в 1876 г.
Это можно рассматривать как огранка правильного додекаэдра.
Как соединение
Его также можно рассматривать как сложный довольно часто тетраэдры с полная симметрия икосаэдра (ячас). Это одно из пяти обычных соединений, построенных из одинаковых Платоновы тела.
Он разделяет то же самое расположение вершин как додекаэдр.
В соединение пяти тетраэдров представляет собой две хиральные половины этого соединения (поэтому его можно рассматривать как «соединение двух соединений пяти тетраэдров»).
Его можно сделать из соединение пяти кубиков путем замены каждого куба на Stella Octangula на вершинах куба (что приводит к «соединению пяти соединений двух тетраэдров»).
Как звездочка
Этот многогранник это звездчатость из икосаэдр, и задано как Индекс модели Веннингера 25.
| Звездчатая диаграмма | Звездчатость основной | Выпуклый корпус |
|---|---|---|
 | 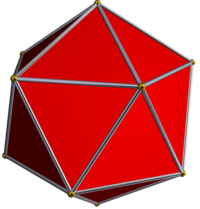 Икосаэдр | 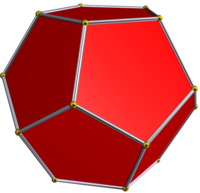 Додекаэдр |
Как грань

Это также огранка из додекаэдр, как показано слева. Вогнутый пентаграммы можно увидеть на соединении, где расположены пятиугольные грани додекаэдра.
Как простой многогранник
Если рассматривать его как простой невыпуклый многогранник без самопересекающихся поверхностей, у него 180 граней (120 треугольников и 60 вогнутых четырехугольников), 122 вершины (60 со степенью 3, 30 со степенью 4, 12 со степенью 5 и 20. со степенью 12) и 300 ребер, что дает Эйлерова характеристика из 122-300 + 180 = +2.
Смотрите также
Рекомендации
- ^ Правильные многогранники, стр.98
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
- Кокстер, Гарольд Скотт Макдональд; Du Val, P .; Flather, H.T .; Петри, Дж. Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквин. ISBN 978-1-899618-32-3. МИСТЕР 0676126. (1-й Эднский университет Торонто (1938))
- H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, 3.6 Пять обычных соединений, стр.47-50, 6.2 Звездчатые тела Платоновых тел, стр.96-104
внешняя ссылка
- Вайсштейн, Эрик В. «Тетраэдр 10-составное». MathWorld.
- VRML модель: [1]
- Соединения 5 и 10 тетраэдров Шандор Кабаи, Демонстрационный проект Wolfram.
- Клитцинг, Ричард. «3D соединение».
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |



















