Соединение пяти октаэдров - Википедия - Compound of five octahedra
| Соединение пяти октаэдров | |
|---|---|
 (см. здесь 3D-модель) | |
| Тип | Обычное соединение |
| Индекс | UC17, Вт23 |
| Символ Кокстера | [5{3,4}]2{3,5}[1] |
| Элементы (Как соединение) | 5 октаэдры: F = 40, E = 60, V = 30 |
| Двойное соединение | Соединение пяти кубиков |
| Группа симметрии | икосаэдр (ячас) |
| Подгруппа ограничиваясь одной составляющей | пиритоэдрический (Тчас) |

В сложный пяти октаэдров является одним из пяти правильных составных многогранников. Этот многогранник можно рассматривать как многогранник звездчатость или сложный. Это соединение было впервые описано Эдмунд Гесс в 1876 году. Он уникален среди обычных соединений тем, что не имеет правильной выпуклой оболочки.
Как звездочка
Это второй звездчатость из икосаэдр, и задано как Индекс модели Веннингера 23.
Его можно построить ромбический триаконтаэдр с ромбической основой пирамиды добавлено ко всем лицам, как показано на пятицветном изображении модели. (Эта конструкция не генерирует обычный соединение пяти октаэдров, но имеет ту же топологию и может плавно деформироваться в правильное соединение.)
Его плотность больше 1.
| Звездчатая диаграмма | Звездчатость основной | Выпуклый корпус |
|---|---|---|
 |  Икосаэдр |  Икосододекаэдр |
Как соединение
Его также можно рассматривать как полиэдрическое соединение из пяти октаэдры организовано в икосаэдрическая симметрия (ячас).
В сферический и стереографический проекции этого соединения выглядят так же, как у дисьякис триаконтаэдр.
Но вершины выпуклого твердого тела на осях 3- и 5-кратной симметрии (серые на изображениях ниже) соответствуют только пересечениям ребер в соединении.
| Сферический многогранник | Стереографические проекции | ||
|---|---|---|---|
| 2-кратный | 3-кратный | 5-кратный | |
 | 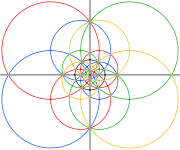 | 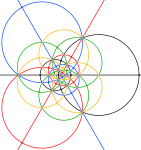 |  |
 |  |  | |
| Область в черных кружках ниже соответствует передней полусфере сферического многогранника. | |||
Замена октаэдров на тетрагемигексаэдры приводит к соединение пяти тетрагемигексаэдров.
Другие 5-октаэдрические соединения
Также существует второе соединение 5-октаэдров с октаэдрической симметрией. Его можно получить, добавив пятый октаэдр к стандартное 4-октаэдрическое соединение.
Смотрите также
- Соединение трех октаэдров
- Соединение четырех октаэдров
- Соединение десяти октаэдров
- Соединение двадцати октаэдров
Рекомендации
- ^ Правильные многогранники, с.49-50, с.98
- Питер Р. Кромвель, Многогранники, Кембридж, 1997.
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
- Коксетер, Гарольд Скотт Макдональд; Du Val, P .; Flather, H.T .; Петри, Дж. Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквин. ISBN 978-1-899618-32-3. МИСТЕР 0676126. (1-й Эднский университет Торонто (1938))
- H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, 3.6 Пять обычных соединений, стр.47-50, 6.2 Звездчатые тела Платоновых тел, стр.96-104
- Э. Гесс 1876 Zugleich Gleicheckigen und Gleichflächigen Polyeder, Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11 (1876), стр. 5–97.
внешняя ссылка
- MathWorld: Octahedron5-составное соединение
- Бумажная модель из пяти октаэдров
- VRML модель: [1][постоянная мертвая ссылка ]
- Клитцинг, Ричард. «3D соединение».
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |


















