Основная теорема теории Галуа - Fundamental theorem of Galois theory

Эта статья не цитировать любой источники. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал без источника может быть оспорен и удаленный. Найдите источники: «Основная теорема теории Галуа»  – Новости  · газеты  · книги  · ученый  · JSTOR (Сентябрь 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В математика, то основная теорема теории Галуа результат, описывающий структуру определенных типов расширения полей в связи с группы. Это было доказано Эварист Галуа в его развитии Теория Галуа.

В своей основной форме теорема утверждает, что с учетом расширения поля E/F то есть конечный и Галуа, Существует индивидуальная переписка между его промежуточными полями и подгруппы своего Группа Галуа. (Промежуточные поля находятся поля K удовлетворение F ⊆ K ⊆ E; их еще называют подрасширения из E/F.)

Подробное описание переписки

Для конечных расширений это соответствие можно явно описать следующим образом.

• Для любой подгруппы ЧАС Гал (E/F) соответствующие фиксированное поле, обозначенный E^ЧАС, это набор этих элементов E которые фиксируются каждым автоморфизм в ЧАС.
• Для любого промежуточного поля K из E/F, соответствующая подгруппа - Aut (E/K), т. е. множество этих автоморфизмов в Gal (E/F), которые фиксируют каждый элемент K.

Основная теорема гласит, что это соответствие является взаимно однозначным, если (и только если) E/F это Расширение Галуа. Например, самое верхнее поле E соответствует тривиальная подгруппа Гал (E/F), а базовое поле F соответствует всему группа Гал (E/F).

Обозначение Gal (E/F) используется только для Расширения Галуа. Если E/F Галуа, то Гал (E/F) = Aut (E/F). Если E/F не Галуа, то "соответствие" дает только инъективный (но нет сюръективный ) карта из ${ displaystyle {{ text {подгруппы Aut}} (E / F) }}$ к ${ displaystyle {{ text {подполя}} E / F }}$, и сюръективное (но не инъективное) отображение в обратном направлении. В частности, если E/F не Галуа, тогда F не является фиксированным полем какой-либо подгруппы Aut (E/F).

Свойства корреспонденции

Соответствие обладает следующими полезными свойствами.

• это включение-реверсирование. Включение подгрупп ЧАС₁ ⊆ ЧАС₂ выполняется тогда и только тогда, когда включение полей E^ЧАС₁ ⊇ E^ЧАС₂ держит.
• Степени расширений связаны с порядками групп способом, соответствующим свойству обращения-включения. В частности, если ЧАС является подгруппой в Gal (E/F), то |ЧАС| = [E:E^ЧАС] и | Gal (E/F)|/|ЧАС| = [E^ЧАС:F].
• Поле E^ЧАС это нормальное расширение из F (или, что то же самое, расширение Галуа, поскольку любое подрасширение сепарабельного расширения сепарабельно) тогда и только тогда, когда ЧАС это нормальная подгруппа Гал (E/F). В этом случае ограничение элементов Gal (E/F) к E^ЧАС вызывает изоморфизм между Гал (E^ЧАС/F) и факторгруппа Гал (E/F)/ЧАС.

Пример 1

Рассмотрим поле

${ Displaystyle К = mathbb {Q} left ({ sqrt {2}}, { sqrt {3}} right) = left [ mathbb {Q} ({ sqrt {2}}) вправо] ({ sqrt {3}}).}$

С K сначала определяется примыканием √2, тогда √3, каждый элемент K можно записать как:

${ displaystyle left (a + b { sqrt {2}} right) + left (c + d { sqrt {2}} right) { sqrt {3}}, qquad a, b, c, d in mathbb {Q}.}$

Его группа Галуа ${ displaystyle G = { text {Gal}} (K / mathbb {Q})}$ можно определить, исследуя автоморфизмы K который исправить а. Каждый такой автоморфизм должен посылать √2 либо √2 или же –√2, и должен отправить √3 либо √3 или же –√3 поскольку перестановки в группе Галуа могут переставлять только корни неприводимого многочлена. Предположим, что ж обмены √2 и –√2, так

${ displaystyle f left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (ab { sqrt {2 }}) + (cd { sqrt {2}}) { sqrt {3}} = ab { sqrt {2}} + c { sqrt {3}} - d { sqrt {6}},}$

и грамм обмены √3 и –√3, так

${ displaystyle g left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (a + b { sqrt {2}}) - (c + d { sqrt {2}}) { sqrt {3}} = a + b { sqrt {2}} - c { sqrt {3}} - d { sqrt {6}}.}$

Очевидно, что это автоморфизмы K. Также существует тождественный автоморфизм е который ничего не меняет, а состав ж и грамм который меняет знаки на обе радикалы:

${ displaystyle (fg) left ((a + b { sqrt {2}}) + (c + d { sqrt {2}}) { sqrt {3}} right) = (ab { sqrt {2}}) - (cd { sqrt {2}}) { sqrt {3}} = ab { sqrt {2}} - c { sqrt {3}} + d { sqrt {6}} .}$

Следовательно,

${ Displaystyle G = left {1, f, g, fg right },}$

и грамм изоморфен Кляйн четыре группы. В нем пять подгрупп, каждая из которых соответствует по теореме подполю поля K.

• Тривиальная подгруппа (содержащая только единичный элемент) соответствует всем K.
• Вся группа грамм соответствует базовому полю ${ displaystyle mathbb {Q}.}$
• Двухэлементная подгруппа {1, ж} соответствует подполю ${ displaystyle mathbb {Q} ({ sqrt {3}}),}$ поскольку ж исправления √3.
• Двухэлементная подгруппа {1, грамм} соответствует подполю ${ displaystyle mathbb {Q} ({ sqrt {2}}),}$ снова с тех пор грамм исправления √2.
• Двухэлементная подгруппа {1, фг} соответствует подполю ${ displaystyle mathbb {Q} ({ sqrt {6}}),}$ поскольку фг исправления √6.

Пример 2

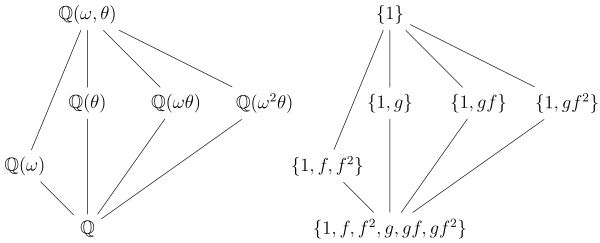
Ниже приводится простейший случай, когда группа Галуа неабелева.

Рассмотрим поле расщепления K полинома ${ displaystyle x ^ {3} -2}$ над ${ Displaystyle mathbb {Q};}$ то есть, ${ Displaystyle К = mathbb {Q} ( omega, theta)}$ где θ - кубический корень из 2, а ω - кубический корень из 1 (но не сам по себе). Например, если мы представим K чтобы быть внутри поля комплексных чисел, мы можем взять θ как действительный кубический корень из 2, а ω как

${ displaystyle omega = { frac {-1} {2}} + i { frac { sqrt {3}} {2}}.}$

Можно показать, что группа Галуа ${ displaystyle G = { text {Gal}} (K / mathbb {Q})}$ имеет шесть элементов и изоморфен группе перестановок трех объектов. Он порождается (например) двумя автоморфизмами, скажем ж и грамм, которые определяются их влиянием на θ и ω,

${ Displaystyle е ( тета) = омега тета, четырехъядерный е ( омега) = омега,}$

${ displaystyle g ( theta) = theta, quad g ( omega) = omega ^ {2},}$

а потом

${ displaystyle G = left {1, f, f ^ {2}, g, gf, gf ^ {2} right }.}$

Подгруппы грамм и соответствующие подполя:

• Как обычно, вся группа грамм соответствует базовому полю ${ displaystyle mathbb {Q}}$ а тривиальная группа {1} соответствует всему полю K.
• Существует единственная подгруппа порядка 3, а именно ${ displaystyle {1, f, f ^ {2} }.}$ Соответствующее подполе ${ Displaystyle mathbb {Q} ( omega),}$ который имеет степень 2 выше ${ displaystyle mathbb {Q}}$ (в минимальный многочлен ω является ${ displaystyle x ^ {2} + x + 1}$), что соответствует тому, что в подгруппе индекс два в грамм. Кроме того, эта подгруппа нормальна, что соответствует тому факту, что подполе нормально над ${ displaystyle mathbb {Q}.}$
• Есть три подгруппы порядка 2, а именно ${ displaystyle {1, g }, {1, gf }}$ и ${ displaystyle {1, gf ^ {2} },}$ соответствующие трем подполям ${ displaystyle mathbb {Q} ( theta), mathbb {Q} ( omega theta), mathbb {Q} ( omega ^ {2} theta).}$ Эти подполя имеют степень 3 выше ${ displaystyle mathbb {Q},}$ опять же соответствующие подгруппам, имеющим индекс 3 в грамм. Обратите внимание, что подгруппы нет нормальный в грамм, и это соответствует тому, что подполя нет Галуа закончился ${ displaystyle mathbb {Q}.}$ Например, ${ Displaystyle mathbb {Q} ( theta)}$ содержит только один корень многочлена ${ displaystyle x ^ {3} -2,}$ так что не может быть нормальный над ${ displaystyle mathbb {Q}.}$

Пример 3

Позволять ${ Displaystyle Е = mathbb {Q} ( lambda)}$ - поле рациональных функций в ${ displaystyle lambda}$ и разреши

${ displaystyle G = left lbrace { lambda, { frac {1} {1- lambda}}, { frac { lambda -1} { lambda}}, { frac {1} { lambda}}, { frac { lambda} { lambda -1}}, 1- lambda} right rbrace subset { rm {Aut}} (E)}$

которая является группой относительно композиции, изоморфной ${ displaystyle S_ {3}}$ (видеть: шесть перекрестных соотношений ).Позволять ${ displaystyle F}$ быть фиксированным полем ${ displaystyle G}$, тогда ${ Displaystyle { rm {Gal}} (E / F) = G}$.

Если ${ displaystyle H}$ является подгруппой ${ displaystyle G}$ то коэффициенты следующего многочлена

${ Displaystyle P (T): = prod _ {h in H} (T-h) in E [T]}$

генерировать фиксированное поле ${ displaystyle H}$. Соответствие Галуа означает, что каждое подполе ${ displaystyle E / F}$ можно построить таким образом. Например, если ${ Displaystyle Н = { лямбда, 1- лямбда }}$ то фиксированное поле ${ Displaystyle mathbb {Q} ( lambda (1- lambda))}$ и если ${ Displaystyle Н = { лямбда, 1 / лямбда }}$ то фиксированное поле ${ Displaystyle mathbb {Q} ( lambda + 1 / lambda)}$. Точно так же можно написать ${ displaystyle F}$, фиксированное поле ${ displaystyle G}$, в качестве ${ displaystyle mathbb {Q} (j),}$ куда j это j-инвариантный.

Подобные примеры можно построить для каждого из группы симметрии платоновых тел поскольку они также добросовестно действуют на проективная линия ${ Displaystyle mathbb {P} ^ {1} ( mathbb {C})}$ и, следовательно, на ${ Displaystyle mathbb {C} (х)}$.

Приложения

Теорема классифицирует промежуточные поля E/F с точки зрения теория групп. Этот перевод между промежуточными полями и подгруппами является ключевым для демонстрации того, что общее квинтическое уравнение не является решаемый радикалами (видеть Теорема Абеля – Руффини ). Сначала определяются группы Галуа радикальные расширения (расширения формы F(α) где α - пкорень -й степени некоторого элемента F), а затем использует основную теорему, чтобы показать, что разрешимые расширения соответствуют разрешимые группы.

Теории, такие как Теория Куммера и теория поля классов основаны на основной теореме.

Бесконечный случай

Учитывая бесконечное алгебраическое расширение, мы все еще можем определить его как Галуа, если оно нормальное и отделимое. Проблема, с которой сталкиваются в бесконечном случае, состоит в том, что биекция в основной теореме не выполняется, поскольку мы обычно получаем слишком много подгрупп. Точнее говоря, если мы просто возьмем каждую подгруппу, мы сможем найти две разные подгруппы, которые фиксируют одно и то же промежуточное поле. Поэтому мы исправляем это, вводя топология о группе Галуа.

Позволять ${ displaystyle E / F}$ - расширение Галуа (возможно бесконечное) и пусть ${ displaystyle G = { text {Gal}} (E / F)}$ - группа Галуа расширения. Позволять

- множество групп Галуа всех конечных промежуточных расширений Галуа. Обратите внимание, что для всех ${ displaystyle i in I}$ мы можем определить карты ${ displaystyle varphi _ {i}: G rightarrow G_ {i}}$ к ${ displaystyle sigma mapsto sigma _ {| L_ {я}}}$. Затем мы определяем Топология Крулля на ${ displaystyle G}$ быть самой слабой топологией, чтобы для всех ${ displaystyle i in I}$ карты ${ displaystyle varphi _ {i}: G rightarrow G_ {i}}$ непрерывны, где мы наделяем каждую ${ displaystyle G_ {i}}$ с дискретной топологией. Говорят иначе ${ Displaystyle G cong varprojlim G_ {i}}$ как обратный предел из топологические группы (где снова каждый ${ displaystyle G_ {i}}$ наделена дискретной топологией). Это делает ${ displaystyle G}$ а проконечная группа (на самом деле каждая проконечная группа может быть реализована как группа Галуа расширения Галуа, см., например, ^[1]). Обратите внимание, что когда ${ displaystyle E / F}$ конечна, топология Крулля - это дискретная топология.

Теперь, когда мы определили топологию группы Галуа, мы можем переформулировать основную теорему для бесконечного расширения Галуа.

Позволять ${ displaystyle { mathcal {F}}}$ обозначим множество всех конечных промежуточных полевых расширений ${ displaystyle E / F}$ и разреши ${ Displaystyle { mathcal {C}}}$ обозначим множество всех замкнутых подгрупп группы ${ displaystyle G = { text {Gal}} (E / F)}$ наделен топологией Крулля. Тогда существует биекция между ${ displaystyle { mathcal {F}}}$ и ${ Displaystyle { mathcal {C}}}$ дано картой

определяется ${ Displaystyle L mapsto { text {Gal}} (E / L)}$ и карта определяется ${ displaystyle N mapsto { text {Fix}} _ {E} (N): = {a in E ~ | ~ sigma (a) = a { text {для всех}} sigma in N }}$. Необходимо проверить одну важную вещь: ${ displaystyle Phi}$ является четко определенной картой, то есть ${ Displaystyle Phi (L)}$ замкнутая подгруппа в ${ displaystyle G}$ для всех промежуточных. Для доказательства см., Например, ^[1]

Рекомендации

внешняя ссылка

• СМИ, связанные с Основная теорема теории Галуа в Wikimedia Commons