Атомная орбиталь - Atomic orbital

В атомная теория и квантовая механика, атомная орбиталь это математическая функция описывающий расположение и волнообразное поведение электрона в атом.[1] Эта функция может использоваться для расчета вероятность найти любой электрон атома в любой конкретной области вокруг ядро атома. Период, термин атомная орбиталь может также относиться к физической области или пространству, где электрон может быть вычислен как присутствующий, как предсказано конкретной математической формой орбитали.[2]
Каждая орбиталь в атоме характеризуется уникальным набором значений трех квантовые числа п, ℓ, и м,[сомнительный ] которые соответственно соответствуют электронным энергия, угловой момент, а угловой момент компонент вектора (в магнитное квантовое число ). Каждая такая орбиталь может быть занята максимум двумя электронами, каждый со своим квантовое число спина s. Простые имена орбитальный, p орбитальный, d орбитальный, и f орбитальный относятся к орбиталям с квантовым числом углового момента ℓ = 0, 1, 2, и 3 соответственно. Эти имена вместе со значениемп, используются для описания электронные конфигурации атомов. Они получены из описания ранними спектроскопистами определенных серий щелочной металл спектроскопические линии в качестве sарфа пrincipal, dесли предохранитель, и жфундаментальный. Орбитали для ℓ > 3 продолжить по алфавиту, опуская j (g, h, i, k, ...)[3][4][5] потому что некоторые языки не различают буквы «i» и «j».[6]
Атомные орбитали - это основные строительные блоки модель атомной орбиты (также известная как модель электронного облака или волновой механики), современная структура для визуализации субмикроскопического поведения электронов в веществе. В этой модели электронное облако многоэлектронного атома можно рассматривать как построенное (в приближении) в электронной конфигурации, которая является продуктом более простого водородоподобный атомные орбитали. Повторяющийся периодичность блоков 2, 6, 10 и 14 элементы в разделах периодическая таблица возникает естественным образом из общего числа электронов, занимающих полный набор s, п, d, и ж атомные орбитали соответственно, хотя для более высоких значений квантового числа п, особенно когда рассматриваемый атом несет положительный заряд, энергии определенных суб-оболочек становятся очень похожими, и поэтому порядок в котором они, как говорят, населены электронами (например, Cr = [Ar] 4s13D5 и Cr2+ = [Ar] 3д4) можно только несколько произвольно рационализировать.

Электронные свойства
С развитием квантовая механика и экспериментальных результатов (таких как дифракция электронов на двух щелях), было обнаружено, что вращающиеся электроны вокруг ядра не могут быть полностью описаны как частицы, но должны быть объяснены волновая дуальность. В этом смысле электроны обладают следующими свойствами:
Волнообразные свойства:
- Электроны не вращаются вокруг ядра, как планета, вращающаяся вокруг Солнца, а вместо этого существуют как стоячие волны. Таким образом, минимально возможная энергия, которую может принять электрон, аналогична основная частота волны на струне. Состояния с более высокой энергией похожи на гармоники этой основной частоты.
- Электроны никогда не находятся в одной точке, хотя вероятность взаимодействия с электроном в одной точке можно определить по волновой функции электрона. Заряд электрона действует так, как будто он размазан в пространстве непрерывным распределением, пропорциональным в любой точке квадрату величины электрона. волновая функция.
Свойства частиц:
- Число электронов, вращающихся вокруг ядра, может быть только целым числом.
- Электроны прыгают между орбиталями, как частицы. Например, если один фотон ударяет по электронам, только один электрон меняет состояние в ответ на фотон.
- Электроны сохраняют свойства частиц, такие как: каждое волновое состояние имеет тот же электрический заряд, что и его электронная частица. Каждое волновое состояние имеет один дискретный спин (спин вверх или вниз) в зависимости от его суперпозиция.
Таким образом, электроны нельзя описать просто как твердые частицы. Можно провести аналогию с большой и часто странной формы «атмосферой» (электроном), распределенной вокруг относительно крошечной планеты (атомного ядра). Атомные орбитали точно описывают форму этой «атмосферы» только тогда, когда в атоме присутствует единственный электрон. Когда к одному атому добавляется больше электронов, дополнительные электроны имеют тенденцию более равномерно заполнять объем пространства вокруг ядра, так что результирующая совокупность (иногда называемая "электронным облаком" атома)[7]) стремится к в целом сферической зоне вероятности, описывающей местоположение электрона, из-за принцип неопределенности.
Формальное квантово-механическое определение
Атомные орбитали можно более точно определить формально. квантово-механический язык. Это приблизительное решение Уравнение Шредингера для электронов, связанных с атомом электрическое поле атома ядро. В частности, в квантовой механике состояние атома, т.е. собственное состояние атомной Гамильтониан, аппроксимируется разложением (см. конфигурационное взаимодействие расширение и базисный набор ) в линейные комбинации антисимметризованных продуктов (Детерминанты Слейтера ) одноэлектронных функций. Пространственные компоненты этих одноэлектронных функций называются атомными орбиталями. (Если учесть также их вращение компонент, о котором говорят атомные спиновые орбитали.) Состояние фактически является функцией координат всех электронов, так что их движение коррелировано, но это часто аппроксимируется следующим образом: модель независимых частиц произведений одноэлектронных волновых функций.[8] (The Лондонская дисперсионная сила, например, зависит от корреляции движения электронов.)
В атомная физика, то атомные спектральные линии соответствуют переходам (квантовые скачки ) между квантовые состояния атома. Эти состояния помечены набором квантовые числа резюмировано в термин символ и обычно связаны с конкретными электронными конфигурациями, то есть схемами заполнения атомных орбиталей (например, 1s2 2 с2 2p6 для основного состояния неон -символ: 1S0).
Это обозначение означает, что соответствующие определители Слейтера имеют явно более высокий вес в конфигурационное взаимодействие расширение. Таким образом, концепция атомной орбиты является ключевой концепцией для визуализации процесса возбуждения, связанного с данным переход. Например, для данного перехода можно сказать, что он соответствует возбуждению электрона с занятой орбитали на данную незанятую орбиталь. Тем не менее, следует иметь в виду, что электроны фермионы управляется Принцип исключения Паули и не отличить друг от друга. Более того, иногда случается, что разложение конфигурационного взаимодействия очень медленно сходится и о простой однодетерминантной волновой функции вообще нельзя говорить. Это тот случай, когда электронная корреляция большой.
По сути, атомная орбиталь - это одноэлектронная волновая функция, хотя большинство электронов не существует в одноэлектронных атомах, и поэтому одноэлектронная точка зрения является приближением. Когда мы думаем об орбиталях, нам часто дают визуализацию орбиты, на которую сильно влияют Хартри – Фок приближение, которое является одним из способов уменьшить сложность теория молекулярных орбиталей.
Типы орбиталей
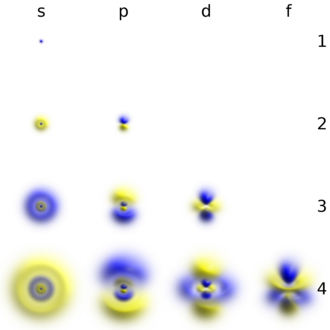
Атомные орбитали могут быть водородоподобными «орбиталями», которые являются точными решениями Уравнение Шредингера для водородоподобный «атом» (т.е. атом с одним электроном). В качестве альтернативы, атомные орбитали относятся к функциям, которые зависят от координат одного электрона (то есть орбитали), но используются в качестве отправных точек для приближения волновых функций, которые зависят от одновременных координат всех электронов в атоме или молекуле. В системы координат выбранные для атомных орбиталей обычно сферические координаты (р, θ, φ) в атомах и картезианцы (х, у, г) в многоатомных молекулах. Преимущество сферических координат (для атомов) состоит в том, что орбитальная волновая функция представляет собой произведение трех факторов, каждый из которых зависит от одной координаты: ψ (р, θ, φ) = р(р) Θ (θ) Φ (φ). Угловые факторы атомных орбиталей Θ (θ) Φ (φ) генерировать функции s, p, d и т. д. как реальные комбинации из сферические гармоники Yℓm(θ, φ) (куда ℓ и м квантовые числа). Обычно существует три математических вида радиальных функцийр(р) который можно выбрать в качестве отправной точки для расчета свойств атомов и молекул с большим количеством электронов:
- В водородоподобные атомные орбитали получены из точного решения уравнения Шредингера для одного электрона и ядра, для водородоподобный атом. Часть функции, зависящая от расстояния р из ядра узлы (радиальные узлы) и распадается как е- (постоянное × расстояние).
- В Орбитальный слейтер-тип (STO) - это форма без радиальных узлов, но распадающаяся из ядра, как и водородоподобная орбиталь.
- Форма Орбиталь гауссовского типа (Гауссианы) не имеет радиальных узлов и распадается как .
Хотя водородоподобные орбитали по-прежнему используются в качестве педагогических инструментов, появление компьютеров сделало STO предпочтительными для атомов и двухатомных молекул, поскольку комбинации STO могут заменить узлы на водородоподобной атомной орбитали. Гауссианы обычно используются в молекулах с тремя или более атомами. Хотя сами по себе они не так точны, как STO, комбинации многих гауссианов могут достичь точности водородоподобных орбиталей.
История
Термин «орбитальный» был введен Роберт Малликен в 1932 г. как сокращение от одноэлектронная орбитальная волновая функция.[9] Однако идея о том, что электроны могут вращаться вокруг компактного ядра с определенным угловым моментом, была убедительно аргументирована, по крайней мере, 19 лет назад: Нильс Бор,[10] и японский физик Хантаро Нагаока опубликовал основанную на орбите гипотезу электронного поведения еще в 1904 году.[11] Объяснение поведения этих электронных "орбит" было одной из движущих сил развития квантовая механика.[12]
Ранние модели
С Дж. Дж. Томсон открытие электрона в 1897 году,[13] Стало ясно, что атомы - не самые маленькие строительные блоки природы, а скорее составные частицы. Недавно открытая структура внутри атомов заставила многих представить, как составные части атома могут взаимодействовать друг с другом. Томсон предположил, что несколько электронов вращаются по орбитальным кольцам внутри положительно заряженного желеобразного вещества,[14] и между открытием электрона и 1909 г. это "сливовый пудинг модель "было наиболее широко распространенным объяснением строения атома.
Вскоре после открытия Томсона Хантаро Нагаока предсказал другую модель электронной структуры.[11] В отличие от модели сливового пудинга, положительный заряд в «Модели Сатурна» Нагаоки был сконцентрирован в центральном ядре, вытягивая электроны по круговым орбитам, напоминающим кольца Сатурна. В то время мало кто обращал внимание на работу Нагаока,[15] и сам Нагаока признал фундаментальный недостаток в теории даже в ее концепции, а именно, что классический заряженный объект не может поддерживать орбитальное движение, потому что он ускоряется и, следовательно, теряет энергию из-за электромагнитного излучения.[16] Тем не менее Сатурнианская модель оказалось, что имеет больше общего с современной теорией, чем любой из ее современников.
Атом Бора
В 1909 г. Эрнест Резерфорд обнаружил, что основная масса атомной массы была плотно конденсирована в ядро, которое также оказалось положительно заряженным. Из его анализа в 1911 году стало ясно, что модель сливового пудинга не может объяснить атомную структуру. В 1913 году аспирант Резерфорда, Нильс Бор, предложила новую модель атома, в которой электроны вращаются вокруг ядра с классическими периодами, но им разрешено иметь только дискретные значения углового момента, квантованные в единицах час/ 2π.[10] Это ограничение автоматически допускало только определенные значения энергии электронов. В Модель Бора атома исправил проблему потери энергии из-за излучения из основного состояния (заявив, что не было состояния ниже этого), и, что более важно, объяснил происхождение спектральных линий.

После использования Бором Эйнштейн объяснение фотоэлектрический эффект связать энергетические уровни в атомах с длиной волны излучаемого света, связь между структурой электронов в атомах и выброс и спектры поглощения атомов становится все более полезным инструментом в понимании электронов в атомах. Наиболее характерной особенностью спектров излучения и поглощения (известных экспериментально с середины XIX века) было то, что эти атомные спектры содержали дискретные линии. Значение модели Бора состояло в том, что она связала линии в спектрах излучения и поглощения с разницей в энергии между орбитами, которые электроны могли перемещать вокруг атома. Однако это было нет достигнутая Бором путем придания электронам некоторых волновых свойств, поскольку идея о том, что электроны могут вести себя как волны материи не было предложено до одиннадцати лет спустя. Тем не менее, использование в модели Бора квантованных угловых моментов и, следовательно, квантованных уровней энергии было значительным шагом к пониманию электронов в атомах, а также значительным шагом к развитию теории квантовая механика в предположении, что квантованные ограничения должны учитывать все прерывистые уровни энергии и спектры в атомах.
С де Бройль предположение о существовании электронных волн материи в 1924 г., и за короткое время до 1926 г. Уравнение Шредингера лечение водородоподобные атомы, можно было видеть, что "длина волны" боровского электрона является функцией его импульса, и, таким образом, было видно, что орбитальный электрон Бора вращается по кругу, кратному его половине длины волны.[а] В течение короткого времени модель Бора можно было рассматривать как классическую модель с дополнительным ограничением, обусловленным аргументом «длины волны». Однако этот период был немедленно заменен полной трехмерной волновой механикой 1926 года. В нашем нынешнем понимании физики модель Бора называется полуклассической моделью из-за ее квантования углового момента, а не из-за ее связи с длина волны электронов, которая появилась задним числом через десяток лет после того, как была предложена модель Бора.
Модель Бора смогла объяснить спектры излучения и поглощения водород. Энергии электронов в п = 1, 2, 3 и т.д. состояния в модели Бора соответствуют таковым в современной физике. Однако это не объясняет сходства между разными атомами, как это выражено в периодической таблице, например тот факт, что гелий (два электрона), неон (10 электронов) и аргон (18 электронов) проявляют аналогичную химическую инертность. Современное квантовая механика объясняет это с точки зрения электронные оболочки и подоболочки, каждая из которых может удерживать количество электронов, определяемое Принцип исключения Паули. Таким образом п = 1 может содержать один или два электрона, в то время как п = 2 состояние может содержать до восьми электронов в подоболочках 2s и 2p. В гелии все п = 1 состояние полностью занято; то же самое верно для п = 1 и п = 2 в неоне. В аргоне подоболочки 3s и 3p аналогичным образом полностью заняты восемью электронами; квантовая механика также допускает трехмерную подоболочку, но она имеет более высокую энергию, чем 3s и 3p в аргоне (в отличие от ситуации с атомом водорода), и остается пустой.
Современные концепции и связи с принципом неопределенности Гейзенберга
Незамедлительно после Гейзенберг обнаружил его принцип неопределенности,[17] Бор отметил, что существование каких-либо волновой пакет подразумевает неопределенность в частоте и длине волны, поскольку для создания самого пакета необходим разброс частот.[18] В квантовой механике, где все импульсы частиц связаны с волнами, именно формирование такого волнового пакета локализует волну и, следовательно, частицу в пространстве. В состояниях, в которых квантово-механическая частица связана, она должна быть локализована как волновой пакет, а существование пакета и его минимальный размер подразумевает разброс и минимальное значение длины волны частицы, а, следовательно, также импульса и энергии. В квантовой механике, когда частица локализуется в меньшей области пространства, связанный сжатый волновой пакет требует все большего и большего диапазона импульсов и, следовательно, большей кинетической энергии. Таким образом, энергия связи для удержания или захвата частицы в меньшей области пространства неограниченно увеличивается по мере того, как область пространства становится меньше. Частицы не могут быть ограничены геометрической точкой в пространстве, так как для этого потребуется бесконечный импульс частицы.
В химии, Шредингер, Полинг, Mulliken и другие отметили, что следствием соотношения Гейзенберга было то, что электрон как волновой пакет не мог считаться имеющим точное местоположение на своей орбитали. Макс Борн предположил, что положение электрона необходимо описывать распределение вероятностей что было связано с обнаружением электрона в некоторой точке волновой функции, которая описывала связанный с ним волновой пакет. Новая квантовая механика не дала точных результатов, а только вероятности появления множества возможных таких результатов. Гейзенберг считал, что путь движущейся частицы не имеет значения, если мы не можем его наблюдать, как мы не можем наблюдать электроны в атоме.
В квантовой картине Гейзенберга, Шредингера и других число атома Борап для каждой орбиты стала известна как n-сфера[нужна цитата ] в трехмерном атоме и изображалась как наиболее вероятная энергия облака вероятности электронного волнового пакета, окружающего атом.
Орбитальные имена
Орбитальная запись
Орбиталям даны имена, которые обычно даются в форме:
куда Икс уровень энергии, соответствующий главное квантовое число п; тип строчная буква, обозначающая форму, или подоболочка орбитали, соответствующей угловое квантовое число ℓ; и у это количество электронов на этой орбитали.
Например, орбитальная 1с2 (произносится как отдельные цифры и буквы: «'one' 'ess' 'two'») имеет два электрона и является самым низким уровнем энергии (п = 1) и имеет угловое квантовое число ℓ = 0, обозначается s.
Рентгеновское обозначение
Существует также другая, менее распространенная система, которая до сих пор используется в рентгенологии, известная как Рентгеновское обозначение, который является продолжением обозначений, использовавшихся до того, как орбитальная теория получила хорошее понимание. В этой системе главному квантовому числу присваивается связанная с ним буква. За п = 1, 2, 3, 4, 5, …, буквы, связанные с этими числами, - это K, L, M, N, O, ... соответственно.
Водородоподобные орбитали
Простейшие атомные орбитали - это те, которые рассчитываются для систем с одним электроном, таких как атом водорода. Атом любого другого элемента ионизированный вплоть до одного электрона очень похож на водород, и орбитали принимают такую же форму. В уравнении Шредингера для этой системы, состоящей из одной отрицательной и одной положительной частицы, атомные орбитали являются собственные состояния из Гамильтонов оператор для энергии. Их можно получить аналитически, а это означает, что полученные орбитали являются произведениями ряда полиномов, экспоненциальных и тригонометрических функций. (видеть атом водорода ).
Для атомов с двумя и более электронами основные уравнения могут быть решены только с использованием методов итерационной аппроксимации. Орбитали многоэлектронных атомов равны качественно похожи на водородные, и в простейших моделях принято иметь такую же форму. Для более строгого и точного анализа необходимо использовать численные приближения.
Данная (водородоподобная) атомная орбиталь идентифицируется уникальными значениями трех квантовых чисел: п, ℓ, и мℓ. Правила, ограничивающие значения квантовых чисел и их энергии (см. Ниже), объясняют электронную конфигурацию атомов и периодическая таблица.
Стационарные состояния (квантовые состояния ) водородоподобных атомов являются его атомными орбиталями.[требуется разъяснение ] Однако в целом поведение электрона не полностью описывается одной орбиталью. Электронные состояния лучше всего представлены зависящими от времени «смесями» (линейные комбинации ) кратных орбиталей. Видеть Линейная комбинация атомных орбиталей, метод молекулярных орбиталей.
Квантовое число п впервые появился в Модель Бора где он определяет радиус каждой круговой электронной орбиты. Однако в современной квантовой механике п определяет среднее расстояние электрона от ядра; все электроны с одинаковым значением п лежат на одинаковом среднем расстоянии. По этой причине орбитали с одинаковым значением п говорят, что содержат "ракушка ". Орбитали с одинаковым значением п а также такое же значениеℓ еще более тесно связаны и, как говорят, содержат "подоболочка ".
Квантовые числа
Из-за квантово-механической природы электронов вокруг ядра атомные орбитали могут быть однозначно определены набором целых чисел, известных как квантовые числа. Эти квантовые числа встречаются только в определенных комбинациях значений, и их физическая интерпретация меняется в зависимости от того, используются ли реальные или сложные версии атомных орбиталей.
Сложные орбитали
В физике наиболее распространенные орбитальные описания основаны на решениях для атома водорода, где орбитали задаются произведением радиальной функции и чистой сферической гармоники. Квантовые числа вместе с правилами, определяющими их возможные значения, следующие:
В главное квантовое число п описывает энергию электрона и всегда является положительное число. Фактически, это может быть любое положительное целое число, но по причинам, обсуждаемым ниже, большие числа встречаются редко. Каждый атом, как правило, имеет множество орбиталей, связанных с каждым значением п; эти орбитали вместе иногда называют электронные оболочки.
В азимутальное квантовое число ℓ описывает орбитальный угловой момент каждого электрона и является целым неотрицательным числом. Внутри оболочки, где п какое-то целое число п0, ℓ диапазоны всех (целых) значений, удовлетворяющих соотношению . Например, п = 1 оболочка имеет только орбитали с , а п = 2 оболочка имеет только орбитали с , и . Набор орбиталей, связанных с определенным значениемℓ иногда собирательно называют подоболочка.
В магнитное квантовое число, , описывает магнитный момент электрона в произвольном направлении и также всегда является целым числом. В подоболочке, где какое-то целое число , диапазоны таким образом: .
Вышеуказанные результаты можно обобщить в следующей таблице. Каждая ячейка представляет подоболочку и перечисляет значения доступный в этой подоболочке. Пустые ячейки представляют собой несуществующие подоболочки.
| ℓ = 0 | ℓ = 1 | ℓ = 2 | ℓ = 3 | ℓ = 4 | ... | |
|---|---|---|---|---|---|---|
| п = 1 | ||||||
| п = 2 | 0 | −1, 0, 1 | ||||
| п = 3 | 0 | −1, 0, 1 | −2, −1, 0, 1, 2 | |||
| п = 4 | 0 | −1, 0, 1 | −2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | ||
| п = 5 | 0 | −1, 0, 1 | −2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | |
| ... | ... | ... | ... | ... | ... | ... |
Подоболочки обычно идентифицируются по их - и -значения. представлен его числовым значением, но обозначается следующей буквой: 0 - буквой s, 1 - p, 2 - d, 3 - f, 4 - g. Например, можно говорить о подоболочке с и как «подоболочку 2s».
Каждый электрон также имеет квантовое число спина, s, который описывает спин каждого электрона (спин вверх или вниз). Номер s может быть +1/2 или -1/2.
В Принцип исключения Паули утверждает, что никакие два электрона в атоме не могут иметь одинаковые значения всех четырех квантовых чисел. Если есть два электрона на орбитали с заданными значениями для трех квантовых чисел, (п, ℓ, м) эти два электрона должны различаться своим спином.
Вышеупомянутые соглашения подразумевают предпочтительную ось (например, z направление в декартовых координатах), и они также подразумевают предпочтительное направление вдоль этой предпочтительной оси. Иначе не было бы смысла различать м = +1 из м = −1. Таким образом, модель наиболее полезна при применении к физическим системам, которые разделяют эти симметрии. В Эксперимент Штерна-Герлаха - когда атом подвергается воздействию магнитного поля - является одним из таких примеров.[19]
Реальные орбитали
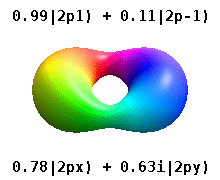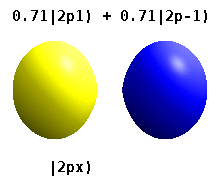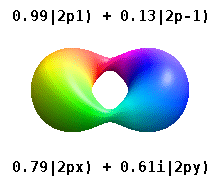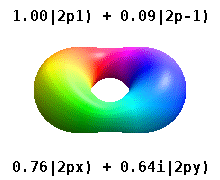
Атом, заключенный в кристаллическое твердое тело, ощущает несколько предпочтительных осей, но часто не имеет предпочтительного направления. Вместо того, чтобы строить атомные орбитали из произведения радиальных функций и одного сферическая гармоника обычно используются линейные комбинации сферических гармоник, разработанные таким образом, что мнимая часть сферических гармоник компенсируется. Эти реальные орбитали являются строительными блоками, которые чаще всего отображаются в орбитальных визуализациях.
На реальных водородоподобных орбиталях, например, п и ℓ имеют то же толкование и значение, что и их сложные аналоги, но м больше не является хорошим квантовым числом (хотя его абсолютное значение есть). Орбиталям даны новые имена в зависимости от их формы по отношению к стандартизированной декартовой основе. Реальные водородоподобные p-орбитали даются следующими[20][21]
куда п0 = рп 1 Y1 0, п1 = рп 1 Y1 1, и п−1 = рп 1 Y1 −1, - комплексные орбитали, соответствующие ℓ = 1.
Уравнения для pИкс и ру орбитали зависят от фазового соглашения, используемого для сферических гармоник. Приведенные выше уравнения предполагают, что сферические гармоники определяются формулой . Однако некоторые квантовые физики[22][23] включить фазовый фактор (−1)м в этих определениях, что означает связь между pИкс орбитально к разница сферических гармоник и pу орбитали к соответствующему сумма. (Подробнее см. Сферические гармоники # Условные обозначения ).
Формы орбиталей

Простые изображения, показывающие орбитальные формы, предназначены для описания угловых форм областей в космосе, где, вероятно, будут обнаружены электроны, занимающие орбиталь. Диаграммы не могут показать всю область, где можно найти электрон, поскольку согласно квантовой механике существует ненулевая вероятность найти электрон (почти) в любом месте пространства. Вместо этого диаграммы являются приблизительным изображением границы или контурные поверхности где плотность вероятности | ψ (р, θ, φ) |2 имеет постоянное значение, выбранное так, чтобы была определенная вероятность (например, 90%) нахождения электрона внутри контура. Несмотря на то что | ψ |2 как квадрат абсолютная величина везде неотрицательно, знак волновая функция ψ (р, θ, φ) часто указывается в каждой подобласти орбитального изображения.
Иногда ψ функция будет отображена на графике, чтобы показать ее фазы, а не | ψ (р, θ, φ) |2 который показывает плотность вероятности, но не имеет фаз (которые были потеряны в процессе получения абсолютного значения, поскольку ψ (р, θ, φ) - комплексное число). | ψ (р, θ, φ) |2 орбитальные графы, как правило, имеют менее сферические и более тонкие лепестки, чем ψ (р, θ, φ) графы, но имеют одинаковое количество лепестков в одних и тех же местах и в остальном узнаваемы. В этой статье, чтобы показать фазы волновой функции, в основном ψ (р, θ, φ) графики.
Доли можно рассматривать как стоячая волна вмешательство узоры между двумя встречно вращающимися, кольцевыми резонансными бегущая волна "м" и "−м«моды, с проекцией орбитали на плоскость xy, имеющую резонансный»м"длины волн по окружности. Хотя решения бегущей волны изображаются редко, их можно рассматривать как вращающиеся полосчатые торы с полосами, представляющими фазовую информацию. Для каждого м есть два решения стоячей волны ⟨м⟩+⟨−м⟩ и ⟨м⟩−⟨−м⟩. Для случая, когда м = 0 орбиталь вертикальная, информация о встречном вращении неизвестна, а орбиталь z-ось симметричная. Для случая, когда ℓ = 0 нет режимов встречного вращения. Есть только радиальные моды, а форма сферически симметрична. Для любого данного п, чем меньше ℓ тем больше радиальных узлов. Для любого данного ℓ, чем меньше п есть меньшее количество радиальных узлов (ноль для п сначала это ℓ орбитальный). Грубо говоря п это энергия, ℓ аналогично эксцентриситет, и м ориентация. В классическом случае кольцевая резонансная бегущая волна, например, в кольцевой линии передачи, если ее активно не форсировать, спонтанно распадается на кольцевую резонансную стоячую волну, поскольку отражения со временем будут нарастать даже при малейшем дефекте или неоднородности.
Вообще говоря, число п определяет размер и энергию орбитали для данного ядра: как п увеличивается, размер орбитали увеличивается. При сравнении разных элементов больший заряд ядра Z более тяжелых элементов заставляет их орбитали сжиматься по сравнению с более легкими, так что общий размер всего атома остается примерно постоянным, даже если количество электронов в более тяжелых элементах (большее Z) увеличивается.

Также в общих чертах, ℓ определяет форму орбиты, и мℓ его ориентация. Однако, поскольку некоторые орбитали описываются уравнениями в сложные числа форма иногда зависит от мℓ также. Вместе весь набор орбиталей для данного ℓ и п заполняйте пространство как можно более симметрично, но со все более сложными наборами лепестков и узлов.
Одиночные s-орбитали () имеют форму сфер. За п = 1 это примерно твердый шар (он наиболее плотный в центре и экспоненциально затухает снаружи), но для п = 2 или более, каждая одиночная s-орбиталь состоит из сферически симметричных поверхностей, которые представляют собой вложенные оболочки (т.е. «волновая структура» является радиальной, а также следует за синусоидальной радиальной составляющей). См. Изображение поперечного сечения этих вложенных оболочек справа. S-орбитали для всех п числа - единственные орбитали с антиузлом (областью высокой плотности волновой функции) в центре ядра. Все остальные орбитали (p, d, f и т. Д.) Имеют угловой момент и, таким образом, избегают ядра (имеющего волновой узел в ядро). Недавно была предпринята попытка экспериментального изображения 1s и 2p орбиталей в SrTiO3 кристалл с помощью сканирующей просвечивающей электронной микроскопии с энергодисперсионной рентгеновской спектроскопией.[24] Поскольку визуализация проводилась с использованием электронного луча, кулоновское лучево-орбитальное взаимодействие, которое часто называют эффектом прицельного параметра, включается в окончательный результат (см. Рисунок справа).
Формы p, d и f-орбиталей описаны здесь словесно и графически показаны в Таблица орбиталей ниже. Три p-орбитали для п = 2 имеют форму двух эллипсоиды с точка касания на ядро (двухлепестковая форма иногда упоминается как "гантель "- есть две доли, направленные в противоположные стороны друг от друга). Три p-орбитали в каждой ракушка ориентированы под прямым углом друг к другу, что определяется их соответствующей линейной комбинацией значениймℓ. Общий результат - лепесток, указывающий вдоль каждого направления основных осей.
Четыре из пяти d-орбиталей для п = 3 выглядят одинаково, каждая с четырьмя грушевидными лепестками, каждая из которых касается двух других под прямым углом, а центры всех четырех лежат в одной плоскости. Три из этих плоскостей являются плоскостями xy, xz и yz - лепестки находятся между парами первичных осей, а четвертая имеет центры вдоль самих осей x и y. Пятая и последняя d-орбиталь состоит из трех областей с высокой плотностью вероятности: тор с двумя грушевидными областями, расположенными симметрично относительно оси z. Всего 18 направленных лепестков указывают в каждом направлении первичной оси и между каждой парой.
Существует семь f-орбиталей, каждая из которых имеет более сложную форму, чем d-орбитали.
Кроме того, как и в случае с s-орбиталями, отдельные p, d, f и g орбитали с п значения выше, чем наименьшее возможное значение, демонстрируют дополнительную радиальную узловую структуру, которая напоминает гармонические волны того же типа по сравнению с самой низкой (или основной) модой волны. Как и в случае с s-орбиталями, это явление обеспечивает орбитали p, d, f и g на следующем более высоком возможном значении п (например, 3p-орбитали против основного 2p), дополнительный узел в каждой доле. Еще более высокие значения п дополнительно увеличивайте количество радиальных узлов для каждого типа орбиталей.
Формы атомных орбиталей в одноэлектронном атоме связаны с трехмерным сферические гармоники. Эти формы не уникальны, и допустима любая линейная комбинация, например преобразование в кубические гармоники, на самом деле можно сгенерировать наборы, в которых все d имеют одинаковую форму, как и пИкс, пу, и пz одинаковой формы.[25][26]
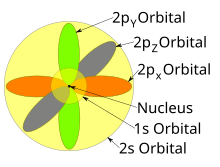
Хотя отдельные орбитали чаще всего показаны независимыми друг от друга, орбитали сосуществуют вокруг ядра в одно и то же время. Также в 1927 г. Альбрехт Унсельд proved that if one sums the electron density of all orbitals of a particular azimuthal quantum number ℓ of the same shell п (e.g. all three 2p orbitals, or all five 3d orbitals) where each orbital is occupied by an electron or each is occupied by an electron pair, then all angular dependence disappears; that is, the resulting total density of all the atomic orbitals in that subshell (those with the same ℓ) is spherical. Это известно как Unsöld's theorem.
Orbitals table
This table shows all orbital configurations for the real hydrogen-like wave functions up to 7s, and therefore covers the simple electronic configuration for all elements in the periodic table up to радий. "ψ" graphs are shown with − и + волновая функция phases shown in two different colors (arbitrarily red and blue). В пz orbital is the same as the п0 orbital, but the пИкс и пу are formed by taking linearcombinations of the п+1 и п−1 orbitals (which is why they are listed under the м = ±1 метка). Так же п+1 и п−1 are notthe same shape as the п0, since they are pure сферические гармоники.
| s (ℓ = 0) | p (ℓ = 1) | d (ℓ = 2) | f (ℓ = 3) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| м = 0 | м = 0 | м = ±1 | м = 0 | м = ±1 | м = ±2 | м = 0 | м = ±1 | м = ±2 | м = ±3 | |||||||
| s | пz | пИкс | пу | dz2 | dxz | dyz | dху | dИкс2−y2 | жz3 | жxz2 | жyz2 | жxyz | жz(x2−y2) | жx(x2−3y2) | жy(3x2−y2) | |
| п = 1 |  | |||||||||||||||
| п = 2 |  |  |  |  | ||||||||||||
| п = 3 |  |  |  |  |  |  |  |  |  | |||||||
| п = 4 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
| п = 5 |  |  |  |  |  |  |  |  |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| п = 6 |  |  |  |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| п = 7 |  | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
Qualitative understanding of shapes
The shapes of atomic orbitals can be qualitatively understood by considering the analogous case of standing waves on a circular drum.[27] To see the analogy, the mean vibrational displacement of each bit of drum membrane from the equilibrium point over many cycles (a measure of average drum membrane velocity and momentum at that point) must be considered relative to that point's distance from the center of the drum head. If this displacement is taken as being analogous to the probability of finding an electron at a given distance from the nucleus, then it will be seen that the many modes of the vibrating disk form patterns that trace the various shapes of atomic orbitals. The basic reason for this correspondence lies in the fact that the distribution of kinetic energy and momentum in a matter-wave is predictive of where the particle associated with the wave will be. That is, the probability of finding an electron at a given place is also a function of the electron's average momentum at that point, since high electron momentum at a given position tends to "localize" the electron in that position, via the properties of electron wave-packets (see the Принцип неопределенности Гейзенберга for details of the mechanism).
This relationship means that certain key features can be observed in both drum membrane modes and atomic orbitals. For example, in all of the modes analogous to s orbitals (the top row in the animated illustration below), it can be seen that the very center of the drum membrane vibrates most strongly, corresponding to the antinode в целом s orbitals in an atom. This antinode means the electron is most likely to be at the physical position of the nucleus (which it passes straight through without scattering or striking it), since it is moving (on average) most rapidly at that point, giving it maximal momentum.
A mental "planetary orbit" picture closest to the behavior of electrons in s orbitals, all of which have no angular momentum, might perhaps be that of a Кеплеровская орбита с орбитальный эксцентриситет of 1 but a finite major axis, not physically possible (because частицы were to collide), but can be imagined as a предел of orbits with equal major axes but increasing eccentricity.
Below, a number of drum membrane vibration modes and the respective wave functions of the hydrogen atom are shown. A correspondence can be considered where the wave functions of a vibrating drum head are for a two-coordinate system ψ (р, θ) and the wave functions for a vibrating sphere are three-coordinate ψ (р, θ, φ).
- s-type drum modes and wave functions

Drum mode

Drum mode

Drum mode

Wave function of 1s orbital (real part, 2D-cut, )

Wave function of 2s orbital (real part, 2D-cut, )

Wave function of 3s orbital (real part, 2D-cut, )
None of the other sets of modes in a drum membrane have a central antinode, and in all of them the center of the drum does not move. These correspond to a node at the nucleus for all non-s orbitals in an atom. These orbitals all have some angular momentum, and in the planetary model, they correspond to particles in orbit with eccentricity less than 1.0, so that they do not pass straight through the center of the primary body, but keep somewhat away from it.
In addition, the drum modes analogous to п и d modes in an atom show spatial irregularity along the different radial directions from the center of the drum, whereas all of the modes analogous to s modes are perfectly symmetrical in radial direction. The non radial-symmetry properties of non-s orbitals are necessary to localize a particle with angular momentum and a wave nature in an orbital where it must tend to stay away from the central attraction force, since any particle localized at the point of central attraction could have no angular momentum. For these modes, waves in the drum head tend to avoid the central point. Such features again emphasize that the shapes of atomic orbitals are a direct consequence of the wave nature of electrons.
- p-type drum modes and wave functions

Drum mode

Drum mode

Drum mode

Wave function of 2p orbital (real part, 2D-cut, )
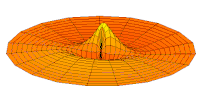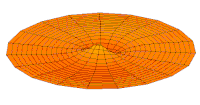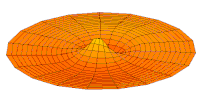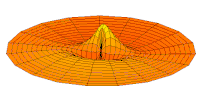
Wave function of 3p orbital (real part, 2D-cut, )

Wave function of 4p orbital (real part, 2D-cut, )
- d-type drum modes

Режим (3d orbital)

Режим (4d orbital)

Режим (5d orbital)
Орбитальная энергия
In atoms with a single electron (водородоподобные атомы ), the energy of an orbital (and, consequently, of any electrons in the orbital) is determined mainly by . В orbital has the lowest possible energy in the atom. Each successively higher value of has a higher level of energy, but the difference decreases as увеличивается. For high , the level of energy becomes so high that the electron can easily escape from the atom. In single electron atoms, all levels with different в пределах данного are degenerate in the Schrödinger approximation, and have the same energy. This approximation is broken to a slight extent in the solution to the Dirac equation (where the energy depends on п and another quantum number j), and by the effect of the magnetic field of the nucleus and квантовая электродинамика последствия. The latter induce tiny binding energy differences especially for s electrons that go nearer the nucleus, since these feel a very slightly different nuclear charge, even in one-electron atoms; видеть Баранина сдвиг.
In atoms with multiple electrons, the energy of an electron depends not only on the intrinsic properties of its orbital, but also on its interactions with the other electrons. These interactions depend on the detail of its spatial probability distribution, and so the уровни энергии of orbitals depend not only on but also on . Higher values of are associated with higher values of energy; for instance, the 2p state is higher than the 2s state. Когда , the increase in energy of the orbital becomes so large as to push the energy of orbital above the energy of the s-orbital in the next higher shell; когда the energy is pushed into the shell two steps higher. The filling of the 3d orbitals does not occur until the 4s orbitals have been filled.
The increase in energy for subshells of increasing angular momentum in larger atoms is due to electron–electron interaction effects, and it is specifically related to the ability of low angular momentum electrons to penetrate more effectively toward the nucleus, where they are subject to less screening from the charge of intervening electrons. Thus, in atoms of higher atomic number, the of electrons becomes more and more of a determining factor in their energy, and the principal quantum numbers of electrons becomes less and less important in their energy placement.
The energy sequence of the first 35 subshells (e.g., 1s, 2p, 3d, etc.) is given in the following table. Each cell represents a subshell with и given by its row and column indices, respectively. The number in the cell is the subshell's position in the sequence. For a linear listing of the subshells in terms of increasing energies in multielectron atoms, see the section below.
| s | п | d | ж | грамм | час | |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 2 | 3 | ||||
| 3 | 4 | 5 | 7 | |||
| 4 | 6 | 8 | 10 | 13 | ||
| 5 | 9 | 11 | 14 | 17 | 21 | |
| 6 | 12 | 15 | 18 | 22 | 26 | 31 |
| 7 | 16 | 19 | 23 | 27 | 32 | 37 |
| 8 | 20 | 24 | 28 | 33 | 38 | 44 |
| 9 | 25 | 29 | 34 | 39 | 45 | 51 |
| 10 | 30 | 35 | 40 | 46 | 52 | 59 |
Note: empty cells indicate non-existent sublevels, while numbers in italics indicate sublevels that could (potentially) exist, but which do not hold electrons in any element currently known.
Electron placement and the periodic table

Several rules govern the placement of electrons in orbitals (электронная конфигурация ). The first dictates that no two electrons in an atom may have the same set of values of quantum numbers (this is the Принцип исключения Паули ). These quantum numbers include the three that define orbitals, as well as s, или же spin quantum number. Thus, two electrons may occupy a single orbital, so long as they have different values ofs. Тем не мение, Только two electrons, because of their spin, can be associated with each orbital.
Additionally, an electron always tends to fall to the lowest possible energy state. It is possible for it to occupy any orbital so long as it does not violate the Pauli exclusion principle, but if lower-energy orbitals are available, this condition is unstable. The electron will eventually lose energy (by releasing a фотон ) and drop into the lower orbital. Thus, electrons fill orbitals in the order specified by the energy sequence given above.
This behavior is responsible for the structure of the периодическая таблица. The table may be divided into several rows (called 'periods'), numbered starting with 1 at the top. The presently known elements occupy seven periods. If a certain period has number я, it consists of elements whose outermost electrons fall in the яth shell. Нильс Бор was the first to propose (1923) that the периодичность in the properties of the elements might be explained by the periodic filling of the electron energy levels, resulting in the electronic structure of the atom.[28]
The periodic table may also be divided into several numbered rectangular 'блоки '. The elements belonging to a given block have this common feature: their highest-energy electrons all belong to the same ℓ-state (but the п associated with that ℓ-state depends upon the period). For instance, the leftmost two columns constitute the 's-block'. The outermost electrons of Ли и Быть respectively belong to the 2s subshell, and those of Na и Mg to the 3s subshell.
The following is the order for filling the "subshell" orbitals, which also gives the order of the "blocks" in the periodic table:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p
The "periodic" nature of the filling of orbitals, as well as emergence of the s, п, d, и ж "blocks", is more obvious if this order of filling is given in matrix form, with increasing principal quantum numbers starting the new rows ("periods") in the matrix. Then, each subshell (composed of the first two quantum numbers) is repeated as many times as required for each pair of electrons it may contain. The result is a compressed periodic table, with each entry representing two successive elements:
| 1 с | |||||||||||||||
| 2 с | 2p | 2p | 2p | ||||||||||||
| 3 с | 3p | 3p | 3p | ||||||||||||
| 4 с | 3D | 3D | 3D | 3D | 3D | 4p | 4p | 4p | |||||||
| 5 с | 4d | 4d | 4d | 4d | 4d | 5p | 5p | 5p | |||||||
| 6 с | 4f | 4f | 4f | 4f | 4f | 4f | 4f | 5d | 5d | 5d | 5d | 5d | 6p | 6p | 6p |
| 7 с | 5f | 5f | 5f | 5f | 5f | 5f | 5f | 6d | 6d | 6d | 6d | 6d | 7p | 7p | 7p |
Although this is the general order of orbital filling according to the Madelung rule, there are exceptions, and the actual electronic energies of each element are also dependent upon additional details of the atoms (see Electron configuration#Atoms: Aufbau principle and Madelung rule ).
The number of electrons in an electrically neutral atom increases with the атомный номер. The electrons in the outermost shell, or валентные электроны, tend to be responsible for an element's chemical behavior. Elements that contain the same number of valence electrons can be grouped together and display similar chemical properties.
Релятивистские эффекты
For elements with high atomic number Z, the effects of relativity become more pronounced, and especially so for s electrons, which move at relativistic velocities as they penetrate the screening electrons near the core of high-Z атомы. This relativistic increase in momentum for high speed electrons causes a corresponding decrease in wavelength and contraction of 6s orbitals relative to 5d orbitals (by comparison to corresponding s and d electrons in lighter elements in the same column of the periodic table); this results in 6s valence electrons becoming lowered in energy.
Examples of significant physical outcomes of this effect include the lowered melting temperature of Меркурий (which results from 6s electrons not being available for metal bonding) and the golden color of золото и цезий.[29]
в Модель Бора, п = 1 electron has a velocity given by , куда Z is the atomic number, это постоянная тонкой структуры, и c это скорость света. In non-relativistic quantum mechanics, therefore, any atom with an atomic number greater than 137 would require its 1s electrons to be traveling faster than the speed of light. Даже в Уравнение Дирака, which accounts for relativistic effects, the wave function of the electron for atoms with is oscillatory and unbounded. The significance of element 137, also known as untriseptium, was first pointed out by the physicist Ричард Фейнман. Element 137 is sometimes informally called feynmanium (symbol Fy).[30] However, Feynman's approximation fails to predict the exact critical value of Z due to the non-point-charge nature of the nucleus and very small orbital radius of inner electrons, resulting in a potential seen by inner electrons which is effectively less than Z. Критический Z value, which makes the atom unstable with regard to high-field breakdown of the vacuum and production of electron-positron pairs, does not occur until Z is about 173. These conditions are not seen except transiently in collisions of very heavy nuclei such as lead or uranium in accelerators, where such electron-positron production from these effects has been claimed to be observed.
There are no nodes in relativistic orbital densities, although individual components of the wave function will have nodes.[31]
pp hybridisation (conjectured)
В конце period-8 elements a hybrid of 8p3/2 and 9p1/2 is expected to exist,[32] where "3/2" and "1/2" refer to the total angular momentum quantum number. This "pp" hybrid may be responsible for the p-блок of the period due to properties similar to p subshells in ordinary валентные оболочки. Energy levels of 8p3/2 and 9p1/2 come close due to relativistic spin–orbit effects; the 9s subshell should also participate, as these elements are expected to be analogous to the respective 5p elements индий через ксенон.
Transitions between orbitals
Bound quantum states have discrete energy levels. When applied to atomic orbitals, this means that the energy differences between states are also discrete. A transition between these states (i.e., an electron absorbing or emitting a photon) can thus only happen if the photon has an energy corresponding with the exact energy difference between said states.
Consider two states of the hydrogen atom:
State 1) п = 1, ℓ = 0, мℓ = 0 и s = +1/2
State 2) п = 2, ℓ = 0, мℓ = 0 и s = +1/2
By quantum theory, state 1 has a fixed energy of E1, and state 2 has a fixed energy of E2. Now, what would happen if an electron in state 1 were to move to state 2? For this to happen, the electron would need to gain an energy of exactly E2 − E1. If the electron receives energy that is less than or greater than this value, it cannot jump from state 1 to state 2. Now, suppose we irradiate the atom with a broad-spectrum of light. Photons that reach the atom that have an energy of exactly E2 − E1 will be absorbed by the electron in state 1, and that electron will jump to state 2. However, photons that are greater or lower in energy cannot be absorbed by the electron, because the electron can only jump to one of the orbitals, it cannot jump to a state between orbitals. The result is that only photons of a specific frequency will be absorbed by the atom. This creates a line in the spectrum, known as an absorption line, which corresponds to the energy difference between states 1 and 2.
The atomic orbital model thus predicts line spectra, which are observed experimentally. This is one of the main validations of the atomic orbital model.
The atomic orbital model is nevertheless an approximation to the full quantum theory, which only recognizes many electron states. The predictions of line spectra are qualitatively useful but are not quantitatively accurate for atoms and ions other than those containing only one electron.
Смотрите также
Рекомендации
Сноски
- ^ This physically incorrect Bohr model is still often taught to beginning students.[нужна цитата ]
Цитаты
- ^ Orchin, Milton; Macomber, Roger S.; Pinhas, Allan; Wilson, R. Marshall (2005). Atomic Orbital Theory (PDF).
- ^ Daintith, J. (2004). Oxford Dictionary of Chemistry. Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-860918-6.
- ^ Griffiths, David (1995). Введение в квантовую механику. Прентис Холл. С. 190–191. ISBN 978-0-13-124405-4.
- ^ Levine, Ira (2000). Квантовая химия (5-е изд.). Прентис Холл. стр.144–145. ISBN 978-0-13-685512-5.
- ^ Laidler, Keith J.; Meiser, John H. (1982). Физическая химия. Бенджамин / Каммингс. п. 488. ISBN 978-0-8053-5682-3.
- ^ Аткинс, Питер; de Paula, Julio; Friedman, Ronald (2009). Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry. Издательство Оксфордского университета. п. 106. ISBN 978-0-19-920606-3.
- ^ Feynman, Richard; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics -The Definitive Edition, Vol 1 lect 6. Pearson PLC, Addison Wesley. п. 11. ISBN 978-0-8053-9046-9.
- ^ Роджер Пенроуз, Дорога к реальности
- ^ Mulliken, Robert S. (July 1932). "Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations". Физический обзор. 41 (1): 49–71. Bibcode:1932PhRv...41...49M. Дои:10.1103/PhysRev.41.49.
- ^ а б Bohr, Niels (1913). "On the Constitution of Atoms and Molecules". Философский журнал. 26 (1): 476. Bibcode:1914Natur..93..268N. Дои:10.1038/093268a0. S2CID 3977652.
- ^ а б Nagaoka, Hantaro (May 1904). «Кинетика системы частиц, иллюстрирующая линейный и полосовой спектр и явления радиоактивности». Философский журнал. 7 (41): 445–455. Дои:10.1080/14786440409463141. Архивировано из оригинал on 2017-11-27. Получено 2009-05-30.
- ^ Bryson, Bill (2003). Краткая история почти всего. Бродвейские книги. стр.141 –143. ISBN 978-0-7679-0818-4.
- ^ Thomson, J. J. (1897). "Cathode rays". Философский журнал. 44 (269): 293. Дои:10.1080/14786449708621070.
- ^ Thomson, J. J. (1904). "О строении атома: исследование устойчивости и периодов колебаний ряда корпускул, расположенных через равные промежутки времени по окружности круга; с применением результатов к теории строения атома" (выписка из статьи). Философский журнал. 6 серия. 7 (39): 237–265. Дои:10.1080/14786440409463107.
- ^ Родос, Ричард (1995). Создание атомной бомбы. Саймон и Шустер. С. 50–51. ISBN 978-0-684-81378-3.
- ^ Nagaoka, Hantaro (May 1904). «Кинетика системы частиц, иллюстрирующая линейный и полосовой спектр и явления радиоактивности». Философский журнал. 7 (41): 446. Дои:10.1080/14786440409463141. Архивировано из оригинал on 2017-11-27. Получено 2009-05-30.
- ^ Heisenberg, W. (March 1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Zeitschrift für Physik A. 43 (3–4): 172–198. Bibcode:1927ZPhy...43..172H. Дои:10.1007/BF01397280. S2CID 122763326.
- ^ Bohr, Niels (April 1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Природа. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. Дои:10.1038/121580a0.
- ^ Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik. 9 (1): 353–355. Bibcode:1922ZPhy....9..353G. Дои:10.1007/BF01326984. S2CID 126109346.
- ^ Levine, Ira (2014). Квантовая химия (7-е изд.). Pearson Education. С. 141–2. ISBN 978-0-321-80345-0.
- ^ Blanco, Miguel A.; Flórez, M.; Bermejo, M. (December 1997). "Evaluation of the rotation matrices in the basis of real spherical harmonics". Журнал молекулярной структуры: ТЕОХИМА. 419 (1–3): 19–27. Дои:10.1016/S0166-1280(97)00185-1.
- ^ Messiah, Albert (1999). Quantum mechanics : two volumes bound as one (Two vol. bound as one, unabridged reprint ed.). Минеола, Нью-Йорк: Дувр. ISBN 978-0-486-40924-5.
- ^ Claude Cohen-Tannoudji; Бернар Диу; Franck Laloë; и другие. (1996). Квантовая механика. Translated by from the French by Susan Reid Hemley. Wiley-Interscience. ISBN 978-0-471-56952-7.
- ^ а б Jeong, Jong Seok; Odlyzko, Michael L.; Xu, Peng; Jalan, Bharat; Mkhoyan, K. Andre (2016-04-26). "Probing core-electron orbitals by scanning transmission electron microscopy and measuring the delocalization of core-level excitations". Физический обзор B. 93 (16): 165140. Bibcode:2016PhRvB..93p5140J. Дои:10.1103/PhysRevB.93.165140.
- ^ Powell, Richard E. (1968). "The five equivalent d orbitals". Журнал химического образования. 45 (1): 45. Bibcode:1968JChEd..45...45P. Дои:10.1021/ed045p45.
- ^ Kimball, George E. (1940). "Directed Valence". Журнал химической физики. 8 (2): 188. Bibcode:1940JChPh...8..188K. Дои:10.1063/1.1750628.
- ^ Cazenave, Lions, T., P.; Lions, P. L. (1982). "Orbital stability of standing waves for some nonlinear Schrödinger equations". Коммуникации по математической физике. 85 (4): 549–561. Bibcode:1982CMaPh..85..549C. Дои:10.1007/BF01403504. S2CID 120472894.
- ^ Бор, Нильс (1923). "Über die Anwendung der Quantumtheorie auf den Atombau. I". Zeitschrift für Physik. 13 (1): 117. Bibcode:1923ZPhy...13..117B. Дои:10.1007/BF01328209.
- ^ Lower, Stephen. "Primer on Quantum Theory of the Atom".
- ^ Poliakoff, Martyn; Tang, Samantha (9 February 2015). "The periodic table: icon and inspiration". Философские труды Королевского общества A. 373 (2037): 20140211. Bibcode:2015RSPTA.37340211P. Дои:10.1098/rsta.2014.0211. PMID 25666072.
- ^ Szabo, Attila (1969). "Contour diagrams for relativistic orbitals". Журнал химического образования. 46 (10): 678. Bibcode:1969JChEd..46..678S. Дои:10.1021/ed046p678.
- ^ Fricke, Burkhard (1975). Superheavy elements: a prediction of their chemical and physical properties. Recent Impact of Physics on Inorganic Chemistry. Структура и связь. 21. стр.89–144. Дои:10.1007/BFb0116498. ISBN 978-3-540-07109-9. Получено 4 октября 2013.
- McCaw, Charles S. (2015). Orbitals: With Applications in Atomic Spectra. Сингапур: Всемирная научная издательская компания. ISBN 9781783264162.
- Tipler, Paul; Llewellyn, Ralph (2003). Modern Physics (4-е изд.). Нью-Йорк: В. Х. Фриман и компания. ISBN 978-0-7167-4345-3.
- Scerri, Eric (2007). The Periodic Table, Its Story and Its Significance. Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0-19-530573-9.
- Levine, Ira (2014). Квантовая химия (7-е изд.). Pearson Education. ISBN 978-0-321-80345-0.
- Griffiths, David (2000). Введение в квантовую механику (2-е изд.). Бенджамин Каммингс. ISBN 978-0-13-111892-8.
- Cohen, Irwin; Bustard, Thomas (1966). "Atomic Orbitals: Limitations and Variations". J. Chem. Образовательный. 43 (4): 187. Bibcode:1966JChEd..43..187C. Дои:10.1021/ed043p187.
внешняя ссылка
- Guide to atomic orbitals
- Covalent Bonds and Molecular Structure
- Animation of the time evolution of an hydrogenic orbital
- The Orbitron, a visualization of all common and uncommon atomic orbitals, from 1s to 7g
- Grand table Still images of many orbitals





















































