Преобразование Мёбиуса - Möbius transformation

В геометрия и комплексный анализ, а Преобразование Мёбиуса из комплексная плоскость это рациональная функция формы

${ displaystyle f (z) = { frac {az + b} {cz + d}}}$

одного сложный Переменная z; здесь коэффициенты а, б, c, d комплексные числа, удовлетворяющие объявление − до н.э ≠ 0.

Геометрически преобразование Мёбиуса может быть получено, если сначала выполнить стереографическая проекция из самолета в единичная двусфера, вращая и перемещая сферу в новое место и ориентируясь в пространстве, а затем выполняя стереографическую проекцию (из нового положения сферы) на плоскость.^[1]Эти преобразования сохраняют углы, отображают каждую прямую линию на линию или круг и отображают каждый круг на линию или круг.

Преобразования Мёбиуса - это проективные преобразования из сложная проективная линия. Они образуют группа называется Группа Мебиуса, какой проективная линейная группа PGL (2,C). Вместе со своим подгруппы, он имеет множество приложений в математике и физике.

Преобразования Мёбиуса названы в честь Август Фердинанд Мёбиус; они также имеют разные названия омографии, гомографические преобразования, дробно-линейные преобразования, билинейные преобразования, или же дробно-линейные преобразования.

Обзор

Преобразования Мёбиуса определены на расширенная комплексная плоскость ${ displaystyle { widehat { mathbf {C}}} = mathbf {C} cup { infty }}$ (т.е. комплексная плоскость дополненный точка в бесконечности ).

Стереографическая проекция определяет ${ displaystyle { widehat { mathbf {C}}}}$ сферой, которую тогда называют Сфера Римана; альтернативно, ${ displaystyle { widehat { mathbf {C}}}}$ можно рассматривать как сложный проективная линия ${ Displaystyle mathbf {C} mathbf {P} ^ {1}}$. Преобразования Мёбиуса - это в точности биективный конформный отображает из сферы Римана в себя, т.е. автоморфизмы сферы Римана как комплексное многообразие; в качестве альтернативы, они являются автоморфизмами ${ Displaystyle mathbf {C} mathbf {P} ^ {1}}$ как алгебраическое многообразие. Следовательно, множество всех преобразований Мёбиуса образует группа под сочинение. Эта группа называется группой Мёбиуса и иногда обозначается ${ displaystyle operatorname {Aut} ({ widehat { mathbf {C}}}) ,}$.

Группа Мёбиуса изоморфный в группу сохраняющих ориентацию изометрии из гиперболическое 3-пространство и поэтому играет важную роль при изучении гиперболические трехмерные многообразия.

В физика, то компонент идентичности из Группа Лоренца действует на небесная сфера так же, как группа Мёбиуса действует на сфере Римана. Фактически, эти две группы изоморфны. Наблюдатель, который ускоряется до релятивистских скоростей, увидит, как структура созвездий, наблюдаемая вблизи Земли, непрерывно трансформируется в соответствии с бесконечно малыми преобразованиями Мёбиуса. Это наблюдение часто принимается за отправную точку твисторная теория.

Определенный подгруппы группы Мёбиуса образуют группы автоморфизмов другого односвязный Римановы поверхности ( комплексная плоскость и гиперболическая плоскость ). Таким образом, преобразования Мёбиуса играют важную роль в теории Римановы поверхности. В фундаментальная группа любой римановой поверхности является дискретная подгруппа группы Мёбиуса (см. Фуксова группа и Клейнианская группа Особенно важной дискретной подгруппой группы Мёбиуса является модульная группа; это центральное место в теории многих фракталы, модульные формы, эллиптические кривые и Уравнения Пеллиана.

В более общем смысле преобразования Мёбиуса можно определить в пространствах размерности п> 2 как биективные конформные сохраняющие ориентацию отображения из п-сфера к п-сфера. Такое преобразование является наиболее общей формой конформного отображения области. В соответствии с Теорема Лиувилля преобразование Мёбиуса может быть выражено как композиция переводов, сходства, ортогональные преобразования и обращения.

Определение

Общий вид преобразования Мёбиуса дается формулой

${ displaystyle f (z) = { frac {az + b} {cz + d}}}$

куда а, б, c, d какие-нибудь сложные числа удовлетворение объявление − до н.э ≠ 0. Если объявление = до н.э, рациональная функция, определенная выше, является константой, поскольку

${ displaystyle f (z) = { frac {az + b} {cz + d}} = { frac {a (cz + d)} {c (cz + d)}} - { frac {ad- bc} {c (cz + d)}} = { frac {a} {c}}}$

и поэтому не считается преобразованием Мёбиуса.

В случае c ≠ 0, это определение распространяется на все Сфера Римана определяя

${ displaystyle f left ({ frac {-d} {c}} right) = infty { text {and}} f ( infty) = { frac {a} {c}}.}$

Если c = 0, мы определяем

${ Displaystyle е ( infty) = infty.}$

Таким образом, преобразование Мёбиуса всегда биективно. голоморфная функция от сферы Римана к сфере Римана.

Множество всех преобразований Мёбиуса образует группа под сочинение. Этой группе можно придать структуру комплексное многообразие таким образом, что композиция и инверсия голоморфные отображения. Тогда группа Мёбиуса является комплексная группа Ли. Группа Мёбиуса обычно обозначается ${ displaystyle operatorname {Aut} ({ widehat { mathbf {C}}})}$ как это группа автоморфизмов сферы Римана.

Фиксированные точки

Каждое неединичное преобразование Мёбиуса имеет два фиксированные точки ${ displaystyle gamma _ {1}, gamma _ {2}}$ на сфере Римана. Обратите внимание, что фиксированные точки здесь подсчитываются с множественность; параболические преобразования - это преобразования, в которых неподвижные точки совпадают. Одна или обе эти неподвижные точки могут быть бесконечно удаленными.

Определение фиксированных точек

Неподвижные точки преобразования

${ displaystyle f (z) = { frac {az + b} {cz + d}}}$

получаются решением уравнения неподвижной точки f (γ) = γ. За c 0, у этого есть два корня, полученные разложением этого уравнения на

${ Displaystyle с гамма ^ {2} - (а-г) гамма -b = 0 ,}$

и применяя квадратичная формула. Корни

${ displaystyle gamma _ {1,2} = { frac {(ad) pm { sqrt {(ad) ^ {2} + 4bc}}} {2c}} = { frac {(ad) pm { sqrt { Delta}}} {2c}}}$

с дискриминантом

${ displaystyle Delta = ( operatorname {tr} { mathfrak {H}}) ^ {2} -4 operatorname {det} { mathfrak {H}} = (a + d) ^ {2} -4 (ad-bc)}$.

Параболические преобразования имеют совпадающие неподвижные точки из-за нулевого дискриминанта. За c ненулевой и ненулевой дискриминант преобразование является эллиптическим или гиперболическим.

Когда c = 0 квадратное уравнение вырождается в линейное уравнение и преобразование является линейным. Это соответствует ситуации, когда одна из неподвижных точек - бесконечно удаленная точка. Когда а ≠ d вторая неподвижная точка конечна и определяется выражением

${ displaystyle gamma = - { frac {b} {a-d}}.}$

В этом случае преобразование будет простым преобразованием, состоящим из переводы, вращения, и расширение:

${ Displaystyle г mapsto альфа г + бета. ,}$

Если c = 0 и а = d, то обе неподвижные точки находятся на бесконечности, и преобразование Мёбиуса соответствует чистому переносу:

${ displaystyle z mapsto z + beta.}$

Топологическое доказательство

Топологически тот факт, что (неединичные) преобразования Мёбиуса фиксируют 2 точки (с кратностью), соответствует Эйлерова характеристика сферы равно 2:

${ displaystyle chi ({ hat { mathbf {C}}}) = 2.}$

Во-первых, проективная линейная группа PGL (2,K) является резко 3-переходный - для любых двух упорядоченных троек различных точек существует уникальное отображение, которое переводит одну тройку в другую, как и для преобразований Мёбиуса, и с помощью того же алгебраического доказательства (по существу подсчет размеров, поскольку группа трехмерна). Таким образом, любая карта, фиксирующая не менее 3 точек, является тождественной.

Далее, можно увидеть, отождествив группу Мёбиуса с ${ Displaystyle PGL (2, mathbb {C})}$ что любая функция Мёбиуса гомотопна тождеству. Действительно, любой член общая линейная группа может быть сведено к тождественному отображению методом исключения Гаусса-Жордана, это показывает, что проективная линейная группа также линейно связна, обеспечивая гомотопию тождественному отображению. В Теорема Лефшеца – Хопфа. утверждает, что сумма индексов (в данном контексте кратности) неподвижных точек карты с конечным числом неподвижных точек равна Число Лефшеца отображения, которое в данном случае является следом тождественного отображения на группах гомологий, которое является просто эйлеровой характеристикой.

Напротив, проективная линейная группа вещественной проективной прямой PGL (2,р) не нужно исправлять какие-либо точки - например, ${ Displaystyle (1 + х) / (1-х)}$ не имеет (реальных) неподвижных точек: как сложное преобразование фиксирует ±я^{[примечание 1]} - пока карта 2Икс фиксирует две точки 0 и ∞. Это соответствует тому факту, что эйлерова характеристика круга (действительной проективной прямой) равна 0, и, таким образом, теорема Лефшеца о неподвижной точке говорит только, что она должна фиксировать не менее 0 точек, но, возможно, и больше.

Нормальная форма

Преобразования Мёбиуса также иногда записываются через их неподвижные точки в так называемых нормальная форма. Сначала мы рассмотрим непараболический случай, когда есть две различные неподвижные точки.

Непараболический случай:

Каждое непараболическое преобразование сопрягать к растяжению / вращению, т. е. преобразованию формы

${ Displaystyle г mapsto kz ,}$

(k ∈ C) с неподвижными точками в 0 и ∞. Чтобы увидеть это, определите карту

${ Displaystyle г (z) = { гидроразрыва {z- gamma _ {1}} {z- gamma _ {2}}}}$

который отправляет точки (γ₁, γ₂) в (0, ∞). Здесь мы предполагаем, что γ₁ и γ₂ различны и конечны. Если один из них уже находится на бесконечности, то грамм можно изменить так, чтобы зафиксировать бесконечность и отправить другую точку на 0.

Если ж имеет различные неподвижные точки (γ₁, γ₂) то преобразование ${ displaystyle gfg ^ {- 1}}$ имеет неподвижные точки в 0 и ∞ и, следовательно, является растяжением: ${ displaystyle gfg ^ {- 1} (z) = kz}$. Уравнение неподвижной точки для преобразования ж тогда можно написать

${ Displaystyle { гидроразрыва {е (г) - гамма _ {1}} {е (г) - гамма _ {2}}} = к { гидроразрыва {г- гамма _ {1}} {г - gamma _ {2}}}.}$

Решение для ж дает (в матричной форме):

${ displaystyle { mathfrak {H}} (k; gamma _ {1}, gamma _ {2}) = { begin {pmatrix} gamma _ {1} -k gamma _ {2} & ( k-1) gamma _ {1} gamma _ {2} 1-k & k gamma _ {1} - gamma _ {2} end {pmatrix}}}$

или, если одна из неподвижных точек находится на бесконечности:

${ displaystyle { mathfrak {H}} (k; gamma, infty) = { begin {pmatrix} k & (1-k) gamma 0 & 1 end {pmatrix}}.}$

Из приведенных выше выражений можно вычислить производные от ж в фиксированных точках:

${ Displaystyle е '( гамма _ {1}) = к ,}$ и ${ Displaystyle е '( гамма _ {2}) = 1 / к. ,}$

Обратите внимание, что, учитывая порядок неподвижных точек, мы можем выделить один из множителей (k) из ж как характеристическая постоянная из ж. Изменение порядка неподвижных точек на противоположное эквивалентно взятию обратного множителя в качестве характеристической постоянной:

${ displaystyle { mathfrak {H}} (k; gamma _ {1}, gamma _ {2}) = { mathfrak {H}} (1 / k; gamma _ {2}, gamma _ {1}).}$

Для локсодромных преобразований, когда |k| > 1 говорят, что γ₁ это отталкивающий неподвижная точка, а γ₂ это привлекательный фиксированная точка. Для |k| <1, роли меняются.

Параболический случай:

В параболическом случае имеется только одна неподвижная точка γ. Преобразование, переводящее эту точку в ∞, есть

${ Displaystyle г (z) = { гидроразрыва {1} {z- gamma}}}$

или тождество, если γ уже на бесконечности. Преобразование ${ displaystyle gfg ^ {- 1}}$ фиксирует бесконечность и поэтому является переводом:

${ Displaystyle gfg ^ {- 1} (г) = г + бета ,.}$

Здесь β называется длина перевода. Тогда формула неподвижной точки для параболического преобразования имеет вид

${ displaystyle { frac {1} {f (z) - gamma}} = { frac {1} {z- gamma}} + beta.}$

Решение для ж (в матричной форме) дает

${ Displaystyle { mathfrak {H}} ( beta; gamma) = { begin {pmatrix} 1+ gamma beta & - beta gamma ^ {2} beta & 1- gamma beta end {pmatrix}}}$

или, если γ = ∞:

${ displaystyle { mathfrak {H}} ( beta; infty) = { begin {pmatrix} 1 & beta 0 & 1 end {pmatrix}}}$

Обратите внимание, что β - это нет характеристическая постоянная ж, который всегда равен 1 для параболического преобразования. Из приведенных выше выражений можно вычислить:

${ Displaystyle е '( гамма) = 1. ,}$

Полюса трансформации

Смысл ${ displaystyle z _ { infty} = - { frac {d} {c}}}$ называется столб из ${ displaystyle { mathfrak {H}}}$; это та точка, которая превращается в бесконечно удаленную точку при ${ displaystyle { mathfrak {H}}}$.

Обратный полюс ${ displaystyle Z _ { infty} = { frac {a} {c}}}$ - это точка, в которую преобразуется бесконечно удаленная точка. Точка на полпути между двумя полюсами всегда совпадает с точкой на полпути между двумя фиксированными точками:

${ displaystyle gamma _ {1} + gamma _ {2} = z _ { infty} + Z _ { infty}.}$

Эти четыре точки являются вершинами параллелограмм который иногда называют характерный параллелограмм трансформации.

Преобразование ${ displaystyle { mathfrak {H}}}$ можно задать с двумя неподвижными точками γ₁, γ₂ и полюс ${ displaystyle z _ { infty}}$.

${ displaystyle { mathfrak {H}} = { begin {pmatrix} Z _ { infty} & - gamma _ {1} gamma _ {2} 1 & -z _ { infty} end {pmatrix} }, ; ; Z _ { infty} = gamma _ {1} + gamma _ {2} -z _ { infty}.}$

Это позволяет нам вывести формулу для преобразования между k и ${ displaystyle z _ { infty}}$ данный ${ displaystyle gamma _ {1}, gamma _ {2}}$:

${ displaystyle z _ { infty} = { frac {k gamma _ {1} - gamma _ {2}} {1-k}}}$

${ displaystyle k = { frac { gamma _ {2} -z _ { infty}} { gamma _ {1} -z _ { infty}}} = { frac {Z _ { infty} - gamma _ {1}} {Z _ { infty} - gamma _ {2}}} = { frac {ac gamma _ {1}} {ac gamma _ {2}}},}$

что сводится к

${ displaystyle k = { frac {(a + d) + { sqrt {(ad) ^ {2} + 4bc}}} {(a + d) - { sqrt {(ad) ^ {2} + 4bc}}}}.}$

Последнее выражение совпадает с одним из (взаимно обратных) собственное значение соотношения ${ displaystyle lambda _ {1} over lambda _ {2}}$ матрицы

${ Displaystyle { mathfrak {H}} = { begin {pmatrix} a & b c & d end {pmatrix}}}$

представляющий преобразование (сравните обсуждение характеристической константы преобразования в предыдущем разделе). Его характеристический многочлен равно

${ displaystyle det ( lambda I_ {2} - { mathfrak {H}}) = lambda ^ {2} - operatorname {tr} { mathfrak {H}} , lambda + det { mathfrak {H}} = lambda ^ {2} - (a + d) lambda + (ad-bc)}$

который имеет корни

${ displaystyle lambda _ {i} = { frac {(a + d) pm { sqrt {(ad) ^ {2} + 4bc}}} {2}} = { frac {(a + d ) pm { sqrt {(a + d) ^ {2} -4 (ad-bc)}}} {2}} = c gamma _ {i} + d .}$

Простые преобразования Мёбиуса и композиция

Преобразование Мёбиуса может быть составлен как последовательность простых преобразований.

Следующие простые преобразования также являются преобразованиями Мёбиуса:

${ Displaystyle f (z) = z + b quad (a = 1, c = 0, d = 1)}$это перевод

${ displaystyle f (z) = az quad (b = 0, c = 0, d = 1)}$представляет собой комбинацию (гомотетия и вращение )Если ${ Displaystyle | а | = 1}$ то это вращение, если ${ Displaystyle а в mathbb {R}}$ тогда это гомотетия

${ displaystyle f (z) = 1 / z quad (a = 0, b = 1, c = 1, d = 0)}$ (инверсия и отражение относительно действительной оси)

Составление простых преобразований

Если ${ displaystyle c neq 0,}$ позволять:

• ${ displaystyle f_ {1} (z) = z + d / c quad}$ (перевод к d/c)
• ${ displaystyle f_ {2} (z) = 1 / z quad}$ (инверсия и отражение относительно действительной оси)
• ${ displaystyle f_ {3} (z) = { frac {bc-ad} {c ^ {2}}} z quad}$ (гомотетия и вращение )
• ${ displaystyle f_ {4} (z) = z + a / c quad}$ (перевод а/c)

Тогда эти функции можно составлен, давая

${ displaystyle f_ {4} circ f_ {3} circ f_ {2} circ f_ {1} (z) = f (z) = { frac {az + b} {cz + d}}.}$

То есть,

${ displaystyle { frac {az + b} {cz + d}} = { frac {a} {c}} + { frac {e} {z + { frac {d} {c}}}}, }$

с

${ displaystyle e = { frac {bc-ad} {c ^ {2}}}.}$

Это разложение делает очевидными многие свойства преобразования Мёбиуса.

Элементарные свойства

Преобразование Мёбиуса эквивалентно последовательности более простых преобразований. Композиция делает очевидными многие свойства преобразования Мёбиуса.

Формула обратного преобразования

Существование обратного преобразования Мёбиуса и его явная формула легко выводятся из композиции обратных функций более простых преобразований. То есть определить функции грамм₁, грамм₂, грамм₃, грамм₄ так что каждый грамм_я инверсия ж_я. Тогда композиция

${ displaystyle g_ {1} circ g_ {2} circ g_ {3} circ g_ {4} (z) = f ^ {- 1} (z) = { frac {dz-b} {- cz + а}}}$ дает формулу для обратного.

Сохранение углов и обобщенных окружностей

Из этого разложения мы видим, что преобразования Мёбиуса переносят все нетривиальные свойства инверсия круга. Например, сохранение углов сводится к доказательству того, что инверсия окружности сохраняет углы, поскольку другие типы преобразований - это растяжение и изометрии (перенос, отражение, вращение), которые тривиально сохраняют углы.

Кроме того, преобразования Мёбиуса отображают обобщенные круги к обобщенным окружностям, поскольку инверсия окружностей обладает этим свойством. Обобщенный круг - это либо круг, либо линия, последняя рассматривается как круг, проходящий через бесконечно удаленную точку. Обратите внимание, что преобразование Мёбиуса не обязательно отображает круги в окружности и линии в линии: оно может смешивать их. Даже если он сопоставляет круг с другим кругом, он не обязательно сопоставляет центр первого круга с центром второго круга.

Сохранение перекрестного отношения

Кросс-отношения инвариантны относительно преобразований Мёбиуса. То есть, если преобразование Мёбиуса отображает четыре различные точки ${ displaystyle z_ {1}, z_ {2}, z_ {3}, z_ {4}}$ до четырех различных точек ${ displaystyle w_ {1}, w_ {2}, w_ {3}, w_ {4}}$ соответственно, то

${ displaystyle { frac {(z_ {1} -z_ {3}) (z_ {2} -z_ {4})} {(z_ {2} -z_ {3}) (z_ {1} -z_ { 4})}} = { frac {(w_ {1} -w_ {3}) (w_ {2} -w_ {4})} {(w_ {2} -w_ {3}) (w_ {1} -w_ {4})}}.}$

Если одна из точек ${ displaystyle z_ {1}, z_ {2}, z_ {3}, z_ {4}}$ - бесконечно удаленная точка, тогда необходимо определить перекрестное отношение, взяв соответствующий предел; например перекрестное соотношение ${ displaystyle z_ {1}, z_ {2}, z_ {3}, infty}$ является

${ displaystyle { frac {(z_ {1} -z_ {3})} {(z_ {2} -z_ {3})}}.}.$

Поперечное отношение четырех разных точек реально тогда и только тогда, когда через них проходит линия или круг. Это еще один способ показать, что преобразования Мёбиуса сохраняют обобщенные окружности.

Конъюгация

Две точки z₁ и z₂ находятся сопрягать относительно обобщенного круга C, если по обобщенному кругу D проходя через z₁ и z₂ и резка C в двух точках а и б, (z₁, z₂; а, б) находятся в гармоническое поперечное отношение (т.е. их кросс-отношение равно -1). Это свойство не зависит от выбора круга. D. Это свойство также иногда называют симметричный относительно линии или круга.^[2][3]

Две точки z, z^∗ сопряжены относительно прямой, если они симметричный относительно линии. Две точки сопряжены относительно окружности, если они меняются местами инверсия относительно этого круга.

Смысл z^∗ сопрягать с z когда L линия определяется вектором на основе е^iθ в момент z₀ может быть явно задан как

${ displaystyle z ^ {*} = e ^ {2i theta} { overline {z-z_ {0}}} + z_ {0}.}$

Смысл z^∗ сопрягать с z когда C круг радиуса р по центру z₀ может быть явно задан как

${ displaystyle z ^ {*} = { frac {r ^ {2}} { overline {z-z_ {0}}}} + z_ {0}}$

Поскольку преобразования Мёбиуса сохраняют обобщенные окружности и кросс-отношения, они сохраняют также сопряжение.

Представления проективных матриц

Естественный действие PGL (2,C) на сложная проективная линия CP¹ в точности естественное действие группы Мёбиуса на сфере Римана, где проективная прямая CP¹ и сфера Римана идентифицируются следующим образом:

${ displaystyle [z_ {1}: z_ {2}] Thicksim [z_ {1} / z_ {2}, 1].}$

Здесь [z₁:z₂] находятся однородные координаты на CP¹; точка [1: 0] соответствует точке ∞ сферы Римана. Используя однородные координаты, можно упростить многие конкретные вычисления с использованием преобразований Мёбиуса, так как не требуется различать регистр, связанный с ∞.

С каждым обратимый комплексная матрица 2 на 2

${ Displaystyle { mathfrak {H}} = { begin {pmatrix} a & c b & d end {pmatrix}}}$

мы можем сопоставить преобразование Мёбиуса

${ displaystyle [z, 1] { begin {pmatrix} a & c b & d end {pmatrix}} = [az + b, cz + d] = left [{ frac {az + b} {cz + d}}, 1 right] = f (z).}$

Условие объявление − до н.э ≠ 0 равносильно условию, что детерминант матрицы выше не равна нулю, т.е. матрица обратима.

Несложно проверить, что тогда товар двух матриц будет ассоциироваться с композицией двух соответствующих преобразований Мёбиуса. Другими словами, карта

${ displaystyle pi двоеточие OperatorName {GL} (2, mathbf {C}) to operatorname {Aut} ({ widehat { mathbf {C}}})}$

от общая линейная группа GL (2,C) в группу Мёбиуса, которая переводит матрицу ${ displaystyle { mathfrak {H}}}$ к преобразованию ж, это групповой гомоморфизм.

Обратите внимание, что любая матрица, полученная умножением ${ displaystyle { mathfrak {H}}}$ комплексным скаляром λ определяет то же преобразование, поэтому преобразование Мёбиуса определяет только свою матрицу вплоть до скалярные кратные. Другими словами: ядро из π состоит из всех скалярных кратных единичная матрица я, а первая теорема об изоморфизме теории групп утверждает, что факторгруппа GL (2,C) / ((С {0})я) изоморфна группе Мёбиуса. Эта фактор-группа известна как проективная линейная группа и обычно обозначается PGL (2,C).

${ displaystyle operatorname {Aut} ({ widehat { mathbf {C}}}) cong operatorname {PGL} (2, mathbf {C}).}$

Такая же идентификация PGL (2,K) с группой дробно-линейных преобразований и с группой проективных линейных автоморфизмов проективной прямой выполняется над любым полем K, факт, представляющий алгебраический интерес, особенно для конечных полей, хотя случай комплексных чисел представляет наибольший геометрический интерес.

Если кто-то ограничивает ${ displaystyle { mathfrak {H}}}$ матрицам детерминантной, отображение π ограничивается сюръективным отображением из специальная линейная группа SL (2,C) группе Мёбиуса; в ограниченном случае ядро ​​состоит из плюс и минус единицы, а фактор-группа SL (2,C) / {±я}, обозначаемый PSL (2,C), следовательно, также изоморфна группе Мёбиуса:

${ displaystyle operatorname {Aut} ({ widehat { mathbf {C}}}) cong operatorname {PSL} (2, mathbf {C}).}$

Отсюда мы видим, что группа Мёбиуса является 3-мерной комплексной группой Ли (или 6-мерной действительной группой Ли). Это полупростой не-компактный Группа Ли.

Обратите внимание, что существует ровно две матрицы с единичным определителем, которые можно использовать для представления любого данного преобразования Мёбиуса. То есть SL (2,C) это двойная крышка PSL (2,C). Поскольку SL (2,C) является односвязный это универсальный чехол группы Мёбиуса. Следовательно фундаментальная группа группы Мёбиуса Z₂.

Задание преобразования по трем точкам

Учитывая набор из трех различных точек z₁, z₂, z₃ на сфере Римана и второй набор различных точек ш₁, ш₂, ш₃, существует ровно одно преобразование Мёбиуса ж(z) с ж(z_я) = ш_я за я = 1,2,3. (Другими словами: действие группы Мёбиуса на сфере Римана есть резко 3-переходный.) Есть несколько способов определить ж(z) из заданных наборов точек.

Отображение сначала на 0, 1, ∞

Легко проверить, что преобразование Мёбиуса

${ displaystyle f_ {1} (z) = { frac {(z-z_ {1}) (z_ {2} -z_ {3})} {(z-z_ {3}) (z_ {2} - z_ {1})}}}$

с матрицей

${ displaystyle { mathfrak {H}} _ {1} = { begin {pmatrix} z_ {2} -z_ {3} & - z_ {1} (z_ {2} -z_ {3}) z_ {2} -z_ {1} & - z_ {3} (z_ {2} -z_ {1}) end {pmatrix}}}$

карты z₁, z₂, z₃ до 0, 1, ∞ соответственно. Если один из z_я равно ∞, то правильная формула для ${ displaystyle { mathfrak {H}} _ {1}}$ получается из приведенного выше, сначала разделив все записи на z_я а затем взяв предел z_я → ∞.

Если ${ displaystyle { mathfrak {H}} _ {2}}$ аналогично определяется для map ш₁, ш₂, ш₃ до 0, 1, ∞, то матрица ${ displaystyle { mathfrak {H}}}$ который отображает z_1,2,3 к ш_1,2,3 становится

${ displaystyle { mathfrak {H}} = { mathfrak {H}} _ {2} ^ {- 1} { mathfrak {H}} _ {1}.}$

Стабилизатор {0, 1, ∞} (как неупорядоченного множества) - это подгруппа, известная как ангармоническая группа.

Явная детерминантная формула

Уравнение

${ displaystyle w = { frac {az + b} {cz + d}}}$

эквивалентно уравнению эталона гипербола

${ displaystyle , cwz-az + dw-b = 0}$

в (z,ш)-самолет. Проблема построения преобразования Мёбиуса ${ Displaystyle { mathfrak {H}} (г)}$ отображение тройки ${ displaystyle (z_ {1}, z_ {2}, z_ {3})}$ к другой тройке ${ displaystyle (w_ {1}, w_ {2}, w_ {3})}$ таким образом, эквивалентно нахождению коэффициентов а, б, c, d гиперболы, проходящей через точки ${ displaystyle (z_ {i}, w_ {i})}$. Явное уравнение можно найти, оценив детерминант

${ displaystyle det { begin {pmatrix} zw & z & w & 1 z_ {1} w_ {1} & z_ {1} & w_ {1} & 1 z_ {2} w_ {2} & z_ {2} & w_ {2} & 1 z_ {3} w_ {3} & z_ {3} & w_ {3} & 1 end {pmatrix}} ,}$

с помощью Разложение лапласа по первому ряду. Это приводит к детерминантным формулам

${ displaystyle a = det { begin {pmatrix} z_ {1} w_ {1} & w_ {1} & 1 z_ {2} w_ {2} & w_ {2} & 1 z_ {3} w_ {3 } & w_ {3} & 1 end {pmatrix}} ,}$

${ displaystyle b = det { begin {pmatrix} z_ {1} w_ {1} & z_ {1} & w_ {1} z_ {2} w_ {2} & z_ {2} & w_ {2} z_ {3} w_ {3} & z_ {3} & w_ {3} end {pmatrix}} ,}$

${ displaystyle c = det { begin {pmatrix} z_ {1} & w_ {1} & 1 z_ {2} & w_ {2} & 1 z_ {3} & w_ {3} & 1 end {pmatrix}} ,}$

${ displaystyle d = det { begin {pmatrix} z_ {1} w_ {1} & z_ {1} & 1 z_ {2} w_ {2} & z_ {2} & 1 z_ {3} w_ {3 } & z_ {3} & 1 end {pmatrix}}}$

для коэффициентов а, б, в, г представляющей матрицы ${ Displaystyle , { mathfrak {H}} = { begin {pmatrix} a & b c & d end {pmatrix}}}$. Построенная матрица ${ displaystyle { mathfrak {H}}}$ имеет определитель, равный ${ displaystyle (z_ {1} -z_ {2}) (z_ {1} -z_ {3}) (z_ {2} -z_ {3}) (w_ {1} -w_ {2}) (w_ { 1} -w_ {3}) (w_ {2} -w_ {3})}$ который не исчезает, если z_я соотв. ш_я попарно различны, поэтому преобразование Мёбиуса корректно. Если одна из точек z_я или же ш_я равно ∞, то сначала делим все четыре определителя на эту переменную, а затем берем предел, когда переменная приближается к ∞.

Подгруппы группы Мёбиуса

Если нам потребуются коэффициенты а, б, c, d преобразования Мёбиуса в действительные числа с объявление − до н.э = 1, получаем подгруппу группы Мёбиуса, обозначенную как PSL (2,р). Это группа преобразований Мёбиуса, отображающих верхняя полуплоскость ЧАС = Икс + яу : у > 0 самому себе, и равен группе всех биголоморфный (или эквивалентно: биективный, конформный и сохраняющие ориентацию) карты ЧАС → ЧАС. Если правильно метрика вводится, верхняя полуплоскость становится моделью гиперболическая плоскость ЧАС², то Модель полуплоскости Пуанкаре, и PSL (2,р) - группа всех сохраняющих ориентацию изометрий ЧАС² в этой модели.

Подгруппа всех преобразований Мёбиуса, отображающих открытый диск D = z : |z| < 1 в себя состоит из всех преобразований вида

${ displaystyle f (z) = e ^ {i phi} { frac {z + b} {{ bar {b}} z + 1}}}$

с ${ displaystyle phi}$ ∈ р, б ∈ C и |б| <1. Это равно группе всех биголоморфных (или эквивалентно: биективных, сохраняющих угол и сохраняющих ориентацию) отображений D → D. При введении подходящей метрики открытый диск превращается в другую модель гиперболической плоскости - Модель диска Пуанкаре, и эта группа является группой всех сохраняющих ориентацию изометрий ЧАС² в этой модели.

Поскольку обе указанные выше подгруппы служат группами изометрий ЧАС², они изоморфны. Конкретный изоморфизм дается формулой спряжение с преобразованием

${ Displaystyle е (г) = { гидроразрыва {г + я} {из + 1}}}$

который биективно отображает открытый единичный диск в верхнюю полуплоскость.

В качестве альтернативы рассмотрим открытый диск с радиусом р, с центром в р я. Модель диска Пуанкаре в этом диске становится идентичной модели верхней полуплоскости как р приближается к ∞.

А максимальная компактная подгруппа группы Мебиуса ${ Displaystyle { mathcal {M}}}$ дан кем-то (Tóth 2002 )^[4]

${ displaystyle { mathcal {M}} _ {0}: = left {z mapsto { frac {uz - { bar {v}}} {vz + { bar {u}}}}: | u | ^ {2} + | v | ^ {2} = 1 right },}$

и соответствует при изоморфизме ${ Displaystyle { mathcal {M}} cong operatorname {PSL} (2, mathbf {C})}$ к проективная специальная унитарная группа БП (2,C), который изоморфен специальная ортогональная группа SO (3) вращений в трех измерениях, и может быть интерпретировано как вращение сферы Римана. Каждая конечная подгруппа сопряжена с этой максимальной компактной группой, и, следовательно, они точно соответствуют группам полиэдров, т.е. группы точек в трех измерениях.

Икосаэдрические группы преобразований Мёбиуса использовались Феликс Кляйн дать аналитическое решение уравнение пятой степени в (Кляйн 1888 ); современная экспозиция представлена ​​в (Tóth 2002 ).^[5]

Если нам потребуются коэффициенты а, б, c, d преобразования Мёбиуса быть целые числа с объявление − до н.э = 1, получаем модульная группа PSL (2,Z), дискретная подгруппа в PSL (2,р) важно при изучении решетки в комплексной плоскости, эллиптические функции и эллиптические кривые. Дискретные подгруппы PSL (2,р) известны как Фуксовы группы; они важны при изучении Римановы поверхности.

Классификация

Показано гиперболическое преобразование. Предварительные изображения единичного круга круги Аполлония с соотношением расстояний c/а и фокусы на -б/а и -d/c .

По тем же очагам -б/а и -d/c красные круги соответствуют лучам, проходящим через начало координат.

В следующем обсуждении мы всегда будем предполагать, что представляющая матрица ${ displaystyle { mathfrak {H}}}$ нормализована так, что ${ Displaystyle Det { mathfrak {H}} = ad-bc = 1}$.

Нетождественные преобразования Мёбиуса обычно делятся на четыре типа: параболический, эллиптический, гиперболический и локсодромный, причем гиперболические являются подклассом локсодромных. Классификация имеет как алгебраическое, так и геометрическое значение. Геометрически различные типы приводят к различным преобразованиям комплексной плоскости, как показано на рисунках ниже.

Эти четыре типа можно различить, посмотрев на след ${ displaystyle operatorname {tr} , { mathfrak {H}} = a + d}$. Отметим, что след инвариантен относительно спряжение, то есть,

${ displaystyle operatorname {tr} , { mathfrak {GHG}} ^ {- 1} = operatorname {tr} , { mathfrak {H}},}$

и поэтому каждый член класса сопряженности будет иметь один и тот же след. Любое преобразование Мёбиуса можно записать так, чтобы его представляющая матрица ${ displaystyle { mathfrak {H}}}$ имеет определитель один (путем умножения элементов на подходящий скаляр). Два преобразования Мебиуса ${ displaystyle { mathfrak {H}}, { mathfrak {H}} '}$ (оба не равны тождественному преобразованию) с ${ Displaystyle Det { mathfrak {H}} = Det { mathfrak {H}} '= 1}$ сопряжены тогда и только тогда, когда ${ displaystyle operatorname {tr} ^ {2} , { mathfrak {H}} = operatorname {tr} ^ {2} , { mathfrak {H}} '.}$

Параболические преобразования

Нетождественное преобразование Мёбиуса, заданное матрицей ${ displaystyle { mathfrak {H}}}$ детерминанта один называется параболический если

${ displaystyle operatorname {tr} ^ {2} { mathfrak {H}} = (a + d) ^ {2} = 4}$

(так что след равен плюс или минус 2; любое из них может произойти для данного преобразования, поскольку ${ displaystyle { mathfrak {H}}}$ определяется только до подписи). Фактически, один из вариантов ${ displaystyle { mathfrak {H}}}$ имеет то же самое характеристический многочлен Икс²−2Икс+1 как единичная матрица, и поэтому всесильный. Преобразование Мёбиуса является параболическим тогда и только тогда, когда оно имеет ровно одну неподвижную точку в расширенная комплексная плоскость ${ displaystyle { widehat { mathbf {C}}} = mathbf {C} cup { infty }}$, что происходит тогда и только тогда, когда его можно определить матрицей сопрягать с

${ displaystyle { begin {pmatrix} 1 & 1 0 & 1 end {pmatrix}}}$

который описывает перевод в комплексной плоскости.

Множество всех параболических преобразований Мёбиуса с данный фиксированная точка в ${ displaystyle { widehat { mathbf {C}}}}$вместе с идентичностью образует подгруппа изоморфна группе матриц

${ displaystyle left {{ begin {pmatrix} 1 & b 0 & 1 end {pmatrix}} mid b in mathbf {C} right };}$

это пример унипотентный радикал из Подгруппа Бореля (группы Мёбиуса или SL (2,C) для группы матриц; понятие определено для любого редуктивная группа Ли ).

Характеристическая константа

Все непараболические преобразования имеют две неподвижные точки и определяются матрицей, сопряженной с

${ displaystyle { begin {pmatrix} lambda & 0 0 & lambda ^ {- 1} end {pmatrix}}}$

с комплексным числом λ, не равным 0, 1 или −1, что соответствует растяжению / повороту посредством умножения на комплексное число k = λ², называется характеристическая постоянная или же множитель трансформации.

Эллиптические преобразования

В Диаграмма Смита, использован инженеры-электрики для анализа линии передачи, представляет собой визуальное изображение эллиптического преобразования Мёбиуса Γ= (г-1) / (г + 1). Каждая точка на диаграмме Смита одновременно представляет собой значение z (внизу слева) и соответствующее значение Γ (внизу справа) для | Γ | <1.

Преобразование называется эллиптический если его можно представить в виде матрицы ${ displaystyle { mathfrak {H}}}$ чей след настоящий с

${ Displaystyle 0 Leq OperatorName {tr} ^ {2} { mathfrak {H}} <4. ,}$

Преобразование является эллиптическим тогда и только тогда, когда | λ | = 1 и λ ≠ ± 1. Письмо ${ Displaystyle лямбда = е ^ {я альфа}}$, эллиптическое преобразование сопряжено с

${ displaystyle { begin {pmatrix} cos alpha & - sin alpha sin alpha & cos alpha end {pmatrix}}}$

с α вещественным.

Обратите внимание, что для любой ${ displaystyle { mathfrak {H}}}$ с характеристической постоянной k, характеристическая постоянная ${ Displaystyle { mathfrak {H}} ^ {п}}$ является k^п. Таким образом, все преобразования Мёбиуса конечных порядок являются эллиптическими преобразованиями, а именно такими, в которых λ - корень единства, или, что то же самое, где α - рациональный несколько из π. Простейшая возможность дробного кратного среднего α = π/ 2, что также является уникальным случаем ${ displaystyle operatorname {tr} { mathfrak {H}} = 0}$, также обозначается как круговое преобразование; геометрически это соответствует повороту на 180 ° вокруг двух фиксированных точек. Этот класс представлен в матричной форме как:

${ displaystyle { begin {pmatrix} 0 & -1 1 & 0 end {pmatrix}}.}$

Есть 3 представителя, фиксирующие {0, 1, ∞}, которые являются тремя транспозициями в группе симметрии этих 3 точек: ${ displaystyle 1 / z,}$ который исправляет 1 и меняет местами 0 на ∞ (поворот на 180 ° вокруг точек 1 и −1), ${ displaystyle 1-z}$, который исправляет ∞ и меняет местами 0 на 1 (поворот на 180 ° вокруг точек 1/2 и ∞), и ${ Displaystyle Z / (Z-1)}$ который исправляет 0 и меняет местами 1 на ∞ (поворот на 180 ° относительно точек 0 и 2).

Гиперболические преобразования

Преобразование называется гиперболический если его можно представить в виде матрицы ${ displaystyle { mathfrak {H}}}$ чей след настоящий с

${ displaystyle operatorname {tr} ^ {2} { mathfrak {H}}> 4. ,}$

Преобразование гиперболично тогда и только тогда, когда λ вещественно и λ ≠ ± 1.

Локсодромные преобразования

Преобразование называется локсодромный если ${ displaystyle operatorname {tr} ^ {2} { mathfrak {H}}}$ нет в [0,4]. Преобразование локсодромно тогда и только тогда, когда ${ displaystyle | lambda | neq 1}$.

Исторически, навигация к локсодромия или же линия румба относится к пути постоянного несущий; полученный путь - это логарифмическая спираль, по форме похожее на преобразования комплексной плоскости, выполняемые локсодромным преобразованием Мёбиуса. См. Геометрические фигуры ниже.

Основная классификация

Трансформация	Квадрат следа	Множители	Представитель класса
Круговой	σ = 0	k = −1	${ displaystyle { begin {pmatrix} i & 0 0 & -i end {pmatrix}}}$	z ↦ −z
Эллиптический	0 ≤ σ <4	|k| = 1 ${ Displaystyle к = е ^ { пм я тета} neq 1}$	${ displaystyle { begin {pmatrix} e ^ {i theta / 2} & 0 0 & e ^ {- i theta / 2} end {pmatrix}}}$	z ↦ еяθ z
Параболический	σ = 4	k = 1	${ displaystyle { begin {pmatrix} 1 & a 0 & 1 end {pmatrix}}}$	z ↦ z + а
Гиперболический	4 <σ <∞	${ Displaystyle к ин mathbf {R} ^ {+}}$ ${ Displaystyle к = е ^ { пм тета} neq 1}$	${ displaystyle { begin {pmatrix} e ^ { theta / 2} & 0 0 & e ^ {- theta / 2} end {pmatrix}}}$	z ↦ еθ z
Локсодромный	σ ∈ C \ [0,4]	${ Displaystyle | к | neq 1}$ ${ Displaystyle к = лямбда ^ {2}, лямбда ^ {- 2}}$	${ displaystyle { begin {pmatrix} lambda & 0 0 & lambda ^ {- 1} end {pmatrix}}}$	z ↦ kz

Реальный случай и примечание по терминологии

Для действительных чисел (если коэффициенты должны быть действительными) нет негиперболических локсодромических преобразований, а классификация делится на эллиптические, параболические и гиперболические, как для действительных чисел. коники. Терминология основана на рассмотрении половины абсолютного значения трассы, | tr | / 2, как эксцентриситет преобразования - деление на 2 исправляет размер, поэтому тождество имеет эксцентриситет 1 (tr /п иногда используется в качестве альтернативы для трассы по этой причине), а абсолютное значение корректирует только для трассы, определенной с коэффициентом ± 1 из-за работы в PSL. В качестве альтернативы можно использовать половину следа в квадрате в качестве прокси для квадрата эксцентриситета, как это было сделано выше; эти классификации (но не точные значения эксцентриситета, поскольку квадраты и абсолютные значения различны) совпадают для реальных трасс, но не для сложных трасс. Та же терминология используется для классификация элементов SL (2, р) (2-кратная обложка) и аналогичные классификации используются в других местах. Локсодромные превращения - это по существу сложное явление и соответствуют сложным эксцентриситетам.

Геометрическая интерпретация характеристической постоянной

На следующем рисунке изображены (после стереографического преобразования сферы в плоскость) две неподвижные точки преобразования Мёбиуса в непараболическом случае:

Характеристическая постоянная может быть выражена через ее логарифм:

${ Displaystyle е ^ { ро + альфа я} = к. ;}$

При таком выражении действительное число ρ становится коэффициентом расширения. Он показывает, насколько отталкивающая неподвижная точка γ₁ есть, и насколько привлекательно γ₂ является. Действительное число α является коэффициентом поворота, показывающим, до какой степени преобразование поворачивает плоскость против часовой стрелки вокруг γ.₁ и по часовой стрелке около γ₂.

Эллиптические преобразования

Если ρ = 0, то неподвижные точки не являются ни притягивающими, ни отталкивающими, а безразличными, и преобразование называется эллиптический. Эти преобразования имеют тенденцию перемещать все точки по кругу вокруг двух фиксированных точек. Если одна из неподвижных точек находится на бесконечности, это эквивалентно аффинному вращению вокруг точки.

Если мы возьмем однопараметрическая подгруппа порожденный любым эллиптическим преобразованием Мёбиуса, мы получаем непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одно и тоже два очка. Все остальные точки проходят по семейству окружностей, вложенных между двумя неподвижными точками на сфере Римана. В общем, две неподвижные точки могут быть любыми двумя разными точками.

У этого есть важная физическая интерпретация. Представьте, что какой-то наблюдатель вращается с постоянной угловой скоростью вокруг некоторой оси. Тогда мы можем принять две фиксированные точки за северный и южный полюса небесной сферы. Внешний вид ночного неба теперь непрерывно трансформируется точно так же, как это описывается однопараметрической подгруппой эллиптических преобразований, разделяющей фиксированные точки 0, ∞, и с числом α, соответствующим постоянной угловой скорости нашего наблюдателя.

Вот несколько рисунков, иллюстрирующих влияние эллиптического преобразования Мёбиуса на сферу Римана (после стереографической проекции на плоскость):

Эти изображения иллюстрируют эффект одного преобразования Мёбиуса. Однопараметрическая подгруппа, которую он генерирует непрерывно перемещает точки вдоль семейства дуг окружности, предложенных рисунками.

Гиперболические преобразования

Если α равно нулю (или кратно 2π), то преобразование называется гиперболический. Эти преобразования имеют тенденцию перемещать точки по круговым траекториям от одной фиксированной точки к другой.

Если мы возьмем однопараметрическая подгруппа порожденный любым гиперболическим преобразованием Мёбиуса, мы получаем непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одно и тоже два очка. Все остальные точки текут по определенному семейству дуг окружности. прочь от первой фиксированной точки и к вторая фиксированная точка. В общем, две неподвижные точки могут быть любыми двумя разными точками на сфере Римана.

Это тоже имеет важное физическое толкование. Представьте себе, что наблюдатель ускоряется (с постоянной величиной ускорения) в направлении северного полюса своей небесной сферы. Затем внешний вид ночного неба преобразуется точно так же, как описывается однопараметрической подгруппой гиперболических преобразований, разделяющих фиксированные точки 0, ∞, с действительным числом ρ, соответствующим величине его вектора ускорения. Кажется, что звезды движутся по долготе от Южного полюса к Северному полюсу. (Долготы выглядят как дуги окружности при стереографической проекции от сферы на плоскость.)

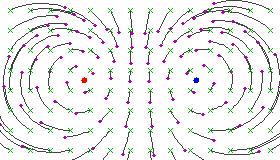
Вот несколько рисунков, иллюстрирующих влияние гиперболического преобразования Мёбиуса на сферу Римана (после стереографической проекции на плоскость):

Эти изображения напоминают силовые линии положительного и отрицательного электрического заряда, расположенные в фиксированных точках, потому что круговые линии потока образуют постоянный угол между двумя фиксированными точками.

Локсодромные превращения

Если и ρ, и α отличны от нуля, то преобразование называется локсодромный. Эти преобразования имеют тенденцию перемещать все точки на S-образных траекториях от одной фиксированной точки к другой.

Слово "локсодромия "от греческого:" λοξος (лохос), косой + δρόμος (дромос), курс". Когда парусный спорт на постоянной несущий - если вы держите курс (скажем) на северо-восток, вы в конечном итоге обойдете Северный полюс в логарифмическая спираль. На проекция меркатора такой курс - прямая линия, поскольку северный и южный полюса уходят в бесконечность. Угол, который образует локсодромия относительно линий долготы (т.е. ее наклон, «плотность» спирали), является аргументом k. Конечно, преобразования Мёбиуса могут иметь две фиксированные точки где угодно, а не только на северном и южном полюсах. Но любое локсодромное преобразование будет сопряжено с преобразованием, которое перемещает все точки вдоль таких локсодромов.

Если мы возьмем однопараметрическая подгруппа порожденный любым локсодромным преобразованием Мёбиуса, мы получаем непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одно и тоже два очка. Все остальные точки текут по определенному семейству кривых, прочь от первой фиксированной точки и к вторая фиксированная точка. В отличие от гиперболического случая, эти кривые являются не дугами окружности, а определенными кривыми, которые при стереографической проекции со сферы на плоскость выглядят как спиральные кривые, которые бесконечно часто вращаются против часовой стрелки вокруг одной фиксированной точки и бесконечно часто вращаются по часовой стрелке вокруг другой фиксированной точки. В общем, две неподвижные точки могут быть любыми двумя разными точками на сфере Римана.

Вы, вероятно, можете догадаться о физической интерпретации в случае, когда две фиксированные точки равны 0, ∞: наблюдатель, который одновременно вращается (с постоянной угловой скоростью) вокруг некоторой оси и движется вдоль одно и тоже ось, увидит появление преобразования ночного неба в соответствии с однопараметрической подгруппой локсодромных преобразований с фиксированными точками 0, ∞ и с ρ, α, определяемыми соответственно величиной фактических линейной и угловой скоростей.

Стереографическая проекция

Эти изображения показывают преобразования Мёбиуса стереографически спроектированный на Сфера Римана. В частности, обратите внимание, что при проецировании на сферу особый случай неподвижной точки на бесконечности ничем не отличается от наличия неподвижных точек в произвольном месте.

Одна неподвижная точка на бесконечности
Эллиптический	Гиперболический	Локсодромный
Точки крепления диаметрально противоположные
Эллиптический	Гиперболический	Локсодромный
Неподвижные точки в произвольном месте
Эллиптический	Гиперболический	Локсодромный

Итерация преобразования

Если преобразование ${ displaystyle { mathfrak {H}}}$ имеет неподвижные точки γ₁, γ₂, а характеристическая постоянная k, тогда ${ Displaystyle { mathfrak {H}} '= { mathfrak {H}} ^ {n}}$ буду иметь ${ Displaystyle gamma _ {1} '= gamma _ {1}, gamma _ {2}' = gamma _ {2}, k '= k ^ {n}}$.

Это можно использовать для повторять преобразование или оживить его, разбив его на шаги.

На этих изображениях показаны три точки (красная, синяя и черная), которые непрерывно повторяются при преобразованиях с различными характеристическими константами.

И эти изображения демонстрируют, что происходит, когда вы преобразуете круг с помощью гиперболических, эллиптических и локсодромных преобразований. Обратите внимание, что на эллиптических и локсодромных изображениях значение α равно 1/10.

Высшие измерения

В более высоких измерениях Преобразование Мёбиуса это гомеоморфизм из ${ displaystyle { overline { mathbb {R} ^ {n}}}}$, то одноточечная компактификация из ${ Displaystyle mathbb {R} ^ {п}}$, который представляет собой конечную композицию инверсии в сферах и размышления в гиперплоскости.^[6] Теорема Лиувилля в конформной геометрии утверждает, что по крайней мере в трех измерениях все конформный преобразования - это преобразования Мёбиуса. Любое преобразование Мёбиуса можно представить в виде

${ displaystyle f (x) = b + { frac { alpha A (x-a)} {| x-a | ^ { epsilon}}}}}$

куда ${ displaystyle a, b in mathbb {R} ^ {n}}$, ${ displaystyle alpha in mathbb {R}}$, ${ displaystyle A}$ является ортогональная матрица, и ${ displaystyle epsilon}$ равно 0 или 2. Группа преобразований Мёбиуса также называется Группа Мебиуса.^[7]

Сохраняющие ориентацию преобразования Мёбиуса образуют связную компоненту тождества в группе Мёбиуса. В измерении п = 2, сохраняющие ориентацию преобразования Мёбиуса - это в точности те отображения сферы Римана, которые здесь рассматриваются. Обращающие ориентацию получаются из них комплексным сопряжением.^[8]

Область преобразований Мёбиуса, т.е. ${ displaystyle { overline { mathbb {R} ^ {n}}}}$, гомеоморфно п-мерная сфера ${ Displaystyle S ^ {п}}$. Канонический изоморфизм между этими двумя пространствами - это Преобразование Кэли, которое само является преобразованием Мёбиуса ${ displaystyle { overline { mathbb {R} ^ {n + 1}}}}$. Это отождествление означает, что преобразования Мёбиуса также можно рассматривать как конформные изоморфизмы ${ Displaystyle S ^ {п}}$. В п-сфера вместе с действием группы Мёбиуса является геометрической структурой (в смысле теории Клейна). Программа Эрланген ) называется Геометрия Мёбиуса.^[9]

Приложения

Преобразование Лоренца

Изоморфизм группы Мёбиуса с Группа Лоренца был отмечен несколькими авторами: На основании предыдущей работы Феликс Кляйн (1893, 1897)^[10] на автоморфные функции связанные с гиперболической геометрией и геометрией Мёбиуса, Густав Херглотц (1909)^[11] показало, что гиперболические движения (т.е. изометрический автоморфизмы из гиперболическое пространство ) преобразование единичная сфера в себя соответствуют преобразованиям Лоренца, с помощью которых Герглотц смог классифицировать однопараметрические преобразования Лоренца на локсодромные, эллиптические, гиперболические и параболические группы. Другие авторы включают Эмиль Артин (1957),^[12] Х. С. М. Коксетер (1965),^[13] и Роджер Пенроуз, Вольфганг Риндлер (1984)^[14] и В. М. Оливия (2002)^[15]

Пространство Минковского состоит из четырехмерного реального координатного пространства р⁴ состоящее из пространства упорядоченных четверок (Икс₀,Икс₁,Икс₂,Икс₃) действительных чисел вместе с квадратичная форма

${ displaystyle Q (x_ {0}, x_ {1}, x_ {2}, x_ {3}) = x_ {0} ^ {2} -x_ {1} ^ {2} -x_ {2} ^ { 2} -x_ {3} ^ {2}.}$

Заимствование терминологии из специальная теория относительности, точки с Q > 0 считаются подобный времени; кроме того, если Икс₀ > 0, то точка называется указывающий на будущее. Очки с Q <0 называются космический. В нулевой конус S состоит из тех точек, где Q = 0; в будущий нулевой конус N⁺ те точки на нулевом конусе с Икс₀ > 0. небесная сфера затем отождествляется с набором лучей в N⁺ чья начальная точка является началом р⁴. Коллекция линейные преобразования на р⁴ с положительным детерминант сохраняя квадратичную форму Q и сохраняя направление времени от ограниченная группа Лоренца ТАК⁺(1,3).

В связи с геометрией небесной сферы группа преобразований SO⁺(1,3) отождествляется с группой PSL (2,C) преобразований Мёбиуса сферы. Для каждого (Икс₀,Икс₁,Икс₂,Икс₃) ∈ р⁴, связать эрмитова матрица

${ displaystyle X = { begin {bmatrix} x_ {0} + x_ {1} & x_ {2} + ix_ {3} x_ {2} -ix_ {3} & x_ {0} -x_ {1} конец {bmatrix}}.}$

В детерминант матрицы Икс равно Q(Икс₀,Икс₁,Икс₂,Икс₃). В специальная линейная группа действует на пространстве таких матриц посредством

${ Displaystyle X mapsto AXA ^ {*}}$

(1)

для каждого А ∈ SL (2,C), и это действие SL (2,C) сохраняет определитель Икс потому что Det А = 1. Поскольку определитель Икс отождествляется с квадратичной формой Q, SL (2,C) действует преобразованиями Лоренца. По размерным соображениям SL (2,C) покрывает окрестность единицы SO (1,3). Поскольку SL (2,C) связно, покрывает всю ограниченную группу Лоренца SO⁺(1,3). Кроме того, поскольку ядро действия (1) - подгруппа {±я}, затем переходя к факторгруппа дает групповой изоморфизм

${ displaystyle operatorname {PSL} (2, mathbf {C}) cong SO ^ {+} (1,3).}$

(2)

Обращаем внимание на случай, когда (Икс₀,Икс₁,Икс₂,Икс₃) равна нулю, матрица Икс имеет нулевой определитель и, следовательно, расщепляется как внешний продукт комплексного двумерного вектора ξ с его комплексно сопряженным:

${ Displaystyle X = xi { bar { xi}} ^ {T} = xi xi ^ {*}.}$

(3)

На двухкомпонентный вектор ξ действует SL (2,C) способом, совместимым с (1). Теперь ясно, что ядро ​​представления SL (2,C) на эрмитовых матрицах есть {±я}.

Действие PSL (2,C) на небесной сфере также можно описать геометрически с помощью стереографическая проекция. Рассмотрим сначала гиперплоскость в р⁴ данный Икс₀ = 1. Небесную сферу можно отождествить со сферой S⁺ пересечения гиперплоскости с будущим нулевым конусом N⁺. Стереографическая проекция с северного полюса (1,0,0,1) этой сферы на плоскость Икс₃ = 0 берет точку с координатами (1,Икс₁,Икс₂,Икс₃) с

${ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} = 1}$

к точке

${ displaystyle left (1, { frac {x_ {1}} {1-x_ {3}}}, { frac {x_ {2}} {1-x_ {3}}}, 0 right)) .}$

Представляем сложный координировать

${ displaystyle zeta = { frac {x_ {1} + ix_ {2}} {1-x_ {3}}},}$

обратная стереографическая проекция дает следующую формулу для точки (Икс₁, Икс₂, Икс₃) на S⁺:

${ displaystyle { begin {align} x_ {1} & = { frac { zeta + { bar { zeta}}} { zeta { bar { zeta}} + 1}} x_ { 2} & = { frac { zeta - { bar { zeta}}} {i ( zeta { bar { zeta}} + 1)}} x_ {3} & = { frac { zeta { bar { zeta}} - 1} { zeta { bar { zeta}} + 1}}. end {выравнивается}}}$

(4)

Действие SO⁺(1,3) на точках N⁺ не сохраняет гиперплоскость S⁺, но действуя по точкам в S⁺ а затем масштабирование, чтобы результат снова был в S⁺ дает действие SO⁺(1,3) на сфере, которая переходит в действие на комплексную переменную ζ. Фактически, это действие осуществляется посредством дробно-линейных преобразований, хотя это нелегко увидеть из этого представления небесной сферы. Наоборот, для любого дробно-линейного преобразования переменной ζ переходит в единственное преобразование Лоренца на N⁺, возможно, после подходящего (однозначно определенного) изменения масштаба.

Более инвариантное описание стереографической проекции, которое позволяет более отчетливо видеть действие, - это рассмотрение переменной ζ =z:ш как отношение пары однородных координат комплексной проективной прямой CP¹. Стереографическая проекция переходит в преобразование из C² - {0} в N⁺ который однороден степени два относительно вещественных вычислений

${ displaystyle (z, w) mapsto (x_ {0}, x_ {1}, x_ {2}, x_ {3}) = (z { bar {z}} + w { bar {w}}) , z { bar {z}} - w { bar {w}}, z { bar {w}} + w { bar {z}}, i ^ {- 1} (z { bar {w }} - w { bar {z}}))}$

(5)

что согласуется с (4) при ограничении масштабами, в которых ${ displaystyle z { bar {z}} + w { bar {w}} = 1.}$ Компоненты (5) - это именно те, которые получены из внешнего продукта

${ displaystyle { begin {bmatrix} x_ {0} + x_ {1} & x_ {2} + ix_ {3} x_ {2} -ix_ {3} & x_ {0} -x_ {1} end { bmatrix}} = 2 { begin {bmatrix} z ​​ w end {bmatrix}} { begin {bmatrix} { bar {z}} & { bar {w}} end {bmatrix}}.}$

Таким образом, действие ограниченной группы Лоренца SO⁺(1,3) согласуется с таковой группы Мебиуса PSL (2,C). Это мотивирует следующее определение. В измерении п ≥ 2, Группа Мебиуса Möb (п) - группа всех сохраняющих ориентацию конформный изометрии круглой сферы S^п себе. Реализуя конформную сферу как пространство указывающих в будущее лучей нулевого конуса в пространстве Минковского р^{1, п + 1}, существует изоморфизм Möb (п) с ограниченной группой Лоренца SO⁺(1,п+1) преобразований Лоренца с положительным определителем, сохраняющих направление времени.

Вместо этого Кокстер начал с эквивалентной квадратичной формы ${ Displaystyle Q (x_ {1}, x_ {2}, x_ {3} x_ {4}) = x_ {1} ^ {2} + x_ {2} ^ {2} + x_ {3} ^ {2} -x_ {4} ^ {2}.}$

Он отождествил группу Лоренца с преобразованиями, для которых {Икс : Q (Икс) = -1} равно стабильный. Затем он интерпретировал x как однородные координаты и {Икс : Q (Икс) = 0}, нулевой конус, как Кейли абсолют для гиперболического пространства точек {Икс : Q (Икс) <0}. Затем Кокстер ввел переменные

${ displaystyle xi = { frac {x_ {1}} {x_ {4}}}, eta = { frac {x_ {2}} {x_ {4}}}, zeta = { гидроразрыв {x_ {3}} {x_ {4}}}}$

так что лоренц-инвариантная квадрика соответствует сфере ${ displaystyle xi ^ {2} + eta ^ {2} + zeta ^ {2} = 1.}$ Коксетер отмечает, что Феликс Кляйн также писал об этом соответствии, применяя стереографическую проекцию из (0, 0, 1) на комплексную плоскость ${ displaystyle z = { frac { xi + i eta} {1- zeta}}.}$Кокстер использовал тот факт, что круги инверсной плоскости представляют собой плоскости гиперболического пространства, а общая гомография - это результат инверсий в двух или четырех окружностях, соответствующих общему гиперболическому смещению, которое является продуктом инверсий в двух или четырех плоскостях.

Гиперболическое пространство

Как видно выше, группа Мебиуса PSL (2,C) действует на пространстве Минковского как группа тех изометрий, которые сохраняют начало координат, ориентацию пространства и направление времени. Ограничение до точек, где Q= 1 в положительном световом конусе, которые образуют модель гиперболическое 3-пространство ЧАС ³, мы видим, что группа Мёбиуса действует на ЧАС ³ как группу изометрий, сохраняющих ориентацию. Фактически, группа Мёбиуса равна группе сохраняющих ориентацию изометрий гиперболического 3-пространства.

Если мы используем Модель шара Пуанкаре, идентифицируя единичный шар в р³ с ЧАС ³, то мы можем думать о сфере Римана как о «конформной границе» ЧАС ³. Всякая сохраняющая ориентацию изометрия ЧАС ³ приводит к преобразованию Мёбиуса на сфере Римана и наоборот; это самое первое наблюдение, ведущее к AdS / CFT корреспонденция домыслы в физике.

Смотрите также

Примечания

Рекомендации

Специфический

Общий

дальнейшее чтение

• Лоусон, М. В. (1998). "Обратный моноид Мёбиуса". Журнал алгебры. 200 (2): 428. Дои:10.1006 / jabr.1997.7242.

внешняя ссылка

• «Квазиконформное отображение», Энциклопедия математики, EMS Press, 2001 [1994]
• Галерея конформных карт
• Вайсштейн, Эрик В. «Дробное линейное преобразование». MathWorld.