Линия румба - Rhumb line

Изображение локсодромии, или линии румба, спиралевидной по направлению к Северный полюс

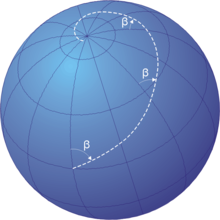
В навигация, а линия румба, румба, (/рʌм/) или же локсодромия дуга пересекает все меридианы из долгота под тем же углом, то есть путь с постоянным несущий как измерено относительно истинный или же магнитный север.

Вступление

Эффект от следования линии румба на поверхности земного шара впервые был обсужден португальский математик Педро Нунес в 1537 г., в его Трактат в защиту морской карты, с дальнейшим математическим развитием Томас Харриот в 1590-е гг.

Линию румба можно противопоставить большой круг, который представляет собой путь кратчайшего расстояния между двумя точками на поверхности сферы. На большом круге пеленг на пункт назначения не остается постоянным. Если бы кто-то вел машину по большому кругу, он бы удерживал рулевое колесо неподвижным, но чтобы следовать по прямой линии, нужно было бы повернуть колесо, поворачивая его более резко по мере приближения к полюсам. Другими словами, большой круг локально "прямой" с нулем геодезическая кривизна, тогда как прямая линия имеет ненулевую геодезическую кривизну.

Меридианы долготы и параллели широты представляют собой особые случаи прямой линии, где их углы пересечения составляют соответственно 0 ° и 90 °. На проходе с севера на юг курс румба совпадает с большим кругом, как и на проходе с востока на запад вдоль дороги. экватор.

На Проекция Меркатора карта, любая прямая линия является прямой линией; На такой карте можно провести прямую линию между любыми двумя точками на Земле, не выходя за край карты. Но теоретически локсодрома может выходить за правый край карты, где она затем продолжается у левого края с тем же наклоном (при условии, что карта покрывает ровно 360 градусов долготы).

Линии румба, которые пересекают меридианы под косыми углами, являются локсодромными кривыми, которые спиралевидно направляются к полюсам.^[1] В проекции Меркатора север и южные полюса происходят на бесконечности и поэтому никогда не отображаются. Однако полная локсодрома на бесконечно высокой карте будет состоять из бесконечно большого числа отрезков прямых между двумя краями. На стереографическая проекция карта, локсодрома - это равноугольная спираль чей центр - северный или южный полюс.

Все локсодромы по спирали из одного столб к другому. Рядом с полюсами они близки к логарифмические спирали (что они точно на стереографическая проекция см. ниже), поэтому они наматываются вокруг каждого полюса бесконечное число раз, но достигают полюса на конечном расстоянии. Межполюсная длина локсодрома (в предположении идеального сфера ) - длина меридиан разделенный на косинус пеленга от истинного севера. Локсодромы на полюсах не определяются.

Три вида межполюсной локсодромии

Этимология и историческое описание

Слово локсодромия происходит от Древнегреческий λοξός Loxós: "косой" + δρόμος Drómos: "бег" (от δραμεῖν драмен: "бежать"). Слово румба может прийти из испанский или же португальский румбо / румо ("курс" или "направление") и греческий ῥόμβος ромбо,^[2] из Рембейн.

Издание 1878 г. Энциклопедия всемирной информации Globe описывает линия локсодромии в качестве:^[3]

Локсодромный Линия - это кривая, которая разрезает каждый член системы линий кривизны данной поверхности под одним и тем же углом. Корабль, идущий к одной и той же точке компаса, описывает такую линию, которая пересекает все меридианы под одинаковым углом. В проекции Меркатора (см.) Локсодромические линии, очевидно, прямые.^[3]

Может возникнуть недопонимание, потому что термин «румб» не имел точного значения, когда он вошел в употребление. Он одинаково хорошо относился к линии розы ветров как это произошло с локсодромами, потому что этот термин применялся только «локально» и означал только то, что делал моряк, чтобы плавать с постоянным несущий, со всей возможной неточностью. Таким образом, «румба» применялась к прямым линиям на портоланы когда использовались портоланы, а также всегда применимо к прямым линиям на картах Меркатора. Для коротких расстояний «румбы» с пороланом существенно не отличаются от румбов Меркатора, но в наши дни «румб» является синонимом математически точного «локсодрома», потому что ретроспективно его сделали синонимом.

Как утверждает Лео Багроу:^[4] "... слово ('Rhumbline') неправильно применяется к морским картам этого периода, поскольку локсодромия дает точный курс только тогда, когда карта построена на подходящей проекции. Картометрическое исследование показало, что проекция не использовалась в ранние диаграммы, для которых мы поэтому сохраняем название «portolan» ».

Математическое описание

Для сферы радиуса 1 азимутальный и полярный углы $λ$ и $- π / 2 \leq φ \leq π / 2$ (определяется здесь, чтобы соответствовать широте) и Декартовы единичные векторы $я$ , $j$ , и $k$ можно использовать для записи радиус-вектора $р$ в качестве

{ displaystyle mathbf {r} ( lambda, varphi) = ( cos { lambda} cdot cos { varphi}) mathbf {i} + ( sin { lambda} cdot cos { varphi}) mathbf {j} + ( sin { varphi}) mathbf {k} ,.}

Ортогональные единичные векторы в азимутальном и полярном направлениях сферы можно записать

{ displaystyle { begin {align} { boldsymbol { hat { lambda}}} ( lambda, varphi) & = sec { varphi} { frac { partial mathbf {r}} { partial lambda}} = (- sin { lambda}) mathbf {i} + ( cos { lambda}) mathbf {j} ,, [8pt] { boldsymbol { hat { varphi}}} ( lambda, varphi) & = { frac { partial mathbf {r}} { partial varphi}} = (- cos { lambda} cdot sin { varphi}) mathbf {i} + (- sin { lambda} cdot sin { varphi}) mathbf {j} + ( cos { varphi}) mathbf {k} ,, end {выровнено} }}

которые имеют скалярные произведения

{ displaystyle { boldsymbol { hat { lambda}}} cdot { boldsymbol { hat { varphi}}} = { boldsymbol { hat { lambda}}} cdot mathbf {r} = { boldsymbol { hat { varphi}}} cdot mathbf {r} = 0 ,.}

$λ̂$ для постоянного $φ$ проводит параллель по широте, а $φ̂$ для постоянного $λ$ определяет меридиан долготы, и вместе они образуют плоскость, касательную к сфере.

Единичный вектор

{ displaystyle mathbf { boldsymbol { hat { beta}}} ( lambda, varphi) = ( sin { beta}) { boldsymbol { hat { lambda}}} + ( cos { beta}) { boldsymbol { hat { varphi}}}}}

имеет постоянный угол $β$ с единичным вектором $φ̂$ для любого $λ$ и $φ$ , поскольку их скалярное произведение равно

{ displaystyle { boldsymbol { hat { beta}}} cdot { boldsymbol { hat { varphi}}} = cos { beta} ,.}

Локсодрома определяется как кривая на сфере, имеющая постоянный угол $β$ со всеми меридианами долготы и, следовательно, должны быть параллельны единичному вектору $β̂$ . В результате разница в длине $ds$ вдоль локсодрома будет производить дифференциальное смещение

{ displaystyle { begin {align} d mathbf {r} & = { boldsymbol { hat { beta}}} , ds [8px] { frac { partial mathbf {r}} { partial lambda}} , d lambda + { frac { partial mathbf {r}} { partial varphi}} , d varphi & = (( sin { beta}) , { boldsymbol { hat { lambda}}} + ( cos { beta}) , { boldsymbol { hat { varphi}}}) ds [8px] ( cos { varphi}) , d lambda , { boldsymbol { hat { lambda}}} + d varphi , { boldsymbol { hat { varphi}}} & = ( sin { beta}) , ds , { boldsymbol { hat { lambda}}} + ( cos { beta}) , ds , { boldsymbol { hat { varphi}}} [8px] ds & = { frac { cos { varphi}} { sin { beta}}} , d lambda = { frac {d varphi} { cos { beta}}} [8px] { frac {d lambda} {d varphi}} & = tan { beta} cdot sec { varphi} [8px] lambda ( varphi , | , beta, lambda _ {0}, varphi _ {0}) & = tan beta cdot { big (} operatorname {artanh} ( sin varphi) - operatorname {artanh} ( sin varphi _ {0}) { big) } + lambda _ {0} [8px] varphi ( lambda , | , beta, lambda _ {0}, varphi _ {0}) & = arcsin { Big (} tanh { big (} ( lambda - lamb da _ {0}) cot beta + operatorname {artanh} ( sin varphi _ {0}) { big)} { Big)} end {align}}}

С этой связью между $λ$ и $φ$ , радиус-вектор становится параметрической функцией одной переменной, отслеживая локсодрому на сфере:

{ displaystyle mathbf {r} ( lambda , | , beta, lambda _ {0}, varphi _ {0}) = { Big (} cos { lambda} cdot operatorname { sech} psi { Big)} mathbf {i} + { Big (} sin { lambda} cdot operatorname {sech} psi { Big)} mathbf {j} + { Big ( } tanh psi { Big)} mathbf {k} ,,}

куда

{ Displaystyle psi Equiv ( lambda - lambda _ {0}) cot beta + operatorname {artanh} ( sin varphi _ {0}) = operatorname {artanh} ( sin varphi) }

это изометрическая широта.^[5] Геоцентрический и изометрические широты связаны друг с другом через Функция Гудермана,

{ displaystyle varphi = operatorname {gd} ( psi) ,.}

По линии Румба, когда геоцентрическая широта стремится к полюсам, $φ \to \pm π / 2$ , $грех φ \to \pm1$ , изометрическая широта $артанх (грех φ) \to \pm \infty$ , и долгота $λ$ неограниченно возрастает, очень быстро вращая сферу по спирали к полюсу, стремясь к конечной общей длине дуги Δ $s$ данный

{ displaystyle Delta s = { big |} ( pm pi / 2- varphi _ {0}) cdot sec beta { big |}}

Подключение к проекции Меркатора

Позволять $λ$ - долгота точки на сфере, а $φ$ его широта. Тогда, если мы определим координаты карты Проекция Меркатора в качестве

{ displaystyle { begin {align} x & = lambda - lambda _ {0} ,, y & = operatorname {arctanh} ( sin varphi) ,, end {выровнено}}}

локсодромия с постоянным несущий $β$ от истинного севера будет прямая линия, поскольку (используя выражение в предыдущем разделе)

{ displaystyle y = mx}

с уклоном

{ Displaystyle м = детская кроватка бета ,.}

Нахождение локсодромов между двумя заданными точками может быть выполнено графически на карте Меркатора или путем решения нелинейной системы двух уравнений относительно двух неизвестных. $м = детская кроватка β$ и $λ 0$ . Есть бесконечно много решений; самый короткий - тот, который покрывает фактическую разницу долготы, то есть не делает лишних оборотов и не идет «в обратном направлении».

Расстояние между двумя точками Δ $s$ , измеренная вдоль локсодромии, представляет собой просто абсолютное значение секущий пеленга (азимута), умноженного на расстояние с севера на юг (за исключением круги широты для которого расстояние становится бесконечным):

{ Displaystyle Delta s = R , { big |} ( varphi - varphi _ {0}) cdot sec beta { big |}}

куда $р$ один из средние радиусы Земли.

Заявление

Его использование в навигации напрямую связано со стилем, или проекция некоторых навигационных карт. Линия румба выглядит как прямая линия на Проекция Меркатора карта.^[1]

Название происходит от старофранцузского или испанского соответственно: "румба" или «румбо», линия на графике, пересекающая все меридианы под одним углом.^[1] На плоской поверхности это будет кратчайшее расстояние между двумя точками. Над поверхностью Земли на низких широтах или на коротких расстояниях его можно использовать для прокладки курса транспортного средства, самолета или корабля.^[1] На больших расстояниях и / или в более высоких широтах большой круг маршрут значительно короче, чем прямая линия между теми же двумя точками. Однако неудобство от необходимости постоянно менять пеленг во время движения по маршруту большого круга делает румбовая линия навигации привлекательные в определенных случаях.^[1]

Это можно проиллюстрировать переходом с востока на запад на 90 градусов долготы вдоль экватор, для которого расстояния по большому кругу и прямой линии равны 5 400 морских миль (10 000 км). На 20 градусах северной широты расстояние по большому кругу составляет 4 997 миль (8 042 км), а расстояние по прямой линии составляет 5 074 мили (8 166 км), т.е.1 ¹⁄₂ процентов дальше. Но на 60 градусах северной широты расстояние по большому кругу составляет 2485 миль (3999 км), а прямая линия - 2700 миль (4300 км), то есть разница составляет8 ¹⁄₂ процентов. Более крайний случай - воздушный маршрут между Нью-Йорк и Гонконг, для которой путь прямой линии составляет 9 700 морских миль (18 000 км). Маршрут большого круга над Северным полюсом составляет 7000 морских миль (13000 км), или5 ¹⁄₂ часов меньше летного времени при типичном крейсерская скорость.

Некоторые старые карты в проекции Меркатора имеют сетки, состоящие из линий широта и долгота но также показывают линии румба, которые ориентированы прямо на север, под прямым углом с севера или под некоторым углом с севера, который представляет собой простую рациональную часть прямого угла. Эти линии румба будут нарисованы так, чтобы они сходились в определенных точках карты: линии, идущие во всех направлениях, сходились бы в каждой из этих точек. Видеть картушка. Такие карты обязательно должны были быть в проекции Меркатора, поэтому не все старые карты были способны показать разметку прямой линии.

Радиальные линии на розете ветров еще называют румянец. Выражение "плыть по румбу" использовался в XVI – XIX веках для обозначения определенного направления по компасу.^[1]

Ранние мореплаватели еще до изобретения морской хронометр использовали курсы румба на длинных океанских переходах, потому что широту корабля можно было точно установить по наблюдениям Солнца или звезд, но не было точного способа определения долготы. Корабль будет плыть на север или юг, пока не будет достигнута широта пункта назначения, а затем корабль будет плыть на восток или запад по прямой линии (фактически параллельно, который является частным случаем прямой линии), поддерживая постоянную широту и записывая регулярные оценки пройденного расстояния до тех пор, пока не будут обнаружены признаки земли.^[6]

Обобщения

О сфере Римана

Математически поверхность Земли можно понять как Сфера Римана, то есть как проекция сферы на комплексная плоскость. В этом случае под локсодромами можно понимать определенные классы Преобразования Мебиуса.

Сфероид

Приведенная выше формулировка может быть легко расширена до сфероид.^[7]^[8]^[9]^[10]^[11] Линия румба определяется просто с помощью эллипсоидального изометрическая широта. Аналогичным образом расстояния находятся путем умножения эллипсоидальных дуга меридиана длина по секущей азимута.

Смотрите также

дальнейшее чтение

Монмонье, Марк (2004). Линии румба и карты войн. Социальная история проекции Меркатора. Чикаго: Издательство Чикагского университета. ISBN 9780226534329.

внешняя ссылка

Постоянные заголовки и строки румба на MathPages.
RhumbSolve (1), утилита для расчета эллипсоидальных линий румба (компонент GeographicLib ); дополнительная документация.
Онлайн-версия RhumbSolve.
Навигационные алгоритмы Бумага: Парусный спорт.
Работа с картами - навигационные алгоритмы Бесплатное программное обеспечение для работы с картами: Rhumb line, Great Circle, Composite sailing, Meridional parts. Линии позиции «Пилотирование» - течения и береговая привязка.
Mathworld Локсодромия.

[EOS-1] а ^б ^c ^d ^е ^ж Oxford University Press Rhumb Line. Oxford Companion to Ships and the Sea, Oxford University Press, 2006. Получено с Encyclopedia.com 18 июля 2009 г.

[2] Румб в TheFreeDictionary

[Globe-3] а ^б Росс, J.M. (редактор) (1878). Энциклопедия всемирной информации Globe, Vol. IV, Эдинбург, Шотландия, Томас К. Джек, Grange Publishing Works, взято из Google Книги 2009-03-18;

[Bagrow2010-4] Лео Багроу (2010). История картографии. Издатели транзакций. п. 65. ISBN 978-1-4128-2518-4.

[5] Джеймс Александер, Локсодромы: глупый путь, "Mathematics Magazine", Vol. 77. № 5, декабрь 2004 г. [1]

[6] Краткая история британской морской мощи, Дэвид Ховарт, паб. Констебль и Робинсон, Лондон, 2003 г., глава 8.

[7] Смарт, У. М. (1946). «О проблеме в навигации». Ежемесячные уведомления Королевского астрономического общества. 106 (2): 124–127. Bibcode:1946МНРАС.106..124С. Дои:10.1093 / mnras / 106.2.124.CS1 maint: ref = harv (связь)

[8] Уильямс, Дж. Э. Д. (1950). «Локсодромные расстояния на земном сфероиде». Журнал навигации. 3 (2): 133–140. Дои:10.1017 / S0373463300045549.CS1 maint: ref = harv (связь)

[9] Карлтон-Випперн, К. С. (1992). «О локсодромной навигации». Журнал навигации. 45 (2): 292–297. Дои:10.1017 / S0373463300010791.CS1 maint: ref = harv (связь)

[10] Беннет, Г. Г. (1996). "Практические расчеты румба на сфероиде". Журнал навигации. 49 (1): 112–119. Bibcode:1996JNav ... 49..112B. Дои:10.1017 / S0373463300013151.CS1 maint: ref = harv (связь)

[11] Ботнев, В. А; Устинов, С. (2014). Методы решения прямых и обратных геодезических задач с высокой точностью [Методы решения прямых и обратных геодезических задач с высокой точностью] (PDF). Вестник Санкт-Петербургского государственного политехнического университета (на русском). 3 (198): 49–58.CS1 maint: ref = harv (связь)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]