Геодезические на эллипсоиде - Geodesics on an ellipsoid
| Геодезия | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||||||||||||||||
Концепции
| ||||||||||||||||||||||||||
Стандарты (история)
| ||||||||||||||||||||||||||

Изучение геодезические на эллипсоиде возник в связи с геодезия конкретно с решением сети триангуляции. Вфигура Земли хорошо аппроксимируетсясплюснутый эллипсоид, слегка приплюснутый шар. А геодезический - кратчайший путь между двумя точками на искривленной поверхности, аналогичный прямая линия на ровной поверхности. Решение триангуляционной сети на эллипсоиде представляет собой комплекс упражнений по сфероидальтригонометрии (Эйлер 1755 ).
Если рассматривать Землю как сфера, геодезическиебольшие круги (все они закрыты), и проблемы сводятся к сферическая тригонометрия. Тем не мение, Ньютон (1687) показали, что эффект вращения Земли приводит к тому, что она напоминает слегка сплющенный эллипсоид: в этом случаеэкватор и меридианы являются единственными простыми замкнутыми геодезическими. Более того, кратчайший путь между двумя точками на экваторе не обязательно проходит вдоль экватора. Наконец, если эллипсоид подвергнется дальнейшему возмущению и станет трехосный эллипсоид (с тремя различными полуосями) замкнуты только три геодезические.
Геодезические на эллипсоиде вращения
Есть несколько способов определения геодезических (Гильберт и Кон-Фоссен, 1952 г. С. 220–221). Простое определение - это кратчайший путь между двумя точками на поверхности. Однако часто бывает полезнее определять их как пути с нулевымгеодезическая кривизна - т.е. аналог прямые линии на изогнутой поверхности. Это определение охватывает геодезические, перемещающиеся так далеко по поверхности эллипсоида, что они начинают возвращаться к начальной точке, так что другие маршруты являются более прямыми и включают пути, которые пересекаются или пересекаются заново. Достаточно короткие сегменты геодезических по-прежнему являются кратчайшим путем между их конечными точками, но геодезические не обязательно являются глобально минимальными (то есть самыми короткими среди всех возможных путей). Каждый кратчайший в мире путь является геодезическим, но не наоборот.
К концу XVIII века эллипсоид вращения (терминсфероид также используется) было общепринятым приближением кфигура Земли. Регулировка сети триангуляции повлекло за собой сокращение всех измерений до опорный эллипсоид и решение полученной двумерной задачи в виде упражнения на героидальную тригонометрию (Бомфорд 1952, Гл. 3) (Leick et al. 2015 г., §4.5).

Можно свести различные геодезические задачи к одному из двух типов. Учтите два момента: А в широтаφ1 и долгота λ1 иB на широте φ2 и долготаλ2 (см. рис. 1). Соединительная геодезическая (от А к B) является AB, длиныs12, у которого есть азимуты α1 иα2 на двух конечных точках.[1] Обычно рассматриваются две геодезические задачи:
- то прямая геодезическая задача или же первая геодезическая задача, данный А, α1, и s12, определять B и α2;
- то обратная геодезическая задача или же вторая геодезическая задача, данный А и B, определять s12, α1, и α2.
Как видно из рис.1, эти задачи связаны с решением треугольникаNAB учитывая один угол, α1 для прямой задачи и λ12 = λ2 - λ1 для обратной задачи и двух ее смежных сторон. для сферы решения этих задач представляют собой простые упражнения всферическая тригонометрия, решение которой дается формулойформулы решения сферического треугольника. (См. Статью о круговая навигация.)
Для эллипсоида вращения характеристическая постоянная, определяющая геодезические свойства, была найдена следующим образом: Клеро (1735). Систематическое решение для путей геодезических далЛежандр (1806) иОриани (1806) (и последующие статьи в1808 и1810 Полное решение прямой задачи (с расчетными таблицами и разработанным примером) дает Бессель (1825).
В течение 18 века геодезические обычно назывались «кратчайшими линиями». Термин «геодезическая линия» был введен в обращение Лаплас (1799b):
Nous désignerons cette ligne sous le nom de Ligne Géodésique [Мы будем называть эту линию геодезическая линия].
Эта терминология была введена в английский язык как «геодезическая линия» или как «геодезическая линия», например (Хаттон 1811 ),
Линия, проведенная так, как мы сейчас описываем, или выведенная из тригонометрических мер указанными нами средствами, называется геодезический или же геодезическая линия: он имеет свойство быть самым коротким, который может быть проведен между двумя его краями на поверхности Земли; и поэтому это правильная маршрутная мера расстояния между этими двумя точками.
В его принятии в других областях геодезическая линия, часто сокращается до геодезический, было предпочтительнее.
В этом разделе рассматривается задача об эллипсоиде вращения (двухугольном и вытянутом). Задача о трехосном эллипсоиде рассматривается в следующем разделе.
Уравнения геодезической


Здесь разрабатываются уравнения геодезической; вывод близко следует за выводом Бессель (1825).Джордан и Эггерт (1941),Багратуни (1962 г., §15),Ганьшин (1967 г., Гл. 5),Краковский и Томсон (1974), §4),Рэпп (1993, §1.2),Джекели (2012), иБорре и Стрэнг (2012) также приведем вывод этих уравнений.
Рассмотрим эллипсоид вращения с экваториальным радиусома и полярная полуось б. Определить сглаживание ж = (а − б)/а, эксцентриситете = √а2 − б2/а = √ж(2 − ж), а вторая децентриситет е′ = √а2 − б2/б = е/(1 − ж). (В большинстве случаев в геодезии эллипсоид считается сжатым,а > б; однако теория без изменений применима к вытянутым эллипсоидам, а < б, в таком случае ж, е2, и е′2 отрицательны.)
Пусть элементарный отрезок пути на эллипсоиде имеет длинуds. Из фиг. 2 и 3, мы видим, что если его азимут равен α, тогда dsотносится к dφ и dλ к
- (1)
куда ρ этомеридиональный радиус кривизны,р = ν cosφ это радиус круга широтыφ, и ν этонормальный радиус кривизны Таким образом, элементарный сегмент имеет вид
или же
куда φ ′ = dφ /dλ иФункция Лагранжа L зависит отφ через р (ф) ир(φ). Длина произвольного пути между(φ1, λ1) и (φ2, λ2) дан кем-то
куда φ является функцией λ удовлетворениеφ (λ1) = φ1 иφ (λ2) = φ2. Кратчайший путь или геодезический не позволяет найти эту функцию φ (λ) что сводит к минимумуs12. Это упражнение ввариационное исчисление а условие минимизации задаетсяБелтрами личность,
Замена на L и используя уравнения. (1) дает
Клеро (1735) нашел это связь, используя геометрическую конструкцию; аналогичный вывод представленЛюстерник (1964 г., §10).[2] Дифференциация этой связи дает
Это вместе с уравнениями. (1), приводит к системеобыкновенные дифференциальные уравнения для геодезической
Мы можем выразить р с точки зренияпараметрическая широта,β,с помощью
и отношение Клеро становится


Это правило синуса сферической тригонометрии, связывающей две стороны треугольника NAB (см. рис. 4), NA = 1⁄2π - β1, иNB = 1⁄2π - β2 и их противоположные углыB = π - α2 и А = α1.
Чтобы найти соотношение для третьей стороныAB = σ12, то длина сферической дуги, и включенный угол N = ω12, то сферическая долгота, полезно рассмотреть треугольник Нэп представляющий геодезический старт на экваторе; см. рис. 5. На этом рисунке переменные, относящиеся к вспомогательной сфере, показаны с соответствующими величинами для эллипсоида, показанными в скобках. Величины без индексов относятся к произвольной точкеп; E, точка, в которой геодезическая пересекает экватор в северном направлении, используется как начало координат дляσ, s и ω.
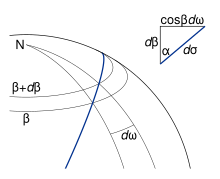
Если сторона EP расширяется путем перемещения п бесконечно малой (см. рис. 6) получаем
- (2)
Комбинируя уравнения. (1) и (2) дают дифференциальные уравнения для s и λ
Связь между β и φ является
который дает
так что дифференциальные уравнения для геодезической становятся
Последний шаг - использовать σ как независимый параметр в обоих этих дифференциальных уравнениях и тем самым выражать s иλ в виде интегралов. Применение правила синуса к вершинамE и грамм в сферическом треугольникеEGP на рис.5 дает
куда α0 азимут в E.Подставляя это в уравнение для ds/dσ и интеграция результата дает
- (3)
куда
а пределы интеграла выбраны так, чтобыs(σ = 0) = 0. Лежандр (1811 г., п. 180) указал, что уравнение для s совпадает с уравнением длядуга на эллипсе с полуосями б√1 + е′2 потому что2α0 иб. Чтобы выразить уравнение дляλ с точки зрения σ, мы пишем
что следует из уравнения. (2) и соотношение Клеро, что дает
- (4)
а пределы интегралов выбраны так, чтобы λ = λ0 на пересечении экватора,σ = 0.
На этом решение пути геодезической с использованием вспомогательной сферы завершено. С помощью этого устройства можно точно сопоставить большой круг с геодезической на эллипсоиде вращения.
Также существует несколько способов аппроксимации геодезических на земном эллипсоиде (с небольшим уплощением) (Рэпп 1991, §6); некоторые из них описаны в статье о географическое расстояние Однако они обычно сравнимы по сложности с методом точного решения (Jekeli 2012, §2.1.4).
Поведение геодезических



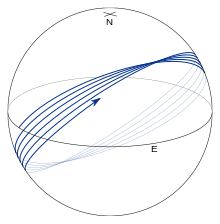
На рис. 7 показаны простые замкнутые геодезические, состоящие из тридианов (зеленый) и экватора (красный). (Здесь определение «простой» означает, что геодезическая замыкается на себя без промежуточного самопересечения.) Это следует из уравнений для геодезических, приведенных в предыдущем разделе.
Все остальные геодезические представлены на рис. 8 и 9, на которых показана геодезическая, начинающаяся на экваторе сα0 = 45°. Геодезическая колеблется вокруг экватора. Экваториальные пересечения называются узлы а точки максимальной или минимальной широты называются вершины; параметрические широты вершин равныβ = ± (1⁄2π - | α0|)Геодезическая совершает одно полное колебание по широте, прежде чем долгота увеличится на 360°Таким образом, при каждом последующем пересечении экватора на север (см. Рис. 8) λ не доходит до полного оборота экватора примерно на 2π ж sinα0 (для апролатного эллипсоида эта величина отрицательна и λсовершает больше, чем полный цикл; см. рис.10). Почти для всех значений α0, геодезическая заполнит ту часть эллипсоида между двумя широтами вершин (см. рис. 9).


Если эллипсоид достаточно сплюснутый, т. Е.б⁄а < 1⁄2возможен другой класс простых замкнутых геодезических (Клингенберг 1982, §3.5.19). Две такие геодезические показаны на рис. 11 и 12. Здесьб⁄а = 2⁄7 и экваториальный азимут,α0, поскольку зеленая (соответственно синяя) геодезическая выбрана 53.175° (соотв. 75.192°), так что геодезическая совершает 2 (соответственно 3) полных колебания вокруг экватора на одном витке эллипсоида.

На Рис.13 показаны геодезические (синим цветом), исходящиеА с α1 кратный15° вплоть до того момента, когда они перестают быть кратчайшими путями. (Сглаживание увеличено до1⁄10 чтобы подчеркнуть эллипсоидальные эффекты.) Также показаны (зеленым цветом) кривые постоянной s12, которые представляют собой геодезические окружности с центром А.Гаусс (1828) показал, что на любой поверхности геодезические и геодезическая окружность пересекаются под прямым углом. Красная линия - этовырезать место, геометрическое место точек, которые имеют кратчайшие (в данном случае две) кратчайшие геодезические из А. На сфере разрез - это точка. На сплющенном эллипсоиде (показанном здесь) это сегмент круга широты с центром в точке противоположный к А, φ = −φ1. Продольная протяженность локуса разреза составляет приблизительноλ12 ∈ [π - ж π cosφ1, π + ж π cosφ1]. ЕслиА лежит на экваторе, φ1 = 0, это соотношение является точным, и, как следствие, экватор является кратчайшей геодезической, только если| λ12| ≤ (1 − ж) π. Для вытянутого эллипсоида место разреза - это сегмент антимеридиана с центром в точке, противоположной точке. А, λ12 = π, а это означает, что меридиональные геодезические перестают быть кратчайшими путями до того, как будет достигнута точка противоположности.
Дифференциальные свойства геодезических
Различные проблемы, связанные с геодезическими, требуют знания их поведения при возмущении. Это полезно при тригонометрической настройке (Ehlert 1993 ), определяющие физические свойства сигналов, следующих за геодезическими, и т. д. Рассмотрим опорную геодезическую, параметризованную s, а вторая геодезическая - на небольшом расстоянии т(s) подальше от него. Гаусс (1828) показало, чтот(s) подчиняетсяУравнение Гаусса-Якоби

куда K(s) это Гауссова кривизна в sКак линейное однородное дифференциальное уравнение второго порядка, его решение может быть выражено как сумма двух независимых решений.
куда
Количество м(s1, s2) = м12 так называемыйуменьшенная длина, и M(s1, s2) = M12 этогеодезическая шкала.[3]Их основные определения проиллюстрированы на рис. 14.
ВГауссова кривизна эллипсоида вращения является
Гельмерт (1880 г., Уравнение (6.5.1.)) Решил уравнение Гаусса-Якоби для этого случая, разрешив м12 иM12 выражаться в виде интегралов.
Как видно из рис. 14 (верхний подрисунок), разделение двух геодезических, начинающихся в одной точке с азимутами, различающимися наdα1 является м12 dα1. На замкнутой поверхности, например эллипсоиде, м12 колеблется около нуля. Точка, в которой м12 становится нулем это точкасопрягать к исходной точке. Для геодезической между А и B, длиныs12, чтобы быть кратчайшим, он должен удовлетворять условию Якоби (Якоби 1837 ) (Якоби 1866, §6)(Форсайт 1927, §§26–27)(Блаженство 1916 ), что нет точки, сопряженной А между А иB. Если это условие не выполняется, то существуетрядом путь (не обязательно геодезический), который короче. Таким образом, условие Якоби является локальным свойством геодезической и является лишь необходимым условием того, что геодезическая является кратчайшим глобальным путем. Необходимые и достаточные условия для того, чтобы геодезическая была кратчайшим путем, следующие:
- для сплющенного эллипсоида, | σ12| ≤ π;
- для вытянутого эллипсоида, | λ12| ≤ π, если α0 ≠ 0; если α0 = 0, дополнительное условие м12 ≥ 0 требуется, если | λ12| = π.
Конверт геодезических
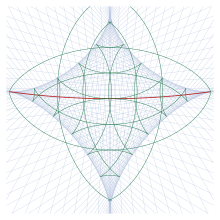

Геодезические из определенной точки А если продолжить мимо, геометрическое место разреза образует конверт, показанный на рис. 15, здесь геодезические, для которых α1 кратно3° показаны голубым цветом. (Геодезические показаны только для их первого прохождения близко к противоположной точке, но не для последующих.) Некоторые геодезические круги показаны зеленым; эти формы на конверте. Место разреза показано красным. Огибающая - это геометрическое место точек, сопряженных с А; точки на конверте можно вычислить, найдя точку, в которойм12 = 0 по геодезической.Якоби (1891) называет эту звездную фигуру, созданную конвертом, астроид.
Вне астроиды в каждой точке пересекаются две геодезические; таким образом, есть две геодезические (длиной примерно половину окружности эллипсоида) между А и эти точки. Это соответствует ситуации на сфере, где есть «короткий» и «длинный» маршруты на большом круге между двумя точками. Внутри астроида в каждой точке пересекаются четыре геодезические. Четыре таких геодезических показаны на рис. 16, где геодезические пронумерованы в порядке увеличения длины. (На этом рисунке используется та же позиция дляА как на рис.13 и нарисована в той же проекции.) Две более короткие геодезические стабильный, т.е. м12 > 0, так что не существует ближайшего пути, соединяющего две точки, который является более коротким; два других нестабильны. Только самая короткая линия (первая) имеет σ12 ≤ π. Все геодезические касаются оболочки, которая показана на рисунке зеленым цветом.
Астроид (внешний) эволюционировать геодезических окружностей с центром в А. Точно так же геодезические кругиэвольвенты астроиды.
Площадь геодезического многоугольника
А геодезический многоугольник - многоугольник, стороны которого являются геодезическими. Это аналог сферический многоугольник, стороны которого представляют собой большие круги. Площадь такого многоугольника можно найти, сначала вычислив площадь между агеодезическим сегментом и экватором, то есть площадь четырехугольника.AFHB на рис.1 (Даниэльсен 1989 ). Как только эта площадь известна, площадь многоугольника может быть вычислена путем суммирования вкладов от всех краев многоугольника.
Здесь выражение для площади S12 из AFHBразработан после Сьёберг (2006). Площадь любой замкнутой области эллипсоида равна
куда dT является элементом площади поверхности и Kэто Гауссова кривизна. ТеперьТеорема Гаусса – Бонне применяется к состояниям геодезического многоугольника
куда
- геодезический эксцесс и θj внешний угол при вершине j. Умножая уравнение на Γк р22, куда р2 этоаутентичный радиус, и вычитая это из уравнения для Т дает
где значение K для эллипсоида был заменен. Применяя эту формулу к четырехугольнику AFHB, отмечая, что Γ = α2 - α1, а интеграл по φ дает
где интеграл ведется по геодезической (так что φнеявно является функцией λИнтеграл можно представить в виде ряда, справедливого при малых ж(Даниэльсен 1989 ) (Карни 2013, §6 и приложение).
Площадь геодезического многоугольника определяется суммированием S12по его краям. Этот результат верен при условии, что многоугольник не включает полюс; если это так, 2π р22 необходимо добавить к сумме. Если ребра задаются своими вершинами, тоудобное выражение за геодезический избыток E12 = α2 - α1 является
Решение прямой и обратной задач.
Решение геодезических задач влечет за собой отображение геодезической на вспомогательную сферу и решение соответствующей задачи вкруговая навигация.При решении «простейшего» сферического треугольника для Нэп на рис.5,Правила Напье для квадрантных треугольников можно использовать,
Отображение геодезической включает в себя оценку интегралов для расстояния, s, и долгота,λ, Уравнения. (3) и (4) и зависят от параметра α0.
Решение прямой проблемы несложно, потому чтоα0 можно определить непосредственно из заданных величин φ1 и α1.
В случае обратной задачи λ12 дается; это не может быть легко связано с эквивалентным сферическим угломω12 потому что α0 неизвестно, поэтому для решения проблемы необходимо, чтобы α0 находить итеративно.
В геодезических приложениях, где ж мала, интегралы обычно вычисляются как ряд (Legendre 1806 г. )(Ориани 1806 ) (Бессель 1825 ) (Гельмерт 1880 г. )(Рейнсфорд 1955 ) (Рэпп 1993 ). Для произвольныхж, интегралы (3) и (4) могут быть найдены с помощью числовой квадратуры или выражением их черезэллиптические интегралы (Legendre 1806 г. ) (Кэли 1870 ).
Винсенти (1975) предоставляет решения для прямых и обратных задач; они основаны на последовательном расширении, выполняемом до третьего порядка при выравнивании, и обеспечивают точность около0,1 мм для WGS84 эллипсоид; однако обратный метод не может сходиться почти для противоположных точек. Карни (2013) продолжает расширения до шестого порядка, которого достаточно для обеспечения полногодвойная точность точность для|ж| ≤ 1⁄50 и улучшает решение обратной задачи так, чтобы оно сходилось во всех случаях.Карни (2013), добавление) расширяет метод за счет использования эллиптических интегралов, которые можно применять к эллипсоидам с произвольным уплощением.
Геодезические на трехосном эллипсоиде
Решение геодезической задачи для эллипсоида вращения с математической точки зрения относительно просто: из-за симметрии геодезические имеют постоянная движения, данное Клеро отношением, позволяющим свести проблему кквадратура. К началу 19 века (по творчеству Лежандра, Ориани, Бессель и др.), Было полное понимание свойств геодезических на анеллипсоиде вращения.
С другой стороны, геодезические на трехосном эллипсоиде (с тремя неравными осями) не имеют очевидной постоянной движения и, таким образом, представляли собой сложную нерешенную проблему в первой половине XIX века. В замечательной статье Якоби (1839) обнаружил постоянную движения, позволившую свести эту задачу также к квадратуре (Клингенберг 1982, §3.5).[4]
Трехосная система координат
Рассмотрим эллипсоид, определяемый формулой
куда (Икс,Y,Z) являются декартовыми координатами с центром на эллипсоиде и, без ограничения общности,а ≥ б ≥ c > 0.[5]Якоби (1866 г., §§26–27) использовали эллипсоидальный широта и долгота(β, ω) определяется

В пределе б → а, βстановится параметрической широтой для сжатого эллипсоида, поэтому использование символа β согласуется с предыдущими разделами. ω является разные от сферической долготы, определенной выше.[6]
Линии сетки постоянных β (синим цветом) иω (зеленым цветом) представлены на рис. 17. Они представляют собой ортогональный система координат: линии сетки пересекаются под прямым углом. Основные секции эллипсоида, определяемые Икс = 0 и Z = 0 показаны красным цветом. Третий основной раздел, Y = 0, покрывается линиями β = ± 90 ° и ω = 0 ° или же±180°. Эти строки встречаются в четырепупочные точки (два из которых видны на этом рисунке), гдеглавные радиусы кривизны равны. Здесь и на других рисунках в этом разделе параметры эллипсоида а:б:c = 1.01:1:0.8, и он рассматривается в ортогональной проекции с точки выше φ = 40 °,λ = 30 °.
Линии сетки эллипсоидальных координат можно интерпретировать тремя различными способами:
- Это «линии кривизны» на эллипсоиде: они параллельны направлениям главной кривизны (Монж 1796 ).
- Они также являются пересечениями эллипсоида с конфокальные системы гиперболоидов одного и двух листов (Дюпен 1813, Часть 5 ).
- Наконец, они являются геодезическими эллипсами и гиперболами, определенными с помощью двух смежных омбилических точек (Гильберт и Кон-Фоссен, 1952 г., п. 188). Например, линии постоянного β на рис. 17 можно сгенерировать знакомым струнная конструкция для эллипсов концы веревки прикреплены к двум точкам пуповины.
Решение Якоби
Якоби показал, что уравнения геодезических, выраженные в эллипсоидальных координатах, разделимы. Вот как он рассказал о своем открытии своему другу и соседу Бесселю (Якоби 1839, Письмо Бесселю),
Позавчера я свел к квадратуре задачу о геодезических линиях на эллипсоид с тремя неравными осями. Это самые простые формулы в мире, Абелевы интегралы, которые становятся хорошо известными эллиптическими интегралами, если две оси равны.
Кенигсберг, 28 декабря '38.
Решение, данное Якоби (Якоби 1839 )(Якоби 1866, §28) является
Как отмечает Якоби, «функция угла β равняется функции угла ω. Эти две функции - всего лишь абелевы интегралы ... »Две константы δ иγ появляются в растворе. Обычноδ равен нулю, если нижние пределы интегралов принимаются за начальную точку геодезической, а направление геодезических определяется γ. Однако для геодезических, которые начинаются в точках пуповины, мы имеем γ = 0 иδ определяет направление в точке шлангокабеля. постоянная γ может быть выражено как
куда α - угол между геодезической и линиями постоянной ω. В пределе б → а, это сводится к sinα cosβ = const., знакомое соотношение Клеро. Вывод результата Якоби дается Дарбу (1894 г., §§583–584); Он дает решение, найденное Лиувиль (1846 г.) для общих квадратичных поверхностей.
Съемка трехосных геодезических


На трехосном эллипсоиде есть только три простых замкнутых геодезических, три главных сечения эллипсоида, заданных формулой Икс = 0,Y = 0, и Z = 0.[7]Для обзора других геодезических удобно рассматривать геодезические, которые пересекают средний главный участок, Y = 0, под прямыми углами. Такие геодезические показаны на рис. 18–22, которые используют те же параметры эллипсоида и то же направление обзора, что и на рис. 17. Кроме того, на каждом из этих рисунков красным цветом показаны три основных эллипса.
Если отправной точкой является β1 ∈ (−90°, 90°),ω1 = 0, и α1 = 90°, тогдаγ> 0 а геодезическая окружает эллипсоид в «циркумполярном» смысле. Геодезические колебания к северу и югу от экватора; при каждом колебании он совершает немного меньше, чем полный оборот вокруг эллипсоида, в результате чего в типичном случае геодезическая заполняет область, ограниченную двумя линиями широты. β = ± β1. Два примера приведены на рис. 18 и 19. На рис. 18 практически показано то же поведение, что и для сплющенного эллипсоида вращения (поскольку а ≈ б); сравните с рис.9. Однако, если начальная точка находится на более высокой широте (рис.18), искажения в результате а ≠ б очевидны. Все касательные к циркумполярной геодезической касаются конфокального однополостного гиперболоида, который пересекает эллипсоид в β = β1(Chasles 1846 г. )(Гильберт и Кон-Фоссен, 1952 г., стр. 223–224).


Если отправной точкой является β1 = 90°,ω1 ∈ (0°, 180°), иα1 = 180°, тогдаγ <0 а геодезическая окружает эллипсоид в «трансполярном» смысле. Геодезическая колеблется к востоку и западу от эллипса. Икс = 0; при каждом колебании он совершает немного больше, чем полный оборот вокруг эллипсоида. В типичном случае это приводит к тому, что геодезическая заполняет область, ограниченную двумя линиями долготы.ω = ω1 и ω = 180 ° - ω1.Если а = б, все меридианы геодезические; эффекта ≠ б заставляет такие геодезические колебаться на восток и запад. Два примера приведены на рис. 20 и 21. Сужение геодезической вблизи полюса исчезает в пределеб → c; в этом случае эллипсоид становится апролатным эллипсоидом, и рис. 20 будет напоминать рис. 10 (повернутый на бок). Все касательные к трансполярной геодезической касаются конфокального двустороннего гиперболоида, который пересекает эллипсоид в точкеω = ω1.

Если отправной точкой является β1 = 90°,ω1 = 0° (пупочная точка), иα1 = 135° (геодезическая выходит из эллипсаY = 0 под прямым углом), тоγ = 0 и геодезическая многократно пересекает противоположную точку пуповины и возвращается в свою исходную точку. Однако на каждом контуре угол, под которым он пересекаетY = 0 становится ближе к 0° или же180° так что асимптотически геодезическая лежит на эллипсе Y = 0 (Харт 1849 ) (Арнольд 1989, п. 265), как показано на рис. 22. Отдельная геодезическая не заполняет область на эллипсоиде. Все касательные к пуповинным геодезическим касаются софокусной гиперболы, которая пересекает эллипсоид в точках пуповины.
Пуповинные геодезические обладают несколькими интересными свойствами.
- Через любую точку эллипсоида проходят две омбилические геодезические.
- Геодезическое расстояние между противоположными точками шлангокабеля одинаково независимо от начального направления геодезической.
- Тогда как замкнутые геодезические на эллипсах Икс = 0 и Z = 0 устойчивы (геодезическая, изначально близкая к эллипсу и почти параллельная ему, остается близкой к эллипсу), замкнутая геодезическая на эллипсе Y = 0, который проходит через все 4 точки пуповины, экспоненциально нестабильный. Если его потревожить, он вылетит из плоскости Y = 0 и перевернитесь, прежде чем вернуться, чтобы приблизиться к самолету. (Это поведение может повторяться в зависимости от природы начального возмущения.)
Если отправная точка А геодезической не является точкой пупка, ее оболочка - астроида с двумя вершинами, лежащими наβ = −β1 и два других наω = ω1 + π. Место разреза А это часть строки β = −β1 между бугорками.
Приложения
Прямая и обратная геодезические задачи больше не играют центральной роли в геодезии, как раньше. Вместо решениякорректирование из геодезические сети как двумерная задача в сфероидальной тригонометрии, эти задачи теперь решаются трехмерными методами (Винсенти и Боуринг 1978 Тем не менее, земные геодезические по-прежнему играют важную роль в нескольких областях:
- для измерения расстояний и площадей в географические информационные системы;
- определение морские границы (ЮНКЛОС 2006 г. );
- в правилах Федеральная авиационная администрация для зональной навигации (RNAV 2007 );
- метод измерения расстояний в FAI Спортивный кодекс (FAI 2018 ).
- помочь мусульманам найти их направление в сторону Мекки
Посредством принцип наименьшего действия многие задачи физики могут быть сформулированы как вариационные задачи, аналогичные задачам геодезических. В самом деле, геодезическая задача эквивалентна движению частицы, вынужденной двигаться по поверхности, но в остальном не подверженной никаким силам (Лаплас 1799a ) (Гильберт и Кон-Фоссен, 1952 г., п. 222). По этой причине геодезические на простых поверхностях, таких как эллипсоиды вращения или трехосные эллипсоиды, часто используются в качестве «тестовых примеров» для изучения новых методов. Примеры включают:
- развитие эллиптических интегралов (Legendre 1811 г. ) и эллиптические функции (Вейерштрасс 1861 );
- развитие дифференциальной геометрии (Гаусс 1828 г. ) (Кристоффель 1869 );
- методы решения систем дифференциальных уравнений заменой независимых переменных (Якоби 1839 );
- изучение каустика (Якоби 1891 );
- исследования числа и устойчивости периодических орбит (Пуанкаре 1905 );
- в пределе c → 0геодезические на трехосном эллипсоиде сводятся к случаю динамический бильярд;
- расширения на произвольное количество измерений (Knörrer 1980 );
- геодезический поток на поверхности (Бергер 2010, Гл. 12).
Смотрите также
- Фигура Земли
- Географическое расстояние
- Навигация по большому кругу
- Большой эллипс
- Геодезические
- Геодезия
- Дуга меридиана
- Линия румба
- Формулы Винсенти
Примечания
- ^ Здесь α2 это вперед азимут на BНекоторые авторы рассчитывают назад азимут вместо; это даетсяα2 ± π.
- ^ Лаплас (1799a) showed that a particle constrained to move ona surface but otherwise subject to no forces moves along a geodesic forthat surface. Thus, Clairaut's relation is just a consequence ofсохранение углового момента for a particle on a surface ofrevolution.
- ^ Bagratuni (1962, §17) uses the term "coefficient ofconvergence of ordinates" for the geodesic scale.
- ^ This section is adapted from the documentation for GeographicLib(Karney 2015, Геодезические на трехосном эллипсоиде )
- ^ This notation for the semi-axes is incompatible with that used in theprevious section on ellipsoids of revolution in which а иб stood for the equatorial radius and polar semi-axis.Thus the corresponding inequalities are а = а ≥ б > 0 foran oblate ellipsoid and б ≥ а = а > 0 for a prolateellipsoid.
- ^ Лимит б → c gives a prolate ellipsoid withω playing the role of the parametric latitude.
- ^ Если c⁄а < 1⁄2, there are other simple closed geodesicssimilar to those shown in Figs. 11 and 12(Klingenberg 1982, §3.5.19).
Рекомендации
- Арнольд, В.И. (1989). Математические методы классической механики. Translated by Vogtmann, K.; Weinstein, A. (2nd ed.). Springer-Verlag. ISBN 978-0-387-96890-2. OCLC 4037141.CS1 maint: ref = harv (связь)
- Bagratuni, G. V. (1967) [1962]. Course in Spheroidal Geodesy. Дои:10.5281/zenodo.32371. OCLC 6150611. Translation from Russian of Курс сфероидической геодезии (Moscow, 1962) by U.S. Air Force (FTD-MT-64-390 )
- Berger, M. (2010). Geometry Revealed. Translated by Senechal, L. J. Springer. Дои:10.1007/978-3-540-70997-8. ISBN 978-3-540-70996-1.CS1 maint: ref = harv (связь)
- Бессель, Ф. В. (2010) [1825]. Translated by Karney, C. F. F.; Deakin, R. E. "The calculation of longitude and latitude from geodesic measurements". Astronomische Nachrichten. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN .... 331..852K. Дои:10.1002 / asna.201011352. Английский перевод Astron. Nachr. 4, 241–254 (1825). Опечатки.
- Bliss, G. A. (1916). "Jacobi's condition for problems of the calculus of variations in parametric form". Труды Американского математического общества. 17 (2): 195–206. Дои:10.1090/S0002-9947-1916-1501037-4 (free access).CS1 maint: ref = harv (связь)
- Bomford, G. (1952). Геодезия. Оксфорд: Кларендон. OCLC 1396190.CS1 maint: ref = harv (связь)
- Borre, K.; Strang, W. G. (2012). Algorithms for Global Positioning. Wellesley-Cambridge Press. ISBN 978-0-9802327-3-8. OCLC 795014501. Chapter 11, Geometry of the Ellipsoid.CS1 maint: ref = harv (связь)
- Кэли, А. (1870). "On the geodesic lines on an oblate spheroid". Философский журнал. 4-я серия. 40 (268): 329–340. Дои:10.1080/14786447008640411.CS1 maint: ref = harv (связь)
- Chasles, M. (1846). "Sur les lignes géodésiques et les lignes de courbure des surfaces du second degré" [Geodesic lines and the lines of curvature of the surfaces of the second degree] (PDF). Journal de Mathématiques Pures et Appliquées (На французском). 11: 5–20.CS1 maint: ref = harv (связь)
- Christoffel, E. B. (1869). "Allgemeine Theorie der geodätischen Dreiecke" [General theory of geodesic triangles]. Abhandlungen Königlichen Akademie der Wissenschaft zu Berlin (in German): 119–176.CS1 maint: ref = harv (связь)
- Clairaut, A. C. (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Geometrical determination of the perpendicular to the meridian drawn by Jacques Cassini]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (in French): 406–416.CS1 maint: ref = harv (связь)
- Danielsen, J. S. (1989). "The Area under the Geodesic". Обзор обзора. 30 (232): 61–66. Дои:10.1179/003962689791474267.CS1 maint: ref = harv (связь)
- Darboux, J. G. (1894). Leçons sur la théorie générale des surfaces [Lessons on the general theory of surfaces] (На французском). 3. Париж: Готье-Виллар. OCLC 8566228. PDF.CS1 maint: ref = harv (связь)
- Dupin, P. C. F. (1813). Développements de Géométrie [Developments in geometry] (На французском). Париж: Курсье. OCLC 560800801.CS1 maint: ref = harv (связь)
- Ehlert, D. (1993). Methoden der ellipsoidischen Dreiecksberechnung [Methods for ellipsoidal triangulation] (Technical report). Reihe B: Angewandte Geodäsie, Heft Nr. 292 (in German). Deutsche Geodätische Kommission. OCLC 257615376.CS1 maint: ref = harv (связь)
- Эйлер, Л. (1755). "Élémens de la trigonométrie sphéroïdique tirés de la méthode des plus grands et plus petits" [Elements of spheroidal trigonometry taken from the method of maxima and minima]. Mémoires de l'Académie Royale des Sciences de Berlin 1753 (На французском). 9: 258–293. Цифры.CS1 maint: ref = harv (связь)
- FAI (2018). FAI Sporting Code (PDF) (Технический отчет). Лозанна, Швейцария: Международная авиационная федерация. Section 8.2.3.CS1 maint: ref = harv (связь)
- Forsyth, A. R. (1927). Calculus of Variations. Cambridge Univ. Нажмите. ISBN 978-1-107-64083-2. OCLC 250050479.CS1 maint: ref = harv (связь)
- Gan'shin, V. V. (1969) [1967]. Geometry of the Earth Ellipsoid. Translated by Willis, J. M. St. Louis: Aeronautical Chart and Information Center. Дои:10.5281/zenodo.32854. OCLC 493553. Translation from Russian of Геометрия земного эллипсоида (Moscow, 1967).
- Гаусс, К.Ф. (1902) [1828]. General Investigations of Curved Surfaces of 1827 and 1825. Translated by Morehead, J. C.; Hiltebeitel, A. M. Princeton Univ. Lib. OCLC 7824448. PDF. Английский перевод Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828).
- Hart, A. S. (1849). "Geometrical demonstration of some properties of geodesic lines". Кембриджский и Дублинский математический журнал. 4: 80–84.CS1 maint: ref = harv (связь)
- Helmert, F. R. (1964) [1880]. Математические и физические теории высшей геодезии. 1. St. Louis: Aeronautical Chart and Information Center. Дои:10.5281/zenodo.32050. OCLC 17273288. Английский перевод Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, Vol. 1 (Teubner, Leipzig, 1880).
- Hilbert, D.; Cohn-Vossen, S. (1952). Геометрия и воображение. Translated by Nemenyi, P. New York: Chelsea. OCLC 301610346.CS1 maint: ref = harv (связь)
- Hutton, C. (1811). A Course of Mathematics in Three Volumes Composed for the Use of the Royal Military Academy. Лондон: Ф. К. и Дж. Ривингтон. п.115. OCLC 18031510.CS1 maint: ref = harv (связь)
- Jacobi, C. G. J. (1837). "Zur Theorie der Variations-Rechnung und der Differential-Gleichungen" [The theory of the calculus of variations and of differential equations]. Journal für die Reine und Angewandte Mathematik (на немецком). 1837 (17): 68–82. Дои:10.1515/crll.1837.17.68.CS1 maint: ref = harv (связь)
- Jacobi, C. G. J. (1839). "Note von der geodätischen Linie auf einem Ellipsoid und den verschiedenen Anwendungen einer merkwürdigen analytischen Substitution" [The geodesic on an ellipsoid and various applications of a remarkable analytical substitution]. Journal für die Reine und Angewandte Mathematik (на немецком). 1839 (19): 309–313. Дои:10.1515/crll.1839.19.309. Letter to Bessel, Dec. 28, 1838. французский перевод (1841).CS1 maint: ref = harv (связь)
- Jacobi, C. G. J. (2009) [1866]. A. Clebsch (ред.). Lectures on Dynamics. Translated by Balagangadharan, K. New Delhi: Hindustan Book Agency. ISBN 978-81-85931-91-3. МИСТЕР 2569315. OCLC 440645889. Английский перевод Vorlesungen über Dynamik (Reimer, Berlin, 1866). Опечатки.
- Jacobi, C. G. J. (1891). "Über die Curve, welche alle von einem Punkte ausgehenden geodätischen Linien eines Rotationsellipsoides berührt" [The envelope of geodesic lines emanating from a single point on an ellipsoid]. В K. T. W. Weierstrass (ред.). Jacobi's Gesammelte Werke (на немецком). 7. Berlin: Reimer. С. 72–87. OCLC 630416023. Соч. post., completed by F. H. A. Wangerin. PDF.CS1 maint: ref = harv (связь)
- Jekeli, C. (2012), Geometric Reference Systems in Geodesy, Ohio State Univ., HDL:1811/51274CS1 maint: ref = harv (связь)
- Jordan, W.; Eggert, O. (1962) [1941]. Handbook of Geodesy. 3.2. Translated by Carta, M. W. Washington, DC: Army Map Service. Bibcode:1962hage.book.....J. Дои:10.5281/zenodo.35316. OCLC 34429043. Английский перевод Handbuch der Vermessungskunde, 8th edition (Metzler, Stuttgart, 1941).
- Карни, К. Ф. Ф. (2013). «Алгоритмы геодезических». Журнал геодезии. 87 (1): 43–55. arXiv:1109.4448. Bibcode:2013JGeod..87 ... 43K. Дои:10.1007 / s00190-012-0578-z (open access). Дополнения.CS1 maint: ref = harv (связь)
- Karney, C. F. F. (2015). "GeographicLib". Version 1.44.CS1 maint: ref = harv (связь)
- Klingenberg, W. P. A. (1982). Риманова геометрия. de Gruyer. ISBN 978-3-11-008673-7. МИСТЕР 0666697. OCLC 8476832.CS1 maint: ref = harv (связь)
- Knörrer, H. (1980). "Geodesics on the ellipsoid". Inventiones Mathematicae. 59 (2): 119–143. Bibcode:1980InMat..59..119K. Дои:10.1007/BF01390041.CS1 maint: ref = harv (связь)
- Krakiwsky, E. J.; Thomson, D. B. (1974), Geodetic position computations (PDF), Dept. of Geodesy and Geomatics Engineering, Lecture Notes, Fredericton, N.B.: Univ. of New Brunswick, Bibcode:1974gpc..book.....KCS1 maint: ref = harv (связь)
- Laplace, P. S. (1829) [1799a]. Treatise on Celestial Mechanics. 1. Переведено Bowditch, N. Boston: Hillard, Gray, Little, & Wilkins. OCLC 1294937. Book 1, §8.
- Laplace, P. S. (1799b). Traité de Mécanique Céleste [Treatise on Celestial Mechanics] (На французском). 2. Париж: Крепелет. п. 112. OCLC 25448952.CS1 maint: ref = harv (связь)
- Legendre, A. M. (1806). "Analyse des triangles tracées sur la surface d'un sphéroïde" [Analysis of spheroidal triangles]. Mémoires de l'Institut National de France (in French) (1st semester): 130–161.CS1 maint: ref = harv (связь)
- Legendre, A. M. (1811). Exercices de Calcul Intégral sur Divers Ordres de Transcendantes et sur les Quadratures [Exercises in Integral Calculus] (На французском). Париж: Курсье. OCLC 312469983.CS1 maint: ref = harv (связь)
- Leick, A.; Rapoport, L.; Tatarnikov, D. (2015). GPS Satellite Surveying (4-е изд.). Вайли. ISBN 978-1-119-01828-5.
- Liouville, J. (1846). "Sur quelques cas particuliers où les équations du mouvement d'un point matériel peuvent s'intégrer" [On special cases where the equations of motion of a point particle can be integrated] (PDF). Journal de Mathématiques Pures et Appliquées (На французском). 11: 345–378.CS1 maint: ref = harv (связь)
- Lyusternik, L. (1964). Shortest Paths: Variational Problems. Popular Lectures in Mathematics. 13. Translated by Collins, P.; Brown, R. B. New York: Macmillan. МИСТЕР 0178386. OCLC 1048605. Translation from Russian of Кратчайшие Линии: Вариационные Задачи (Moscow, 1955).CS1 maint: ref = harv (связь)
- Monge, G. (1850) [1796]. "Sur les lignes de courbure de la surface de l'ellipsoïde" [On the lines of curvature on the surface of the ellipsoid]. В J. Liouville (ред.). Application de l'Analyse à la Géometrie (in French) (5th ed.). Париж: Башелье. pp. 139–160. OCLC 2829112. Цифры.
- Национальная геодезическая служба (2012). "Geodesic Utilities: Inverse and Forward". Version 3.0.
- Ньютон, И. (1848) [1687]. Математические основы естественной философии. Translated by Motte, A. New York: Adee. п.405. Book 3, Proposition 19, Problem 3, pp. 405–409.
- Oriani, B. (1806). "Elementi di trigonometria sferoidica, Pt. 1" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (на итальянском). 1 (1): 118–198.CS1 maint: ref = harv (связь)
- Oriani, B. (1808). "Elementi di trigonometria sferoidica, Pt. 2" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (на итальянском). 2 (1): 1–58.CS1 maint: ref = harv (связь)
- Oriani, B. (1810). "Elementi di trigonometria sferoidica, Pt. 3" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (на итальянском). 2 (2): 1–58.CS1 maint: ref = harv (связь)
- Poincaré, H. (1905). "Sur les lignes géodésiques des surfaces convexes" [Geodesics lines on convex surfaces]. Труды Американского математического общества (На французском). 6 (3): 237–274. Дои:10.2307/1986219. JSTOR 1986219.CS1 maint: ref = harv (связь)
- Rainsford, H. F. (1955). "Long geodesics on the ellipsoid". Bulletin Géodésique. 37 (1): 12–22. Bibcode:1955BGeod..29...12R. Дои:10.1007/BF02527187.CS1 maint: ref = harv (связь)
- Rapp, R. H. (1991), Geometric geodesy, part I, Ohio State Univ., HDL:1811/24333CS1 maint: ref = harv (связь)
- Rapp, R. H. (1993), Geometric geodesy, part II, Ohio State Univ., HDL:1811/24409CS1 maint: ref = harv (связь)
- RNAV (2007). Order 8260.54A, The United States Standard for Area Navigation (PDF) (Технический отчет). Washington, D.C.: U.S. Federal Aviation Administration. Приложение 2.CS1 maint: ref = harv (связь)
- Sjöberg, L. E. (2006). "Determination of areas on the plane, sphere and ellipsoid". Обзор обзора. 38 (301): 583–593. Дои:10.1179/003962606780732100.CS1 maint: ref = harv (связь)
- ЮНКЛОС (2006). A Manual on Technical Aspects of the United Nations Convention on the Law of the Sea, 1982 (PDF) (Technical report) (4th ed.). Монако: Международное гидрографическое бюро.CS1 maint: ref = harv (связь)
- Vincenty, T. (1975). "Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations" (PDF). Обзор обзора. 23 (176): 88–93. Дои:10.1179/sre.1975.23.176.88. Addendum: Survey Review 23 (180): 294 (1976).CS1 maint: ref = harv (связь)
- Vincenty, T.; Bowring, B. R. (1978). Application of three-dimensional geodesy to adjustments of horizontal networks (PDF) (Технический отчет). NOAA. NOS NGS-13.CS1 maint: ref = harv (связь)
- Weierstrass, K. T. W. (1861). "Über die geodätischen Linien auf dem dreiaxigen Ellipsoid" [Geodesic lines on a triaxial ellipsoid]. Monatsberichte der Königlichen Akademie der Wissenschaft zu Berlin (in German): 986–997. PDF.CS1 maint: ref = harv (связь)
внешняя ссылка
- Online geodesic bibliography of books and articles on geodesics on ellipsoids.
- Test set for geodesics, a set of 500000 geodesics for the WGS84 ellipsoid, computed using high-precision arithmetic.
- NGS tool реализация Vincenty (1975).
- geod(1), man page for the ПРОЕКТ utility for geodesic calculations.
- GeographicLib implementation из Karney (2013).
- Drawing geodesics on Google Maps.


































![{ displaystyle { begin {align} delta & = int { frac {{ sqrt {b ^ {2} sin ^ {2} beta + c ^ {2} cos ^ {2} beta }} , d beta} {{ sqrt {a ^ {2} -b ^ {2} sin ^ {2} beta -c ^ {2} cos ^ {2} beta}} { sqrt {{ bigl (} b ^ {2} -c ^ {2} { bigr)} cos ^ {2} beta - gamma}}}} [6pt] & quad - int { frac {{ sqrt {a ^ {2} sin ^ {2} omega + b ^ {2} cos ^ {2} omega}} , d omega} {{ sqrt {a ^ { 2} sin ^ {2} omega + b ^ {2} cos ^ {2} omega -c ^ {2}}} { sqrt {{ bigl (} a ^ {2} -b ^ { 2} { bigr)} sin ^ {2} omega + gamma}}}}. End {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b5c88b1ff894b8ebb8772e0a41e8a6d2c37094)
