Белтрами личность - Beltrami identity

Эухенио Бельтрами

В Белтрами личность, названный в честь Эухенио Бельтрами, является частным случаем Уравнение Эйлера – Лагранжа. в вариационное исчисление.

Уравнение Эйлера – Лагранжа служит для ограничения действия функционалы формы

${ displaystyle I [u] = int _ {a} ^ {b} L [x, u (x), u '(x)] , dx ,,}$

куда ${ displaystyle a}$ и ${ displaystyle b}$ константы и ${ displaystyle u '(x) = { frac {du} {dx}}}$.^[1]

Если ${ displaystyle { frac { partial L} { partial x}} = 0}$, то уравнение Эйлера – Лагранжа сводится к тождеству Бельтрами:

куда C является константой.^{[2][примечание 1]}

Вывод

Следующий вывод тождества Бельтрами начинается с уравнения Эйлера – Лагранжа,

${ displaystyle { frac { partial L} { partial u}} = { frac {d} {dx}} { frac { partial L} { partial u '}} ,.}$

Умножая обе стороны на ты′,

${ displaystyle u '{ frac { partial L} { partial u}} = u' { frac {d} {dx}} { frac { partial L} { partial u '}} ,. }$

Согласно Правило цепи,

${ displaystyle {dL over dx} = { partial L over partial u} u '+ { partial L over partial u'} u '' + { partial L over partial x} , ,}$

куда ${ displaystyle u '' = { frac {du '} {dx}} = { frac {d ^ {2} u} {dx ^ {2}}}}$.

Перестановка этого урожая

${ displaystyle u '{ partial L over partial u} = {dL over dx} - { partial L over partial u'} u '' - { partial L over partial x} , .}$

Таким образом, подставляя это выражение вместо ${ displaystyle u '{ frac { partial L} { partial u}}}$во второе уравнение этого вывода,

${ displaystyle {dL over dx} - { partial L over partial u '} u' '- { partial L over partial x} -u' { frac {d} {dx}} { frac { partial L} { partial u '}} = 0 ,.}$

По правилу продукта последний член повторно выражается как

${ displaystyle u '{ frac {d} {dx}} { frac { partial L} { partial u'}} = { frac {d} {dx}} left ({ frac { partial L} { partial u '}} u' right) - { frac { partial L} { partial u '}} u' ' ,,}$

и переставляя,

${ displaystyle {d over dx} left ({L-u '{ frac { partial L} { partial u'}}} right) = { partial L over partial x} ,. }$

В случае ${ displaystyle { frac { partial L} { partial x}} = 0}$, это сводится к

${ displaystyle {d over dx} left ({L-u '{ frac { partial L} { partial u'}}} right) = 0 ,,}$

так что принимая первообразный приводит к идентичности Бельтрами,

${ displaystyle L-u '{ frac { partial L} { partial u'}} = C ,,}$

куда C является константой.^[3]

Приложения

Решение проблемы брахистохрона

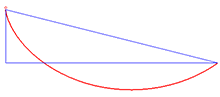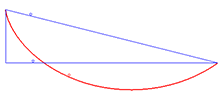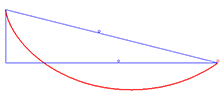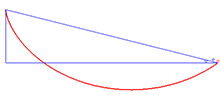
Решение проблемы брахистохрона - это циклоида.

Примером применения идентичности Бельтрами является проблема брахистохрона, что предполагает нахождение кривой ${ Displaystyle у = у (х)}$ что минимизирует интеграл

${ displaystyle I [y] = int _ {0} ^ {a} { sqrt {{1 + y '^ {, 2}} over y}} dx ,.}$

Подынтегральное выражение

${ Displaystyle L (y, y ') = { sqrt {{1 + y' ^ {, 2}} над y}}}$

не зависит явно от переменной интегрирования ${ displaystyle x}$, поэтому применяется идентичность Бельтрами,

${ displaystyle L-y '{ frac { partial L} { partial y'}} = C ,.}$

Замена на ${ displaystyle L}$ и упрощая,

${ Displaystyle у (1 + Y '^ {, 2}) = 1 / C ^ {2} ~~ { text {(константа)}} ,,}$

которую можно решить, задав результат в виде параметрические уравнения

${ Displaystyle х = А ( фи - грех фи)}$

${ Displaystyle у = А (1- соз фи)}$

с ${ displaystyle A}$ будучи половиной вышеуказанной константы, ${ displaystyle { frac {1} {2C ^ {2}}}}$, и ${ displaystyle phi}$ быть переменной. Это параметрические уравнения для циклоида.^[4]

Примечания

Рекомендации