Гомография - Википедия - Homography

В проективная геометрия, а омография является изоморфизм из проективные пространства, индуцированный изоморфизмом векторные пространства из которых происходят проективные пространства.^[1] Это биекция что отображает линии к линиям, и, следовательно, коллинеация. В общем, некоторые коллинеации не являются омографиями, но основная теорема проективной геометрии утверждает, что это не так в случае реальных проективных пространств размерности не менее двух. Синонимы включают проективность, проективное преобразование, и проективная коллинеация.

Исторически гомографии (и проективные пространства) были введены для изучения перспектива и прогнозы в Евклидова геометрия, а срок омография, что этимологически примерно означает «подобный рисунок», восходит к этому времени. В конце XIX века были введены формальные определения проективных пространств, которые отличались от расширенных Евклидово или же аффинные пространства добавляя указывает на бесконечность. Термин «проективное преобразование» возник в этих абстрактных конструкциях. Эти конструкции делятся на два класса, которые оказались эквивалентными. Проективное пространство может быть построено как множество прямых векторное пространство над данным поле (приведенное выше определение основано на этой версии); эта конструкция облегчает определение проективные координаты и позволяет использовать инструменты линейная алгебра для изучения омографий. Альтернативный подход состоит в определении проективного пространства с помощью набора аксиом, которые не включают явно какое-либо поле (геометрия падения, смотрите также синтетическая геометрия ); в этом контексте коллинеации легче определить, чем омографии, а омографии определяются как специфические коллинеации, так называемые «проективные коллинеации».

Для простоты, если не указано иное, проективные пространства, рассматриваемые в этой статье, должны быть определены над (коммутативным) поле. Эквивалентно Теорема Паппа о шестиугольнике и Теорема дезарга должны быть правдой. Большая часть результатов остается верной или может быть обобщена на проективные геометрии, для которых эти теоремы не верны.

Геометрическая мотивация

Точки A, B, C, D и A ′, B ′, C ′, D ′ связаны перспективностью, которая является проективным преобразованием.

Исторически концепция гомографии была введена для понимания, объяснения и изучения визуальная перспектива, и, в частности, различие во внешнем виде двух плоских объектов, рассматриваемых с разных точек зрения.

В трехмерном евклидовом пространстве a центральная проекция с точки О (центр) на плоскость п что не содержит О отображение, которое отправляет точку А до пересечения (если есть) прямой OA и самолет п. Проекция не определяется, если точка А принадлежит самолету, проходящему через О и параллельно п. Понятие проективное пространство был первоначально введен путем расширения евклидова пространства, то есть путем добавления указывает на бесконечность к нему, чтобы определить проекцию для каждой точки, кроме О.

Учитывая другой самолет Q, который не содержит О, то ограничение к Q проекции выше называется перспективность.

С этими определениями перспективность - это только частичная функция, но становится биекция если распространить на проективные пространства. Поэтому это понятие обычно определяется для проективных пространств. Это понятие также легко обобщается на проективные пространства любой размерности, над любым поле, следующим образом:

Учитывая два проективных пространства п и Q измерения п, а перспективность это биекция от п к Q что может быть получено вложением п и Q в проективном пространстве р измерения п + 1 и ограничиваясь п центральная проекция на Q.

Если ж перспектива от п к Q, и грамм перспектива от Q к п, с другим центром, то грамм ⋅ ж это омография от п самому себе, что называется центральная коллинеация, когда размерность п как минимум два. (видеть § Центральные коллинеации ниже и Перспективность § Перспективные коллинеации ).

Первоначально омография был определен как сочинение конечного числа перспектив.^[2] Это часть фундаментальной теоремы проективной геометрии (см. Ниже), что это определение совпадает с более алгебраическим определением, набросанным во введении и подробно описанным ниже.

Определение и выражение в однородных координатах

А проективное пространство П(V) размерности п через поле K можно определить как набор линий, проходящих через начало координат в K-векторное пространство V измерения п + 1. Если на основе V был исправлен, точка V может быть представлен точкой ${ displaystyle (x_ {0}, ldots, x_ {n})}$ из K^п+1. Точка P (V), являясь линией в V, таким образом, могут быть представлены координатами любой ненулевой точки этой линии, которые, таким образом, называются однородные координаты проективной точки.

Для двух проективных пространств P (V) и P (W) того же размера, омография отображение из P (V) верх(W), которое индуцировано изоморфизм векторных пространств ${ displaystyle f: V rightarrow W}$ . Такой изоморфизм индуцирует биекция из P (V) верх(W) из-за линейности ж. Два таких изоморфизма, ж и грамм, определим ту же гомографию тогда и только тогда, когда существует ненулевой элемент а из K такой, что грамм = аф.

Это можно записать в терминах однородных координат следующим образом: гомография φ может быть определен неособый п+1 × п+1 матрица [а_я,j], называется матрица гомографии. Эта матрица определяется вплоть до умножение на ненулевой элемент K. Однородные координаты ${ displaystyle [x_ {0}: cdots: x_ {n}]}$ точки и координаты ${ displaystyle [y_ {0}: cdots: y_ {n}]}$ своего имиджа φ связаны

{ displaystyle { begin {align} y_ {0} & = a_ {0,0} x_ {0} + dots + a_ {0, n} x_ {n} & vdots y_ {n} & = a_ {n, 0} x_ {0} + dots + a_ {n, n} x_ {n}. end {align}}}

Когда проективные пространства определены добавлением указывает на бесконечность к аффинные пространства (проективное пополнение) предыдущие формулы становятся в аффинных координатах

{ displaystyle { begin {align} y_ {1} & = { frac {a_ {1,0} + a_ {1,1} x_ {1} + dots + a_ {1, n} x_ {n}) } {a_ {0,0} + a_ {0,1} x_ {1} + dots + a_ {0, n} x_ {n}}} & vdots y_ {n} & = { гидроразрыв {a_ {n, 0} + a_ {n, 1} x_ {1} + dots + a_ {n, n} x_ {n}} {a_ {0,0} + a_ {0,1} x_ { 1} + точки + a_ {0, n} x_ {n}}} end {выровнены}}}

который обобщает выражение гомографической функции следующего раздела. Это определяет только частичная функция между аффинными пространствами, который определен только вне гиперплоскость где знаменатель равен нулю.

Омографии проективной прямой

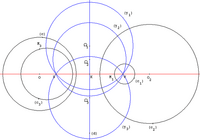
Гомографии комплексная плоскость сохранить ортогональные окружности

Проективная прямая над поле K можно отождествить с союзом K и точка, называемая «бесконечно удаленной точкой» и обозначаемая ∞ (см. проективная линия ). При таком представлении проективной прямой омографии - это отображения

{ displaystyle z mapsto { frac {az + b} {cz + d}}, { text {where}} ad-bc neq 0,}

которые называются гомографические функции или же дробно-линейные преобразования.

В случае сложная проективная линия, который можно отождествить с Сфера Римана, омографии называются Преобразования Мебиуса Они точно соответствуют тем биекциям сферы Римана, которые сохраняют ориентацию и являются конформными.^[3]

При изучении коллинеаций случай проективных прямых является особенным из-за малой размерности. Когда линия рассматривается как изолированное проективное пространство, любые перестановка точек проективной прямой - коллинеация,^[4] поскольку каждый набор точек коллинеарен. Однако, если проективная линия вложена в проективное пространство более высокой размерности, геометрическая структура этого пространства может быть использована для наложения геометрической структуры на линию. Таким образом, в синтетической геометрии рассматриваемые омографии и коллинеации проективной прямой получаются ограничениями на линию коллинеаций и омографий пространств более высокой размерности. Это означает, что основная теорема проективной геометрии (см. Ниже) остается верной в одномерном случае. Гомографию проективной прямой также можно правильно определить, настаивая на том, что отображение сохраняет перекрестные отношения.^[5]

Проективная рамка и координаты

А проекционная рамка или же проективная основа проективного пространства размерности $п$ упорядоченный набор $п + 2$ такие точки, что ни одна гиперплоскость не содержит $п + 1$ их. Проективный фрейм иногда называют симплекс,^[6] хотя симплекс в пространстве измерения $п$ имеет самое большее $п + 1$ вершины.

Проективные пространства над коммутативным полем $K$ рассматриваются в этом разделе, хотя большинство результатов можно обобщить на проективные пространства над делительное кольцо.

Позволять $п (V)$ быть проективным пространством размерности $п$ , куда $V$ это $K$ -векторное пространство измерения $п + 1$ , и ${ displaystyle p: V setminus {0 } to P (V)}$ - каноническая проекция, отображающая ненулевой вектор в векторную линию, которая его содержит.

Для каждого кадра $п (V)$ , существует основа ${ displaystyle e_ {0}, dots, e_ {n}}$ из $V$ такой, что рамка ${ displaystyle left (p (e_ {0}), ldots, p (e_ {n}), p (e_ {0} + dots + e_ {n}) right),}$ и этот базис уникален с точностью до умножения всех его элементов на один и тот же ненулевой элемент из $K$ . Наоборот, если ${ displaystyle e_ {0}, dots, e_ {n}}$ является основой $V$ , тогда ${ displaystyle left (p (e_ {0}), ldots, p (e_ {n}), p (e_ {0} + dots + e_ {n}) right)}$ это рамка $п (V)$

Отсюда следует, что для данных двух фреймов существует ровно одна гомография, отображающая первую во вторую. В частности, единственной гомографией, фиксирующей точки кадра, является карта идентичности. Этот результат намного сложнее в синтетическая геометрия (где проективные пространства определены через аксиомы). Иногда его называют первая основная теорема проективной геометрии.^[7]

Каждый кадр ${ displaystyle (p (e_ {0}), ldots, p (e_ {n}), p (e_ {0} + cdots + e_ {n}))}$ позволяет определить проективные координаты, также известный как однородные координаты: каждая точка может быть записана как $п (v)$ ; проективные координаты $п (v)$ на этом кадре координаты $v$ на базе ${ displaystyle (e_ {0}, ldots, e_ {n}).}$ Нетрудно убедиться, что изменение ${ displaystyle e_ {i}}$ и $v$ , без изменения кадра и п(v), приводит к умножению проективных координат на тот же ненулевой элемент K.

Проективное пространство $п п (K) = п (K п +1)$ имеет каноническая рамка состоящий из изображения $п$ канонической основы $K п +1$ (состоящий из элементов, имеющих только одну ненулевую запись, равную 1), и $(1, 1, ..., 1)$ . Исходя из этого, однородные координаты $п (v)$ являются просто элементами (коэффициентами) кортеж $v$ . Учитывая другое проективное пространство $п (V)$ того же размера, и рама $F$ из него есть одна и только одна омография $час$ отображение $F$ на канонические рамки $п п (K)$ . Проективные координаты точки $а$ на раме $F$ - однородные координаты $час (а)$ на канонической основе $п п (K)$ .

Центральные коллинеации

Точки A, B, C, D и A ′, B ′, C ′, D ′ связаны несколькими центральными коллинеациями, которые полностью задаются путем выбора линии неподвижных точек L, проходящей через пересечение прямых ABCD и A ′ B′C′D ′. Пусть O - пересечение прямых AA ′, BB ′, CC ′, DD ′. Изображение E ′ точки E на этой коллинеации является пересечением прямых A′I и OE, где I - пересечение прямых L и AE.

В приведенных выше разделах омографии были определены с помощью линейной алгебры. В синтетическая геометрия, их традиционно определяют как композицию одной или нескольких специальных омографий, называемых центральные коллинеации. То, что эти два определения эквивалентны, является частью основной теоремы проективной геометрии.

В проективном пространстве п, размерности п ≥ 2, а коллинеация из п это биекция от п на п который отображает линии на линии. А центральная коллинеация (традиционно их называли перспективы,^[8] но этот термин может сбивать с толку, имея другое значение; видеть Перспективность ) является биекцией α из п к п, такое, что существует гиперплоскость ЧАС (называется ось из α), который поточечно фиксируется α (то есть, α(Икс) = Икс по всем пунктам Икс в ЧАС) и точка О (называется центр из α), которая линейно фиксируется α (любая линия через О отображается на себя α, но не обязательно поточечно).^[9] Есть два типа центральных коллинеаций. Восторги - центральные коллинеации, центр которых падает на ось, а гомологии - это те, в которых центр не соприкасается с осью. Центральная коллинеация однозначно определяется ее центром, осью и изображением. α(п) любой заданной точки п что отличается от центра О и не принадлежит оси. (Изображение α(Q) любой другой точки Q является пересечением прямой, определяемой О и Q и линия, проходящая через α(п) и пересечение с осью линии, определяемой п и Q.)

Центральная коллинеация - это гомография, определяемая (п+1) × (п+1) матрица который имеет собственное подпространство измерения п. Это гомология, если матрица имеет другую собственное значение и поэтому диагонализуемый. Приятно, если все собственные значения равны и матрица не диагонализируется.

Геометрический вид центральной коллинеации легче всего увидеть на проективной плоскости. Учитывая центральную коллинеацию α, рассмотрим прямую ${ displaystyle ell}$ что не проходит через центр О, и его изображение под α, ${ Displaystyle ell '= альфа ( ell)}$ . Параметр ${ Displaystyle R = ell cap ell '}$ , ось α какая-то линия M через р. Изображение любой точки А из ${ displaystyle ell}$ под α это пересечение OA с ${ displaystyle ell '}$ . Изображение B′ Точки B что не принадлежит ${ displaystyle ell}$ можно построить следующим образом: пусть ${ displaystyle S = AB cap M}$ , тогда ${ displaystyle B '= SA' cap OB}$ .

Композиция двух центральных коллинеаций, хотя и остается гомографией в целом, не является центральной коллинеацией. Фактически, каждая гомография - это композиция конечного числа центральных коллинеаций. В синтетической геометрии это свойство, являющееся частью фундаментальной теории проективной геометрии, принимается за определение омографий.^[10]

Основная теорема проективной геометрии

Помимо омографий существуют коллинеации. В частности, любые полевой автоморфизм σ поля F индуцирует коллинеацию каждого проективного пространства над F применяя σ все однородные координаты (над проективным репером) точки. Эти коллинеации называются автоморфные коллинеации.

В основная теорема проективной геометрии состоит из трех следующих теорем.

Даны две проективные шкалы проективного пространства п, существует ровно одна гомография п который отображает первый кадр на второй.
Если размерность проективного пространства п не меньше двух, каждая коллинеация п является композицией автоморфной коллинеации и гомографии. В частности, над вещественными числами каждая коллинеация проективного пространства размерности не менее двух является гомографией.^[11]
Каждая гомография - это композиция конечного числа перспективы. В частности, если размерность подразумеваемого проективного пространства не менее двух, каждая гомография является композицией конечного числа центральных коллинеаций.

Если проективные пространства определены с помощью аксиом (синтетическая геометрия ), третья часть - это просто определение. С другой стороны, если проективные пространства определены с помощью линейная алгебра, первая часть является простым следствием определений. Следовательно, доказательство первой части в синтетической геометрии и доказательство третьей части в терминах линейной алгебры являются фундаментальными шагами доказательства эквивалентности двух способов определения проективных пространств.

Гомографические группы

Поскольку каждая омография имеет обратное отображение и сочинение двух омографий является другим, гомографии данного проективного пространства образуют группа. Например, Группа Мебиуса группа гомографии любой комплексной проективной прямой.

Поскольку все проективные пространства одной размерности над одним и тем же полем изоморфны, то же самое верно и для их групп гомографии. Поэтому они рассматриваются как единая группа, действующая в нескольких пространствах, и в обозначении появляются только размерность и поле, а не конкретное проективное пространство.

Гомографические группы, также называемые проективные линейные группы обозначаются PGL (п + 1, F) при действии на проективное пространство размерности п над полем F. Приведенное выше определение омографий показывает, что PGL (п + 1, F) можно отнести к факторгруппа GL (п + 1, F) / F^×я, куда GL (п + 1, F) это общая линейная группа из обратимые матрицы, и F^×я группа произведений по ненулевому элементу F единичной матрицы размера (п + 1) × (п + 1).

Когда F это Поле Галуа GF (q), то группа гомографии записывается PGL (п, q). Например, PGL (2, 7) действует в восьми точках проективной прямой над конечным полем GF (7), а PGL (2, 4), который изоморфен переменная группа А₅, - группа гомографии проективной прямой с пятью точками.^[12]

Группа омографии PGL (п + 1, F) является подгруппой группа коллинеации PΓL (п + 1, F) коллинеаций проективного пространства размерности п. Когда точки и линии проективного пространства рассматриваются как блочная конструкция, блоки которого представляют собой наборы точек, содержащихся в строке, группу коллинеаций принято называть группа автоморфизмов конструкции.

Перекрестное соотношение

Использование перекрестные отношения в проективная геометрия для измерения реальных размеров объектов, изображенных на перспективная проекция. A, B, C, D и V - точки на изображении, их расстояние указано в пикселях; A ', B', C 'и D' находятся в реальном мире, их разделение в метрах.

В (1) ширина переулка W вычисляется на основе известной ширины соседних магазинов.
В (2) ширина только одного магазина нужна, потому что точка схода, V видна.

Отношение четырех коллинеарных точек является инвариантом относительно гомографии, которая является фундаментальной для изучения гомографии прямых.

Три отличных точки $а$ , $б$ и $c$ на проективной прямой над полем $F$ образуют проективный каркас этой линии. Таким образом, существует уникальная гомография $час$ этой строки на $F \cup \infty$ что отображает $а$ к $\infty$ , $б$ до 0 и $c$ до 1. Учитывая четвертую точку на той же строке, перекрестное соотношение из четырех точек $а$ , $б$ , $c$ и $d$ , обозначенный $[а, б; c, d]$ , это элемент $час (d)$ из $F \cup \infty$ . Другими словами, если $d$ имеет однородные координаты $[k : 1]$ над проективной рамкой $(а, б, c)$ , тогда $[а, б; c, d] = k$ .^[13]

Над кольцом

Предполагать А это звенеть и U это его группа единиц. Гомографии действуют на проективной прямой над А, написано P (А), состоящий из точек U[а, б] с проективные координаты. Омографии на P (А) описываются матричными отображениями

{ Displaystyle U [z, 1] { begin {pmatrix} a & c b & d end {pmatrix}} = U [za + b, zc + d].}

Когда А это коммутативное кольцо, омография может быть написана

{ Displaystyle г mapsto { гидроразрыва {za + b} {zc + d}} ,}

но в остальном дробно-линейное преобразование рассматривается как эквивалент:

{ Displaystyle U [za + b, zc + d] Thicksim U [(zc + d) ^ {- 1} (za + b), 1].}

Группа гомографии кольца целые числа Z является модульная группа PSL (2, Z). Кольцевые омографии использовались в кватернионный анализ, и с двойные кватернионы облегчить теория винта. В конформная группа пространства-времени можно представить с помощью омографий, где А это композиционная алгебра из бикватернионы.^[14]

Периодические омографии

Омография ${ displaystyle h = { begin {pmatrix} 1 & 1 0 & 1 end {pmatrix}}}$ является периодический когда кольцо Z/пZ (в целые числа по модулю п ) с того времени ${ displaystyle h ^ {n} = { begin {pmatrix} 1 & n 0 & 1 end {pmatrix}} = { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}.}$ Артур Кэли интересовался периодичностью, когда вычислял итерации в 1879 г.^[15]В своем обзоре подхода грубой силы к периодичности омографий, Х. С. М. Коксетер дал этот анализ:

Реальная гомография инволютивна (периода 2) тогда и только тогда, когда а + d = 0. Если периодичность с периодом п > 2, то он эллиптический, и без потери общности считается, что объявление − до н.э = 1. Поскольку характеристические корни суть exp (±hπi/м), куда (час, м) = 1, то след является а + d = 2 cos (hπ/м).^[16]

Смотрите также

W-кривая

Примечания

^ Бергер, Глава 4
^ Meserve 1983 г., стр. 43–4
^ Хартсхорн 1967, п. 138
^ Йель 1968, п. 244, Баер 2005, п. 50, Артин 1957 г., п. 88
^ В более старых трактовках часто встречается требование сохранения гармонических тетрад (гармонических наборов) (четырех коллинеарных точек, поперечное отношение которых равно -1), но это исключает проективные линии, определенные над полями характеристика два и поэтому излишне ограничивает. Видеть Баер 2005, п. 76
^ Баер, п. 66
^ Бергер, Глава 6
^ Йель 1968, п. 224
^ Бойтельшпахер и Розенбаум 1998, п. 96
^ Meserve 1983 г., стр. 43–4
^ Хиршфельд 1979, п. 30
^ Хиршфельд 1979, п. 129
^ Бергер, Глава 6
^ Гомографии ассоциативных композиционных алгебр в Викиучебнике
^ Артур Кэли (1879) «О матрице ${ displaystyle scriptstyle { begin {pmatrix} a & b c & d end {pmatrix}},}$ и его связь с функцией ${ displaystyle scriptstyle { frac {ax + b} {cx + d}}}$ ", Посланник математики 9:104
^ Х. С. М. Коксетер, О периодичности в Математические обзоры

дальнейшее чтение

Патрик дю Валь (1964) Гомографии, кватернионы и вращения, Оксфордские математические монографии, Clarendon Press, Оксфорд, МИСТЕР0169108 .
Гюнтер Эвальд (1971) Геометрия: введение, стр. 263, Бельмонт:Wadsworth Publishing ISBN 0-534-00034-7.

[1] Бергер, Глава 4

[2] Meserve 1983 г., стр. 43–4

[3] Хартсхорн 1967, п. 138

[4] Йель 1968, п. 244, Баер 2005, п. 50, Артин 1957 г., п. 88

[5] В более старых трактовках часто встречается требование сохранения гармонических тетрад (гармонических наборов) (четырех коллинеарных точек, поперечное отношение которых равно -1), но это исключает проективные линии, определенные над полями характеристика два и поэтому излишне ограничивает. Видеть Баер 2005, п. 76

[6] Баер, п. 66

[7] Бергер, Глава 6

[8] Йель 1968, п. 224

[9] Бойтельшпахер и Розенбаум 1998, п. 96

[10] Meserve 1983 г., стр. 43–4

[11] Хиршфельд 1979, п. 30

[12] Хиршфельд 1979, п. 129

[13] Бергер, Глава 6

[14] Гомографии ассоциативных композиционных алгебр в Викиучебнике

[15] Артур Кэли (1879) «О матрице ${ displaystyle scriptstyle { begin {pmatrix} a & b c & d end {pmatrix}},}$ и его связь с функцией ${ displaystyle scriptstyle { frac {ax + b} {cx + d}}}$ ", Посланник математики 9:104

[16] Х. С. М. Коксетер, О периодичности в Математические обзоры

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]