Сеть Clos - Clos network

В области телекоммуникации, а Сеть Clos это своего рода многоступенчатый коммутация цепи сеть, которая представляет собой теоретическую идеализацию практических многоступенчатых систем коммутации. Его изобрел Эдсон Эрвин.[1] в 1938 году и впервые формализована Чарльз Клос (Французское произношение:[aʁl klo])[2]в 1952 г.

Добавляя этапы, сеть Clos уменьшает количество точек пересечения, необходимых для создания большого поперечный переключатель. Топология сети Clos (схема ниже) параметризуется тремя целыми числами п, м, и р: п представляет количество источников, которые поступают в каждый из р входные переключающие ступени; Переключатель каждой ступени входа имеет м магазины; и здесь м перекладины средней ступени.

Коммутация каналов обеспечивает выделенный канал связи для соединения между конечными точками на время соединения. Это приносит в жертву общую доступную пропускную способность, если выделенные соединения используются плохо, но делает соединение и пропускную способность более предсказуемыми и вводит накладные расходы на управление только при инициировании соединений, а не при обработке каждого пакета, как в современных условиях. с коммутацией пакетов сети.

Когда сеть Clos была впервые изобретена, количество точек пересечения было хорошим приближением к общей стоимости системы коммутации. Хотя это было важно для электромеханических поперечин, оно стало менее актуальным с появлением СБИС, в котором межсоединения могут быть реализованы либо непосредственно в кремнии, либо в относительно небольшом кластере плат. С появлением сложных центров обработки данных с огромными структурами межсоединений, каждая из которых основана на волоконно-оптических линиях связи, сети Клоса вновь обрели важность.[3] Подтип сети Clos, сеть Beneš, также недавно нашел применение в машинное обучение.[4]

Топология

Сети Clos имеют три этапа: этап входа, средний этап и этап выхода. Каждый этап состоит из нескольких переключающих панелей (см. Диаграмму ниже), часто называемых просто перекладины. Сеть реализует идеальное перемешивание между этапами. Каждый вызов, поступающий на входной линейный коммутатор, может быть перенаправлен через любой из доступных перекрестных переключателей средней ступени к соответствующему выходному перекрестному переключателю. Перекрестная панель средней ступени доступна для конкретного нового вызова, если и ссылка, соединяющая входной коммутатор с коммутатором средней ступени, и ссылка, соединяющая коммутатор средней ступени с выходным коммутатором, свободны.

Closnetwork.png

Сети Clos определяются тремя целыми числами п, м, и р. п представляет количество источников, которые поступают в каждый из р входные переключатели ступеней. Каждый поперечный переключатель входного каскада имеет м розетки, и есть м перекладины средней ступени. Между каждым переключателем входной ступени и каждым переключателем средней ступени имеется ровно одно соединение. Есть р переключатели выходного каскада, каждый с м входы и п выходы. Каждый переключатель средней ступени подсоединяется ровно один раз к каждому переключателю выходной ступени. Таким образом, стадия входа имеет р переключатели, каждый из которых имеет п входы и м выходы. Средний этап имеет м переключатели, каждый из которых имеет р входы и р выходы. Этап выхода имеет р переключатели, каждый из которых имеет м входы и п выходы.

Характеристики блокировки

Относительные значения м и п определить характеристики блокировки сети Clos.

Строго смысловые неблокирующие сети Clos (м ≥ 2п−1): исходный результат Клоза 1953 г.

Если м ≥ 2п−1 сеть Клоса строгая неблокировка, что означает, что неиспользуемый вход на входном коммутаторе всегда можно подключить к неиспользуемому выходу на выходном коммутаторе, без необходимости переупорядочивать существующие звонки. Этот результат лег в основу классической работы Клоса 1953 года. Предположим, что на входе входного коммутатора имеется свободный вывод, и он должен быть подключен к свободному выводу на конкретном выходном коммутаторе. В худшем случае п-1 другие вызовы активны на рассматриваемом входном коммутаторе, и п-1 другие вызовы активны на рассматриваемом исходящем коммутаторе. Предположим, также в худшем случае, что каждый из этих вызовов проходит через другой коммутатор среднего уровня. Следовательно, в худшем случае 2п−2 переключателя средней ступени не могут передать новый вызов. Следовательно, для обеспечения точной неблокирующей работы требуется еще один переключатель средней ступени, всего 2п−1.

Переставляемая неблокирующая сеть Clos (м ≥ п)

Смотрите также: Неблокирующий переключатель минимального диапазона

Если м ≥ п, сеть Clos переставляемый неблокирующий, что означает, что неиспользуемый вход на входном коммутаторе всегда можно подключить к неиспользуемому выходу на выходном коммутаторе, но для этого, возможно, придется перераспределить существующие вызовы, назначив их различным коммутаторам центральной сцены в сети Clos.[5] Чтобы доказать это, достаточно рассмотреть м = п, при полной загрузке сети Clos; то есть, р×п звонки в процессе. Доказательство показывает, как любая перестановка этих р×п входные клеммы на р×п выходные клеммы могут быть разбиты на более мелкие перестановки, каждая из которых может быть реализована отдельными переключающими панелями в сети Clos с м = п.

Доказательство использует Теорема холла о браке[6] которому дано это название, потому что его часто объясняют следующим образом. Предположим, есть р мальчики и р девушки. Теорема утверждает, что если каждое подмножество k мальчики (для каждого k такое, что 0 ≤ k ≤ р) между ними знаю k или больше девочек, то каждый мальчик может быть объединен с девушкой, которую он знает. Очевидно, что это необходимое условие для спаривания; что удивительно, так это то, что этого достаточно.

В контексте сети Clos каждый мальчик представляет входной переключатель, а каждая девочка представляет выходной переключатель. Считается, что мальчик знает девочку, если соответствующие переключатели входа и выхода передают один и тот же вызов. Каждый набор k мальчики должны знать хотя бы k девочки, потому что k входные переключатели несут k×п звонки, и они не могут быть доставлены менее чем k выключатели выхода. Следовательно, каждый входной коммутатор может быть спарен с выходным коммутатором, передающим тот же вызов, посредством взаимно-однозначного сопоставления. Эти р вызовы могут передаваться одним переключателем средней ступени. Если этот переключатель среднего уровня теперь удален из сети Clos, м уменьшается на 1, и мы остаемся с меньшей сетью Клоса. Затем процесс повторяется до тех пор, пока м = 1, и каждый вызов назначается переключателю среднего уровня.

Вероятности блокировки: приближения Ли и Якобея

Реальные системы телефонной коммутации редко бывают неблокируемыми строго по соображениям стоимости, и у них есть небольшая вероятность блокировки, которая может быть оценена специалистами Ли или Якобей приближения,[7] при условии отсутствия перестановок существующих вызовов. Здесь потенциальное количество других активных вызовов на каждом входящем или исходящем коммутаторе равно ты = п−1.

В приближении Ли предполагается, что каждое внутреннее звено между этапами уже занято вызовом с определенной вероятностью п, и что это совершенно независимо между разными ссылками. Это переоценивает вероятность блокировки, особенно для небольших р. Вероятность того, что данная внутренняя ссылка занята, равна п = uq/м, куда q вероятность того, что входящий или выходной канал занят. И наоборот, вероятность того, что ссылка свободна, равна 1−п. Вероятность того, что путь, соединяющий входной коммутатор с выходным коммутатором через конкретный коммутатор среднего уровня, свободен, - это вероятность того, что оба канала свободны, (1−п)2. Следовательно, вероятность его недоступности равна 1− (1−п)2 = 2п−п2. Вероятность блокировки или вероятность того, что ни один из таких путей не свободен, тогда равна [1− (1−п)2]м.

Приближение Якобея более точное, и чтобы увидеть, как оно выводится, предположим, что некое конкретное отображение вызовов, поступающих в сеть Clos (входные вызовы), уже существует на коммутаторах среднего уровня. Это отражает тот факт, что только относительный Конфигурация входного и выходного переключателей имеет значение. Есть я входящие вызовы поступают через тот же входной переключатель, что и подключаемый свободный входной терминал, и j вызовы, покидающие сеть Clos (выходные вызовы) через тот же выходной коммутатор, что и свободный выходной терминал, который должен быть подключен. Следовательно, 0 ≤ я ≤ ты, и 0 ≤ j ≤ ты.

Позволять А быть количеством способов присвоения j выходные вызовы в м переключатели средней ступени. Позволять B быть количеством этих назначений, которые приводят к блокировке. Это количество случаев, когда оставшиеся м−j переключатели средней ступени совпадают с м−j из я входные вызовы, то есть количество подмножеств, содержащих м−j этих звонков. Тогда вероятность блокировки равна:

Если жя вероятность того, что я другие вызовы уже активны на входном коммутаторе, и граммj вероятность того, что j другие вызовы уже активны на исходящем коммутаторе, общая вероятность блокировки составляет:

Это можно оценить с помощью жя и граммj каждый обозначается биномиальное распределение. После значительных алгебраических манипуляций это можно записать как:

Закрытые сети с более чем тремя этапами

Сети Clos также могут быть обобщены на любое нечетное количество этапов. Путем замены каждого перекрестного переключателя центральной сцены на трехступенчатую сеть Clos можно построить пятиступенчатую сеть Clos. Повторное применение одного и того же процесса позволяет получить 7, 9, 11, ... этапов.

Сеть Бенеш (м = п = 2)

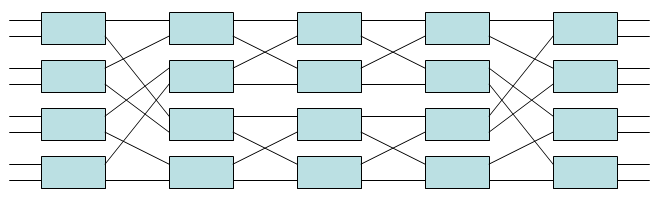
Переставляемая неблокирующая сеть этого типа с м = п = 2 обычно называют Сеть Бенеш, хотя это обсуждалось и анализировалось другими раньше Вацлав Э. Бенеш. Количество входов и выходов N = р×п = 2р. В таких сетях 2 лог2N - 1 этап, каждый из которых содержит N/ 2 перекрестных переключателя 2 × 2 и использовать в общей сложности N бревно2N − N/ 2 перекрестных переключателя 2 × 2. Например, сеть Beneš 8 × 8 (т.е. с N = 8) показано ниже; у него 2 журнала28-1 = 5 ступеней, каждая из которых содержит N/ 2 = 4 перекрестных переключателя 2 × 2, и он использует в общей сложности N бревно2N − N/ 2 = 20 перекрестных переключателей 2 × 2. Три центральных этапа состоят из двух меньших сетей Beneš 4 × 4, в то время как на центральной сцене каждый перекрестный коммутатор 2 × 2 может сам по себе рассматриваться как сеть Beneš 2 × 2. Таким образом, в этом примере подчеркивается рекурсивное построение сети этого типа.

Benesnetwork.png

Смотрите также

Рекомендации

  1. ^ Патент США 2244004 
  2. ^ Кло, Чарльз (март 1953 г.). «Исследование неблокирующих коммутационных сетей». Технический журнал Bell System. 32 (2): 406–424. Дои:10.1002 / j.1538-7305.1953.tb01433.x. ISSN  0005-8580.
  3. ^ Хогг, Скотт (11 января 2014 г.). «Clos Networks: что старое, то снова новое». Сетевой мир.
  4. ^ Мур, Сэмюэл (31 октября 2018 г.). «Flex Logix заявляет, что решила проблему DRAM Deep Learning». Spectrum.ieee.org. IEEE Spectrum. Получено 1 ноября 2018.
  5. ^ Бенеш, Вацлав Э. (11 сентября 1965 г.). Математическая теория объединения сетей и телефонного трафика. Академическая пресса. ISBN  0-12-087550-0.
  6. ^ Холл, Филипп (Январь 1935 г.). «О представителях подмножеств» (PDF). Журнал Лондонского математического общества. s1. 10 (1): 26–30. Дои:10.1112 / jlms / s1-10.37.26. Получено 2015-06-18.
  7. ^ Хуэй, Джозеф Ю. (1990). Теория коммутации и трафика для интегрированных широкополосных сетей. Kluwer Academic. ISBN  0-7923-9061-X.