Цикломатическая сложность - Cyclomatic complexity

Цикломатическая сложность это метрика программного обеспечения используется для обозначения сложность программы. Это количественная мера количества линейно независимых путей через программу исходный код. Он был разработан Томас Дж. МакКейб, старший в 1976 г.

Цикломатическая сложность вычисляется с использованием график потока управления программы: узлы график соответствуют неделимым группам команд программы, а направленный edge соединяет два узла, если вторая команда может быть выполнена сразу после первой команды. Цикломатическая сложность также может применяться к индивидуальным функции, модули, методы или классы в программе.

Один тестирование стратегия, называемая тестирование базового пути Маккейб, который первым предложил это, заключается в проверке каждого линейно независимого пути в программе; в этом случае количество тестовых примеров будет равно цикломатической сложности программы.^[1]

Описание

Определение

График потока управления простой программы. Программа начинает выполнение на красном узле, затем входит в цикл (группа из трех узлов непосредственно под красным узлом). При выходе из цикла появляется условный оператор (группа под циклом), и, наконец, программа завершается в синем узле. У этого графа 9 ребер, 8 узлов и 1 связный компонент, поэтому цикломатическая сложность программы составляет 9-8 + 2 * 1 = 3.

Цикломатическая сложность участка исходный код - количество линейно независимых пути внутри него - где «линейно независимый» означает, что каждый путь имеет по крайней мере одно ребро, которого нет ни в одном из других путей. Например, если исходный код не содержал операторы потока управления (условные выражения или точки принятия решения), сложность будет равна 1, поскольку в коде будет только один путь. Если бы в коде был один оператор IF с одним условием, в коде было бы два пути: один, в котором оператор IF принимает значение TRUE, и другой, где он оценивается как FALSE, поэтому сложность будет равна 2. Два вложенных оператора IF с одним условием , или один IF с двумя условиями, даст сложность 3.

Математически цикломатическая сложность структурированная программа^[а] определяется со ссылкой на график потока управления программы, ориентированный граф содержащий базовые блоки программы с границей между двумя базовыми блоками, если управление может переходить от первого ко второму. Сложность M тогда определяется как^[2]

M = E − N + 2п,

где

E = количество ребер графа.

N = количество узлов графа.

п = количество связанные компоненты.

Та же функция, что и выше, представлена с использованием альтернативной формулировки, в которой каждая точка выхода соединена с точкой входа. Этот граф имеет 10 ребер, 8 узлов и 1 связный компонент, что также приводит к цикломатической сложности 3 при использовании альтернативной формулировки (10-8 + 1 = 3).

Альтернативная формулировка - использовать график, на котором каждая точка выхода связана с точкой входа. В этом случае график сильно связанный, а цикломатическая сложность программы равна цикломатическое число своего графика (также известного как первый номер Бетти ), который определяется как^[2]

M = E − N + п.

Это можно рассматривать как подсчет количества линейно независимые циклы которые существуют в графе, то есть те циклы, которые не содержат внутри себя других циклов. Обратите внимание: поскольку каждая точка выхода возвращается к точке входа, существует по крайней мере один такой цикл для каждой точки выхода.

Для отдельной программы (или подпрограммы, или метода), п всегда равно 1. Таким образом, более простая формула для одной подпрограммы:

M = E − N + 2.^[3]

Однако цикломатическая сложность может применяться к нескольким таким программам или подпрограммам одновременно (например, ко всем методам в классе), и в этих случаях п будет равно количеству рассматриваемых программ, поскольку каждая подпрограмма будет отображаться как несвязанное подмножество графика.

МакКейб показал, что цикломатическая сложность любой структурированной программы только с одной точкой входа и одной точкой выхода равна количеству точек принятия решения (т.е. операторов «если» или условных циклов), содержащихся в этой программе, плюс один. Однако это верно только для точек принятия решения, подсчитываемых на самых нижних командах машинного уровня.^[4] Решения, включающие составные предикаты, подобные тем, которые встречаются в языках высокого уровня, таких как ЕСЛИ cond1 И cond2 ТО ... должны быть подсчитаны с точки зрения задействованных переменных-предикатов, т.е. в этом примере нужно подсчитать две точки принятия решения, потому что на машинном уровне это эквивалентно ЕСЛИ cond1 ТО ЕСЛИ cond2 ТО ....^[2]^[5]

Цикломатическая сложность может быть расширена до программы с несколькими точками выхода; в этом случае он равен

π - s + 2,

где π - количество точек принятия решения в программе, а s - количество точек выхода.^[5]^[6]

Объяснение в терминах алгебраической топологии

An даже подграф графа (также известного как Эйлеров подграф ) это тот, где каждый вершина инцидентно четному числу ребер; такие подграфы представляют собой объединение циклов и изолированных вершин. В дальнейшем четные подграфы будут отождествляться с их наборами ребер, что эквивалентно рассмотрению только тех четных подграфов, которые содержат все вершины полного графа.

Множество всех четных подграфов графа замкнуто относительно симметричная разница, и поэтому его можно рассматривать как векторное пространство над GF (2); это векторное пространство называется велосипедное пространство графа. В цикломатическое число графа определяется как размерность этого пространства. Поскольку GF (2) имеет два элемента и пространство циклов обязательно конечно, цикломатическое число также равно 2-логарифму числа элементов в пространстве циклов.

Основание для пространства цикла легко построить, предварительно установив покрывающий лес графа, а затем рассматривая циклы, образованные одним ребром не в лесу, и тропинкой в лесу, соединяющей концы этого ребра; эти циклы составляют основу пространства цикла. Следовательно, цикломатическое число также равно количеству ребер, не входящих в максимальный остовный лес графа. Поскольку количество ребер в максимальном остовном лесу графа равно количеству вершин минус количество компонентов, формула ${ Displaystyle E-N + P}$ выше для цикломатического числа следует.^[7]

Для более склонных к топологии цикломатическая сложность может быть альтернативно определена как относительная Бетти число, размер относительная гомология группа:

{ Displaystyle M: ​​= b_ {1} (G, t): = operatorname {rank} H_ {1} (G, t),}

который читается как «ранг первой группы гомологий графа г, относительно конечных узлов т". Это технический способ обозначить" количество линейно независимых путей через потоковый граф от входа до выхода ", где:

«линейно независимый» соответствует гомологии и означает, что обратный отсчет не производится дважды;
"пути" соответствует первый гомология: путь - это одномерный объект;
«относительный» означает, что путь должен начинаться и заканчиваться в точке входа или выхода.

Это соответствует интуитивному представлению о цикломатической сложности и может быть рассчитано, как указано выше.

В качестве альтернативы, можно вычислить это через абсолютное число Бетти (абсолютная гомология, а не относительная), идентифицировав (склеив вместе) все конечные узлы на данном компоненте (или, что эквивалентно, нарисовав пути, соединяющие выходы со входом), в этом случае (вызов новый расширенный граф ${ displaystyle { tilde {G}}}$ , который^{[требуется разъяснение ]}), получаем

{ displaystyle M = b_ {1} ({ tilde {G}}) = operatorname {rank} H_ {1} ({ tilde {G}}).}

Его также можно вычислить с помощью гомотопия. Если рассматривать граф потока управления как одномерный CW комплекс называется ${ displaystyle X}$ , то фундаментальная группа из ${ displaystyle X}$ будет ${ displaystyle pi _ {1} (X) = mathbb {Z} ^ {n}}$ . Значение ${ displaystyle n + 1}$ это цикломатическая сложность. Фундаментальная группа считает, сколько петель проходит через граф, вплоть до гомотопии, и, следовательно, согласуется с тем, что мы интуитивно ожидаем.

Это соответствует описанию цикломатической сложности как «количество петель плюс количество компонентов».

Приложения

Ограничение сложности во время разработки

Одно из оригинальных приложений МакКейба заключалось в ограничении сложности процедур во время разработки программы; он рекомендовал программистам подсчитывать сложность разрабатываемых модулей и разбивать их на более мелкие модули всякий раз, когда цикломатическая сложность модуля превышает 10.^[2] Эта практика была принята NIST Методология структурированного тестирования с наблюдением, что с момента первоначальной публикации МакКейба цифра 10 получила существенные подтверждающие доказательства, но что в некоторых обстоятельствах может быть целесообразно ослабить ограничение и разрешить модули со сложностью до 15. Что касается методологии признал, что были случайные причины для выхода за пределы согласованного лимита, он сформулировал свою рекомендацию как «Для каждого модуля либо ограничьте цикломатическую сложность [согласованным пределом], либо предоставьте письменное объяснение того, почему предел был превышен».^[8]

Измерение «структурированности» программы

Раздел VI статьи МакКейба 1976 года посвящен определению того, какие графы управляющих потоков (CFG) не-структурированные программы выглядят с точки зрения их подграфов, которые определяет МакКейб. (Подробнее об этой части см. теорема о структурированной программе МакКейб заключает этот раздел, предлагая численную меру того, насколько близка к идеалу структурированного программирования данная программа, то есть ее «структурированность», используя неологизм МакКейба. Маккейб назвал меру, которую он разработал для этой цели существенная сложность.^[2]

Чтобы вычислить этот показатель, исходный CFG итеративно сокращается путем определения подграфов, которые имеют точку с одним входом и точку с одним выходом, которые затем заменяются одним узлом. Это сокращение соответствует тому, что сделал бы человек, если бы он извлек подпрограмму из большего фрагмента кода. (В наши дни такой процесс подпадал бы под общий термин рефакторинг.) Метод редукции МакКейба позже был назван конденсация в некоторых учебниках, потому что это рассматривалось как обобщение уплотнение к компонентам, используемым в теории графов.^[9] Если программа структурирована, то процесс редукции / уплотнения МакКейба сводит ее к одному узлу CFG. Напротив, если программа не структурирована, итерационный процесс идентифицирует несократимую часть. Существенная мера сложности, определенная МакКейбом, - это просто цикломатическая сложность этого неприводимого графа, поэтому она будет в точности 1 для всех структурированных программ, но больше единицы для неструктурированных программ.^[8]^:80

Последствия для тестирования программного обеспечения

Еще одно применение цикломатической сложности - определение количества тестовых примеров, необходимых для достижения полного тестового покрытия конкретного модуля.

Это полезно из-за двух свойств цикломатической сложности: M, для конкретного модуля:

M - это верхняя граница количества тестовых примеров, необходимых для достижения полного покрытие филиала.
M - это нижняя граница количества путей через граф потока управления (CFG). Предполагая, что каждый тестовый пример проходит по одному пути, количество случаев, необходимых для достижения покрытие пути равно количеству путей, которые реально можно пройти. Но некоторые пути могут быть невозможными, поэтому, хотя количество путей через CFG явно является верхней границей количества тестовых примеров, необходимых для покрытия пути, последнее число (из возможное путей) иногда меньше M.

Все три приведенных выше числа могут быть равны: покрытие филиала ${ displaystyle leq}$ цикломатическая сложность ${ displaystyle leq}$ количество путей.

Например, рассмотрим программу, состоящую из двух последовательных операторов if-then-else.

если (c1())    f1();еще    f2();если (c2())    f3();еще    f4();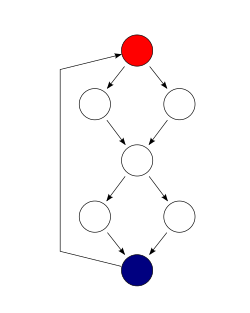

График потока управления исходного кода выше; красный кружок - это точка входа в функцию, а синий кружок - это точка выхода. Выход был соединен со входом, чтобы граф был сильно связан.

В этом примере двух тестовых примеров достаточно для достижения полного покрытия ветки, а четырех необходимо для полного покрытия пути. Цикломатическая сложность программы равна 3 (так как сильно связный граф для программы содержит 9 ребер, 7 узлов и 1 компонент связности) (9-7 + 1).

В общем, для того, чтобы полностью протестировать модуль, должны быть проверены все пути выполнения через модуль. Это означает, что для модуля с большим числом сложности требуется больше усилий по тестированию, чем для модуля с более низким значением, поскольку более высокое число сложности указывает на большее количество путей прохождения кода. Это также означает, что модуль с более высокой сложностью труднее понять программисту, поскольку программист должен понимать различные пути и результаты этих путей.

К сожалению, не всегда практично проверять все возможные пути прохождения программы. Рассматривая приведенный выше пример, каждый раз, когда добавляется дополнительный оператор if-then-else, количество возможных путей увеличивается в 2 раза. По мере роста программы таким образом она быстро достигает точки, когда проверка всех путей становится непрактично.

Одна из распространенных стратегий тестирования, поддерживаемая, например, методология структурированного тестирования NIST, заключается в использовании цикломатической сложности модуля для определения количества тесты белого ящика которые необходимы для получения достаточного покрытия модуля. Почти во всех случаях, согласно такой методологии, модуль должен иметь как минимум столько тестов, сколько его цикломатическая сложность; в большинстве случаев этого количества тестов достаточно для проверки всех соответствующих путей выполнения функции.^[8]

В качестве примера функции, которая требует большего, чем просто покрытие ветвей для точного тестирования, снова рассмотрим приведенную выше функцию, но предположим, что во избежание возникновения ошибки любой код, вызывающий либо f1 (), либо f3 (), должен также вызывать другой.^[b] Предполагая, что результаты c1 () и c2 () независимы, это означает, что функция, представленная выше, содержит ошибку. Покрытие ветвей позволит нам протестировать метод всего двумя тестами, и один из возможных наборов тестов будет тестировать следующие случаи:

c1 () возвращает истину и c2 () возвращает истину
c1 () возвращает false и c2 () возвращает ложь

Ни один из этих случаев не обнаруживает ошибки. Если, однако, мы используем цикломатическую сложность для обозначения количества требуемых тестов, это число увеличивается до 3. Следовательно, мы должны протестировать один из следующих путей:

c1 () возвращает истину и c2 () возвращает ложь
c1 () возвращает false и c2 () возвращает истину

Любой из этих тестов выявит ошибку.

Соотношение количества дефектов

В ряде исследований изучалась корреляция между цикломатическим числом сложности МакКейба и частотой дефектов, возникающих в функции или методе.^[10] Некоторые исследования^[11] найти положительную корреляцию между цикломатической сложностью и дефектами: функции и методы, которые имеют наивысшую сложность, как правило, также содержат наибольшее количество дефектов. Однако корреляция между цикломатической сложностью и размером программы (обычно измеряется в строки кода ) было продемонстрировано много раз. Les Hatton потребовал^[12] эта сложность имеет такую же прогностическую способность, как и строки кода. Исследования, в которых учитывался размер программы (т. е. сравнение модулей, которые имеют разную сложность, но схожий размер), как правило, менее убедительны: многие не обнаруживают значимой корреляции, в то время как другие находят корреляцию. Некоторые исследователи, изучающие эту область, сомневаются в достоверности методов, используемых в исследованиях, не обнаруживая корреляции.^[13] Хотя эта связь, вероятно, верна, ее нелегко использовать.^[14] Поскольку размер программы не является контролируемой функцией коммерческого программного обеспечения, полезность числа МакКейбса была поставлена под сомнение.^[10] Суть этого наблюдения заключается в том, что более крупные программы имеют тенденцию быть более сложными и иметь больше дефектов. Уменьшение цикломатической сложности кода - это не доказано чтобы уменьшить количество ошибок в этом коде. Международные стандарты безопасности, такие как ISO 26262 тем не менее, предписывают руководящие принципы кодирования, которые обеспечивают низкую сложность кода.^[15]

Искусственный интеллект

Цикломатическая сложность также может использоваться для оценки семантической сложности программ искусственного интеллекта.^[16]

Ультраметрическая топология

Цикломатическая сложность оказалась полезной в географическом и ландшафтно-экологическом анализе, после того как было показано, что ее можно реализовать на графиках ультраметрический расстояния.^[17]

Смотрите также

Заметки

^ Здесь «структурированный» означает, в частности, «с одним выходом (заявление о возврате ) на функцию ".
^ Это довольно распространенный тип состояния; рассмотрите возможность того, что f1 выделяет некоторый ресурс, который высвобождает f3.

использованная литература

^ А. Дж. Соби. «Тестирование базового пути».
^ ^а ^б ^c ^d ^е МакКейб (декабрь 1976 г.). «Мера сложности». IEEE Transactions по разработке программного обеспечения (4): 308–320. Дои:10.1109 / цэ.1976.233837.
^ Филип А. Лапланте (25 апреля 2007 г.). Что каждый инженер должен знать о разработке программного обеспечения. CRC Press. п. 176. ISBN 978-1-4200-0674-2.
^ Фрикер, Себастьян (апрель 2018 г.). "Что такое цикломатическая сложность?". froglogic GmbH. Получено 27 октября, 2018. Чтобы вычислить графическое представление кода, мы можем просто дизассемблировать его ассемблерный код и создать граф, следуя правилам: ...
^ ^а ^б Белцер, Кент, Хольцман и Уильямс (1992). Энциклопедия компьютерных наук и технологий. CRC Press. С. 367–368.CS1 maint: несколько имен: список авторов (ссылка на сайт)
^ Харрисон (октябрь 1984 г.). «Применение меры сложности Маккабе к программам с несколькими выходами». Программное обеспечение: практика и опыт. 14 (10): 1004–1007. Дои:10.1002 / spe.4380141009.
^ Дистель, Рейнхард (2000). Теория графов. Тексты для выпускников по математике 173 (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98976-1.
^ ^а ^б ^c Артур Х. Уотсон; Томас Дж. МакКейб (1996). «Структурированное тестирование: методология тестирования с использованием метрики цикломатической сложности» (PDF). Специальная публикация NIST 500-235.
^ Пол К. Йоргенсен (2002). Тестирование программного обеспечения: подход мастера, второе издание (2-е изд.). CRC Press. С. 150–153. ISBN 978-0-8493-0809-3.
^ ^а ^б Норман Э. Фентон; Мартин Нил (1999). «Критика моделей прогнозирования дефектов программного обеспечения» (PDF). IEEE Transactions по разработке программного обеспечения. 25 (3): 675–689. CiteSeerX 10.1.1.548.2998. Дои:10.1109/32.815326.
^ Шредер, Марк (1999). «Практическое руководство по объектно-ориентированным метрикам». ИТ-специалист. 1 (6): 30–36. Дои:10.1109/6294.806902. S2CID 14945518.
^ Лес Хаттон (2008). «Роль эмпиризма в повышении надежности программного обеспечения будущего». версия 1.1.
^ Кан (2003). Метрики и модели в инженерии качества программного обеспечения. Эддисон-Уэсли. С. 316–317. ISBN 978-0-201-72915-3.
^ Г.С.Черф (1992). «Исследование характеристик обслуживания и поддержки коммерческого программного обеспечения». Журнал качества программного обеспечения. 1 (3): 147–158. Дои:10.1007 / bf01720922. ISSN 1573-1367.
^ ISO 26262-3: 2011 (en) Транспорт дорожный - Функциональная безопасность - Часть 3: Фаза концепции. Международная организация по стандартизации.
^ Пападимитриу, Fivos (2012). «Искусственный интеллект в моделировании сложности трансформации средиземноморского ландшафта». Компьютеры и электроника в сельском хозяйстве. 81: 87–96. Дои:10.1016 / j.compag.2011.11.009.
^ Пападимитриу, Fivos (2013). «Математическое моделирование землепользования и ландшафтной сложности с ультраметрической топологией». Журнал науки о землепользовании. 8 (2): 234–254. Дои:10.1080 / 1747423X.2011.637136.

внешние ссылки

[2] Здесь «структурированный» означает, в частности, «с одним выходом (заявление о возврате ) на функцию ".

[11] Это довольно распространенный тип состояния; рассмотрите возможность того, что f1 выделяет некоторый ресурс, который высвобождает f3.

[1] А. Дж. Соби. «Тестирование базового пути».

[mccabe76-3] а ^б ^c ^d ^е МакКейб (декабрь 1976 г.). «Мера сложности». IEEE Transactions по разработке программного обеспечения (4): 308–320. Дои:10.1109 / цэ.1976.233837.

[Laplante2007-4] Филип А. Лапланте (25 апреля 2007 г.). Что каждый инженер должен знать о разработке программного обеспечения. CRC Press. п. 176. ISBN 978-1-4200-0674-2.

[5] Фрикер, Себастьян (апрель 2018 г.). "Что такое цикломатическая сложность?". froglogic GmbH. Получено 27 октября, 2018. Чтобы вычислить графическое представление кода, мы можем просто дизассемблировать его ассемблерный код и создать граф, следуя правилам: ...

[ecst-6] а ^б Белцер, Кент, Хольцман и Уильямс (1992). Энциклопедия компьютерных наук и технологий. CRC Press. С. 367–368.CS1 maint: несколько имен: список авторов (ссылка на сайт)

[harrison-7] Харрисон (октябрь 1984 г.). «Применение меры сложности Маккабе к программам с несколькими выходами». Программное обеспечение: практика и опыт. 14 (10): 1004–1007. Дои:10.1002 / spe.4380141009.

[8] Дистель, Рейнхард (2000). Теория графов. Тексты для выпускников по математике 173 (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98976-1.

[nist-9] а ^б ^c Артур Х. Уотсон; Томас Дж. МакКейб (1996). «Структурированное тестирование: методология тестирования с использованием метрики цикломатической сложности» (PDF). Специальная публикация NIST 500-235.

[10] Пол К. Йоргенсен (2002). Тестирование программного обеспечения: подход мастера, второе издание (2-е изд.). CRC Press. С. 150–153. ISBN 978-0-8493-0809-3.

[fenton-12] а ^б Норман Э. Фентон; Мартин Нил (1999). «Критика моделей прогнозирования дефектов программного обеспечения» (PDF). IEEE Transactions по разработке программного обеспечения. 25 (3): 675–689. CiteSeerX 10.1.1.548.2998. Дои:10.1109/32.815326.

[schroeder99-13] Шредер, Марк (1999). «Практическое руководство по объектно-ориентированным метрикам». ИТ-специалист. 1 (6): 30–36. Дои:10.1109/6294.806902. S2CID 14945518.

[taic-14] Лес Хаттон (2008). «Роль эмпиризма в повышении надежности программного обеспечения будущего». версия 1.1.

[kan-15] Кан (2003). Метрики и модели в инженерии качества программного обеспечения. Эддисон-Уэсли. С. 316–317. ISBN 978-0-201-72915-3.

[cherf-16] Г.С.Черф (1992). «Исследование характеристик обслуживания и поддержки коммерческого программного обеспечения». Журнал качества программного обеспечения. 1 (3): 147–158. Дои:10.1007 / bf01720922. ISSN 1573-1367.

[ISO26262Part3-17] ISO 26262-3: 2011 (en) Транспорт дорожный - Функциональная безопасность - Часть 3: Фаза концепции. Международная организация по стандартизации.

[18] Пападимитриу, Fivos (2012). «Искусственный интеллект в моделировании сложности трансформации средиземноморского ландшафта». Компьютеры и электроника в сельском хозяйстве. 81: 87–96. Дои:10.1016 / j.compag.2011.11.009.

[19] Пападимитриу, Fivos (2013). «Математическое моделирование землепользования и ландшафтной сложности с ультраметрической топологией». Журнал науки о землепользовании. 8 (2): 234–254. Дои:10.1080 / 1747423X.2011.637136.

[1]

[а]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[b]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]