Напряжение цилиндра - Cylinder stress

В механика, а напряжение цилиндра это стресс распределение с вращательной симметрией; то есть, который остается неизменным, если объект, находящийся под напряжением, вращается вокруг некоторой фиксированной оси.
Модели напряжений в цилиндрах включают:
- окружное напряжение, или же растягивающая нагрузка центробежного происхождения, нормальное напряжение в касательной (азимут ) направление.
- осевое напряжение- нормальное напряжение, параллельное оси цилиндрической симметрии.
- радиальное напряжение- нормальное напряжение в направлениях, копланарных, но перпендикулярных оси симметрии.
Эти три главных напряжения - кольцевое, продольное и радиальное - могут быть рассчитаны аналитически с использованием взаимно перпендикулярной трехосной системы напряжений.[1]
Классический пример (и тезка) обручального стресса - это напряжение наносится на железные ленты или обручи деревянного бочка. По прямой, закрытой трубка, любая сила, приложенная к стенке цилиндрической трубы давление дифференциал в конечном итоге вызовет кольцевые напряжения. Точно так же, если эта труба имеет плоские торцевые заглушки, любая сила, приложенная к ним статическим давлением, вызовет перпендикулярный осевое напряжение на той же стенке трубы. Тонкие участки часто имеют ничтожно малые размеры. радиальное напряжение, но точные модели толстостенных цилиндрических оболочек требуют учета таких напряжений.
В толстостенных сосудах высокого давления можно использовать методы строительства, позволяющие создавать благоприятные исходные образцы напряжений. Эти сжимающие напряжения на внутренней поверхности уменьшают общее кольцевое напряжение в цилиндрах под давлением. Цилиндрические сосуды такого типа обычно конструируются из концентрических цилиндров, сжатых (или расширяемых) один над другим, т. Е. Составных цилиндров с горячей посадкой, но также могут быть выполнены для отдельных цилиндров посредством автоматического растяжения толстых цилиндров.[2]
Определения
Растягивающая нагрузка центробежного происхождения
Обручальное напряжение - это сила действует по окружности (перпендикулярно оси и радиусу объекта) в обоих направлениях на каждую частицу в стенке цилиндра. Его можно описать как:
куда:
- F это сила приложенный по окружности к области стенки цилиндра, которая имеет две следующие длины в качестве сторон:
- т радиальная толщина цилиндра
- л - осевая длина цилиндра.
Альтернатива растягивающая нагрузка центробежного происхождения при описании окружного напряжения напряжение стены или же натяжение стены (Т), которая обычно определяется как полная окружная сила, действующая по всей радиальной толщине:[3]
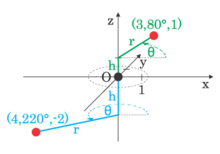
Наряду с осевым напряжением и радиальное напряжение, окружное напряжение является составляющей тензор напряжений в цилиндрическом координаты.
Обычно полезно разлагать любая сила, приложенная к объекту с вращательная симметрия на компоненты, параллельные цилиндрическим координатам р, z, и θ. Эти компоненты силы вызывают соответствующие напряжения: радиальное напряжение, осевое напряжение и кольцевое напряжение соответственно.
Отношение к внутреннему давлению
Тонкостенное предположение
Чтобы предположение о тонкостенных стенках было верным, сосуд должен иметь толщину стенки не более одной десятой (часто обозначаемой как Диаметр / t> 20) его радиуса.[4] Это позволяет рассматривать стену как поверхность, а затем использовать Уравнение Юнга – Лапласа для оценки кольцевого напряжения, создаваемого внутренним давлением на тонкостенный цилиндрический сосуд высокого давления:
- (для баллона)
- (для шара)
куда
- п это внутреннее давление
- т толщина стенки
- р - средний радиус цилиндра
- это напряжение обруча.
Уравнение кольцевого напряжения для тонких оболочек также приблизительно справедливо для сферических сосудов, включая клетки растений и бактерии, в которых внутренняя тургорное давление может достигать нескольких атмосфер. В практических инженерных приложениях для цилиндров (труб и трубок) кольцевое напряжение часто перераспределяется по давлению и называется Формула Барлоу.
Система дюйм-фунт-секунда (IPS) для п находятся фунт-сила на квадратный дюйм (фунт / кв. дюйм). Единицы для т, и d дюймы (дюймы). п находятся паскали (Па), а т и d=2р указаны в метрах (м).
Когда сосуд закрывается, внутреннее давление действует на них, создавая силу, действующую вдоль оси цилиндра. Это называется осевым напряжением и обычно меньше кольцевого напряжения.
Хотя это может быть приблизительно
Также существует радиальное напряжение которая развернута перпендикулярно поверхности и может быть оценена в тонкостенных цилиндрах как:
Однако в предположении тонкостенного отношения большой, поэтому в большинстве случаев этот компонент считается незначительным по сравнению с кольцевыми и осевыми напряжениями. [5]
Толстостенные сосуды
Когда исследуемый цилиндр имеет отношение менее 10 (часто цитируется как ) уравнения тонкостенного цилиндра больше не выполняются, поскольку напряжения значительно различаются между внутренней и внешней поверхностями и напряжение сдвига через поперечное сечение уже нельзя пренебрегать.
Эти напряжения и деформации можно рассчитать с помощью Уравнения Ламе, система уравнений, разработанная французским математиком Габриэль Ламе.
куда:
- и - константы интегрирования, которые могут быть обнаружены из граничных условий
- радиус в интересующей точке (например, на внутренней или внешней стенах)
и может быть найден путем проверки граничных условий. Например, самый простой случай - цельный цилиндр:
если тогда а твердый цилиндр не может иметь внутреннего давления, поэтому
Как и для толстостенных цилиндров, соотношение больше 10, и, следовательно, радиальным напряжением нельзя пренебречь, заметная толщина стенки становится основным фактором, учитываемым при проектировании (Harvey, 1974, стр. 57).
В теории сосудов высокого давления любой заданный элемент стенки оценивается в системе трехосных напряжений с тремя главными напряжениями: кольцевыми, продольными и радиальными. Следовательно, по определению не существует касательных напряжений в поперечной, касательной или радиальной плоскостях.[6]
В толстостенных цилиндрах максимальное напряжение сдвига в любой точке определяется половиной алгебраической разности между максимальным и минимальным напряжениями, которая, следовательно, равна половине разницы между кольцевым и радиальным напряжениями. Напряжение сдвига достигает максимума на внутренней поверхности, что важно, поскольку оно служит критерием отказа, поскольку хорошо коррелирует с фактическими испытаниями на разрыв толстых цилиндров (Harvey, 1974, стр. 57).
Практические эффекты
Инженерное дело
Разрушение определяется кольцевым напряжением в отсутствие других внешних нагрузок, поскольку это наибольшее главное напряжение. Обратите внимание, что обруч испытывает наибольшую нагрузку внутри (внешняя и внутренняя стороны испытывают одинаковую общую нагрузку, которая распределяется по разным окружностям); следовательно, трещины в трубах теоретически должны начинаться с внутри труба. Вот почему осмотр труб после землетрясений обычно включает отправку камеры внутрь трубы для проверки на наличие трещин. Податливость регулируется эквивалентным напряжением, которое включает кольцевое напряжение и продольное или радиальное напряжение, если оно отсутствует.
Лекарство
в патология из сосудистый или же стенки желудочно-кишечного тракта, натяжение стенки представляет собой мышечное напряжение на стенке сосуда. В результате Закон Лапласа, если аневризма образуется в стенке кровеносного сосуда, увеличился радиус сосуда. Это означает, что внутренняя сила, действующая на сосуд, уменьшается, и поэтому аневризма будет продолжать расширяться, пока не разорвется. Аналогичная логика применима к формированию дивертикулы в кишка.[7]
Историческое развитие теории

Первый теоретический анализ напряжения в цилиндрах был разработан инженером середины 19 века. Уильям Фэйрбэрн, которому помогает его математический аналитик Итон Ходжкинсон. Их первым интересом было изучение дизайна и неудачи из паровые котлы.[9] Фэйрберн понял, что кольцевое напряжение вдвое превышает продольное напряжение, что является важным фактором при сборке кожухов котла из катаных листов, соединенных между собой. захватывающий. Позже работа была применена к строительству мостов и изобретению коробчатая балка. в Железнодорожный мост Чепстоу, то чугун столбы усилены внешними лентами из кованое железо. Вертикальная продольная сила - это сжимающая сила, которой чугун хорошо сопротивляется. Кольцевая нагрузка является растягивающей, поэтому добавляется кованое железо, материал с большей прочностью на разрыв, чем чугун.
Смотрите также
- Может быть вызвано напряжением цилиндра:
- Связанные инженерные темы:
- Дизайн очень сильно пострадал от этого стресса:
Рекомендации
- ^ «Расширенный структурный анализ». Университет Суонси, 2020, https://engweb.swan.ac.uk/~c.kadapa/teaching/2017-2018/EGF316/week2/EGF316%20Thin%20and%20Thick%20Cylinders%20-%20notes.pdf. По состоянию на 23 октября 2020 г., с. 8.
- ^ Харви, Джон Ф. Теория и конструкция современных сосудов под давлением. Ван Ностранд Рейнхольд, 1974, стр.60, 61.
- ^ Напряжение в стенках артерий Автор: R Nave. Кафедра физики и астрономии Государственного университета Джорджии. Проверено июнь 2011 г.
- ^ http://www.engineersedge.com/material_science/hoop-stress.htm
- ^ "Сосуды под давлением" (PDF). web.mit.edu. Получено 2020-06-12.
- ^ «Расширенный структурный анализ». Университет Суонси, 2020, https://engweb.swan.ac.uk/~c.kadapa/teaching/2017-2018/EGF316/week2/EGF316%20Thin%20and%20Thick%20Cylinders%20-%20notes.pdf. По состоянию на 23 октября 2020 г., с. 8.
- ^ Э. Гольян, Патология, 2-е изд. Мосби Эльзевьер, Серия быстрых обзоров.
- ^ Джонс, Стивен К. (2009). Брюнель в Южном Уэльсе. II: Связь и уголь. Страуд: История Press. п. 247. ISBN 9780752449128.
- ^ Fairbairn, Уильям (1851). «Строительство котлов». Две лекции: «Строительство котлов» и «О взрывах котлов со средствами предотвращения».. п. 6.
- Сосуды под давлением с тонкими стенками. Основы инженерии. 19 июня 2008 г.
Эта статья нужны дополнительные цитаты для проверка. (Март 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |




















